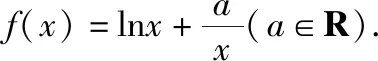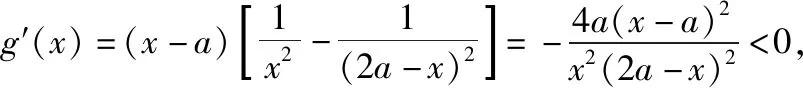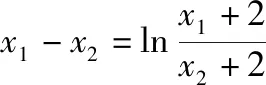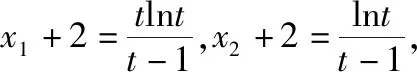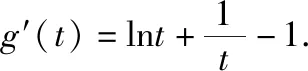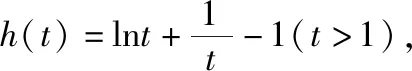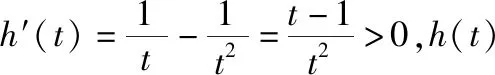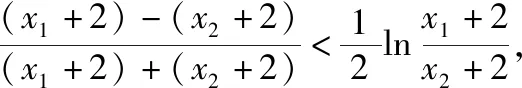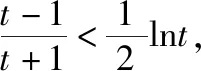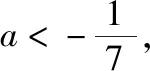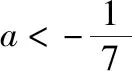利用导数证明不等式的策略
江苏 张连军
2021年高考落下了帷幕,在备受瞩目的新高考Ⅰ卷数学试题中,笔者又发现了久违的老面孔,函数不等式证明问题,这类不等式证明往往需要借助研究函数的性质,结合图形分析推理,而导数是研究函数性质的重要工具,所以这类问题的证明需要通过导数去研究函数,进而推导不等式.作为高考压轴题,思维能力要求高,逻辑关系复杂,往往成为许多学生的痛点.本文就常见的函数不等式证明方法进行简要概述.
一、一元不等式的证明问题
所谓一元不等式,即问题中只有单个变量的不等式证明,常有如下的解题策略:
策略1:作差(商)比较,顺其自然
对于函数不等式证明,最常规的思路就是进行作差(商)比较,构造差(商)值函数,利用函数的最值(值域)证明.

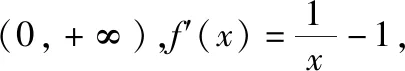
而右边不等式可作差转化为xlnx-x+1>0,
设F(x)=xlnx-x+1,则F′(x)=lnx,
当x>1时,F′(x)>0,所以F(x)在(1,+∞)上单调递增,所以F(x)>F(1)=0,故原不等式得证.此题通过作差法构造函数,利用导数研究函数的单调性与范围,进而证得不等式,是不等式证明的常规解法.
【例2】证明:当x>0时,x2 【点拨】①欲证函数不等式f(x)>g(x),只需证明f(x)-g(x)>0,可设h(x)=f(x)-g(x),即证h(x)>0,亦证h(x)min>0,而这用导数往往容易解决. 策略2:一分为二,柳暗花明 若直接求导比较复杂或无从下手时,可将待证式子进行变形,构造两个都便于求导的函数,从而找到可以传递的中间量,达到证明的目标. 【解析】此题若直接作差(商),很难求得差(商)值函数的最值(值域),原因是合并后的函数结构形式复杂,统一化处理困难,此时可以采用一分为二的策略,将其转化为两个结构较为简单的函数来处理. 易知g(x)在(0,1)上单调递减,在(1,2]上单调递增,故当0 策略3:合理放缩,化繁为简 对于较为复杂的超越不等式,进行适当放缩,可以构造更为简单的函数,事半功倍,以例3第二问为例,可以进行放缩后再构造,使得问题简化.具体如下: 因为当0 因为0 对于跨阶函数的放缩,常见的有指、对数函数与一次函数的放缩,如ex≥x+1,lnx≤x-1等,若能对问题的形式进行合理放缩,使超越函数转化为常见函数,则能起到化繁为简的功效. 策略4:同形构造,研究整体 对于复杂函数中的不同因式,如果能进行相同化的构造,则可以使得构造函数的目标更明确,思维更清晰. 【解析】此题可以采用策略2的方法转化为两个函数, 则原不等式等价于g(lnx)+g(-x)>0, 因为g′(x)=ex(x+1),显然当x=-1时,g(x)有最小值g(-1)=0故g(x)≥0,而g(lnx),g(-x)不能同时为0,故g(lnx)+g(-x)>0,所以不等式成立. 【小结】对复杂函数构造同构函数能使得问题的结构形式更加清晰,更容易从整体把握函数的性质. 所谓多元不等式,即问题中出现两个或两个以上的变量,往往以二元不等式为主,解决多元问题的关键是如何减元,多元化为一元,常有以下策略: 策略1:代入消元,简单明了 (1)求f(x)的最小值; (2)若方程f(x)=0有两个根x1,x2(x1 【解析】(1)当a≤0时,f(x)在(0,+∞)上单调递增,函数无最小值.当a>0时,f(x)最小值为f(a)=lna+1. (2)若函数y=f(x)的两个零点为x1,x2(x1 设0 令g(x)=f(x)-f(2a-x)(0 所以g(x)在(0,a)上单调递减,g(x)>g(a)=0, 即f(x)>f(2a-x). 令x=x1 所以f(x2)=f(x1)>f(2a-x1), 由(1)可得f(x)在(a,+∞)上单调递增,所以x2>2a-x1,故x1+x2>2a. 本题利用f(x1)=f(x2)代入消元,采用分析法构造函数g(x)=f(x)-f(2a-x)(0 策略2:整体换元,思路清晰 【例6】函数f(x)=ex+1-kx-2k.(其中e是自然对数的底数,k∈R) (1)讨论函数f(x)的单调性; (2)若函数y=f(x)的两个零点为x1,x2.证明:x1+x2>-2. 【解析】(1)当k>0时,函数f(x)在(-∞,lnk-1)上单调递减,在(lnk-1,+∞)上单调递增. 当k≤0时,函数f(x)在R上单调递增. (2)当k≤0时,由(1)知函数f(x)在R上单调递增,不存在两个零点,所以k>0, 由题意知ex1+1=k(x1+2),ex2+1=k(x2+2), 欲证x1+x2>-2, 即证(t+1)lnt-2(t-1)>0, 设g(t)=(t+1)lnt-2(t-1)(t>1), 所以g′(t)>g′(1)=0, 故g(t)在区间(1,+∞)上单调递增. 所以g(t)>g(1)=0, 即(t+1)lnt-2(t-1)>0, 所以原不等式得证,故x1+x2>-2. 本题主要利用整体换元的方法,将两个变量用同一字母表示,进而构造函数得解. 策略3:齐次构造,整体并元 对于上题的证明过程还可以通过构造齐次分式来证明: 要证明x1+x2>-2, 即证(x1+2)+(x2+2)>2, 策略4:主次分明,先易后难 【解析】f(x)=(ax2+2ax+1)ex-2=a(x2+2x)ex+ex-2, 令φ(a)=a(x2+2x)ex+ex-2, 显然当x≥0时,(x2+2x)ex≥0, 故要证当x≥0时,f(x)<0, 即证当x≥0时,ex(x2+2x-7)+14>0, 令g(x)=ex(x2+2x-7)+14, 则g′(x)=(x-1)(x+5)ex, 易得g(x)min=g(1)=14-4e>0, 故g(x)>0,从而命题得证. 此题采用分主次元的办法,先从变量a入手,转化为关于a的一次函数,得到关于x的不等式,再利用导数研究关于x的函数,逐个突破,从易到难,把复杂函数转化为常见函数,使之得证.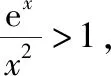
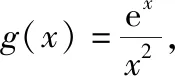



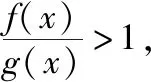


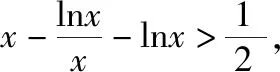
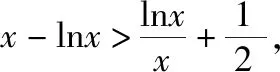
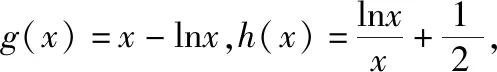
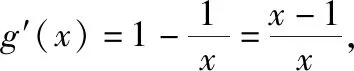

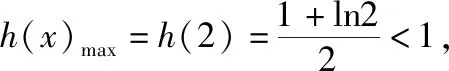

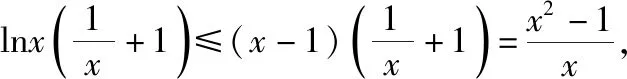



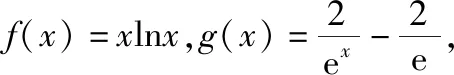
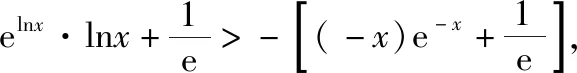
二、多元不等式的证明问题