一题一课落素养 深度教学显神通——一类二元二次型条件下函数最值问题的解法探究

甘肃 张 科 朱军平

随着《普通高中数学课程标准(2017年版2020年修订)》颁布，落实数学学科核心素养愈发为教师所重视，但在实践层面上还需要更有效的探索，笔者在教学实践中基于数学学科核心素养开展深度教学研究.二次型条件下的最值问题是高中数学的热点和难点问题，各类数学考试、高校自主招生和数学竞赛都会涉及二元二次条件下的最值问题，通常可用换元法进行求解，用三角替换或是整体替换，怎样换元，这是学生求解过程中的难点！如何让学生能够“以不变应万变”解答问题，并形成数学学习的技能？本文在高等数学观点下，利用拉格朗日乘数法在二次条件下，对函数z=f(x，y)的最值进行了规范解答与推广应用，有利于高效解决此类问题.

1.试题呈现与解法探究

【试题再现】已知实数x，y满足5x2-y2-4xy=5，则2x2+y2的最小值是

( )

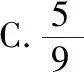
【命题意图】本题是一道二次型条件下的最值问题，意在考查学生对二次型最值问题的基本解题思路与消元的解题策略掌握情况.

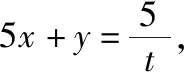
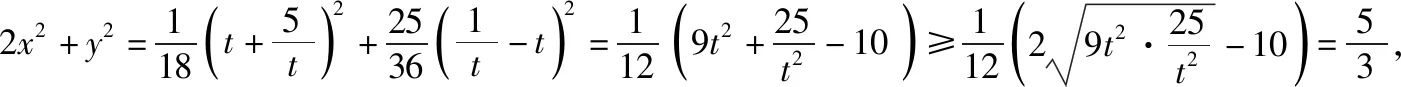
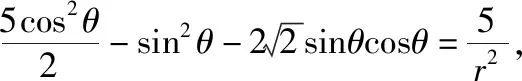
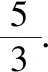
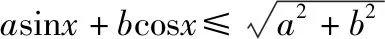
“换元法”是高中阶段学生常用的解决此类问题的方法，但是这种方法操作起来并不容易，那么除了“换元法”之外，是否还有其它方法可以解决此类问题?

如果将此问题从二元函数的角度去分析，会发现此类问题的高等数学背景和本质，其实就是多元函数条件极值、最值问题.令f(x，y)=2x2+y2，φ(x，y)=5x2-y2-4xy-5，则原问题可转化为在条件φ(x，y)=0下，求函数z=f(x，y)的最小值.下面介绍“拉格朗日乘数法”，一种利用高等数学知识求解二元二次代数式的最值的方法.

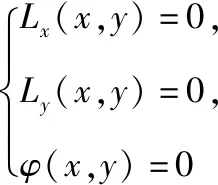
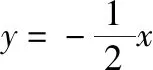
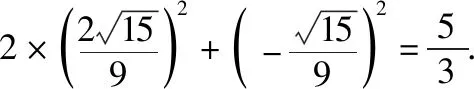
由于上述解法三与前述换元法比较，更加简便、高效，且具有“以不变应万变”的解题功能，所以在高中阶段把这一方法介绍给学生，特别是尖子生是可行的，也是值得推广的.

2.变式探究

变式一：已知x>0，y>0，x+2y+2xy=8，则x+2y的最小值为

( )

A.3 B.4

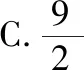
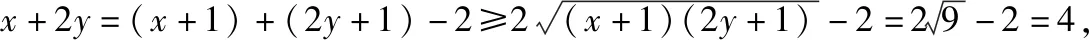
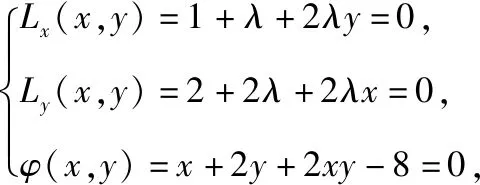
变式二：若正实数x，y满足2x+y+6=xy，则xy的最小值为________.

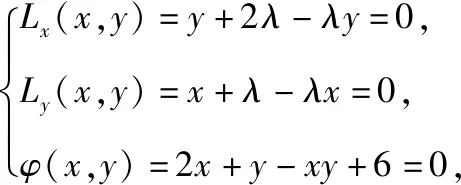
评析：以上两道变式题，利用常规解法具有较强的技巧性，其中变式一对变形能力要求较高，变式二关键在于构建不等式；而创新解法中，只需要按部就班地运用“拉格朗日乘数法”即可顺利获解.

3.考题链接

题1.若正数x，y满足x+3y=5xy，则3x+4y的最小值是

( )

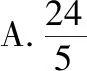
C.5 D.6

题2.实数x，y满足2x2+3y2=6y，则x+y的最大值是________.

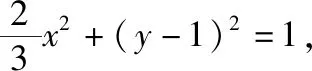
评析：以上两道考题，利用常规解法求解时需要明确解题方向，其中题1灵活借用了“1”的特性和基本不等式，题2灵活运用了三角换元和相关三角函数知识；而创新解法中，只需要按部就班地运用“拉格朗日乘数法”即可顺利获解.

4.推广引申

这类问题在圆锥曲线(椭圆、双曲线、抛物线)中也比较常见，现将此类问题引申到圆锥曲线类似的最值问题中.

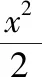
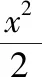
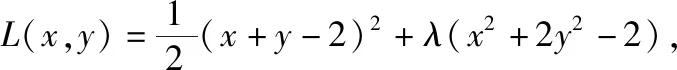
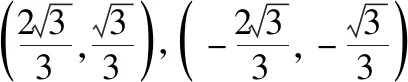
【例2】双曲线x2-4y2=4(x≥2)上是否存在一点到直线y=3x的最短距离，若存在，求出该点坐标；若不存在，请说明理由.

解析：双曲线x2-4y2=4(x≥2)上存在一点到直线y=3x的距离最短，理由如下：

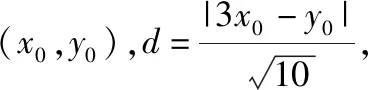
【例3】在抛物线y2=4x上求一点，使得其到直线x+y+4=0的距离最小.

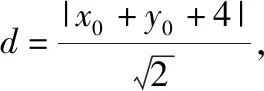
评析：一般地，处理椭圆、双曲线、抛物线上的动点到一条定直线的距离的最值问题，均可灵活运用本文介绍的“拉格朗日乘数法”加以求解.

5.反思感悟

综上，在二元二次型条件下，利用“拉格朗日乘数法”可顺利求解目标函数z=f(x，y)的最值问题.具体解题时，需要先构建构造拉格朗日函数L(x，y)=f(x，y)+λφ(x，y)，其中附加条件为φ(x，y)=0；再通过求导构建方程组，然后解方程组即得最值情境，进而破解目标问题.

在今后的高考复习备考中我们要善于通过一题多解的形式，探究发现具有一般性的解法，即解题通法，其优点是解题步骤程序化，极易操作，从而便于迅速解决问题.