从一道几何光学题的探究过程看科学思维的妙用
湖北 徐爱梅
对物理问题的探究过程,常常需要巧妙地运用科学思维,利用模型建构、科学推理、科学论证、质疑与创新,化复杂为简单,化陌生为熟悉,探寻其本质规律。教师在教学过程中不能只满足于物理问题的解答,应该在问题的解决过程中让学生体会科学思维运用的巧妙,培养学生的科学思维。对于光学试题也是如此。
在笔者印象中,光是自然界最聪明的物质,它总是倾向于更高的效率,比如光总是走最快的路径。我们可以运用类比思维,从光的反射、折射规律中找到求解宏观物体最短运动时间的方法,相较于使用费时的数学方法推导运动规律,运用类比思维的好处是可以根据条件和规律的相似性快速找到解决问题的方法。比如在沙滩上看到一个人落水了,施救者走什么路线可最快到达落水者身边?类比思维的解法是按照施救者在沙滩和水中速度,类比光的折射路径。再如力学上的最速降线问题,也可用光的折射规律来理解,其路径类似于海市蜃楼的光路。
光的折射引起色散时,比较介质中不同色光的传播时间,就要用到比较思维。比较思维能力是物理试题中经常考查的科学思维,比较的时候要善于抓住相同点、联系量、不变量,可以使比较的过程变得更简单。
模型思维能力也是物理创新试题中经常考查的科学思维,常在典型模型的基础上加以变通或组合,考查学生对基本原理或者基本模型的组合运用等。教材上常见的模型有平行玻璃砖、半圆形玻璃砖、三棱镜、全反射棱镜等。《普通高中物理课程标准(2017年版2020年修订)》中特别强调了物理学科核心素养中模型建构的科学思维。一些优秀的模拟题充分体现了这一特点。2021年武昌五月质量检测试卷第9题就是一道考查科学思维的好题。
【试题呈现】某玻璃砖的横截面是底角为45°的等腰梯形,如图1,一束由红绿两色组成的复色光从AB边中点E平行于BC边射入后,两种色光在BC边均发生全反射后再从CD边射出玻璃砖,其中红光的射出点是CD边中点F。除了全反射,不考虑光在玻璃砖内的多次反射,则下列说法正确的是
( )

图1
A.绿光在CD边的出射点在F点下方
B.绿光在CD边出射的方向与BC平行
C.绿光在玻璃砖内传播的时间一定比红光要长
D.绿光在玻璃砖内传播的时间可能和红光相等
一、利用对称性化折线为直线

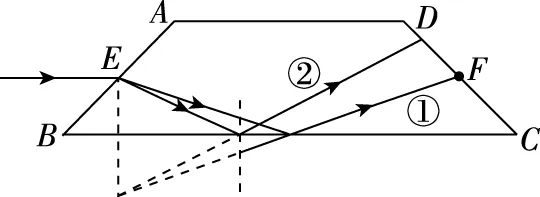
图2
对于一道选择题,命题人应该不是要学生去做复杂的计算,那命题人是不是想普及什么特殊模型的特殊规律呢?笔者联想到课本中曾有一个缝纫机缠线的滚轮从较光滑的桌面斜滚到布面上的情境,因为滚轮的速度大小发生变化导致滚动方向也随之改变,可以帮助理解光的折射现象,其中用到了时间相等来证明折射定律。笔者相信这道模拟题中也一定会存在一个蕴含简单规律的特殊模型。笔者把这个问题抛到一个物理教师QQ群中,并引起各地物理教师的热烈讨论。
二、利用熟悉模型推导结论
安徽省池州市的黎杨老师说:“当做平行玻璃砖问题?折射率大的时间一定大。”
平行玻璃砖是学生比较熟悉的光学元件。但大多数学生只是重点研究过出射光与入射光平行的证明和比较不同折射率的单色光侧移量的大小这两个问题,对比较时间的问题没有深入的研究。如图3所示(①为红光,②为绿光),与笔者作入射光的对称线(作入射点的像点)不同的是,其他几位老师做的是反射光的对称线,相当于做的是出射点的像点,入射点本来就相同,而出射点的像点连线就构成了出射面CD的镜面对称像,很容易发现与平行玻璃砖的联系。
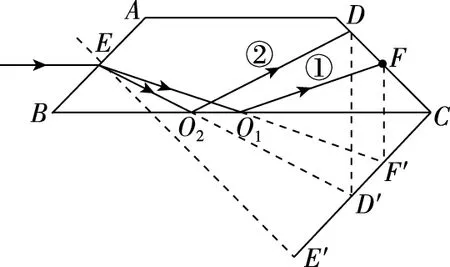
图3
作DC的垂线CE′,EE′⊥CE′,其中E′为垂足,则F、D关于BC面的像点F′、D′也在这条线上。根据对称性,光的路程分别为EF′、ED′。
湖北省武汉市的张旭老师给了这个模型的推导过程与笔者下面的推导类似。
设入射角为i,折射角为θ,平行玻璃砖厚度为d,

结论:入射角i相同,折射角为θ=45°时,当分母有最大值,时间t最短。
讨论:折射率n越大,折射角θ越小。
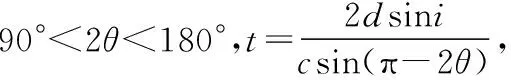

此题入射角等于45°,折射角θ<45°,折射率更大的绿光在等腰梯形玻璃中的传播时间一定比红光长。不过,笔者感觉这种方法的计算量还是有些大,如果学生事先不知道这个模型,考场上推导还是会花费大量时间。作为选择题,还有没有更简洁的模型来解决呢?命题者心中想的是什么模型呢?
三、提出特殊模型速解问题
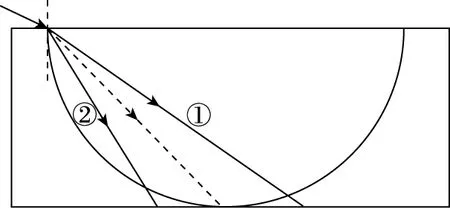
四川省的林斌老师提出:“做个圆直接秒(杀)”。如图4所示(①为红光,②为绿光),红光与绿光同时到达图中圆弧,易得红光的传播时间小于绿光的传播时间。

图4
证明:如图5所示,设圆的直径为2R,入射角为θ,折射角为α,则

图5


由于两种单色光的入射角相等,所以它们经过相同的时间到达圆弧面。
湖北省武汉市的姜付锦老师告诉笔者,这个模型叫惠更斯等时圆:两束不同折射率的单色光以相同的入射角从一半圆形的玻璃砖的左端点入射,则两束单色光在玻璃砖中传播的时间相等。惠更斯等时圆为什么有如此简洁奇妙的特点呢?是否包含什么本质规律?河南省的李亚坤老师说了一句:“同一波面,时间必定相等。介质中换算真空光程。”这就是惠更斯原理的波阵面。
结合等时圆的证明,我们可看出,以相同的入射角射到某一界面的复色光进入介质色散后波到达的点构成的面应该在一个圆面上,圆面的直径在入射面上,入射点为直径的一个端点,随着时间延长,这个直径越来越大。

笔者再一次惊叹于物理规律的相似性,电场、引力场、光学、力学,总能在不同的领域发现相似的规律。静电透镜、引力透镜、磁聚焦与磁发散、光学透镜、磁感线与电场线;运动时间最短问题与费马定律;神奇的三分之二现象;力学和电磁学动态分析中的最终稳态问题;变压器和稳恒电路中的动态分析问题;力学等时圆、光学等时圆……
四、拓展
在解决了之前笔者提出的问题后,湖北省的赵宗坤老师和姜付锦老师又分别给出了两种不同情况的玻璃砖色散问题。

( )
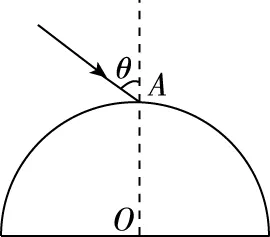
图6
A.t1>t2B.t1=t2C.t1 如图7所示,运用之前得出的结论易得t1>t2,A选项正确。 图7 【例2】频率不同的两束单色光1和2以相同的入射角从同一点射入某种介质后,其光路图如图8所示,下列关于两束光的说法中正确的是 ( ) 图8 A.单色光1比单色光2更容易发生衍射现象 B.单色光1比单色光2更容易发生光电效应现象 C.单色光1与单色光2在介质中的传播时间可能相等 D.单色光1发生全反射的临界角比单色光2的要大 如果熟悉惠更斯等时圆的模型,也可画图速解。如图9所示,折射角为45°时,时间最短。若①②的折射角互余,则时间相等。 图9

五、总结


