第31届全国中学生物理竞赛预赛第11题的几种解法

第31届全国中学生物理竞赛预赛第11题的几种解法

王隆洋

(宁波外国语学校 浙江 宁波315121)

收稿日期：(2014-09-16)

【题目】如图1所示，一水平放置的厚度为t，折射率为n的平行玻璃砖，下表面镀银(成反射镜)．一物点A位于玻璃砖的上方距玻璃砖的上表面为h处．观察者在A点附近看到了A点的像，A点的像到A点的距离等于多少？不考虑光经玻璃砖上表面的反射.

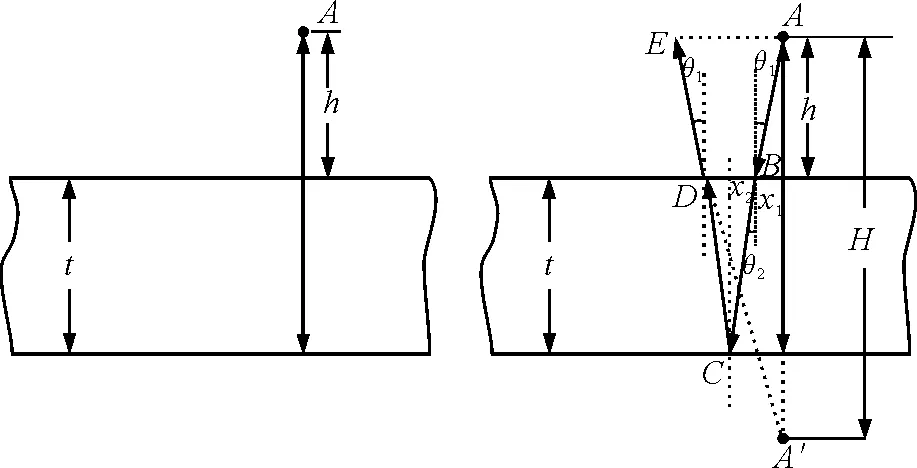
图1 图2

解法1(阅卷参考解答)：如图2所示，由折射定律得

sinθ1=nsinθ2

由几何关系得

x1=htanθ1

x2=ttanθ2

H=2(x1+x2)tan(90°-θ1)

式中H为物A到像A′的距离，在小角度的近似下有

tanθ1≈sinθ1tanθ2≈sinθ2

由以上各式得

解法2(作图法):如图3所示,利用逐次成像法作出物A最终成的像.第一次成像，物A经过玻璃砖上表面折射后，像点为A′，第二次成像是经过玻璃砖下表面反射成像， 所成的像点为A″，第三次成像是经过玻璃砖上表面折射成像，像点A‴即为A最终成的像.

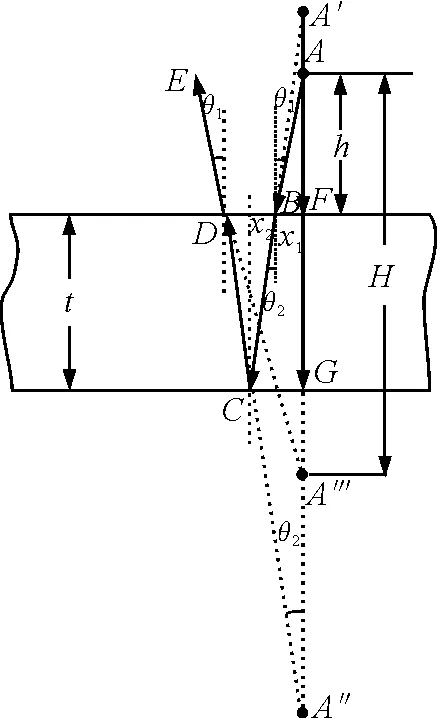
图3

由折射定律得

sinθ1=nsinθ2

在小角度的近似下有

tanθ1≈sinθ1tanθ2≈sinθ2

根据几何知识易得

A′F=nAF=nh

△A′CA″为等腰三角形，则

A′G=A″G=nh+t

再从△A″DF和△A‴DF得

则

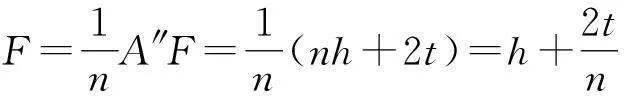
由图可知，物A到像A‴的距离

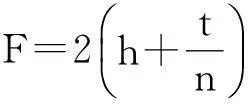
图4

解法3(逐次成像公式法)：如图4所示， 物A通过玻璃砖上表面折射后第一次成像，像点为A′，根据折射成像公式得

得v1=-nu1=-nh,式中的负号表示A′为虚像， 像点A′至玻璃砖上表面的距离为nh.

第二次是通过玻璃砖下表面反射成像，第一次所成的像A′为第二次成像的实物，物距为

u2=nh+t

根据平面镜反射成像公式

得

v2=-(nh+t)

负号表示所成的像为虚像，所成的像为A″，A″至玻璃砖下表面的距离为nh+t.

第三次成像是通过玻璃砖上表面折射成像，第二次所成的像A″是第三次成像的实物，物距

u3=nh+2t

根据折射成像的公式得

得

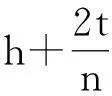
物点A位于玻璃砖的上方距玻璃砖的上表面为h处，即得像A‴离物A的距离为