巧用等效法解决阶梯型物理问题

巧用等效法解决阶梯型物理问题*

尹德兴

(云南师范大学物理与电子信息学院云南 昆明650500;武定县第一中学云南 楚雄651600)

彭朝阳

(云南师范大学物理与电子信息学院云南 昆明650500)

*云南师范大学物理教师教育课程改革研究项目.

摘 要：举例说明，用物理作用的等效替换，可巧妙解决形式多样的阶梯型物理问题.

关键词：等效替换阶梯型物理问题

收稿日期：(2014-11-04)

等效替换法就是在保证某一方面效果相同的前提下，用理想的、熟悉的、简单的对象、过程、现象替换实际的、陌生的、复杂的对象、过程、现象的思想方法.等效替换法能使一些繁杂、困难问题的处理得以简化，能使一些难以直接研究的问题得以解决.等效替换法不仅是物理学研究问题的一种主要方法，也是解物理题的常用方法.解物理题运用等效法，不仅可以化难为易，化繁为简，化陌生为熟悉，起到事半功倍的效果，还能提高学生对物理知识的理解和运用，并能促进其思维能力的发展和提高，培养学生分析、概括问题和推理的能力.

等效替换法在解物理题方面的应用，主要有模型的等效替换、过程的等效替换、本质的等效替换、作用的等效替换等.本文仅从物理作用的等效替换方面举例阐述，巧用等效替换法解决阶梯型物理问题.所谓物理作用的等效替换是指，在某一物理过程中对外界所产生的作用效果相同出发，来研究物理事物的本质和规律，分析和处理物理问题的一种思维方法.所谓阶梯型物理问题是指一类形似楼梯一样的物理问题.

1滑轮组分析

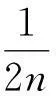
下面举例说明巧用等效替换法分析两类典型的阶梯型滑轮组问题.

【例1】如图1所示，由n个动滑轮组成的阶梯型滑轮组，在忽略滑轮自重和摩擦的情况下，重物G匀速上升时，求拉力F多大.

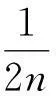
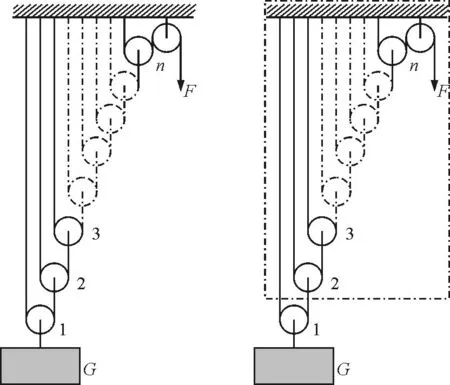
图1 图2

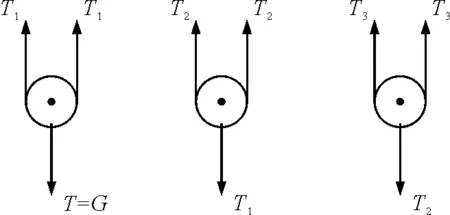
图3

同理，对动滑轮2受力分析得

对动滑轮3受力分析得

以此类推.对动滑轮n受力分析得

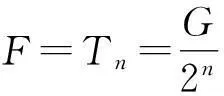
【例2】如图4所示，由n个动滑轮组成的阶梯型滑轮组，在忽略滑轮自重和摩擦的情况下，重物G匀速上升时，求拉力F多大.

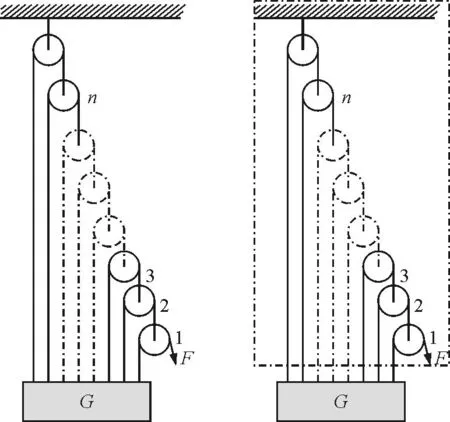
图4 图5

如图5所示，把虚线框等效看做一个整体，利用等效替换法分析，对重物进行受力分析，如图6所示.

图6

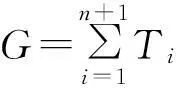
即

所以拉力

2等效电阻的计算问题

等效电阻的计算问题也是利用等效替换法的一个好例子.实际电路一般比较复杂.要计算等效电阻，需进行电路分析，搞清各电阻之间的串并联关系.下面举例说明巧用等效替换法解决阶梯型电路的等效电阻问题.

【例3】如图7所示，已知电阻R1,R2,R3组成无穷长阶梯型电路，求A,B两端的等效电阻Rx.

解法1： 利用等效替换法求解等效电阻Rx

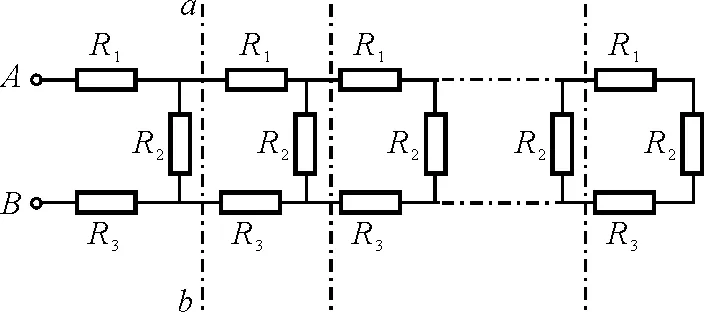
图7

假设A，B两端电阻为Rx，如图7所示，则a，b间的等效电阻亦为Rx，即

整理后得

解得

因为Rx必须大于(R1+R3),所以舍去

故得

为验证等效替换法解此题的正确性，我们不妨使用传统的节点法再解一次.

解法2：利用节点法求解等效电阻Rx

在节点Ⅰ，设流入节点的电流为I,流出节点的电流分别为I1和I1′,如图8所示.

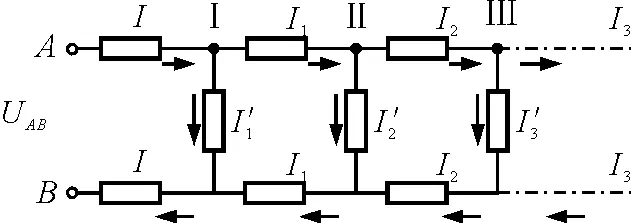
图8

I1=kI

(1)

I1′=(1-k)I

(2)

在节点Ⅱ，设流入节点的电流为I1,流出节点的电流分别为I2和I2′,如图8所示.

由阶梯形电阻连接的规则性可得出，在节点Ⅱ有

将式(1)、(2)代入，整理得

I2=k2I

(3)

I2′=k(1-k)I

(4)

由于节点Ⅰ和节点Ⅱ之间的并联电路电压相等得

I1′R2=I1(R1+R3)+I2′R2

(5)

将式(1)、(2)、(4)代入式(5)得

(1-k)IR2=kI(R1+R3)+k(1-k)IR2

整理后得

R2k2-(R1+2R2+R3)k+R2=0

(6)

解得

(7)

根据题意得k应该小于1，故舍去

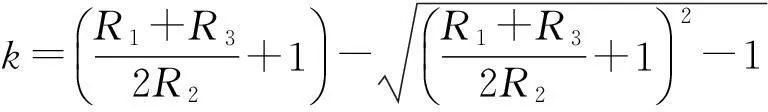
(8)

由欧姆定律得

UAB=I(R1+R3)+I1′R2=

I(R1+R3)+(1-k)IR2=

(9)

UAB=IRx

(10)

将式(9)代入式(10)得

两种解法结果完全相同，但是利用等效替换法求解，明显比利用节点法求解容易得多.

3等效电容的计算问题

等效电容的计算问题是利用等效替换法的又一个好例子.要计算等效电容，则需搞清各电容之间的串并联关系.下面举例说明巧用等效替换法解决阶梯型电路的等效电容问题.

【例4】如图9所示，已知电容C1,C2,C3组成无穷长阶梯型电路，求A,B两端的总电容Cx.

图9

解法1：利用等效替换法求解等效电容Cx

假设A，B两端电容为Cx，如图9所示，则a，b间的等效电容亦为Cx，即

整理后得

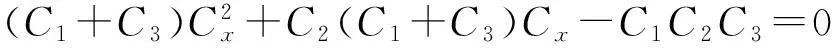
解得

因为Cx必须为正，所以舍去

故得

同样，为验证等效替换法解此题的正确性，我们不妨使用传统的节点法再解一次.

解法2： 利用节点法求解等效电容Cx

在节点Ⅰ，设节点Ⅰ周围电容器的带电量分别为q，q1和q1′，如图10所示.

图10

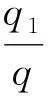
q1=kq

(11)

q1′=(1-k)q

(12)

在节点Ⅱ,设节点Ⅱ周围电容器的带电量分别为q1，q2和q2′，如图10所示.

由阶梯形电容连接的规则型可得知，在节点Ⅱ有

将式(11)、(12)代入，整理得

q2=k2q

(13)

q2′=k(1-k)q

(14)

由于节点Ⅰ和节点Ⅱ之间的并联电路电压相等得

(15)

将式(11)、(12)、(14)代入式(15)得

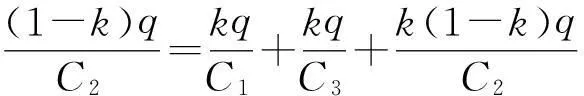
(16)

整理后得

C1C3k2-(2C1C3+C1C2+C2C3)k+

C1C3=0

(17)

解得

根据题意得k应该小于1，故舍去

得

(18)

由分压原理的得

UAB=U1+U2+U3=

(19)

设A，B之间的等效总电容为Cx，则有

代入式(19)即得

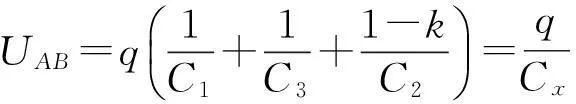
(20)

式(18)代入式(20)解得

两种解法结果完全相同，但不难看出，等效替换法求解，明显要比节点法求解容易得多.

结论：从以上例解可以看出，采用等效替换法不仅可以将问题转换为我们熟悉的物理模型，而且可以简化解题步骤.在教学中教师应启发学生多思考、多类比，通过等效替换来提高知识的应用能力，培养学生的发散思维和创新思维能力.

如果教师在教学时能引导学生在形成物理概念、解答物理习题过程中运用等效法，使学生明确在分析和解答物理问题时，需要将复杂的问题通过等效法进行提炼、简化，找出问题的本质，学生就会在学习中逐渐尝试用等效法开创性地解决问题.在掌握知识的同时又能灵活运用知识，促进知识、技能的迁移，在学习过程中体会到乐趣，从而调动学习的积极性、主动性，主动地探索物理，进而提高科学素养.等效思维具有一定的灵活性和技巧性，必须在认真分析物理特征的基础上，进行合适的等效变换，才能获得简捷的求解方法.

参 考 文 献

1阎金铎,田世昆．中学物理教学概论.北京：高等教育出版社，1999

2许国梁.中学物理教学法.北京：高等教育出版社，1993

3王承贵.物理中的等效代换.辽宁教育学院学报，1998(5)

4梁灿彬,秦光戎,梁竹健.电磁学.北京：高等教育出版社，1980

5张小溪.规则连接的电阻、电容网络的数学模型.大学物理，1999(2)