调整协变量的多位点关联分析方法及其在酗酒数据中的应用

邓舒方，王昱泉，胡跃清

(复旦大学 生命科学学院 生物统计学与计算生物学系，上海 200433)

得益于高通量测序技术的快速发展，我们获得了大量全基因组范围内的遗传变异数据，而如何有效地利用它们进行基因与疾病的关联分析是生物统计学的重要任务.在早期的全基因组关联分析(Genome-Wide Association Study, GWAS)研究中，人们一般以单个单核苷酸多态性(Single Nucleotide Polymorphism, SNP)为单位进行疾病的关联分析[1-2]，而随着研究的深入，人们发现复杂疾病的发生往往涉及多个位点，其中一些位点的效应可能较弱，此时，单SNP分析可能会漏筛一些致病位点[3-7].为了提高检验功效，需要对多个SNP进行整合分析： 如果存在一个致病位点，由于相邻位点间存在连锁不平衡，故相邻位点也会与疾病关联，将这一段区域内的位点进行联合分析能最大程度地提高检验功效.基于这一思想，Wang等[8]提出了一种针对病例对照数据的多位点联合关联分析方法SLIDE(the test Statistic incorporating Linkage Disequilibrium)，该方法能够有效利用位点间的连锁不平衡(Linkage Disequilibrium, LD)信息对统计量的方差协方差矩阵进行计算，从而提高检验功效.

然而，遗传学研究数据中常常包含一些协变量信息，如年龄[9]、种族[10-11]等，这些协变量信息在进行遗传位点与性状的关联性检测中有着重要作用，如果不对这些协变量信息进行适当处理，可能会带来分析结果的偏差或是检验功效的降低[12].当协变量既与预测变量相关也与响应变量相关时，若在探究预测变量和响应变量的关联性过程中不考虑因此带来的混淆影响，会增加分析结果的假阳性率[13].此外，调整协变量在某种程度上能够通过降低统计量方差来增加预测模型的准确度[14-15].因此，在遗传关联分析中，对协变量进行调整是有意义的.

在多位点关联分析中，传统的调整协变量的方法主要有两类： 第一类是将响应变量对预测变量及协变量同时回归[16]，如SKAT[17]及SKAT-O[18]对应的调整协变量方法;第二类是将响应变量对协变量进行回归得到残差，将残差再与预测变量进行关联分析[19]，如传统的残差回归[20-21]以及SSU/aSPU[22]对应的调整协变量方法.这两类方法都依赖于假设的疾病产生模型，普适性不高.故我们基于SLIDE这一不依赖于模型的多位点非参关联检测方法，提出一种对基因型用倾向得分进行逆概率加权[23-24]的调整协变量关联分析方法SLIDEa.

为了检验SLIDEa方法的表现，我们计算了不同随机模拟场景下该方法与文献中现有方法的第一类错误率以及检验功效.模拟结果表明，它在基因与协变量交互作用存在或基因间效应方向相反时均具有较好表现.随后我们将SLIDEa应用至酗酒相关遗传学合作研究数据集COGA中，找到了线粒体外膜脂代谢酶基因OPA3、催产素受体基因OXTR等数个与酒精成瘾性相关的基因[25-27]，这表明了SLIDEa方法的有效性并能为后续的生物学研究提供理论指引.

1 符号和方法

1.1 现有方法介绍

SKAT方法是Wu等[17]于2011年提出的一种关联分析方法，它基于病例对照数据的如下模型

其中：G是预测变量；D是二分类响应变量；Z是协变量.原假设下所有预测变量与响应变量无关联，其统计量为

SKAT-O方法是Lee等[18]于2012年提出的，它其实是SKAT的统计量与Burden检验统计量的加权和.

Qρ=(1-ρ)QSKAT+ρQBurden，

其中：ρ为合并方法Burden所占权重，0≤ρ≤1;Pρ为统计量Qρ的P值.在原假设下，Qoptimal服从混合卡方分布.考虑到协变量Z容易纳入到回归模型中，我们用adj_SKAT/adj_SKAT-O分别表示调整了协变量Z的方法.

aSPU是Pan等[22]于2009年提出的一种关联分析方法.对于病例对照研究，aSPU从模型

得到得分统计量向量

其中：ξj为每个位点得分统计量的权重，1≤j≤m.而aSPU统计量为

其中：γ为权重；PSPU(γ)为检验统计量TSPU(γ)的P值；Γ是γ的一个取值范围，如在本文的随机模拟中，Γ={1，2，4，∞}.特别地，当Γ={2}时，aSPU就是SSU.

在协变量存在的情况下，adj_aSPU与adj_SSU首先将响应变量对协变量做回归，得到残差项，随后将残差项当成新的响应变量得到调整协变量后的得分统计量向量，后续与aSPU/SSU计算方式相同.adj_resi与adj_aSPU类似，先将响应变量对协变量做回归，得到残差项，随后将残差项当成新的响应变量对预测变量做回归.

1.2 多位点关联分析方法SLIDE介绍

对病例对照组数据，Wang等[8]在回溯性框架下提出了一个能同时对m个遗传变异位点进行关联分析的统计量TSLIDE，其U向量及其方差协方差矩阵表达式如下：

其中：nA表示患病个体数；nU为健康个体数；第i个个体的患病状态记为Di，其中Di=1表示患病，Di=0表示健康；Gi=(Gi1，Gi2，…，Gim)T为第i个个体的m个位点基因型，其中Gij表示第i个个体在第j个位点的基因型，Gij={0，1，2}，它表示较小等位基因在该位点上的个数.U统计量反映了多位点基因型在病例组和对照组之间的差异.在原假设H0： 这m个位点均与疾病无关联成立的条件下，患病人群与健康人群的多位点基因型均值无差异，从而E(U)=0，对应的方差协方差矩阵为

Cov(G)=(σjk)m×m，σjj=2pj(1-pj)，σjk=2δjk， 1≤j≠k≤m，

其中：G表示研究所在的总体中某个体在m个位点的基因型；pj为第j个位点的较小等位基因频率，1≤j≤m;δjk为第j、k个位点间的LD值，δjk=pjk-pjpk，pjk为在一条染色单体上第j、k位点基因均为较小频率等位基因的概率，检验统计量为

在原假设下，TSLIDE渐近服从自由度为m的卡方分布，从而方便得到它的P值.

1.3 基于SLIDE的逆概率加权调整协变量方法

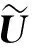
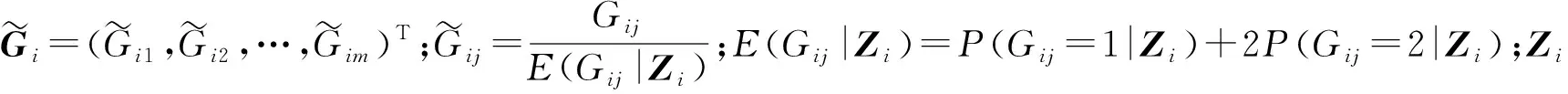
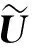
非对角元(j，k)(j≠k)为

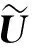
2 随机模拟研究

2.1 数据产生模型

我们先通过模型产生10万个个体的协变量、基因型信息和性状值，再依据0/1型性状从相应人群中各随机抽500个个体作为病例和对照用于下一步的多位点关联分析.数据产生模型具体分为3步：

(i) 产生p维协变量信息Z.对于第i个个体，1≤i≤n=100 000，Zi=(Zi1，Zi2，…，Zip)T，其中Zi1，Zi2，…，Zip相互独立，均服从Bernoulli(0.5)分布.

(ii) 由Zi通过有序logistic回归产生第i个个体基因型Gi=(Gi1，Gi2，…，Gim)T，其中位点j的基因型Gij生成模型是

其中： 1≤j≤m，m取值为5或50；(ε1，ε2，…，εm)T来自于均值为0的m维正态分布；εj、εk间的协方差Cov(εj，εk)=ρ|j-k|，1≤j≠k≤m；ρ的大小反映了位点间的相关程度；模型中的μgj根据对应位点的最小等位基因频率(Minor Allele Frequency, MAF)及样本协变量信息计算得到，即μgj需要满足等式E(Gij)=2×MAFj，MAFj表示第j个位点较小等位基因在人群中的频率；αj=(αj1，αj2，…，αjp)T表示p维协变量对第j个基因位点的影响.

(iii) 由Zi、Gi通过logistic回归产生性状Di：

其中：β0反映人群发病率；βg为位点对性状的m×1效应向量；βz为协变量对性状的p×1效应向量；βgz为位点与协变量的交互项对性状的m×p效应矩阵.

对于第一类错误率，我们共考虑SNP个数(5或50)、协变量维数p(1或2)和位点类型(全为常见变异(Common Variant, CV)或CV与罕见变异(Rare Variant, RV)交替出现)的6种不同组合情形.CV的MAF从0.1至0.4中随机产生;RV的MAF从0.005至0.01中随机产生;每种情形中又根据协变量对性状是否有效应、ρ=0或ρ=0.5分为4种子情形;每个情形下重复模拟次数为1 000，显著性水平为0.05;为了计算第一类错误率，设β0=ln0.1、位点对性状无效应、位点与协变量交互项对性状也无效性，详细参数设置见表1，其中：α=(α1，α2，…，αm)为p×m参数矩阵.

表1 原假设下的参数设置Tab.1 Parameter setting under H0

随后，我们根据SNP个数、协变量维数、位点MAF、位点与协变量交互作用方向的不同设置了8种情形来比较各种方法的功效： 当SNP个数为5时，假设前两个位点为致病位点；当SNP个数为50时，假设第1、2、6、7个位点为致病位点，其中常见致病位点对性状效应值的取值范围为0.05～0.3、罕见变异位点效应值范围为0.09～1.09;情形1～情形4中设置了5个SNP及一维协变量，考虑了是否仅含常见变异、位点与协变量交互作用方向相同/相反下不同组合的情形，用以探究不同位点类型、不同基因与协变量相互作用效应方向下各种方法的表现;情形5～情形6将协变量扩展为二维，用以探究在二维协变量情况下各方法功效差异;情形7～情形8将SNP个数扩大为50，用以探究各方法在多SNP个数下的表现;在情形1～情形8中，又考虑了致病位点对性状效应方向相同/相反两种子情形，如在5个SNP中，βg=(ln1.05，ln1.05，0，0，0)T是当位点效应方向相同的情况，那么与之对应βg=(ln1.05，ln(1/1.05)，0，0，0)T则为位点效应方向相反情况;具体参数设置见表2，模拟研究重复次数为1 000，显著性水平为0.05.

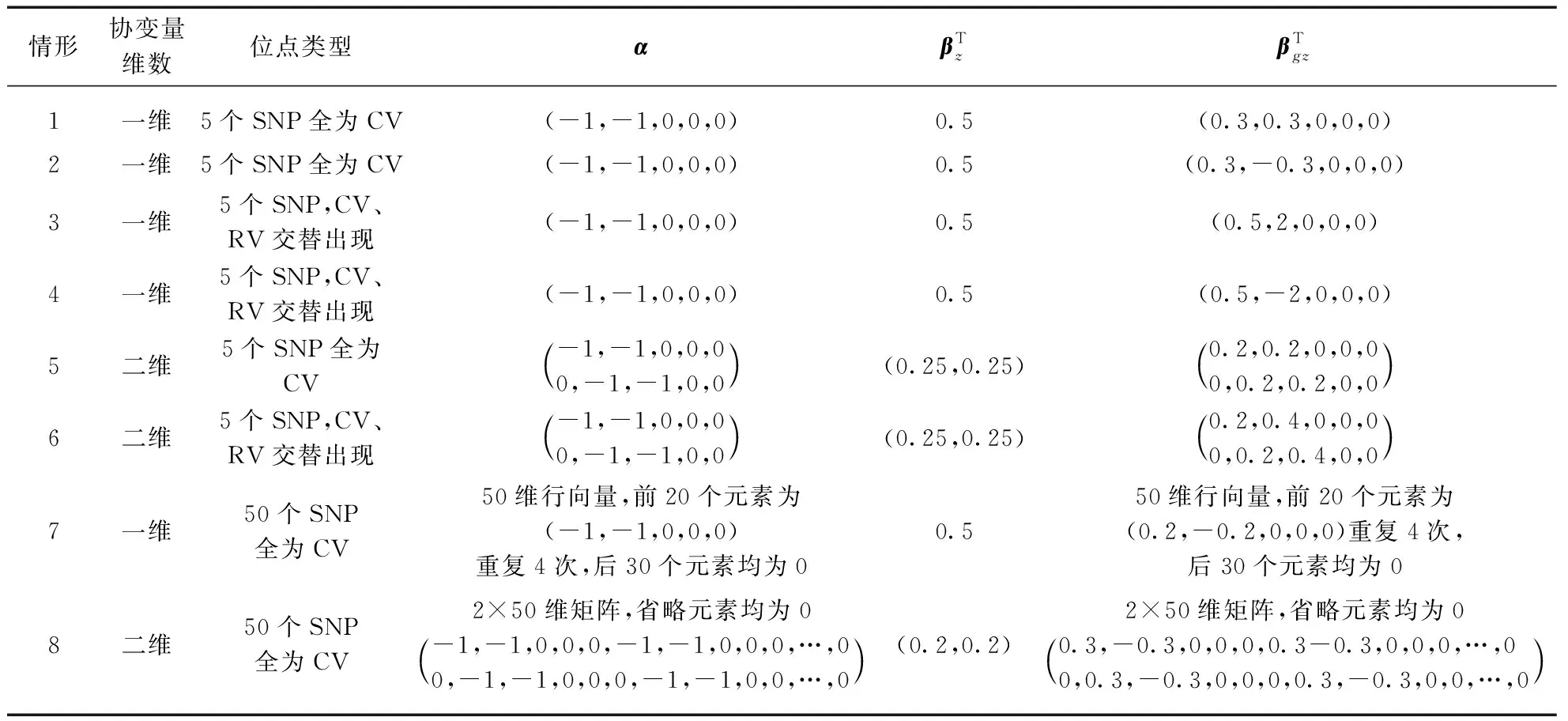
表2 计算功效的参数设置Tab.2 Parameter setting for power evaluation

2.2 随机模拟结果

表3展示了各方法及其对应的调整协变量方法在原假设情形1～情形6下的第一类错误率.从中不难发现当βz不为零时，未进行协变量调整的方法的第一类错误率明显大于0.05，这说明当协变量既与基因型又与性状相关时，不考虑协变量直接进行基因与性状的关联性分析会控制不住第一类错误率，故在这种情形下，对协变量进行调整是减小假阳性率的有效手段.且当SNP个数增加至50个时，SLIDEa方法仍能控制住第一类错误率.

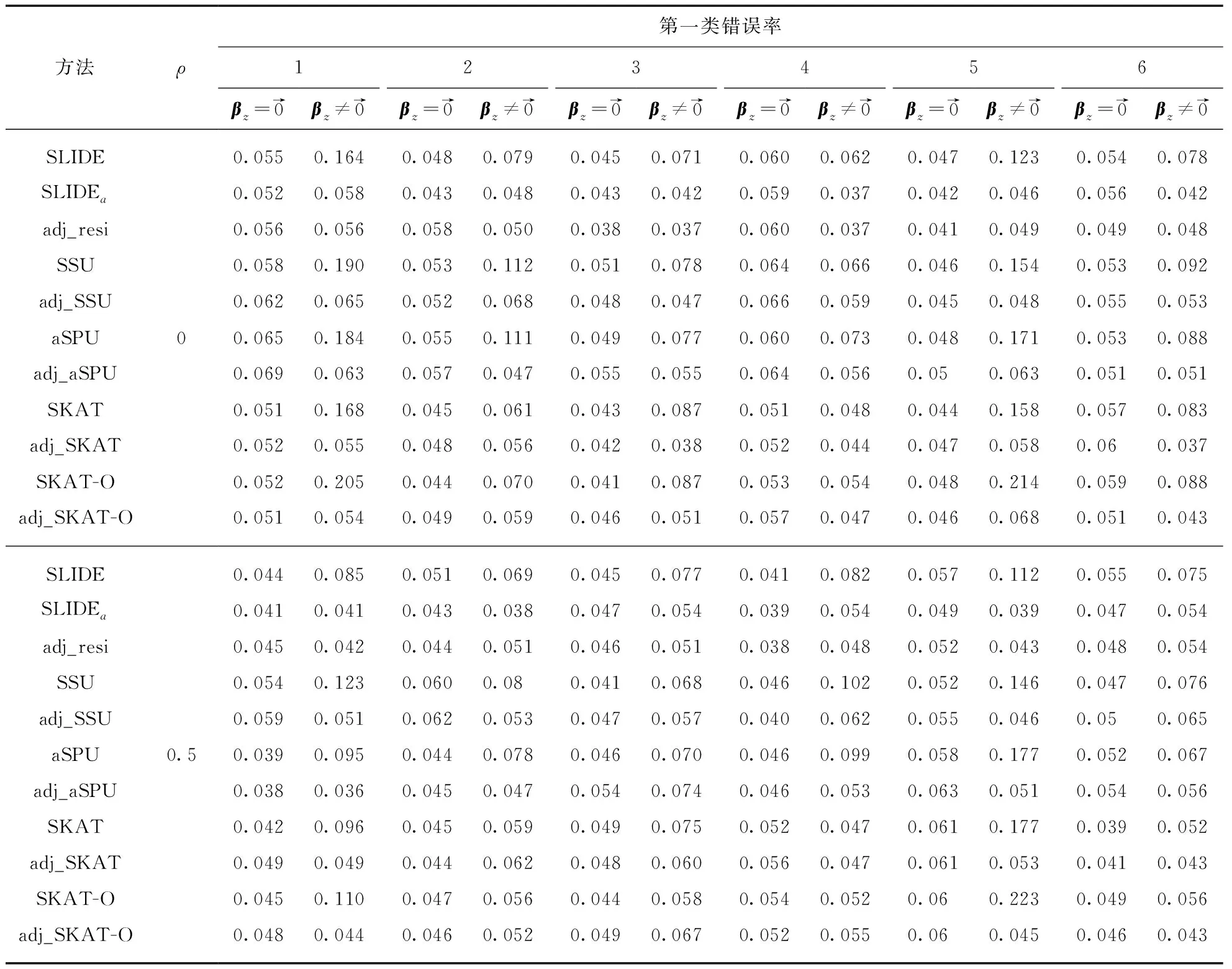
表3 原假设中各情形下各方法的第一类错误率Tab.3 Type I error rate for each scenario under H0

接着在α、βz均不为零，即协变量既与基因型有关也与性状有关的情形下对各调整协变量方法进行功效比较.图1(见第774页)和图2(见第775页)为对立假设下8种情形各方法的功效比较.当SNP个数为5、协变量为一维时，如情形1～情形4中结果所示，无论不同位点对性状效应方向一致还是相反，在位点与协变量存在交互作用的情况下，本文提出的SLIDEa方法均相较于其它多位点调整协变量关联分析方法具有优越性，并在不同位点与协变量交互项效应方向相反时它仍能保持明显优势;当关联分析位点包含罕见变异位点时，SLIDEa方法虽然仍能保持优势，但这种优势在关联分析位点全为常见变异位点时表现得更为明显;当增加协变量维数至二维、保持SNP个数不变时，如情形5～情形6中结果所示，当位点与协变量存在交互作用的情况下，SLIDEa的表现均优于其他方法;当SNP个数增加至50个、位点全为常见变异时，无论协变量维数是一维还是二维，SLIDEa同样具有较好表现.

图1 不同致病位点对性状效应方向相同时对立假设情形1～情形8下各方法功效比较Fig.1 Power comparison for scenarios 1 to 8 under Ha while the effect directions of these loci are identical注： 该表展示了对立假设情形下当不同致病位点对性状效应方向相同时，情形1～情形8下各个方法的功效;其中βg为第一个位点对性状的回归系数.

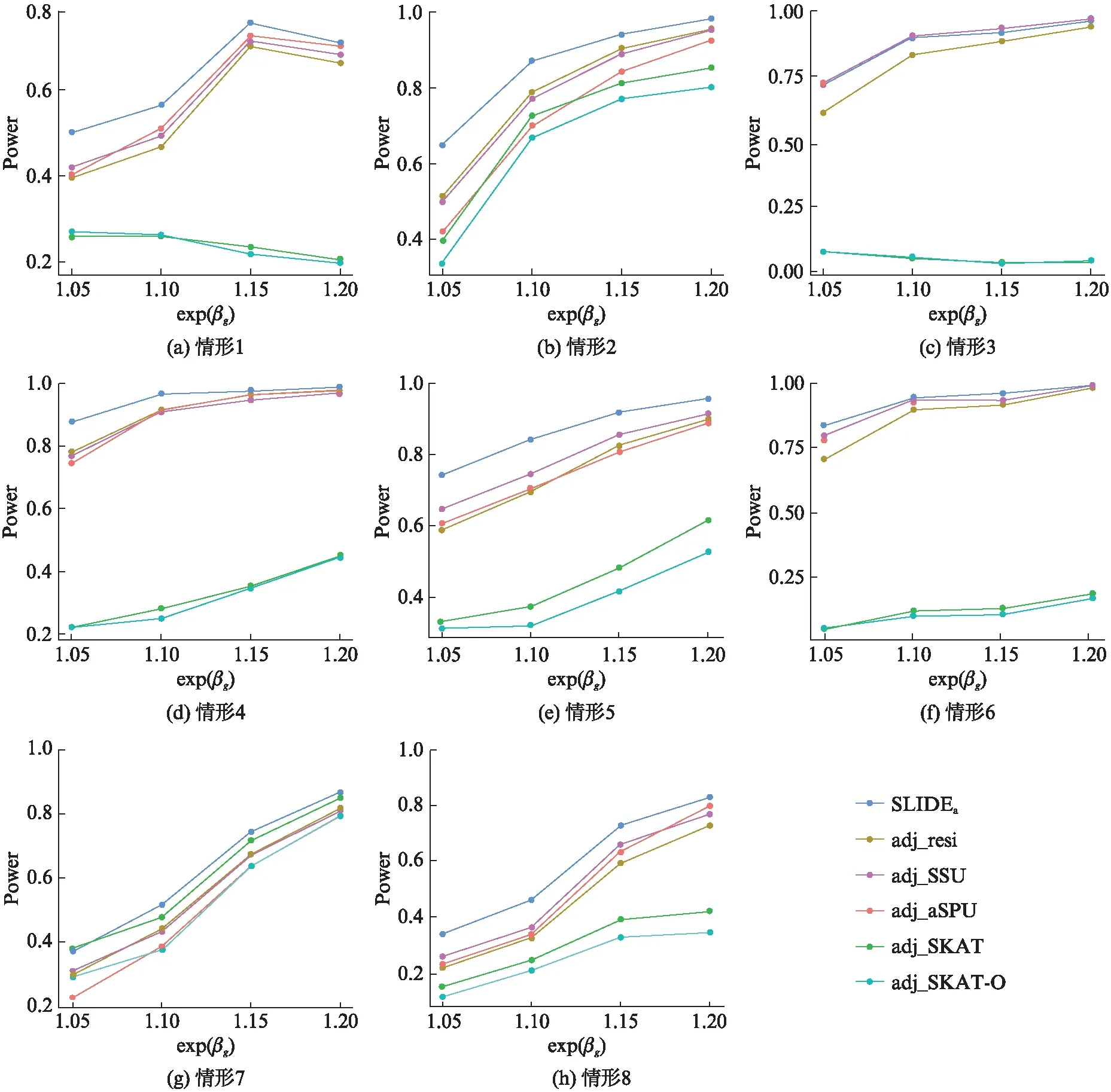
图2 不同致病位点对性状效应方向相反时对立假设情形1～情形8下各方法功效比较Fig.2 Power comparison for scenarios 1 to 8 under Ha while the effect directions of these loci are opposite注： 该表展示了对立假设情形下当不同致病位点对性状效应方向相反时，情形1～情形8下各个方法的功效;其中βg为第一个位点对性状的回归系数.

综上可得，SLIDEa适用于基因和环境存在交互作用时的基因与性状间关联分析，无论位点对性状的效应方向相同或相反、不同位点与协变量交互项效应方向相同或相反，它均能保持其优势.TSLIDEa统计量在构建过程中未依赖任何疾病发生模型，而其他方法，如adj_resi、adj_ aSPU等虽然也是基于无模型假设，但在调整协变量时，需要将性状对协变量进行回归，从而得到性状的残差，再用残差与基因进行关联分析.因此，在用其它方法调整协变量时，若是模型假定与真实模型不一致，会导致统计量功效降低.SLIDEa在调整协变量和关联分析中都不依赖于实际疾病发生模型，因此该方法是较为稳健的，受疾病真实发病模型的影响较小.

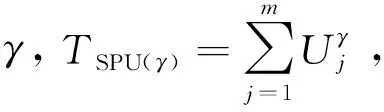
3 实际数据分析

酗酒相关遗传学合作研究数据(The Collaborative Study on the Genetics of Alcoholism, COGA)的参与者来自于美国7个不同地区，它收集了详细的酒精依赖诊断所需信息.我们分析的是COGA中一部分依据《精神障碍诊断与统计手册第4版》(DSM-Ⅳ)标准对进行酒精成瘾性评估划分为病例组及对照组后筛选出来的病例对照研究数据，包含共1 945人的全基因组测序数据和年龄、性别、每日吸烟量等30个潜在酗酒相关协变量因子.除去测序缺失的数据，我们最终得到1 913个个体共包含107万个遗传位点、18 946个基因的测序数据.接下来，我们在NCBI(National Center for Biotechnology Information)上筛选出304个已报导的与酒精成瘾性相关的基因，用SLIDEa、aSPU、SKAT和SKAT-O对应的协变量调整方法对其中在COGA测序数据中出现的267个基因逐一进行关联分析.我们将年龄和家庭酗酒史作为协变量进行调整，来探究在给定年龄及家族史的情况下与酗酒相关的关联性位点.

表4展示了用SLIDEa得到的前10位显著基因和对应P值及其他方法得到的P值.从该表中可以看出，各个方法均能发现这些基因，其P值也在相近水平，但是SLIDEa的P值会稍低一些.通过文献检索，我们可以得出这些基因与酗酒成瘾性具有一定关联.例如，其中的CHRNB2为神经元烟碱类受体，能够与乙酰胆碱或尼古丁结合控制钠、钾离子通过细胞膜，这一基因与尼古丁依赖高度相关[28]，后续全基因组关联分析中也发现它还与酒精成瘾性相关联[29-30];OPA3基因编码蛋白参与线粒体内膜净化[31]，而线粒体内膜参与酒精代谢[32]，已发表的GWAS研究也有发现OPA3与酒精成瘾性相关[25];而OXTR作为G蛋白偶联受体，也在多个基因与酒精成瘾性GWAS研究中被检测到[26-27].这些基因与酒精成瘾性的关系也进一步说明了SLIDEa的可靠性.

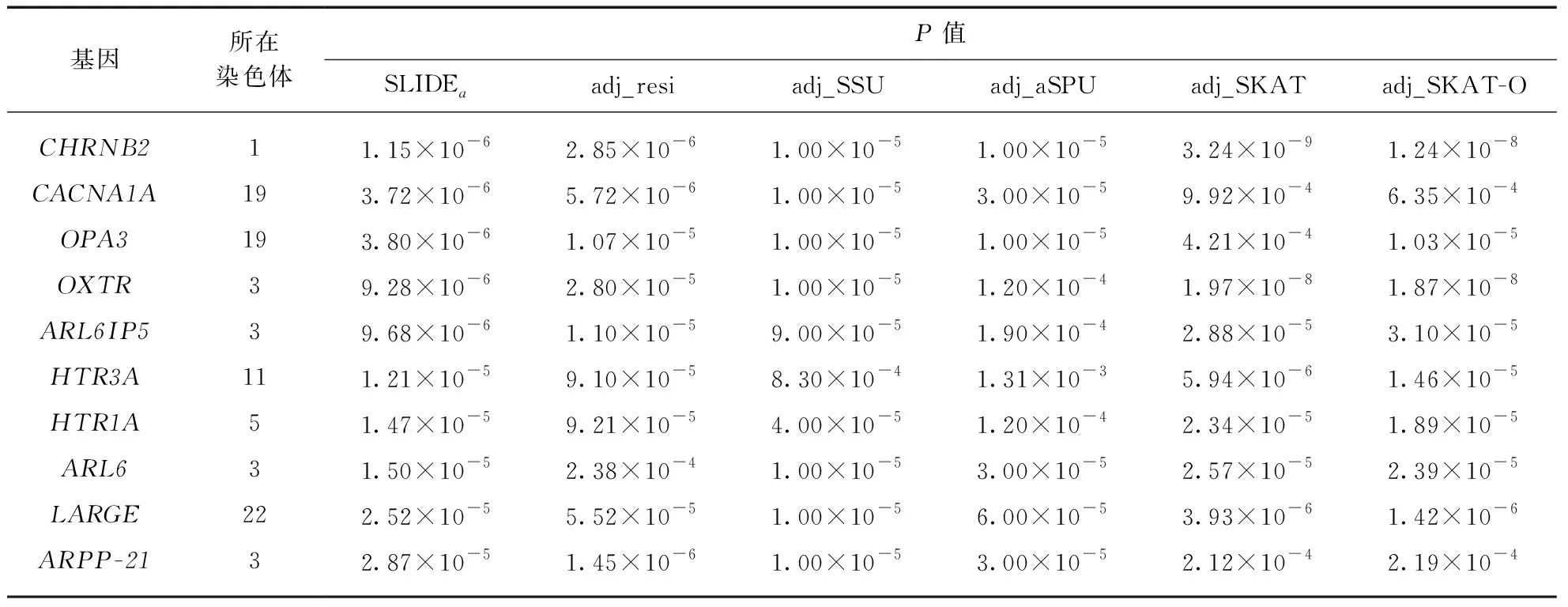
表4 COGA数据利用SLIDEa得到的前10位显著基因及所有方法的P值Tab.4 P-values for top 10 significant genes obtained from SLIDEa on COGA data

这10个基因由Metascape工具(网址： http：∥metascape.org/)得到的注释结果详见表5.将这10个基因输入PANTHER网站(网址： http：∥www.pantherdb.org/)做基因富集分析，可以得到4个GO通路，分别是GO： 0042220(P=1.24×10-2)，GO： 0051952(P=4.54×10-4)，GO： 0043269(P=4.61×10-2)，GO： 0003008(P=2.61×10-2).这4个基因通路分别与可卡因、胺转运、离子转运和系统过程相关，和酒精成瘾性的关系尚不明确，有待进一步研究.

表5 COGA数据利用SLIDEa得到的前10位显著基因注释结果Tab.5 Annotation result of top 10 significant genes obtained from SLIDEa on COGA data

4 总结与讨论

已有的研究结果表明了在协变量既与基因有关也与性状有关时调整协变量的必要性.为了消除关联分析时协变量带来的混淆影响、降低关联分析方法的假阳性率，本文在多位点联合关联分析方法SLIDE的基础上，提出了一种对基因型用倾向得分进行逆概率加权的调整协变量关联分析方法SLIDEa，其中的协变量可以是多维的.模拟结果显示，当致病位点为常见变异时，与aSPU、SKAT等调整协变量方法相比，在基因对性状效应相反或存在基因与协变量的交互作用时，SLIDEa具有一定优势;而当致病位点有较多罕见变异时，它的效果不是很理想，这是因为在等位基因频率几乎为0时，用样本数据估计U的方差会出现问题，从而使SLIDEa的功效降低.SLIDEa的另一优势在于它的构建过程不依赖于疾病产生模型，这使得它的适用范围较广.随后，我们将提出的方法应用于酗酒遗传学实际数据COGA的分析中，找到的显著性基因可以用来做进一步的生物学基础研究.

本方法仍有几个方面值得改进： 1) 需要提升它在存在较多罕见变异位点时的效果，与SLIDE相比，它无法利用外部大样本数据来估算统计量的方差，所以在致病位点全为罕见变异的情况下，它的表现不是很理想.2) 当关联分析SNP位点数目m大、样本量不大时，存在数据稀疏性，此时统计量可能会不服从卡方分布.此外，统计量方差中涉及到与m2同阶多的条件期望的计算;故当关联分析位点数目过多时，可以根据位点间的位置将多位点划分成数目较小的一些片段，得到这些片段的P值后整合得到整个基因的P值.