多元有序Logistic模型在车险索赔次数预测中的应用

李浩男

（南开大学金融学院，天津300350）

一、引言

车险定价一直以来都是研究的热点，2020年9月19日启动的商业车险综合改革，对车险定价的精确性和合理性提出更高的要求，是我国车险高质量发展的重要契机。广义线性模型作为车险索赔的建模分析重要手段之一，自1972年Nelder J A和Wedderburn R 首次给出定义以来，学术界不断为该方法增加新元素，例如Anderson等（2004）［1］对指数分布族的深入讨论；同时国内外相关的著作也越来越丰富，如Frees（2010）［2］、孟生旺等（2015）［3］。

由于免赔额与无赔款优待等条款的存在，实务中车险索赔数据存在大量的零次索赔，传统的广义线性模型无法解决索赔数据零膨胀、过离散以及异质性的特征。此时，解决零膨胀的一个有效的方法是将模型分为零点概率和计数分布两个部分，即（a，b，1）型的零膨胀模型。Yip 和Yau（2005）［4］首次使用零膨胀模型分析了车险索赔次数，分别讨论了泊松分布与负二项分布下的零膨胀模型。为了提升拟合结果，进一步完善零膨胀模型一直是研究热点。孟生旺和杨亮（2015）［5］基于传统零膨胀模型增加了随机效应，以此分析索赔数据组内的相依性。张连增和王缔（2019）［6］对比零膨胀模型与Hurdle 模型，实证结果显示零膨胀负二项模型更好。徐昕（2020）［7］探讨了零膨胀广义泊松模型的推广形式，并给出了模型和参数估计方法。

为了进一步解决零膨胀特征导致的过离散和异质性问题，在零膨胀模型的基础上提出了混合泊松模型（Mixed Poisson， MP）。 Joe 和Zhu（2005）［8］、Nikoloulopoulos和Karlis（2008）［9］先后对比了不同的混合泊松模型，分析了索赔频率数据的零膨胀、过离散以及厚尾特征。王选鹤等（2018）［10］研究了零膨胀混合泊松的有限混合模型，实证结果表明该模型有助于改进对索赔次数的估计结果；殷崔红等（2019）［11］讨论了开放式的混合泊松模型，提升了模型的自适应性。

综合已有研究可以发现，学者们大多使用混合泊松或零膨胀泊松来研究索赔次数，在一定程度上可以解决零膨胀、过离散和尾部概率的问题。但是在应用层面，此类模型计算复杂、模型求解比较困难，同时参数难以直观解释；另一方面，确定混合泊松模型的混合个数时仍包含较大的主观性。索赔次数的零膨胀问题可以视为（a，b，0）型计数模型的“后遗症”，因为不同次数之间的发生概率需满足递推关系（Panjer，1981）［12］，使用极大似然估计方法会受到该递推关系的影响。大量零次索赔的存在将迫使模型给予零点概率过高的权重，从而“拉偏”了对尾部风险的估计，导致模型结果并不理想。

为了避免计数分布递推关系对模型的影响，已有学者使用二元Logistic 回归研究车险索赔次数（张连增和孙维伟，2012；Duan等，2018）［13，14］，但是这些讨论仅限于是否发生索赔，只使用了索赔次数中的部分信息。本文将索赔次数视为有序分类变量，引入多元有序Logistic 回归模型（Ordered Lo⁃gistic Regression，OLR），该模型作为Logistic模型的一个重要分类，其较多应用于医学分析中，如Kanbayashi 等（2018）［15］利用OLR 模型探究了不同程度胆碱能综合征的发病因素。在保险领域，刘威和刘昌平（2018）［16］使用该模型分析了社保对农村老年人健康状况的影响，讨论了模型异质性。

本文采用OLR 模型分析索赔频率数据。首先，参考Agresti（2003）［17］对OLR 连接函数的讨论，选择了3种不同的连接函数建立OLR模型；其次，基于OLR模型的概率意义，定义了相对风险系数，以分析风险因素变动引起的索赔概率的相对变化；最后，利用一组车险索赔数据，实证分析的结果验证了该方法在车险索赔领域的实用价值。OLR模型相较于已有方法在模型构建、参数估计、结果分析上都更为容易。

二、模型构建与评价

传统的（a，b，0）型计数分布必须满足式（1）（Panjer，1981）［12］：

上式中只有a、b两个参数，3 个概率值构成的两个方程即可完全确定分布。使用传统分布估计时，当索赔次数超过3 次以后，索赔次数估计值会出现较大偏差（薛智雯，2018）［18］。即使是将零点概率单独剥离出来的零膨胀模型，也仍然没有摆脱这种递推关系，模型估计的灵活性同样受到限制。零膨胀混合泊松模型通过多个分布的混合扩展了参数的个数，提升了模型估计的准确性，但是一方面，混合模型降低了参数的可解释性，另一方面，混合个数的确定包含了过多的主观性。

为了避免计数分布递推关系的影响，本文将索赔次数作为分类变量，应用多元有序Logistic 回归模型，该模型可拓展性较强，并且结果具有概率意义，解释力更强。索赔次数的高低可以反映驾驶员风险等级的排序，所以将索赔次数视作分类变量在实际意义上是合理的。

（一）模型构建

OLR 模型作为广义线性模型的一个重要分支，其连接函数是累积概率的转换形式。本文实证结果表明，不同的连接函数对模型的预测结果影响很小，故选择更为平滑的Logit 连接函数，构建的OLR模型如下：

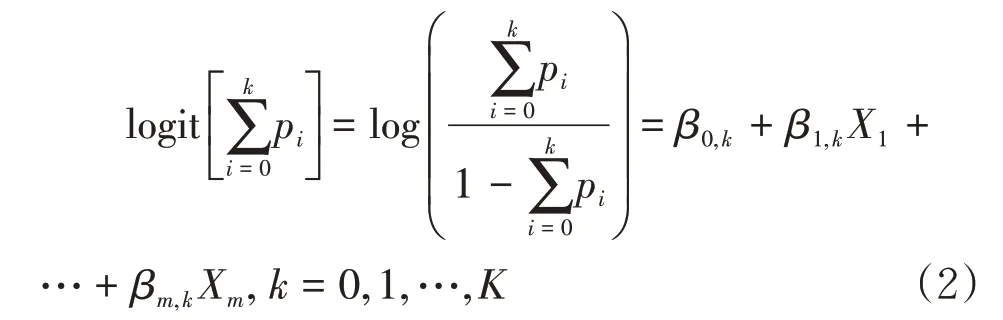
其中pi= Pr(Y=i|X)是索赔次数为i次的概率，K为索赔次数最大值。根据式（2），可以推出索赔k次的概率pk，即：

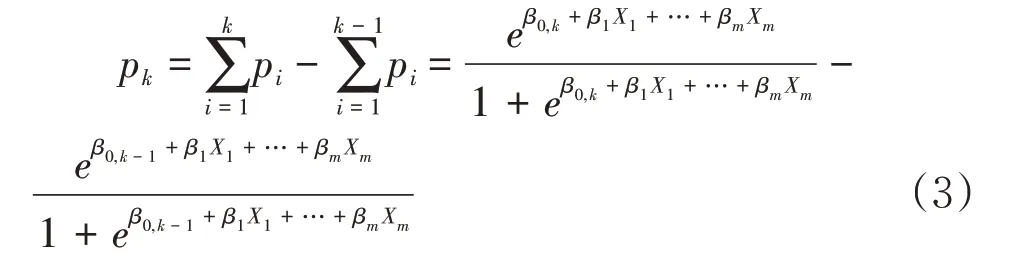
同时考虑概率的规范性约束：

Mccullagh（1980）［19］证明了当样本数n足够大时，极大似然法得到的有序模型是唯一确定的。将模型参数的估计值代入式（3）和（4），可以计算出不同索赔次数的发生概率。

Logistic模型的结果具有概率意义，驾驶员或车辆信息发生变化时，将引起索赔概率的变动，从而影响预期索赔频率。定义相对风险系数I来分析解释变量变动对预期索赔频率的影响，计算公式为：

其中xb为解释变量的基础类别。

（二）模型评价

为了客观评价OLR 模型的预测能力，将OLR模型与泊松模型（Poisson）、零膨胀泊松模型（ZIP）和零膨胀负二项模型（ZINB）相比较，选用相同的解释变量训练模型。由于这些模型之间不存在嵌套关系，赤池信息准则（AIC）、贝叶斯信息准则（BIC）和偏差（Deviance）等模型评价指标并不能客观地反映模型的优劣（Kuha，2004）［20］。另一方面，由于数据集本身的“零膨胀”特点，如果按照最小化贝叶斯误差来确定分类，那么所有驾驶员的索赔次数都将被预测为0次，所以比较预测的准确率也没有任何实际意义。

一个保险合同组中不同索赔次数的情况往往更值得关注，参考殷崔红等（2019）［11］使用的模型比较方法，本文选择卡方检验来评价模型对合同组的预测能力，卡方统计量定义为：

上式中，Oi为实际观测到索赔i次的样本数，Ei为索赔i次样本数的预测值。

三、实证分析

本文以国内2017年某车险数据为分析样本，包含172254 条有效数据①。原数据中包含索赔次数和17个解释变量，本文从泊松回归模型出发，根据AIC 准则，使用向前向后逐步回归，确定最终模型包含8 个解释变量，如表1。在使用OLR 模型时，本文将被解释变量索赔次数视为分类变量。

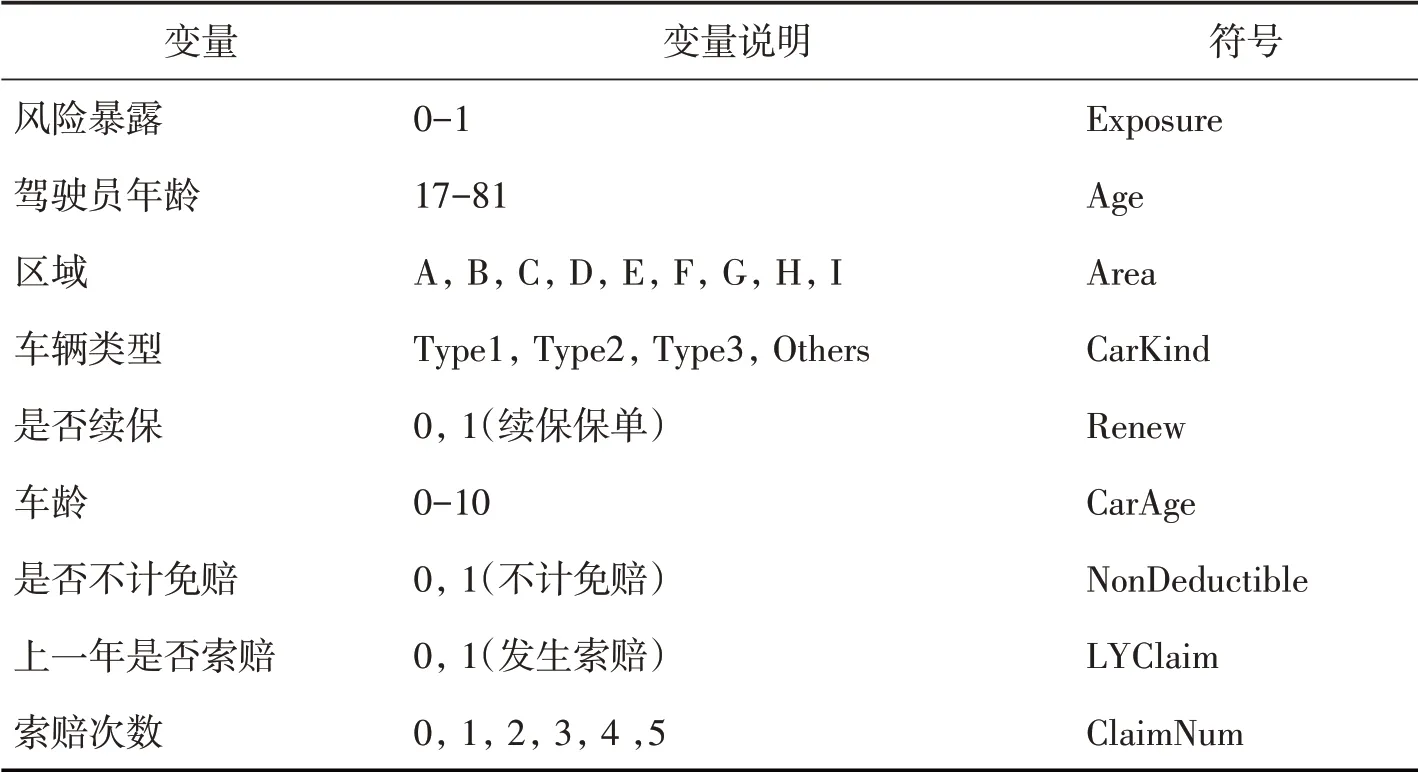
表1 变量符号及说明

连续变量描述统计如表2，分类变量频数统计如表3。

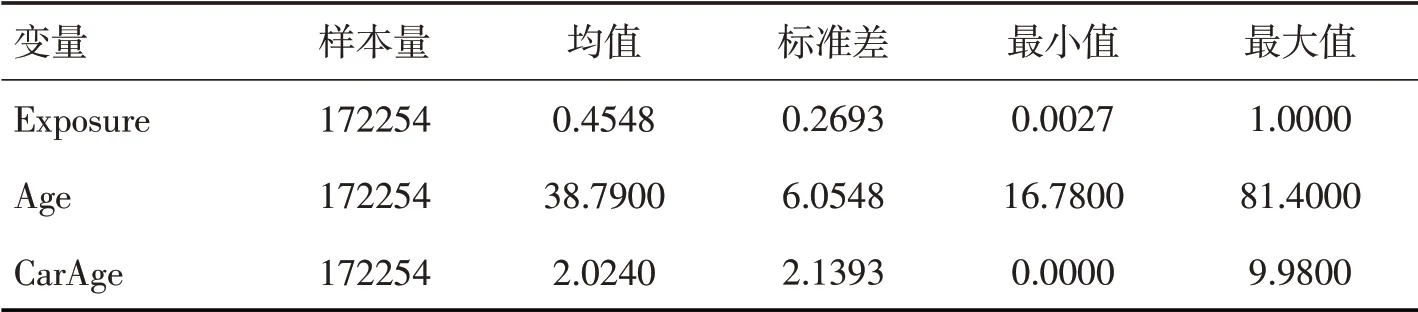
表2 连续变量描述统计

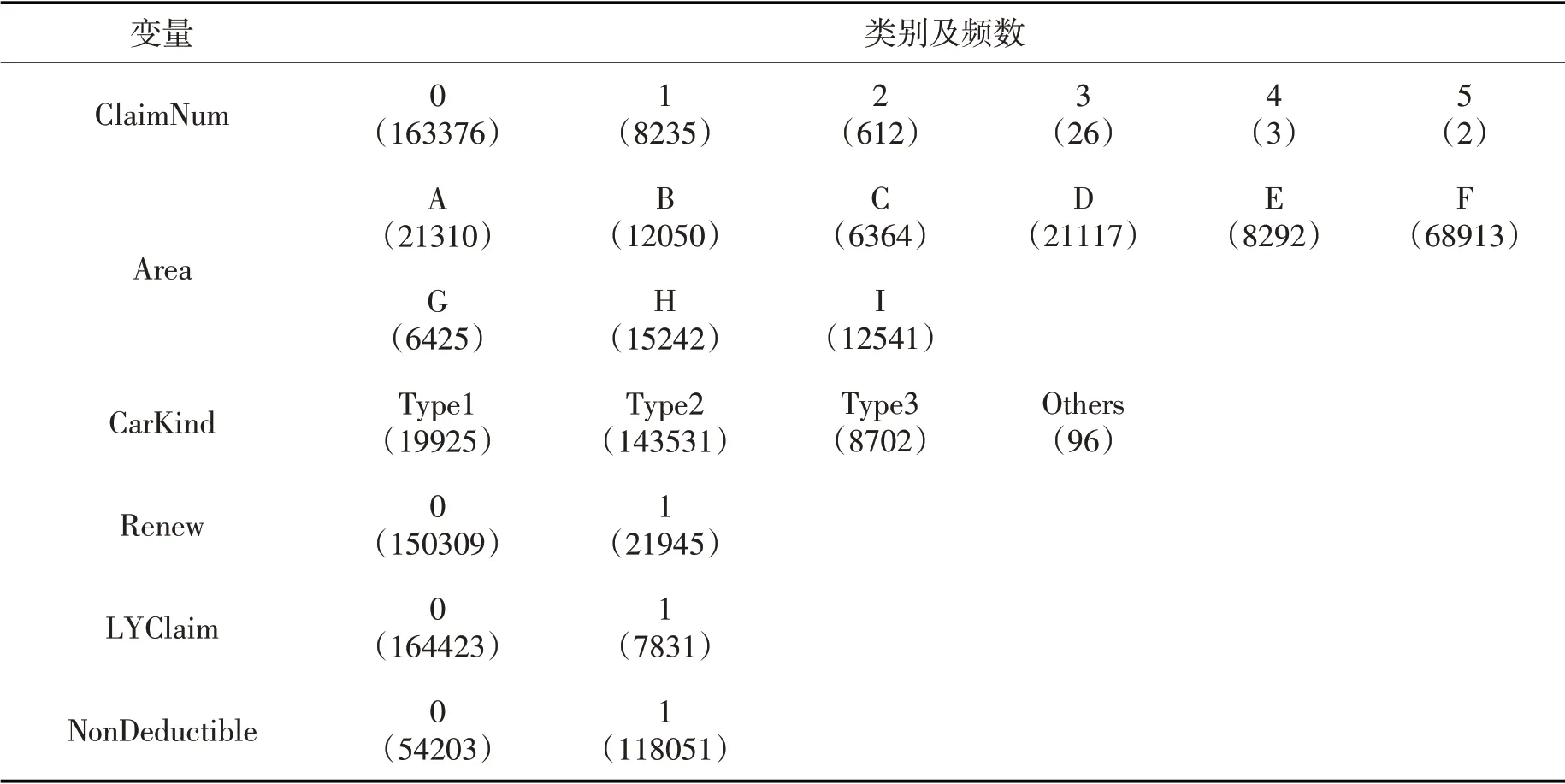
表3 分类变量频数统计

数据集中零次索赔的占比约为94.8%，索赔次数有明显的“零膨胀”特征。为了保证数据结构的一致性，本文根据索赔次数随机分层抽样，将样本数据分为训练集（70%，样本数为120578）和测试集（30%，样本数为51676）。

（一）模型估计

为了对比OLR 模型与泊松模型、ZIP 模型和ZINB模型的差异，所有模型使用相同的解释变量，差异仅为索赔次数的变量类型。本文将分类变量中频数最多的分类视为基础类别，使用R软件得到OLR模型极大似然估计结果，如表4。

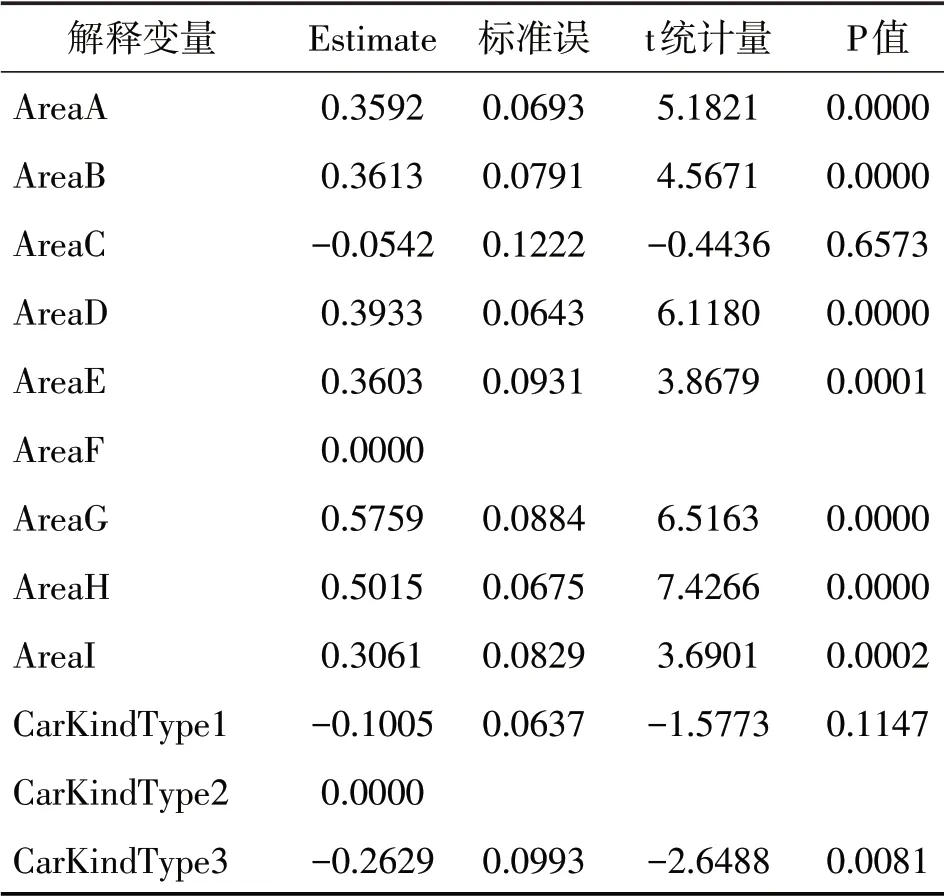
表4 极大似然估计结果（连接函数为Logit）

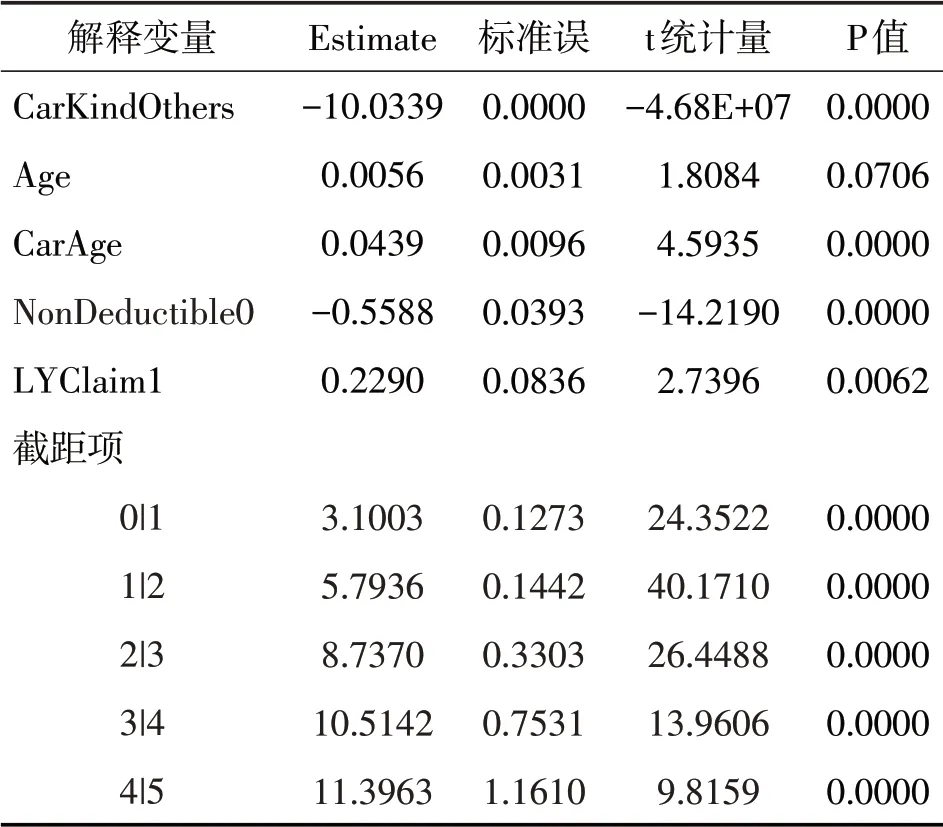
CarKindOthers Age CarAge NonDeductible0 LYClaim1截距项0|1 1|2 2|3 3|4 4|5-10.0339 0.0056 0.0439-0.5588 0.2290 3.1003 5.7936 8.7370 10.5142 11.3963 0.0000 0.0031 0.0096 0.0393 0.0836 0.1273 0.1442 0.3303 0.7531 1.1610-4.68E+07 1.8084 4.5935-14.2190 2.7396 24.3522 40.1710 26.4488 13.9606 9.8159 0.0000 0.0706 0.0000 0.0000 0.0062 0.0000 0.0000 0.0000 0.0000 0.0000解释变量Estimate 标准误 t统计量P值

使用似然比检验对整个模型进行检验，p值显著小于0.05，模型整体有意义，如表5。

表5 模型整体检验（原假设为模型仅包含截距项）

（二）模型评价

参考Agresti（2003）［17］对连接函数的讨论，本文分别选择Logit、Probit 和负双对数（Nloglog）三种连接函数建立OLR 模型，并与Poisson、ZIP 和ZINB模型相比较，索赔次数预测结果如表6。

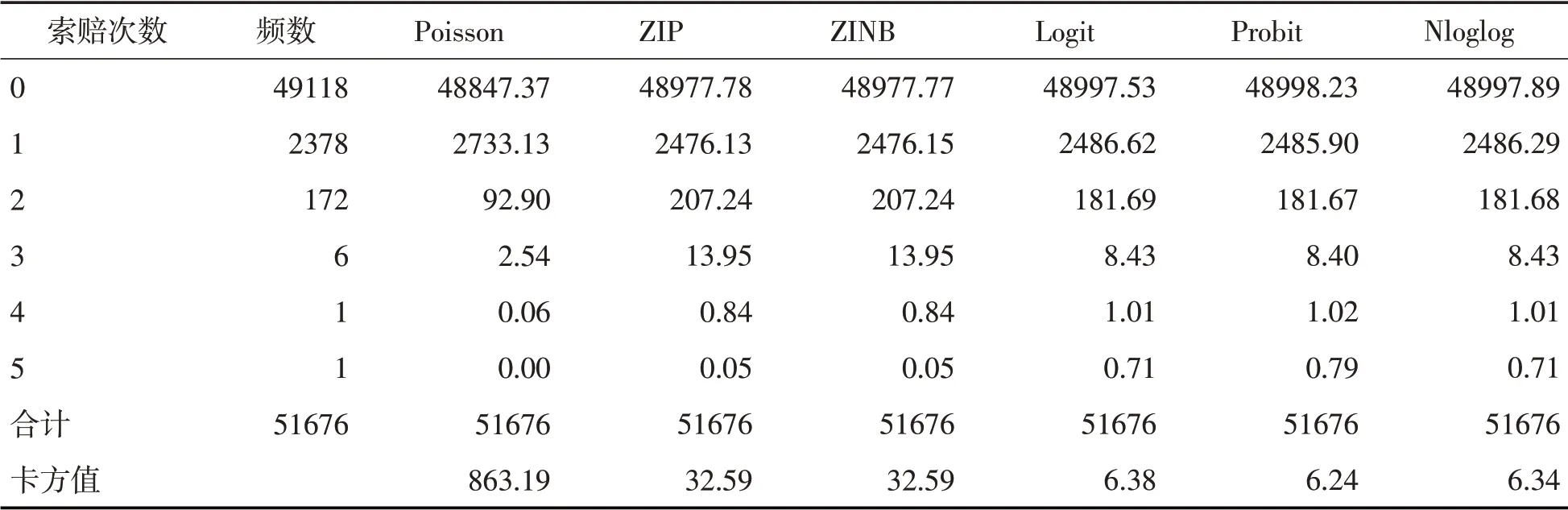
表6 测试集索赔次数预测结果比较

由表6可以发现，泊松模型完全未考虑数据中的零膨胀、过离散和异质性，其卡方值为863.19，显著高于其他5个模型，尾部概率的估计明显偏离实际值。ZIP 和ZINB 的卡方值非常接近，一定程度上解决了零膨胀问题，但是当索赔次数超过3 次后，预测效果明显降低。OLR模型的卡方值最小，并且对尾部风险的预测效果更好。其中，以Probit为连接函数的OLR 模型预测结果最优，但是三个OLR 模型的卡方值属于同一个量级，差异可能来源于随机性，所以无法在统计意义上确定哪一种连接函数的OLR模型更好。

估计索赔频率是车险精算建模的重要工作，因为广义线性模型的分析基于被解释变量的均值（王选鹤等，2018）［10］，所以不同模型对索赔频率的估计差异较小，如下表。

表7 测试集索赔频率估计及误差

OLR 模型整体上优于泊松模型和零膨胀模型，以Probit 为连接函数的OLR模型的误差最小，仅为0.002583。

（三）模型应用

不同连接函数的OLR 模型差异较小，本文选择更平滑且更常用的Logit 作为连接函数，进行下一步分析。按照OLR 模型的思路，分析某一变量对于不同索赔次数发生概率的影响，本文以车型（CarKind）为例，讨论不同车型索赔概率的差异。

固定其他条件不变，设定连续变量取值为平均值，分类变量取值为基础类别，计算不同车型的索赔概率，结果如图1。样本数据中，车型为Others的索赔次数全为0，所以图1中Others类别的车型0次索赔概率接近1，其他次数索赔几乎为0。

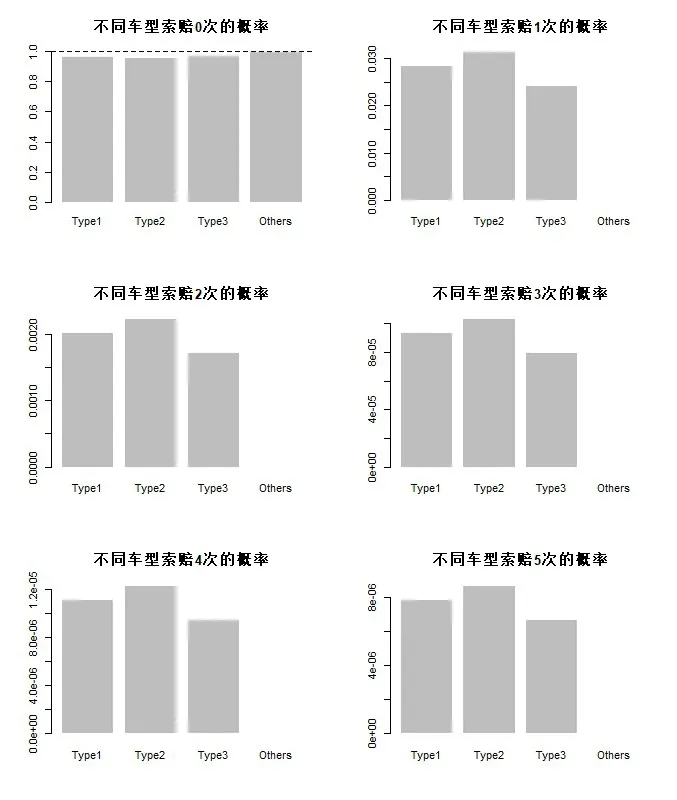
图1 不同车型索赔概率对比

由于Others 样本数仅为96，考虑到统计显著性，主要分析其他三种车型相对风险关系。在3种车型中Type2索赔的概率最高，而Type3发生索赔的概率最低。另外，索赔1-5 次的图形具有极高的相关性，在发生索赔的条件下，不同车型的相对风险关系是稳定的，也就是说索赔次数的大小，并没有影响解释变量与被解释变量之间的相关关系。使用相对风险系数I来评估不同车型对索赔频率的影响，结果如表8。

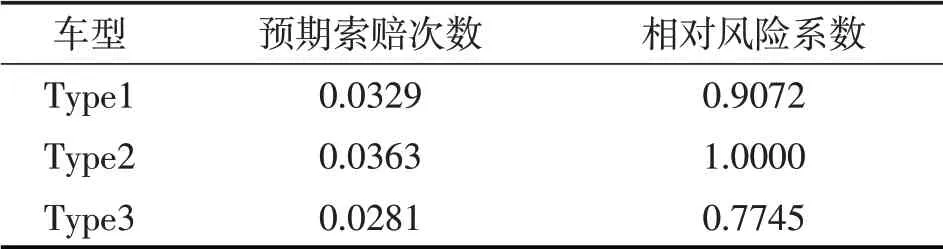
表8 不同车型相对风险系数

就这3 种车型而言，Type3 的相对风险系数为Type2 的0.7745 倍。如果仅考虑这一样本集的经验数据，在其他条件一样的情况下，Type3 车型保单的纯保费应为Type2的0.7745倍。类似地，可以根据不同投保人的特征计算对应的相对风险系数，为差异化定价提供参考。

四、小结

为解决车险索赔次数建模面临的零膨胀等一系列问题，本文选择了多元有序Logistic 回归模型，分别使用Logit、Probit和Nloglog三种连接函数建立OLR 模型，并与泊松模型、ZIP 模型和ZINB模型相比较。OLR模型解决了部分“零膨胀”带来的问题，该模型显著优于现有的泊松模型、ZIP 模型和ZINB模型，以Probit作为连接函数的OLR模型卡方值最小。特别是，OLR 模型克服了传统计数分布的限制，参数估计更灵活，对尾部概率的预测也更准确。但是不同连接函数的OLR模型的预测能力相近，卡方值的差异可能来源于随机因素，所以无法从统计意义上确定使用哪种连接函数的OLR模型更适合分析车险索赔次数。

在保险实务中，不同风险因素对索赔概率的影响是关注的重点，而模型的预测能力与解释性呈反比关系，现有的混合泊松模型已经开始面临参数解释性差的难题，复杂的混合分布让风险来源更加难以识别。OLR 模型不仅具有很好的预测能力，并且结果具有概率意义，所以较好的解释力是其与生俱来的优势。在解决“零膨胀”问题的基础上，OLR模型可以分析不同风险因素变动对索赔概率的影响。例如，本文对车型（CarKind）的分析，不同车型的相对风险系数可以作为车险定价的参考。另外，在模型应用过程中，当研究不同索赔次数的发生概率时，解释变量与索赔次数之间的相关关系是不变的。

上述结论证明OLR模型可以合理应用于承保核保等一系列环节，能帮助险企综合考虑人、车等多个因素，以实现风险识别，选择目标客户群体。

［注 释］

①本文的数据来自国内某财产保险公司2017年的机动车辆保险业务，车辆类型为货车。原数据共有173335 条保单数据，剔除了“赔付金额”为负的8 条数据和“NCD 满期基准保费”为负的1073 条数据，保留了172254 条有效数据。