基于VaR 风险度量准则的水产养殖保险最优风险分层测度
——以南美白对虾为例
郑 慧,王舒仪,于霄葳
(1.中国海洋大学经济学院,山东青岛266100;2.中国海洋大学海洋发展研究院,山东青岛266100;3.国家海洋信息中心,天津300171)
一、引言
我国的水产养殖总产量在2017年达6445.33万吨,占全世界总产量约70%,是名副其实的世界水产养殖大国[1]。但是水产养殖业很容易受到自然环境和气候变化的影响,历年来遭受的各类致灾损失也是惊人的。2019年8月,台风“利奇马”携带的狂风暴雨严重袭击了环渤海地区,东营港沿海有10 多万亩养殖场遭到破坏,仅黄骅南排河镇虾池受损面积就达47000亩。
为了应对水产养殖行业所遭受的自然风险,20世纪初英国、美国等发达国家便已建立起了洪水保险等针对灾害风险的保险制度。中国自2013年起,在原农业部和地方政府的支持下,也开始了水产养殖保险的试点,譬如福建省2017年推行的水产养殖台风指数保险,通过指数化台风的产品模式为养殖户提供保险赔偿,根据事先约定的台风区域和台风级别作为触发标准。

表1 福建省近年水产养殖台风指数保险承保情况统计表
但是我国当前水产养殖保险的推行比例甚至不足全国可保范围的5‰,远远低于全世界7%的平均水平[2]。水产养殖行业物种类别丰富以及生产环境特殊等状况导致了该类保险的成本高、风险高同时收益低的特点,诸多保险公司望而却步。在梳理国外部分国家保险发展历程中我们发现,再保险是现代保险经营的一项非常重要的风险分散机制。对保险人而言,再保险是为了将自身有可能遭受的风险控制在一个可控的范围,从而实现公司的稳定经营。水产养殖保险未来发展过程中的难题需要政府、监管机构、保险机构、互保机构和养殖户五个方面来共同解决。我国八部委曾发布《关于改进和加强海洋经济发展金融服务的指导意见》,并指出为了更好地推动“蓝色经济”的高质量发展,要积极推行巨灾保险和再保险机制。所以,面对我国水产养殖保险市场需求与承保能力不相匹配的问题,开发水产养殖再保险极为重要且紧迫,而最优分保点的确定是其中的关键所在。
二、文献综述
水产养殖保险公司面临的承保风险是当灾害发生后需要支付的赔偿。由于与其他农业保险种类相比水产养殖保险风险分布的研究文献比较少,所以借鉴对其他农业保险险种的研究拟合水产养殖保险风险分布。在现代农业保险风险分布的研究中,学者们最初将正态分布、指数分布、Exponen⁃tial 分布、Gamma 分布、Lognormal 分布、Weibull 分布作为农业保险风险分布的候选模型,取得良好效果。为了整体的拟合效果,一般采取剔除极端值的方法。但是随着农业风险损失经验数据的大量积累和计算机处理数据能力的不断提高,学者们发现边缘分布并不一定完全服从正态分布,于是在研究中逐步引进了极值分布和t 分布等分布函数(杨旭,2008)[3]。Fisher and Tippett(1928)[4]最早提出极值理论,并且通过分析,证明了极值极限分布的三大类型定理,奠定了未来极值理论发展的基础。Mikosch(1997)[5]运用极值理论探讨了巨灾损失情形下保险公司的破产概率和再保险问题。El⁃ing and Toplek(2009)[6]和王正文等(2014)[7]使用copula函数构造关于赔付额的联合分布模型,相较传统分布模型,copula函数模型能够突破变量间的相关性不随时间变化的假设限制,尤其适用于保险赔付受理赔次数和理赔额之间相关关系影响复杂的情形。但是,copula函数的拟合优度统计检验大多需要借助Kolmogorow-Smirnov 检验、Ander⁃son-Darling 检验和卡方检验等统计检验方法进行,而这些检验方法对于样本量都有很高的要求(李述山,2010)[8]。显然,对于水产养殖保险赔付额这种发展时间短,以年度数据为基础的承保业务而言,经验数据量难以满足要求。黄延信等(2013)[9]认为水产养殖保险不同于一般农业保险的地方就是其巨灾性,因此拟合水产养殖保险的风险分布,尤其是着重研究那些发生概率小但损失程度严重的风险。巨灾损失发生的概率较小,样本也较少,极值理论中的POT-GPD 模型恰恰可以解决传统研究方法中无法超越样本数据来开展分析的弊端。E.Brodin and H.Rootzen(2009)[10]等学者使用广义帕累托分布(GPD)对风暴、飓风保险损失评价中用于优化所使用的极值方法,使用具有厚尾性的损失分布模型来对巨灾风险进行定价。解强(2010)[11]引入贝叶斯统计中的马尔可夫蒙特卡洛(MCMC)方法来对POT 模型进行估计,拟合出我国因暴雨造成的损失分布。耿贵珍(2016)[12]利用POT-GPD模型研究了地震巨灾风险测度和地震巨灾损失分布,并且提供了三种阈值的取值方法。杨汭华和孙婧(2018)[13]利用POT-GPD 模型,对数据要求少,利用有限的数据研究极端损失以克服损失数据稀缺的优势来拟合农业保险大灾风险。何树红等(2019)[14]阐述了Bayes 混合分布模型的基本理论以及在我国农业旱灾风险度量中的运用,得出Norm-GPD 混合分布比Gamma-GPD混合分布拟合农业旱灾损失率分布效果更佳的结论,研究结果对于我国农业旱灾风险管理以及农业灾害保险、债券的定价具有重要的指导意义。极值理论对巨灾损失的尾部能够进行很好的拟合,已经有很多学者将极值理论应用于农业保险研究中,而水产养殖保险是农业保险的一种,因此我们可以借鉴农业保险将其应用于水产养殖保险风险的研究中,选用POT-GPD模型,拟合水产养殖保险风险的尾部分布。
在投保再保险时,原保险人最关注的是其自留风险和再保险费用之间的关系,他们希望自留风险和再保费都能达到最低,但是自留风险较低的情况下,其再保费必然会较高,因此如何确定最佳的分保点就成为了保险公司进行再保险时研究的重点(孙婧、杨汭华,2014)[15]。关于分保标准这一问题,以往的学者分别从破产理论(Bai and Guo,2008)[16]、均值-方差模型(Li and Li,2013)[17]、效用理论(Yuen et al,2015)[18]等不同角度展开了详细的研究,使得最优再保险理论的研究成果得到了完善。Krokhmal and Palmquist(2002)[19]将VaR 引入最优再保险理论研究,VaR 测算在正常的市场波动与置信度下保险公司最大可能的损失,考虑了投资者对风险的真实感受,弥补了以上方法目标单一的不足,而且具有计算简单、可以计算组合风险等优点。Lu et al.(2013)[20]在停止损失函数呈现凸型的前提下,利用VaR 和CTE 最优原则来进行研究,最终发现基于VaR 的最佳再保险方式都是成数再保险,基于CTE 最优原则的最佳再保险方式是完全再保险。
从已有文献来看,大多数学者都已意识到水产养殖保险不同于一般农业保险的地方在于其巨灾性,并且分散巨灾风险的有效途径是完善再保险制度,再保险可以加强抵御巨灾风险的能力,在更大范围内分散风险,但是没有对水产养殖保险的巨灾分布和如何实现最优分保问题进行深入研究。本文利用极值理论深入研究巨灾风险的分布,从原保险人的角度出发基于VaR风险度量准则探究最优分保问题。
三、水产养殖保险最优分保比例测度的理论模型
本文从原保险人立场出发,建立水产养殖保险成数再保险的最优分层模型,计算最优自留比例。第一步,拟合水产养殖保险的风险分布,尤其是着重研究那些发生概率小但损失程度严重的风险,并且选用对于数据数量要求比较低的POT模型对风险的尾部分布进行拟合,弥补水产养殖巨灾损失的数据缺陷;第二步,确定成数再保险方式,完成对再保险保费及总成本费用的设定;第三步,结合VaR风险度量方法计算不同地区、不同时期等不同情景下的水产养殖保险最优再保险的自留比例,并对不同情境下保险公司所能选择的最优再保险给出建设性的意见。
(一)用POT-GPD模型构建边缘分布
设X1,X2,...,Xn是独立同分布的随机变量,分布函数为F(x),X0是F(x)的右端点,记为:X0=sup{x∈R,F(x)≺1}。μ表示阈值,设超过阈值μ的样本个数为Nμ,则Xμ+1,Xμ+2,...,Xμ+Nμ表示超过阈值的样本观测值。所以样本超额值Y 可表示为:Yi=Xi-μ,i=μ,μ+ 1,...,μ+Nμ,则超过某一阈值μ的超额值Yi的条件分布函数为:
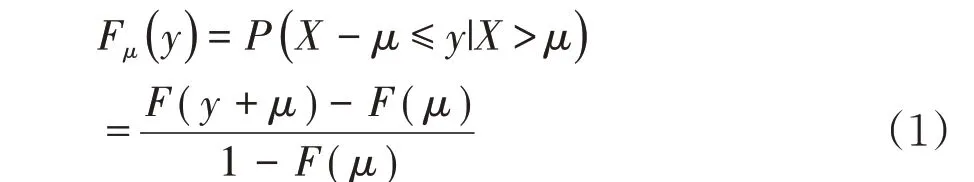
于是有
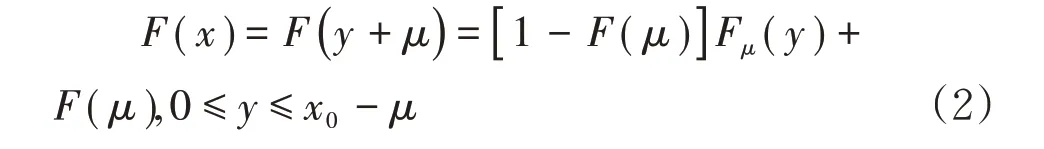
由Pickands-Balkame-De Haan 定理可知,对充分大的阈值μ,分布函数近似服从于广义帕累托分布(GPD)。则ξ≠0。通常式(1)中的F(μ)可以用经验分布来估计,最终得到:
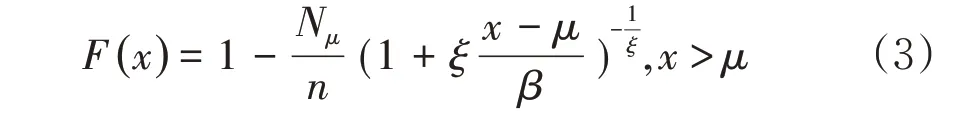
其中,ξ是分布的形状参数,β是分布的尺度参数。
(二)成数再保险成本费用设定
假设X是原保险公司面临的水产养殖保险赔付风险,β为原保险公司的自留比例,XL是原保险公司的自留风险,XR是原保险公司的分出风险,原保险公司总费用为T,再保险保费为δ(XR),政府给予水产养殖再保险保费的补贴比例为θ。X的累积分布函数为FX(x)=Pr{X≤x},生存函数为SX(x)=Pr{X>x}。
原保险公司的总成本为:
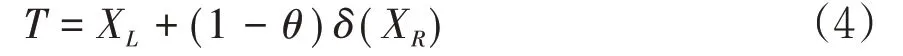
采用方差原理计算再保费为:
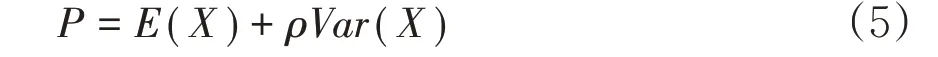
其中,P 是再保险保费,E(X)为风险的期望值,Var(X)为风险的方差,ρ为保费附加因子。
(三)VaR风险度量准则下的最优分保比例
成数再保险中,对于原保险人来说,给定置信水平时,总成本费用最低时的VaR 值为最优分保点。在VaR风险度量准则下,给定了置信水平1-α (0 <α <1),可以通过VaRT(β*,α)=来确定最优自留比β*。β*即为成数再保险下最优的VaR分保比例为:
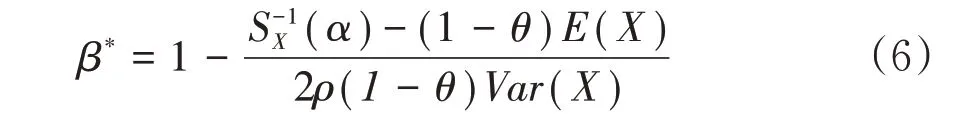
要使β*有意义,需满足β*>0,也就是1 -且,即得到VaR 准则下的最优自留比例β*存在的充要条件是0<。
四、水产养殖保险最优分保比例实证计算——以南美白对虾为例
(一)南美白对虾保险赔付率测算
本文采用2003-2017年《渔业统计年鉴》中南美白对虾养殖面积、单位面积产量、水产养殖面积、水产养殖成灾面积等统计指标和中国太平洋财产保险股份有限公司与安信农业保险股份有限公司保险条款中的水产养殖南美白对虾条款相关参数(保险金额4000 元,费率8%,保费320 元)作为南美白对虾保险赔付率测算的依据。同时,结合我国目前已有的南美白对虾保险条款,做出以下研究假设。
假设1:海水养殖风险空间分布均匀,也就是在所有的养殖区域内,风险发生的概率是一样的。
假设2:保险公司从育苗期开始承保。水产养殖分为育苗期、成长期和成熟期,保险条款中对每个时期的保障水平会有不同的规定,假设保险公司从养殖初期开始承保,则水产养殖过程中发生的所有损失都在保险责任范围内。
假设3:假设损失程度可能有两种,分别是60%和80%。参考农业保险参保物的极端损失程度,以单产损失60%作为巨灾损失的最低限,以单产损失80%作为特大灾的考察值。
假设4:设定三个承保率:5‰、7%和70%。当前我国保险机构承保的水产养殖面积大约为全国总水产养殖面积的5‰,世界平均承保率为7%,而农业保险的覆盖率为70%。
根据以上假设我们可以测算不同情景下的南美白对虾保险赔付率:

从上式可以看出赔付率主要跟赔付比例、损失程度受灾面积、保险金额以及单位保费有关,不同月份赔付比例如表2所示,并且通过以上假设我们可以得到多个情景,由于每种情景下的计算方法一样,我们可以以“养殖的第二个月份发生保险事故,损失程度达60%”(简记为60%-60%)为例进行分析:

表2 不同月份的损失赔付比例
南美白对虾保险赔付率=(水产养殖受灾率×4000×60%×60%)/320
(二)赔付率数据的厚尾性分析
在构建POT 模型之前,首先需要对南美白对虾保险赔付率数据进行厚尾性检验。实证中,我们通常将比指数分布的尾部更厚的分布定义为厚尾分布,即:由图1可知,南美白对虾赔付率数据的分布明显不同于正态分布,具有尖峰厚尾的特点。从图2 可以看出,赔付率数据的指数Q-Q图的尾部呈现出上凸的形状。因此,可以判定南美白对虾保险赔付率数据具有厚尾性的特征。
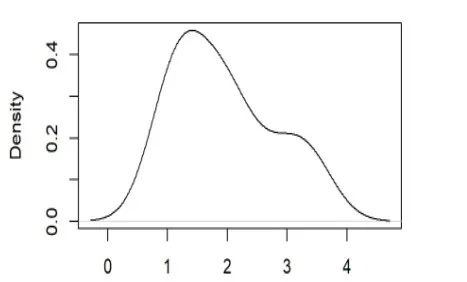
图1 南美白对虾保险赔付率的概率密度图
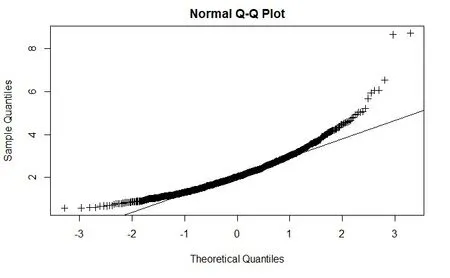
图2 南美白对虾保险赔付率的Q-Q图
(三)赔付率的分布拟合
我们以农业保险中常用分布模型为参考,选择Gamma 分布、Weibull分布和Lnorm分布作为候选分布,分别拟合不同情景下的南美白对虾保险赔付率的分布,结果如表3。通过比较我们发现,该情境下对数正态分布(Lnorm)的经验分布与理论分布的拟合偏差最小,为最适合南美白对虾保险赔付率分布的模型。Lnorm 分布为:若X 是一个随机变量,Y=ln(X)服从正态分布:Y=ln(X)~N(μ,σ2),则称X 服从对数正态分布。对数正态分布的概率密度函数:

表3 “60%-60%”情境下不同分布参数拟合表
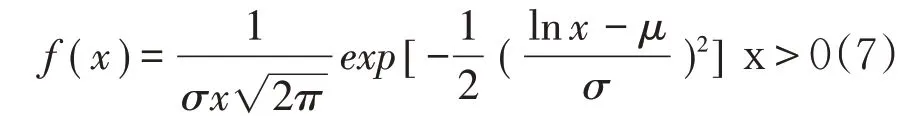
参数μ和σ分别是对数均值和对数标准差。当南美白对虾损失率为60%、赔付比例为60%时,经估计,μ=0.6989796,σ=0.4071648。

表4 “60%-60%”情境下赔付率分布的统计检验
(四)阈值μ选取与参数估计
由上节分析可知对数正态分布对南美白对虾保险损失率的拟合效果最好。为弥补赔付率巨灾损失数据的不足,我们以对数正态分布作为随机抽样发生器进行1000 次蒙特卡洛随机模拟,作为数据的扩充。
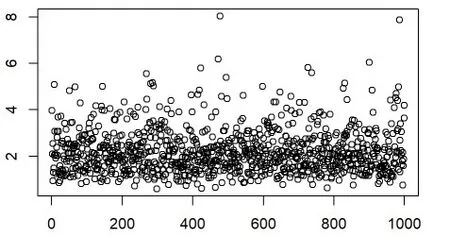
图3 1000次蒙特卡洛模拟产生的损失率数据的散点图
POT-GPD 分布实质上是对超过阈值μ 以上的Nμ个统计量进行研究。阈值μ的选择过大或过小都会导致参数估计结果的不准确。因此,合理地选取μ成为建立POT-GPD模型的关键。阈值的选取方法有多种,不同方法得到的阈值有较大差异,然而,时至今日到底选用哪种方法计算阈值,学术界并无统一定论。在实际应用中,常用平均超出函数图法(MEF图)结合剩余观测值的数量等问题来选阈值。一般地,通过观察MEF 图中曲线斜率的变化来确定阈值,将曲线斜率中存在明显变化的部分作为阈值,继而对超过阈值的部分来拟合GPD 分布。从图4 可以看出,曲线斜率在1.5 到2的中间出现了明显变化,结合剩余观测值的数量,最终选择1.7为阈值。

图4 MEF函数图
(五)POT-GPD模型的参数估计及检验
当阈值确定后,利用极大似然估计可以得到POT-GPD模型中参数ξ和σ的值。

表5 POT-GPD模型的参数估计
当阈值选择为1.7 时,结果如图5,其中,P-P图反映的是各变量累积概率与其对应分布的累积概率之间的趋势关系,Q-Q图反映的是所有数据变量分布的分位数和其对应分布的分位数之间的趋势关系,如果P-P 图和Q-Q 图上的所有点近似在一条直线上,则所选数据满足广义帕累托分布;DP图为尾部密度曲线的估计和直方图,重现水平图反映重现期的对数数据与其对应的重现水平之间的关系,如图中所示,所选的样本数据落在了指定分布的分位数置信区间内部,则可以认为所选取的数据符合广义帕累托分布。通过以上四个分布拟合诊断图看出,各数据点基本上分布在其参考线两侧,证明了对海水养殖南美白对虾保险风险利用POT-GPD是合理的。
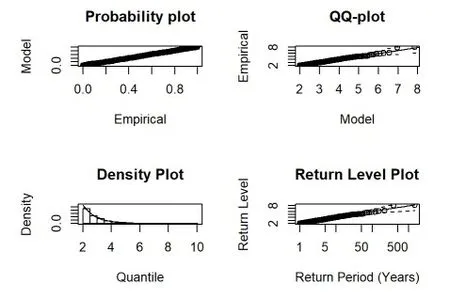
图5 GPD模型检验图
五、基于VaR 风险度量准则的最优分保结果分析
风险价值VaR是指在一定时间和一定置信度内的潜在最大损失,一般可以定义为:VaRp(X)=F-1(P)=inf{x∈R:F(x)≥P},0 于是,对于给定的置信水平P,风险价值VaRp就是损失分布的P分位数,其估计式为: 表6 “60% - 60%”情境下的最优分保结果 我们假定保险公司的风险容忍度为α=10%,费率附加因子ρ=0.2,政府对农业再保险保费的补贴比例θ=40%,用计算南美白对虾保险的最优自留比例。 将阈值与“最优分保”结合进行风险分层考虑则更具风险管理的稳健性。在“最优分保”的测算式中,最优分保比例的决定因素有保险人的风险容忍度(α)、再保险保费附加因子(ρ)、再保险保费补贴(θ)。当α、θ一定时,ρ越小,风险自留比例越低;ρ越大,风险自留比例越高。当ρ、θ一定时,α越小,风险自留比例越高。θ 越大表示保险人愿意分出更多的保险责任,这体现了再保险政策的激励性。当α、ρ、θ 确定时,最优分保的结果取决于承保率、保障水平和受灾程度等。当其他因素相同时,随着承保率的提高,自留比例随之提高;当其他因素相同时,随着保障水平提高,自留比例也提高;当其他因素相同时,水产养殖损失程度越高,自留比例越高,反之越小。 本文站在原保险人的角度,在追求自留风险损失最小化的基础上探讨成数再保险的分保最优决策,从而得到如下结论: 第一,在VaR 风险度量准则下成数再保险的分保最优自留比例易于判断,并且其结论在现实中的实用性比较强。由最优再保险的测算式可以得知,在已有风险分布模型中,影响保险公司最优自留比例的因素包含保费补贴比例(θ)、保险人的风险容忍度(α)和保费附加因子(ρ)。并且,保费补贴比例(θ)越大,保险人越倾向于分出更多的风险责任,这也佐证了渔业保险的财政扶持和激励政策是有效的。 第二,实务中可以将阈值作为风险分层的重要警示点,结合原保险公司的风险承受能力来确定自留风险即最优分保问题。但是,阈值点的选择受很多因素的影响,既有模型方面的因素,也有环境因素。例如,险种差异、地理位置的差异、时间节点的差异、保险公司风险态度的差异,以及假设条件、风险分布模型、统计检验准则的不同,都会造成阈值点的变化。因此,在实务中必须结合各个因素不断完善和修正分保比例的理论模型。 第三,赔付率数据是我们进行分析的基础,由赔付率计算公式可以看出赔付率与水产养殖受灾率、单位保额、赔付比例以及损失程度有关,与养殖面积、承保率无关,这些数据的质量对于选择恰当的风险分布模型具有重要影响。而现实中水产养殖保险实际灾害损失数据积累不足,我们只能用目前能够获取的数据做拟合,然后利用软件作扩充,虽然这不是损失率的理想表达,但本文理论意义要大于其在保险实务中的意义。 [注 释] ①由于协会未公布2020年单独年度数据,所以表中省略2020年数据,且2021年数据为截至2021年5月数据。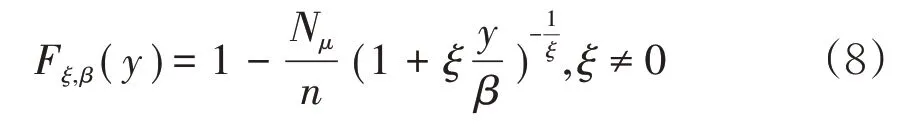
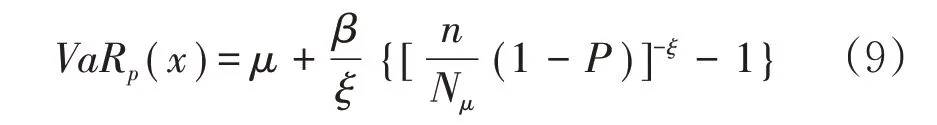

六、结论

