侧限压缩过程中散体矸石变形及破碎特征研究

肖 博，李永亮，李 进，王宇轩，王梓旭

(1.中国矿业大学(北京)力学与建筑工程学院，北京 100083；2.中国矿业大学(北京)能源与矿业学院，北京 100083)

0 引 言

固体充填开采是一种以固体混合材料作为充填承压结构的绿色矿山开采技术，其中的骨料多采用各种粒径复合的矸石[1-2]。矸石属于散粒体材料，原生级配较差，孔隙率高，利用其进行固体充填时易产生较大的压缩量，充填率低，充填效果较差。矸石在压缩过程中，内部颗粒会发生破碎，进而影响充填体的抗变形能力。因此，有必要对散体矸石压缩变形、孔隙率和破碎程度三者之间的内在联系展开研究[3]，掌握孔隙率和破碎程度对压缩变形的影响规律，进而优化固体充填骨料配比，提高充填体抗变形性能。此外，当散体矸石进入采空区成为充填体时，水平方向由于受到围岩和支护结构极强的约束作用，几乎不发生变形，垂直方向在上覆岩层的重力作用下，变形较为明显，因此散体矸石在侧限压缩过程中的变形特性在工程实践中受到了更多的关注[4]。

目前，已有较多学者对散体矸石的压实特性和破碎特性展开了研究。肖猛等[5]研究了粒径级配、加载速率对散体矸石压实特性和侧压系数的影响规律，并确定了试样的颗粒流细观参数；Pappas和Mark[6]对采空区垮落岩块的压实特性进行了研究，并采用Salamon和Terzaghi公式表征碎石的应力-应变关系；马丹等[7]对侧限压缩下破碎矸石渗透特性的研究中发现孔隙率随着压缩位移的增加而减小，较小颗粒充填到较大颗粒的孔隙中，是混合粒径试样初始孔隙率减小的主要原因；李建平等[8]利用冲击式破碎装置对矸石的冲击破碎粒度分布特性进行了研究，矸石的冲击破碎粒度符合Weibull分布，随着冲击速度的增加，矸石破碎程度减小；辛恒奇等[9]通过侧限压缩试验与声发射试验，对侧限压缩条件下同级配、不同岩性的散体矸石在不同压缩阶段的声发射特征进行了研究；Zhou等[10]采用SANS试验机与自制钢筒，以粒径大小、加载速率和初始加载应力为试验变量，研究了矸石的能量耗散规律与压实变形特性。上述以散体矸石为主要研究对象的试验及理论分析中，主要是研究散体矸石在压缩过程中某个单一特性的变化规律，关于孔隙率和破碎程度对矸石压缩变形的综合影响机理则研究较少，且缺少试验分析和理论推导相结合的研究过程，因此对此展开系统的研究是非常有必要的。

本文采用加载装置和声发射监测设备相结合的试验系统，结合试验数据和理论计算，对侧限压缩过程中散体矸石的变形及破碎程度特征进行了研究，进一步揭示了散体矸石产生宏观变形的机理，不同加载速率条件下的试验结果可为固体充填开采设计提供理论参考依据，具有较强的工程实际应用价值。

1 实 验

1.1 试验设备系统

试验设备系统分为加载控制系统和声发射监测系统两部分(见图1(a))。加载控制系统采用YAD-2000微机控制电液伺服压力机，可加载的最大试验力为2 000 kN，采用控制速率的加载方式，初始试验力为1 kN。为便于装卸试验材料，根据内径与散料最大粒径之比不小于5 ∶1的原则，设计钢筒内径为150 mm，适用于最大粒径等于30 mm的侧限压缩试验。钢筒材质为40# 优质碳素结构钢，强度较高，不易变形，最大装料高度为260 mm。

图1 试验系统Fig.1 Testing system

声发射监测系统主要由显示器、主机和传感器三部分组成。选用4个RS-54A传感器对散体矸石试样进行定位，为保证良好的三维定位效果且传感器位置不高于试样的变化高度，需将4个传感器分别布置在钢筒外侧前后左右4个方位的中下部，具体位置分别为左1和右2(钢筒高度的1/2处)，前3和后4(钢筒高度1/4处)(见图1(b))。为使钢筒与传感器能够充分接触耦合，需提前用AB胶固定好传感器夹具，并在接触部位涂抹凡士林。根据放大器参数及参考文献，确定声音门槛值为40 dB，进而减少试验环境中的噪音以免对声发射监测结果造成干扰。试验过程中，先启动加载装置，待其出现稳定数值后再启动声发射装置，试样发出的声音信号通过传感器探头接入，再通过放大器扩大信号后传出，导入主机(见图1(c))，系统自动记录相关参数随时间的变化过程[11-12]。

1.2 试验材料

1.2.1 矸石原材料

各种粒径的矸石取自察哈素煤矿，使用国家标准分级筛挑出大于30 mm的矸石后，将30 mm以内的矸石通过20 mm、15 mm、10 mm和5 mm四个次级分级筛进行粒径分组(见图2)。试验时，将混合均匀的散体矸石，分5次倒入钢筒内，每装料一次，需用活塞对其进行表面平整，以降低装料造成的孔隙率误差。

图2 各种粒径的矸石Fig.2 Gangues of various particle sizes

1.2.2 矸石的微观结构

用电镜扫描散体矸石粉末的局部微观形貌，得到不同倍数下的散体矸石SEM照片(见图3)。低倍数的SEM照片(见图3(a)、(b))显示：散体矸石粒度大小不一，颗粒之间分布松散，孔隙较为发育，细小颗粒填充粗颗粒，但存在变形空间，可压缩性大。高倍数的SEM照片(图3(c)、(d))显示：矸石颗粒为形状不规则的块体结构，多棱多角，颗粒本身较为致密，大颗粒表面附有碎屑式的鳞片结构，整体磨圆性较差，具有一定的质感[13-14]。

图3 不同倍数下的散体矸石SEM照片Fig.3 SEM images of granular gangue in different multiples

1.3 试验方案

泰波理论在散体颗粒级配优化方面应用较为广泛[15]：

(1)

式中:P为散体各粒径的通过百分率，%；d为散体中的各粒径，mm；D为散体的最大粒径，mm；n为级配系数。试验选定D=30 mm，n=0.3泰波级配组，由泰波理论计算出各粒径范围颗粒的含量：11%(20～30 mm)、8%(15～20 mm)、9%(10～15 mm)、14%(5～10 mm)和58%(0～5 mm)。

为研究不同加载速率(v)对矸石破碎变形的影响，分别以v=0.5 kN/s、v=1.0 kN/s、v=1.5 kN/s和v=2.0 kN/s四种加载速率对上述级配组进行单轴侧限压缩，最大试验力为10 MPa。

2 矸石孔隙率变化特征

2.1 应力-应变关系

加载速率影响下的应力-应变(σ-ε)关系如图4所示，随着加载速率v值的增加，应变逐渐增大，即抗变形能力随v值增大而减弱。分析其原因，级配组合和最大试验力都保持不变时，v越大，加载时间就越短，试验力快速增大，较高的应力水平对孔隙的压缩效果更为强烈，从而导致试样的宏观变形更大。

图4 应力-应变关系曲线Fig.4 σ-ε relationship curves

在侧限压缩过程中，应力随着应变呈指数型增长，对曲线进行非线性拟合，关系式列于表1。整个压缩过程可以分为三个变形阶段：0～2 MPa为快速压缩阶段，该阶段内的变形主要来源于轴向应力对试样初始孔隙的直接压缩，变形量占到总体的50%以上；2～4 MPa为平稳破碎阶段，变形的主要来源由对孔隙的直接压缩转变为粒径破碎后对孔隙的二次填充，试样的破碎主要发生在这一阶段，变形量占到总体的25%左右；4～10 MPa为缓慢压实阶段，试样逐渐被压密且破碎程度越来越小，直至不再发生破碎。对比前两个阶段可知，散体矸石试样宏观变形的主要来源是内部孔隙被压缩和填充，其中低应力状态下对孔隙的直接压缩最为明显。

表1 应力-应变曲线拟合情况Table 1 σ-ε curves fitting situation

2.2 孔隙率-应变关系

矸石为粒度均匀、形状不规则的散粒体材料，其孔隙率K的公式为：

(2)

式中：V为松散状态下矸石的表观体积，mL；V0为矸石在绝对密实状态下的绝对体积，mL。由于压实钢筒内部矸石的绝对体积无法直接测量，故先对试验用矸石的绝对密度(ρ0)进行测定。

首先用量程为1 000 mL的量杯称量适量的水，记录体积读数V1k(k为矸石绝对密度测定试验次数，下同)，将量杯和水一起放至在精度为0.001 kg的电子秤上称重，记录质量读数m1k；然后往量杯中加入适量的矸石，使其完全浸没在水中，静置一段时间，待杯壁水滴充分下流，且不再有气泡产生后，记录量杯内稳定的液面读数V2k，并再次称量总体质量，记为m2k。

为保证试验的准确性，上述称量过程重复10次，表2为矸石绝对密度测算试验数据，根据表2中记录的数值计算得到的矸石绝对密度为：

表2 矸石绝对密度测算试验数据Table 2 Calculation test data of gangue absolute density

(3)

设钢筒内部半径为r，压缩后矸石的剩余高度为h，压缩前后矸石质量m保持不变，则有：

V=πr2h

(4)

(5)

联立计算式(2)～(5)可得：

(6)

由式(6)可知，当质量和钢筒内径一定时，压缩过程中孔隙率会随着矸石剩余高度的减小而减小。

设矸石初始装料高度为h0，则矸石试样在压缩过程中的应变为：

(7)

由式(6)和(7)可得：

(8)

由此可以得出，在给定h0的情况下，孔隙率随着应变的增大而逐渐减小。当ε=0时，可以得出，初始孔隙率与初始装料高度呈正相关。

2.3 孔隙率-应力关系

根据式(6)可计算出不同应力对应的孔隙率大小，孔隙率随应力的变化如图5所示，随着应力不断增大，孔隙率阶段性减小，其中，0～2 MPa范围内速率较大，2～4 MPa时次之，4～10 MPa内最为缓慢，这与宏观变形的三个阶段是相互对应的。由于级配组合D=30 mm，n=0.3保持不变，故初始孔隙率相同，此后随着加载速率增大，孔隙率在各应力阶段下降越快，说明速率越大，孔隙率变化量越大。

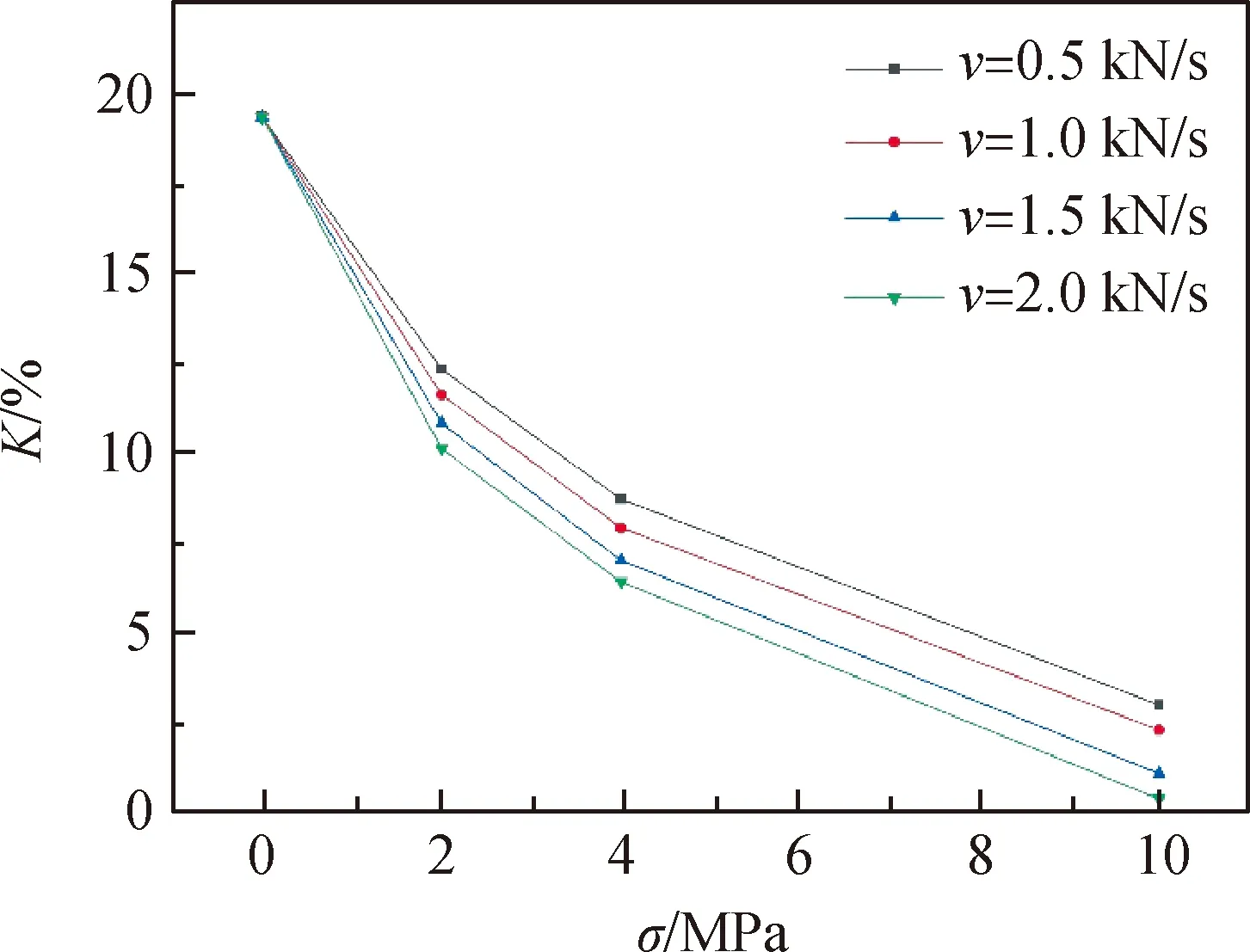
图5 孔隙率-应力关系曲线Fig.5 K-σ relationship curves

另外，表1中的拟合关系式可用式(9)表示：

ε=a+bln(σ+c)

(9)

将式(9)代入式(8)可得孔隙率K与应力σ的关系式：

(10)

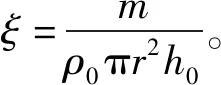
3 散体矸石破碎特征

3.1 散体矸石破碎分形特征

根据分形的基本定义，如果颗粒粒径分布具有分形特征，则粒径分布可以用幂律形式[16-17]表示：

N(x)=Ax-α

(11)

式中：N(x)为粒径大于x的颗粒数目；A为比例常数；α为粒径分形维数，α越大，碎块越多，粒度越小，破碎越严重。

对式(11)进行微分可以得到破碎颗粒的粒径密度分布函数：

dN(x)=-αAx-α-1dx

(12)

将颗粒的质量M(x)和M(D)用对应的颗粒粒径来表示:

M(x)=Bρ0x3

(13)

M(D)=Bρ0D3

(14)

式中：B为颗粒的体积形状系数。

根据式(12)和式(13)，粒径小于x的累计质量可以表示为：

(15)

由式(14)和式(15)可得全部粒径表示的总质量：

(16)

联立式(15)和式(16)可得小于x的粒径通过率P为：

(17)

对式(17)进行对数变换，得到对数坐标下的散体矸石破碎分形函数：

(18)

式(18)为颗粒粒径小于x的质量累计概率分布函数，如果矸石的破碎粒径具有分形特征，颗粒的质量累积概率和粒径比值在对数坐标中作图，斜率为3-α，即斜率越小，α值越大，破碎程度越大[18-19]。

将压缩后的矸石进行重新筛分，得到破碎后各粒径范围矸石颗粒的含量，再结合函数(18)绘制出双对数坐标曲线(见图6)，并对其进行拟合得出斜率大小，对比分析粒径的破碎程度。

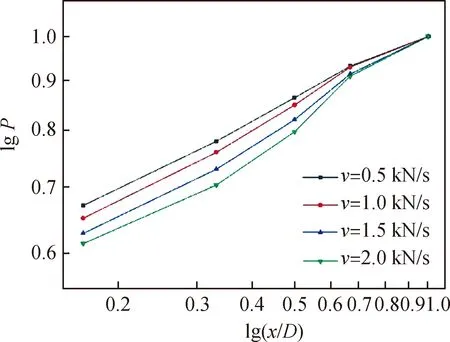
图6 矸石破碎分形曲线Fig.6 Breakage fractal curves of gangue

双对数坐标系中破碎分形曲线的拟合情况如表3所示。v值越大，拟合曲线的斜率越大，粒径分形维数越小，即破碎程度越小。分析原因：加载速率较低时，矸石试样内部的大小颗粒有充分的时间调整和磨合，颗粒之间的接触面积和接触程度越来越大，从而导致破碎程度较大；加载速率较高时，试样内部的位置来不及充分调整，颗粒之间的接触多为大粒径矸石的相互搭接，小粒径矸石受压程度较小，从而导致破碎程度较小，而且，加载速率越大，短时间内被初始孔隙所吸收的能量越多，用于破碎的能量越少。

表3 双对数曲线拟合情况Table 3 Double-logarithmic curves fitting situation

综上，颗粒的破碎程度越大，对孔隙的二次填充率越高，孔隙不容易被进一步压缩，试样抗变形能力增强。

3.2 声发射(AE)定位特征

声发射系统可以监测到试样的AE定位情况，进而确定散体矸石内部发生损伤和破碎的具体位置。钢筒外侧布置的4个传感器到声源的距离一般不同，因此会产生时差定位，通过显示器可以直接观察到矸石发生破碎的发展程度和具体数量。

不同试验条件下矸石侧限压缩过程中的AE定位数变化规律相似，AE定位数随着试验力的增大而不断增加，不同变形阶段定位点数相差较大。0～2 MPa阶段内，试样发生快速压缩变形，定位点较为稀疏，说明该阶段以压缩初始孔隙为主，颗粒间主要以摩擦的形式相互接触，破碎程度微弱，可监测信号较少。2～4 MPa阶段内，试样发生平稳破碎变形，定位点数快速增长，说明有大量的破碎事件发生，颗度较大的矸石进入到破碎-填充孔隙-再破碎的循环过程中，试样孔隙率越来越低，4 MPa时定位点基本充满钢筒各处。4～10 MPa阶段内，应力水平较高，矸石试样被进一步压密，矸石之间的接触形式再次以摩擦为主，定位点数增加不明显，中下部核心区域越来越密集，说明试样进入到缓慢压密状态。整体来看，AE定位数随应力增加先增加后减少，与宏观变形的阶段变形规律协调统一[20]。

观察各组试样AE定位的三维分布图可以发现，破碎位置主要集中在钢筒的中下部，同时中部最为密集。分析原因，矸石在侧限压缩过程中，试样周围和底部受到钢筒的限制，上部矸石整体向下运动，中下部矸石受到挤压，上部试验力通过中部矸石向下传导，但是底部空间有限，固定的钢筒底座会产生反作用力，又通过中部矸石向上传导，上下合力共同作用下中部矸石的破碎程度最大。图7为不同应力阶段的 AE定位俯视图(v=1.0 kN/s)，观察俯视图可知，圆心和筒壁附近的定位点都较为稀疏，大多数定位点都集中于二者之间的菱形环状条带上，说明试样在向下压缩过程中，截面圆心附近的矸石具有侧向向外的运动趋势，同时钢筒侧限作用又使得筒壁附近的矸石具有侧向向内的运动趋势，所以筒壁到圆心的中间位置上受到双向挤压，破碎最为明显[21]。

图7 不同应力阶段的 AE定位俯视图(v=1.0 kN/s)Fig.7 Top view of AE location at different stress stages (v=1.0 kN/s)

图8为不同加载速率试验组最终的AE定位分布图，由图可知，v值越小的试样，内部破碎产生的AE事件越多，定位点分布范围越大，而且核心分布区域的密集程度越大。其中，v=2.0 kN/s时，定位点分布范围最小，AE定位数最少。

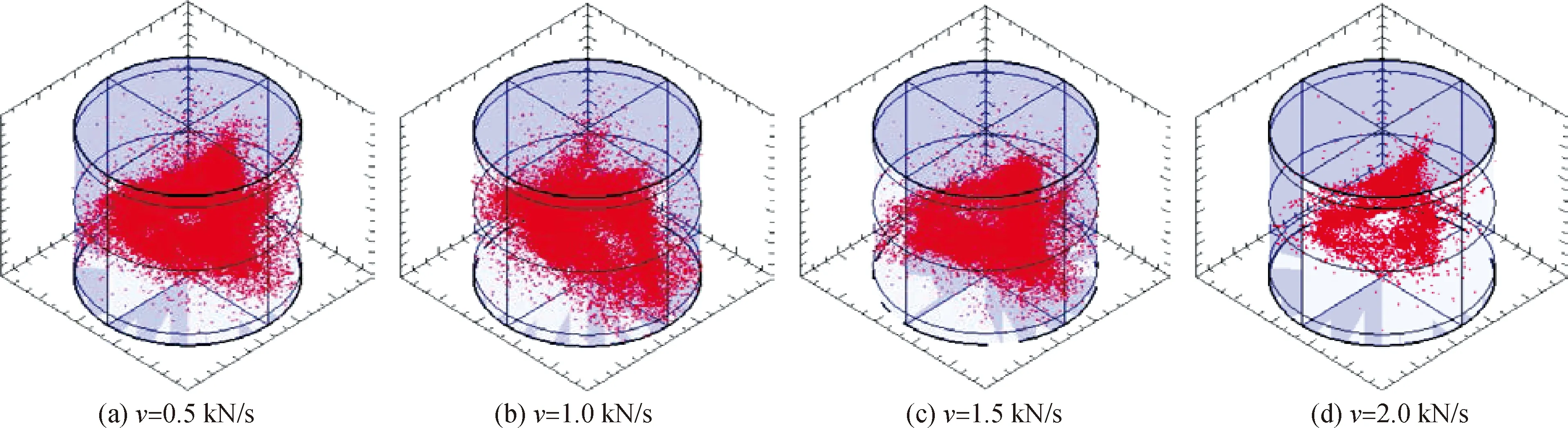
图8 加载速率影响下AE定位分布图Fig.8 AE location distributions under the influence of loading rate

4 结 论

(1)矸石的侧限压缩量是孔隙率变化量的宏观体现，低应力状态下对孔隙的直接压缩是影响宏观变形的主要因素。孔隙率随着矸石剩余高度的减小而减小，随着应变的减小而增大，与应力呈单调递减的反比例型复合函数关系，且递减速率逐渐减小。

(2)不同试验条件下矸石侧限压缩过程中的AE定位变化规律相似：AE定位数随着试验力的增大而不断增加，不同变形阶段定位点数相差较大；AE定位数随应力的增大先增加而后减少，与宏观变形的阶段性规律协调统一；破碎位置主要集中在钢筒的中下部，同时中部最为密集；AE定位数随加载速率的增大而减少。

(3)加载速率越大，对试样的压缩效果越明显，进而宏观变形越大；破碎程度随加载速率的增大而减小，但是对宏观变形的影响程度较弱。