一种高速多体船的纵向减摇预测控制方法

温 昊,张 军,胡浩俊,李国胜

(1.江苏大学 电气信息工程学院,江苏 镇江 212013；2.哈尔滨工程大学 智能科学与工程学院,黑龙江 哈尔滨 150001)

高速多体船具有宽大的甲板面积，装载量大，横向稳定性好，操控性强，适合作为高速渡船、军用高性能攻击艇和高性能隐身艇的基础船型[1].然而，在高速航行时多体船细长的侧体使得纵向倾覆力矩较大，恢复力矩较小，导致纵摇和升沉变化幅度过大，严重影响航行性能[2]，因此，必须对高速多体船进行减纵摇.目前，高速多体船主要安装T型翼和压浪板两类主动式减摇附体实现减摇，在船艏底部加装T型水翼以降低多体船垂向运动响应，在船艉加装压浪板以改善船舶运动姿态.然而，这2类减摇附体有着严格的输入约束[3]，减摇控制中减摇附体若长期处于饱和状态，则减摇控制性能下降，严重时会导致动态失速，造成高速多体船倾覆.

高速多体船的升沉和纵摇运动存在强耦合，且水动力学系数随航速变化而变化，系统呈现时变性，这给减摇控制带来困难.目前高速多体船减摇控制研究较少，文献[4]采用纵摇和升沉2个通道分离，设计比例微分减摇控制律，基于传递函数设计升沉和纵摇解耦矩阵，大幅限制了升沉和纵摇运动幅度，但是解耦矩阵鲁棒性较差，需要精确获得多体船水动力学系数.为了提高鲁棒性，文献[5-6]提出了多变量H∞鲁棒控制策略，但是该方法考虑最坏情况设计控制器，控制性能比较保守.更为严重的是，上述研究很少考虑减摇附体的输入约束问题，如果考虑控制约束，控制律需要重新设计.预测控制是解决输入约束的有效途径之一[1,7-9]，文献[1]采用预测控制对高速渡船进行减摇，采用滚动优化处理减摇附体的输入约束，避免附体长期处于饱和状态，并与H∞鲁棒控制进行减摇性能对比，结果表明预测控制的减摇性能明显高于H∞鲁棒控制，但是鲁棒性较弱.

针对上述问题，笔者采用前馈补偿+反馈的控制策略，提出有限时间扩张观测器+预测控制减摇方法.首先，建立由T型水翼和压浪板作为减摇附体的高速多体船控制模型，将控制模型分解为降维的时变模型和耦合量2项，减少多体船模型的复杂度.其次，设计有限时间扩张观测器，在线快速估计升沉和纵摇运动的耦合项，提高鲁棒性；针对降维的时变升沉和纵摇的通道提出单步预测控制策略，保证减摇附体满足约束.最后，将预测控制量和补偿量进行综合，通过仿真验证所提算法的有效性.

1 高速多体船的垂向运动模型

在高速多体船上安装T型水翼和压浪板，利用翼面产生的恢复力和力矩来抵消波浪的干扰力和力矩，从而减小升沉和纵摇的幅度.假设多体船以稳定航向和定常速度在无限深水域航行，水下部分的片体足够细长，波浪扰动引起的船体运动微幅，不考虑风和流对运动的影响.在海浪扰动作用下，其垂向的升沉和纵摇耦合运动的数学模型分别为

FT-foil+Fflap+Fwave，

(1)

MT-foil+Mflap+Mwave，

(2)

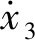
MT-foil=FT-foillT-foil，

Mflap=Fflaplflap,

式中：ρ为海水密度；A为T型翼面积；CL为水翼的升力系数；v为流体相对水翼的速度；CL1为压浪板升力系数；S为压浪板的有效面积；α1为压浪板攻角；α2为T型翼攻角；lflap和lT-foil分别为压浪板和T型翼的力臂.

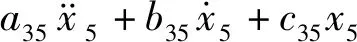
高速多体船的减摇控制目标是减少升沉和纵摇运动幅度，保证附体输入满足约束.预测控制是解决输入约束和多变量耦合控制的有效途径，但是高速多体船是四维耦合模型，在线优化计算量较大，难以直接应用于工程.为简化预测控制模型的复杂性，这里将多体船升沉和纵摇耦合运动模型分解为2个降维的单入单出模型，分别为降维的升沉和纵摇模型设计局部预测控制器.然后，采用有限时间扩张状态观测器，分别估计升沉和纵摇的耦合项以及干扰项，将估计值用于对降维系统的前馈补偿，从而降低升沉和纵摇运动的计算复杂度，提高系统稳定性和抗干扰能力.控制框架示意图见图1，其中U1和U2分别为纵摇和升沉通道的虚拟控制量.

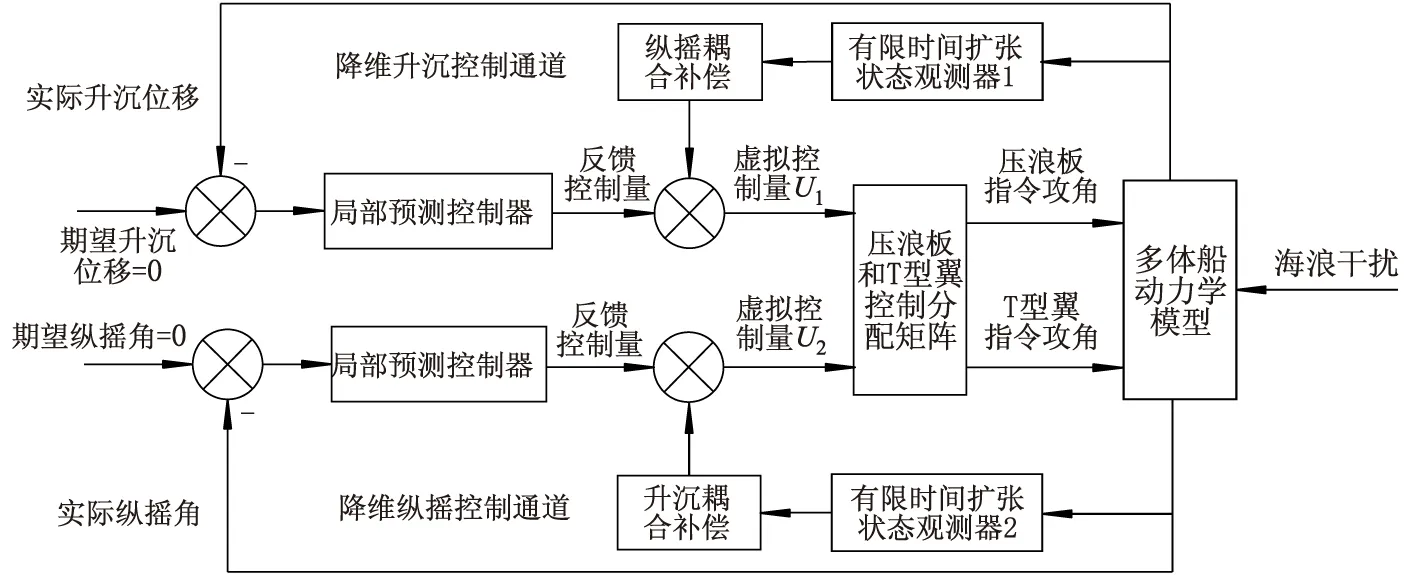
图1 高速多体船的纵向减摇控制框架示意图

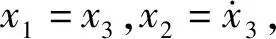
(3)

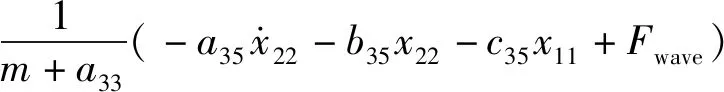
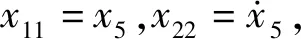
(4)

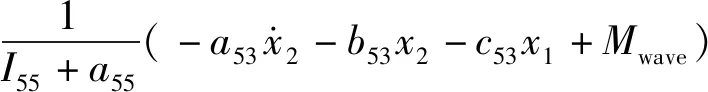
为了提高降维的升沉运动模型(3)的鲁棒性，需要在线实时观测纵摇通道耦合到升沉通道的运动量，以及升沉通道的外部随机扰动.由于有限时间观测器能够在给定的时间内实现状态的精确重构，以及快速估计干扰[10]，为此提出了有限时间扩张观测器.根据增益调度，多体船的水动力学参数表示为

(5)

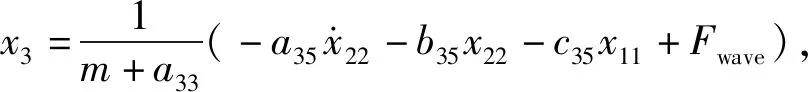
(6)

设计了一种非齐次的有限时间内收敛的扩张状态观测器，即

(7)

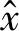
(8)

2 单步预测控制

上一节采用有限时间扩张观测器可以在线快速估计升沉和纵摇通道的耦合量，起到解耦补偿作用，但是高速多体船系统的减摇效果还需要反馈控制律来保证.文献[4]采用经典PD控制以实现纵摇和升沉的镇定，并未考虑最优的减摇控制性能.预测控制突破了传统鲁棒控制思想的限制，综合利用多变量被控对象的历史信息和模型信息，对目标函数不断进行滚动优化，并根据实际测得的对象输出修正或补偿预测模型，使控制性能和鲁棒性得以提高[11].与此同时，预测控制能很好地处理输入约束，适用于时变系统.本节采用预测控制设计反馈控制量，则降维的升沉通道系统模型可写为

(9)

由于预测控制为离散算法，因此对式(9)进行离散化：

xk+1=A(k)xk+B(k)uk，

(10)

其中xk=[x1(k),x2(k)]T.预测模型(10)为二维模型，没有纵摇耦合量，复杂性显著降低.基于无限时域预测的线性矩阵不等式优化能很好地解决输入约束，但是保守性较大[12]，笔者提出单步预测控制，其优化目标函数为

(11)

式中：Q、R为加权矩阵；P为终端代价项.为简化书写，将A(k)和B(k)分别记为A和B，给出下面的设计结果.

引理1[13]如果A、C为非奇异的，则下面的等式成立:

(A+BCD)-1=A-1-A-1B(C-1+DA-1B)-1DA-1，

(12)

(I+AB)-1A=A(I+BA)-1.

(13)

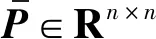
(14)

证明在离散时变线性系统(10)中，使得目标函数(11)最小的最优控制满足如下条件：

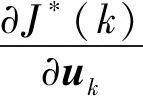
(15)

式中：P为终端代价项的加权矩阵.因此有

(16)

令k+1时刻可行的近似最优控制律为K，当前时变模型[A(k),B(k)]单步预测的动力学模型为

xk+2=(A+BK)xk+1，则相邻时刻的优化目标函数之差为

J*(k+1)-J*(k)≤J(k+1)-J*(k)=

P+KTRK](A+BK*)-(Q+K*TRK*)}xk.

(17)

根据引理1的公式(12)，有

A+BK*=(I+BR-1BTP)-1A.

(18)

同时，最优控制增益K*可写为

K*=-R-1(I+BTPBR-1)-1BTPA.

(19)

根据引理1的公式(13)得到

K*=-R-1BTP(A+BK*).

(20)

进一步有

(A+BK*)T[(A+BK)TP(A+BK)+Q-P-

PBR-1BTP+KTRK](A+BK*)-Q<0.

(21)

为了保证预测控制的滚动优化渐近稳定，要求J*(k+1)-J*(k)<0，则需要下面条件成立:

(A+BK)TP(A+BK)-PBR-1BTP+

KTRK+Q-P<0.

(22)

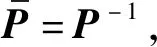
下面考虑输入约束，控制升沉的最大反馈控制量为

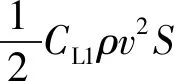
(23)

考虑有限时间观测器干扰估计的前馈补偿后，则单步预测控制的最大反馈控制量为

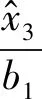
(24)

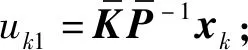
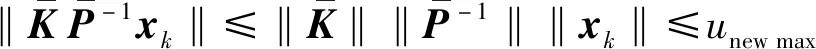
(25)

则新的矩阵计算公式为

(26)

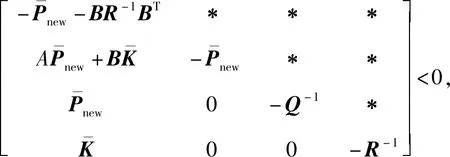
(27)

(28)

(29)

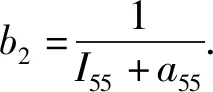
(30)

3 仿真分析

采用文献[3]的多体船模型，验证预测控制减摇的有效性.多体船航速为40 km·h-1，迎浪航行，海浪遭遇频率取值3.25 rad·s-1.多体船在高速航行时受到的海况等级为4级海况，海浪采用P-M谱进行仿真.4级海况P-M谱函数的表达式为

(31)

式中：vζ为海面以上高度为19.5 m处的平均风速；g为重力加速度.根据切片法，通过数据拟合和叠加的方法，求得不同海浪遭遇频率值时海浪作用于多体船的干扰力和干扰力矩.海浪干扰力、干扰力矩与时间关系曲线分别如图2-3所示.

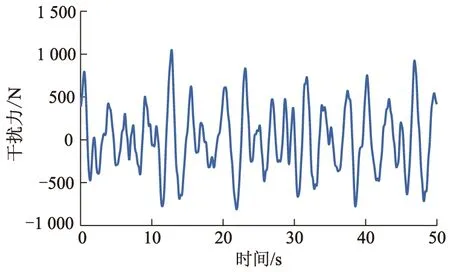
图2 海浪干扰力与时间关系曲线

考虑T型翼以水平方向为基准在[-15°,15°]的范围内转动，压浪板以水平方向为基准在[0°,15°]的范围内转动，分别对采用预测控制器与不采用控制器的多体船垂向运动进行仿真，仿真结果如图4-5所示.

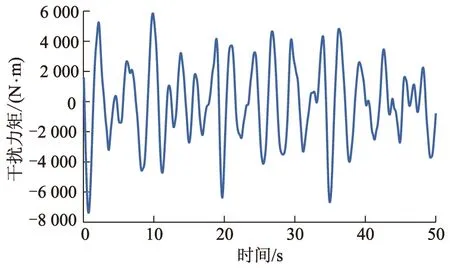
图3 海浪干扰力矩与时间关系曲线

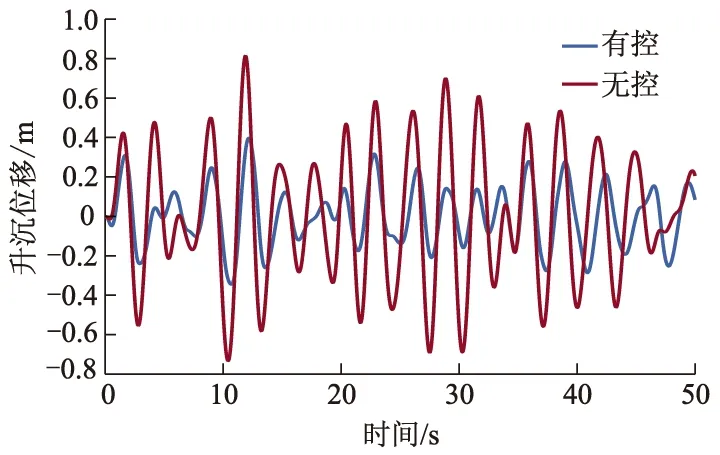
图4 多体船升沉位移与时间关系曲线

基于2种控制律的升沉位移、纵摇角与时间关系曲线分别如图6-7所示.有控时T型翼和压浪板的攻角与时间关系曲线分别如图8-9所示.

从图4和图5可以看出，与无控情况相比，采用预测控制的升沉位移减少40%～50%，纵摇角减少50%～65%，这说明对于双通道的耦合处理策略合理有效.图6和图7仿真结果表明，笔者提出的预测控制减摇性能明显比文献[8]减摇效果好，这是因为有限时间观测器的前馈补偿有效地提高了系统的鲁棒性.图8和图9仿真结果表明，预测控制减摇保证了T型水翼和压浪板输入满足约束.

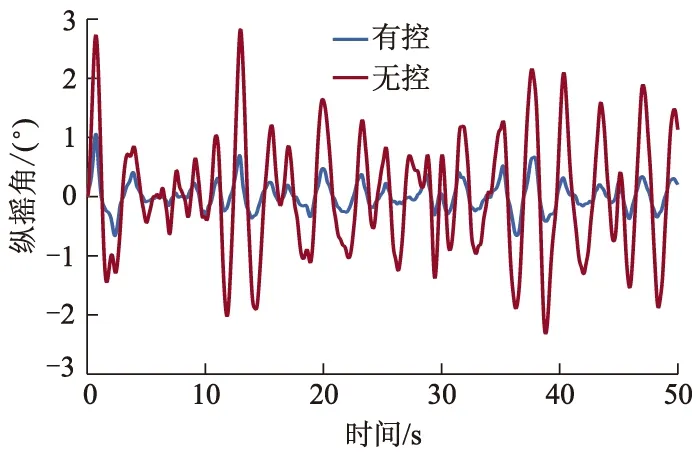
图5 多体船纵摇角与时间关系曲线

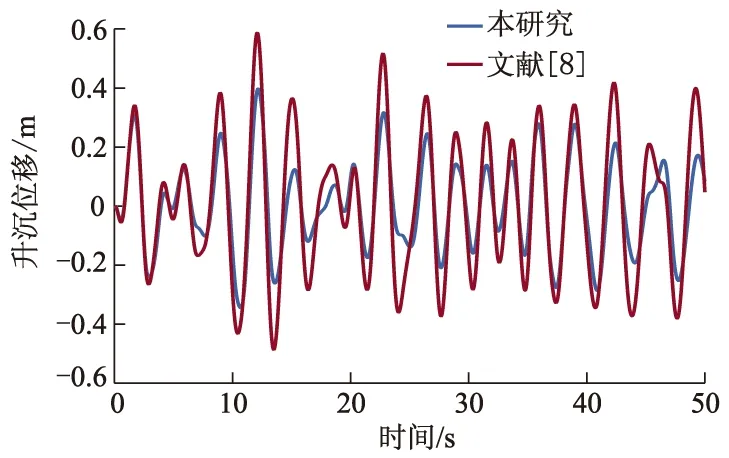
图6 基于2种控制律的升沉位移与时间关系曲线

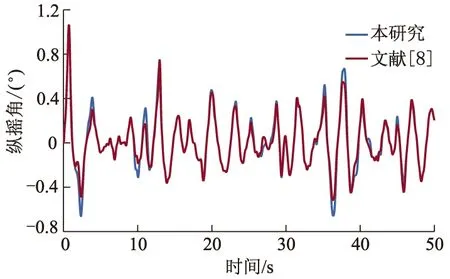
图7 基于2种控制律的纵摇角与时间关系曲线

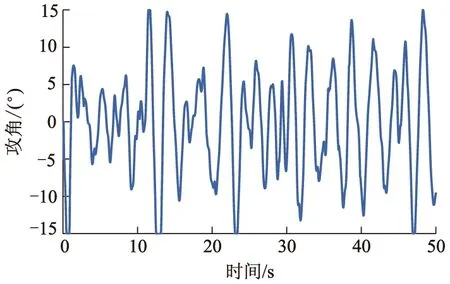
图8 有控时T型翼的攻角与时间关系曲线

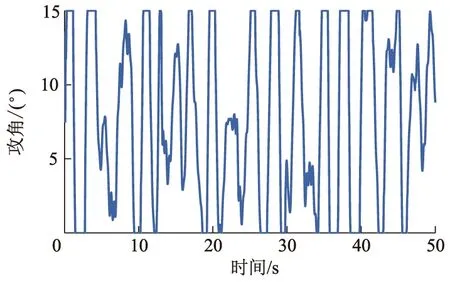
图9 有控时压浪板的攻角与时间关系曲线

4 结 论

1)建立由T型水翼和压浪板作为减摇附体的纵摇和升沉的控制模型，并将控制模型分解为降维的单入单出模型和耦合量2项.

2)设计了有限时间扩张观测器，进行在线快速估计纵摇和升沉运动的时变耦合项，进行实时前馈补偿.

3)提出了局部单步预测控制，提高了系统的减摇性能，保证减摇附体满足约束.