基于改进β样条理论的自主泊车路径规划
吴飞龙,郭世永
(青岛理工大学 机械与汽车工程学院,山东 青岛 266520)
随着汽车保有量的增加,城市道路交通压力日益增加,驾驶员行车与停车的环境也变得越来越复杂[1],泊车作为驾驶行为的重要组成部分,已经成为安全事故高发的驾驶环节.自主泊车技术可以减小驾驶员在面对狭小空间泊车时的难度,同时也提高了驾驶员舒适性和泊车安全性[2].自主泊车又称为代客泊车或一键泊车,既可以做到让驾驶员可以在指定地点处召唤停车位上的车辆,又能让当前驾驶的车辆停入指定或随机的停车位.其关键技术主要包括车位识别、路径规划、路径跟踪控制(执行控制)[3-4].
自主泊车的路径规划包括全局路径规划和局部空间路径规划[5].国内外学者已对此进行了大量的研究,文献[6]基于改进后的五阶多项式泊车路径,通过针对性地设计罚函数,采用遗传算法计算得到最佳泊车路径和最小泊车空间.文献[7]提出一种经回旋曲线优化的泊车路径,解决了两段式路径规划在切点处曲率不连续问题,并给出相应的路径计算方法.文献[8]通过建立前进和后退的模糊规则,来控制汽车的转向角,从而实现平行泊车的轨迹规划.文献[9]考虑车位的几何约束,采用基于最小转弯半径的圆弧曲线与直线连接的方式,来求得不同工况下的泊车路径.文献[10]基于模糊控制理论,设计了三段式的平行泊车控制算法.文献[11]以最短路径为目标,采用遗传算法对垂直泊车路径进行优化,可扩大泊车初始区域.文献[12]综合考虑平行泊车碰撞情况,以泊车终点处车辆航向角最小化为目标,建立了含避障约束、车辆转向盘转角及角速度约束等多个非线性约束的泊车路径函数,基于β样条理论获得曲率连续、变化缓慢的泊车路径.
笔者提出一种基于改进β样条理论法的自主泊车路径规划方法,建立泊车运动学模型、自身物理条件约束、路径避障约束、车辆转向盘转角及角速度约束,根据实际泊车场景,对3种工况下的平行泊车模式进行仿真分析,验证提出的路径规划算法的可行性.
1 车辆运动学模型
由于泊车过程中车速较低,轮胎侧滑可以忽略不计,因此采用纯滚动车辆运动学模型[5].如图1所示,其中:l为轴距;W为车身宽度;f、r分别为前悬、后悬长度;P为车辆后轴中心;O′为瞬时转向中心;θ为车辆航向角;φ为前轮等效摆角.
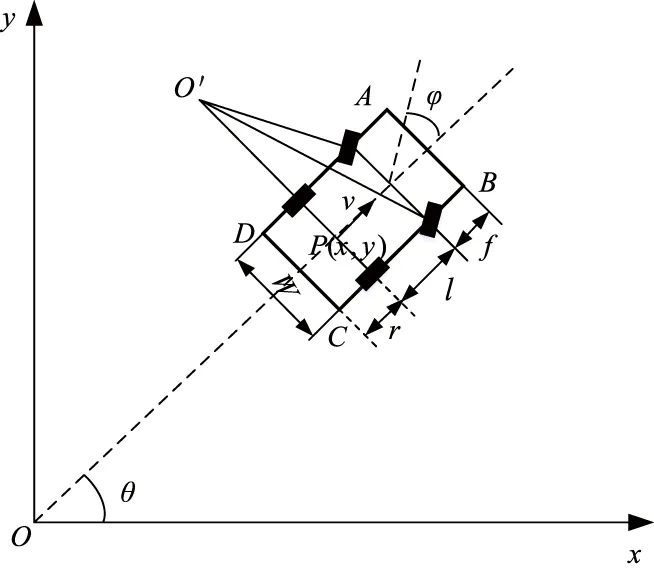
图1 车辆运动学模型
根据运动学模型,可以得到泊车的运动学微分方程:
(1)
式中:v为车速;a为加速度;ω为前轮摆角角速度.
车辆在泊车过程中,除了要考虑车辆运动学方程约束,还要考虑自身物理条件约束,其对状态量和控制量的约束如下:
(2)
式中:vm、am分别为泊车时的最大车速和最大加速度;φm、ωm分别为最大前轮摆角及其对应角速度.
2 平行泊车路径规划
泊车把握一个原则:不管是分几步泊车,首先要保证车辆在末位置不仅要满足车位底边的碰撞约束,还要使航向角尽可能小(有利于后续的泊车步骤).先设定末位置迭代航向角,泊车轨迹如图2所示,dx、dy为相应的安全阈值.首先设置航向角为0°,是否可以规划一条无碰撞路径,如果没有,缓慢增大航向角,直到找到一条满足碰撞约束的路径.
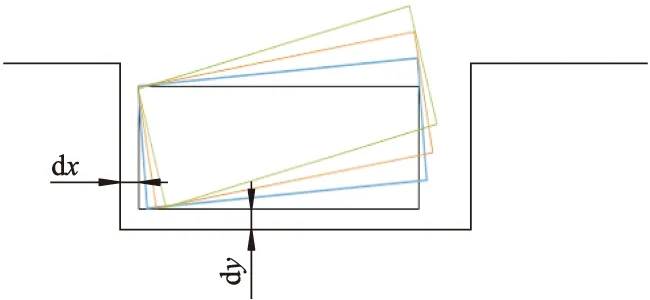
图2 泊车轨迹
2.1 碰撞点的预判
通常情况下,在车辆刚要驶入车位前(见图3a),存在2个碰撞点:一是车头外侧A点与周围物体的碰撞;二是车辆内侧CD边与车位顶点O的碰撞.在车辆刚好驶入车位到车辆完全完成泊车的过程中(见图3b),存在3个碰撞点,分别是车头内侧的D点、车尾两侧的碰撞B点和C点.
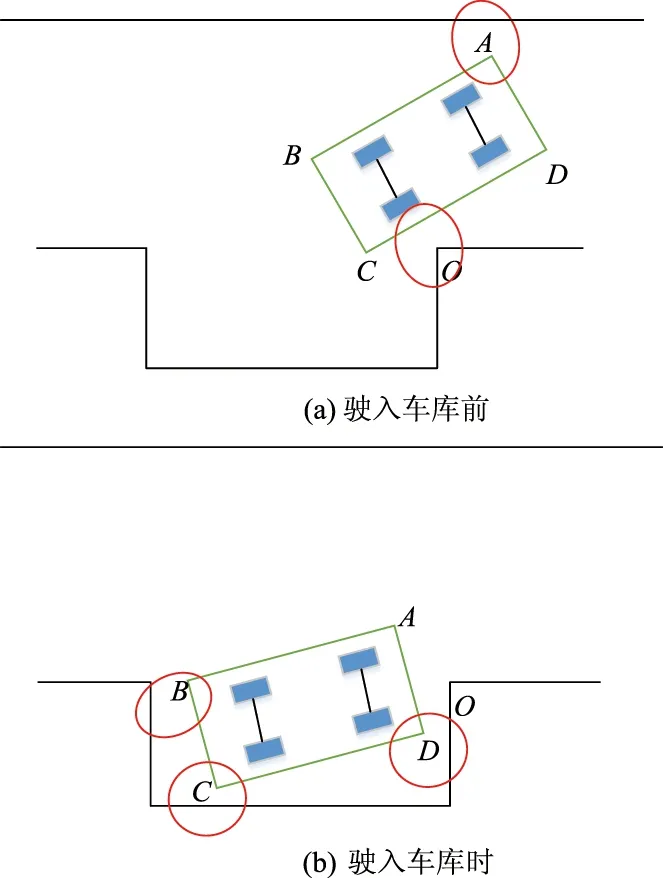
图3 泊车碰撞示意图
2.2 三段式路径规划算法设计
为使车辆行驶路径的曲率及曲率变化率较小,采用三段式的泊车路径,即圆弧+切直线+圆弧模式.泊车动态图如图4所示.
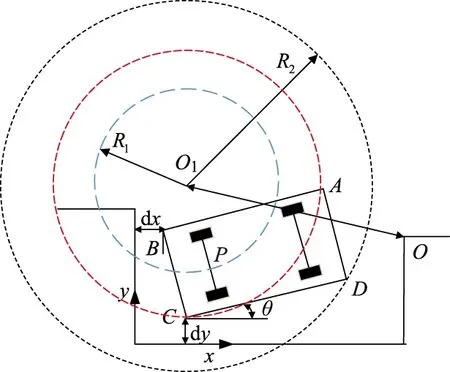
图4 泊车动态图
红圆为车辆顶点C走过的圆弧,设定车辆的末位姿,即车辆完全驶入车位且回正后,车辆BC边、CD边与车位的安全距离分别为dx和dy,满足车辆B、C点的碰撞约束.由图4可以确定B、C点的坐标分别为(XB,YB)、(XC,YC).假设车长为L,可求得车辆航向角,后轴中点P的坐标(XP,YP),即
(3)
由P点坐标可得圆心O1的坐标(XO1,YO1),其坐标值为
(4)
式中:rmin为车辆最小转弯半径.
由后轴中心点坐标可求得车辆D点坐标(XD,YD),即
(5)
由此可求得车辆D点轨迹圆的半径R2以及圆心O1到车位右顶点O的距离LO1O.若LO1O-R2≥d,d为安全阈值,则满足车辆点D与车位右边的碰撞约束,否则不满足,需进行下一步计算.
计算圆心O1到车位右边距离为LO1O+d的点,如图5所示,假设E点恰好为此临界点.O点坐标 (XO,YO)已知,分别求线段O1E与y轴平行半径的夹角θ1和线段O1D到与y轴平行半径的夹角θ2,即

图5 泊车空间约束示意图
(6)
由此可得角θerror=θ1-θ2.此差值映射到以后轴中心P为轨迹的圆(蓝色的圆)上,也就是说P点的轨迹圆的可行驶范围是圆心角为[θP,θP+θerror].求得P点轨迹圆在角θP+θerror的x轴坐标值X*作为判断是否满足碰撞约束的阈值,即
X*=XO1+R1cos(3π/2+θP+θerror).
(7)
泊车初始位置如图6所示,车辆与库右边的安全阈值dh确定(y坐标确定),沿后轴中心线向右迭代泊车起始点不同的x坐标,计算第1段圆弧和切线方程.判断是否满足第2碰撞约束.
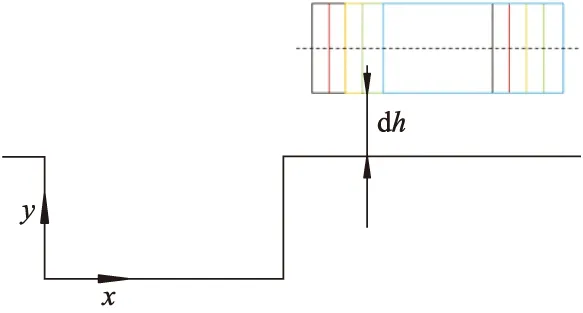
图6 泊车初始位置
泊车轨迹规划如图7所示,车辆泊车起始位置后轴中心P1坐标 (XP1,YP1),由圆心O1坐标和圆心O1′坐标(XO1′,YO1′)得与切线相交中点L的坐标(XL,YL),可进一步得到线段LO1的长度LLO1,θa、θb、θe以及切点K的坐标 (XK,YK)如下:
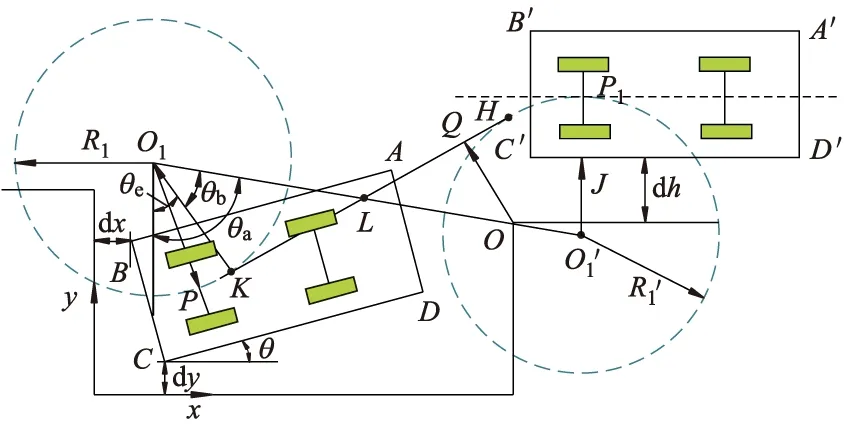
图7 泊车轨迹规划图
(8)
式中:R1为后轴中心P的轨迹圆半径.
圆O1与圆O1′半径相等,即R1=R1′,同理可得切点H的坐标 (XH,YH),即
(9)
最终可得切线HK的方程.
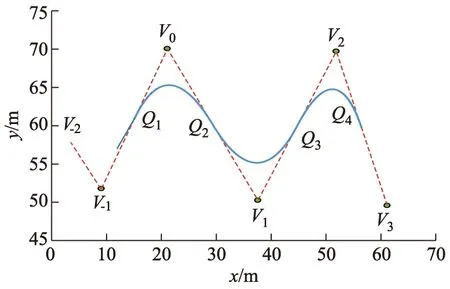
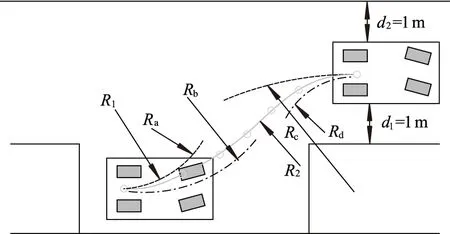
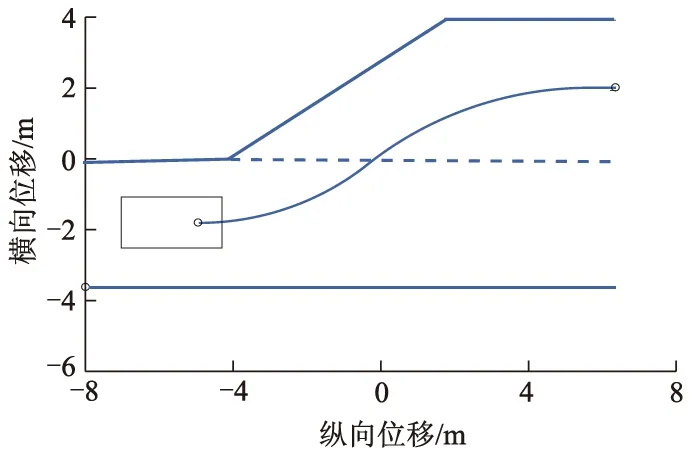
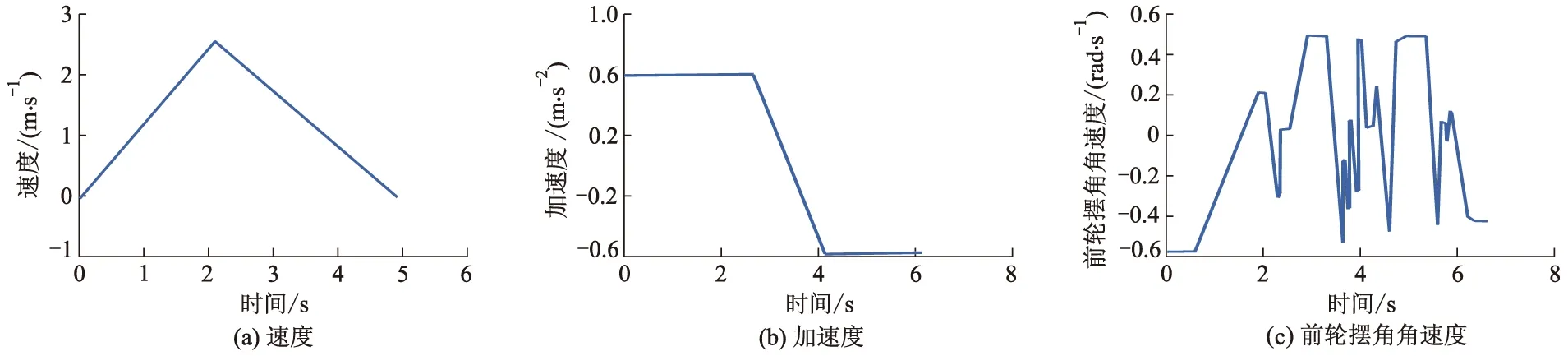
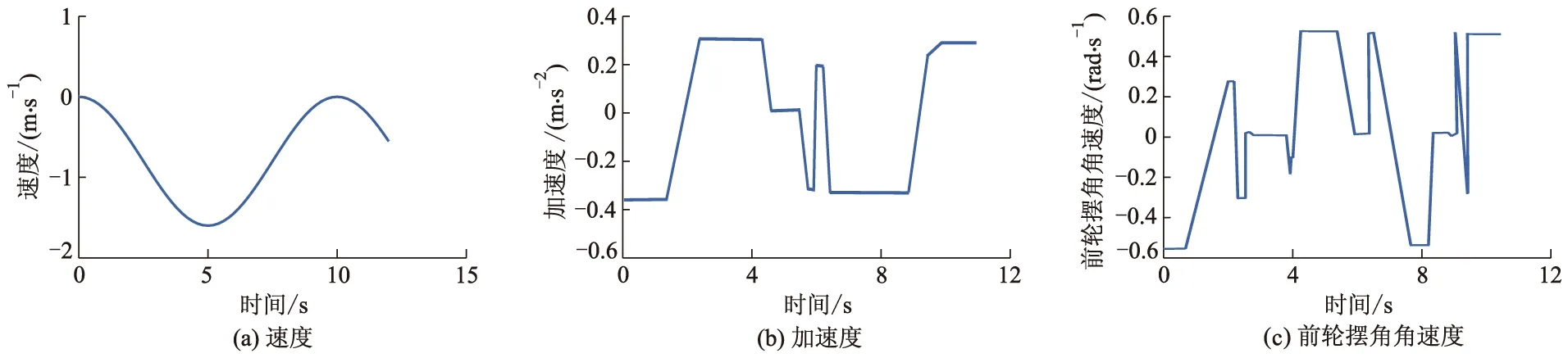
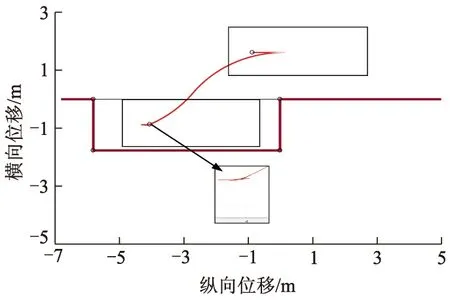
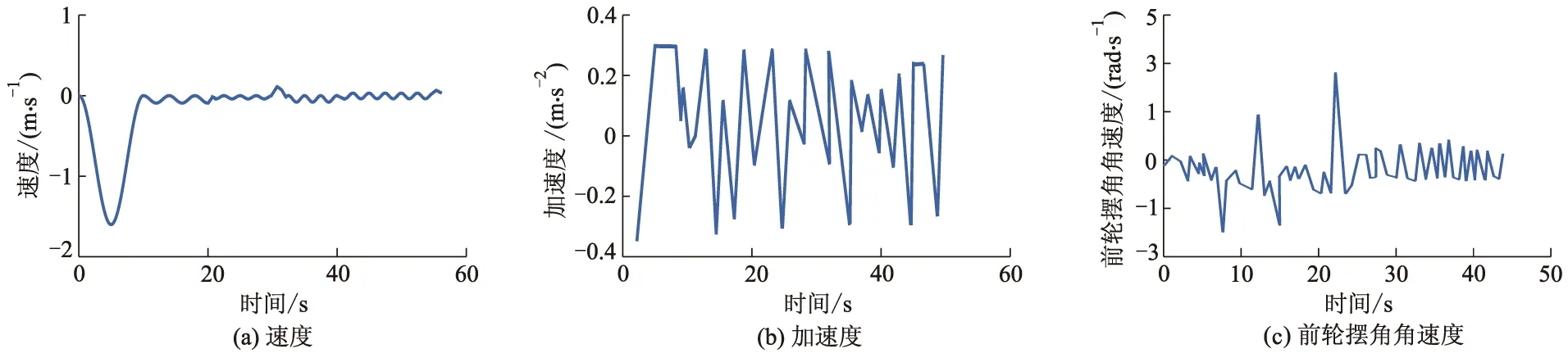
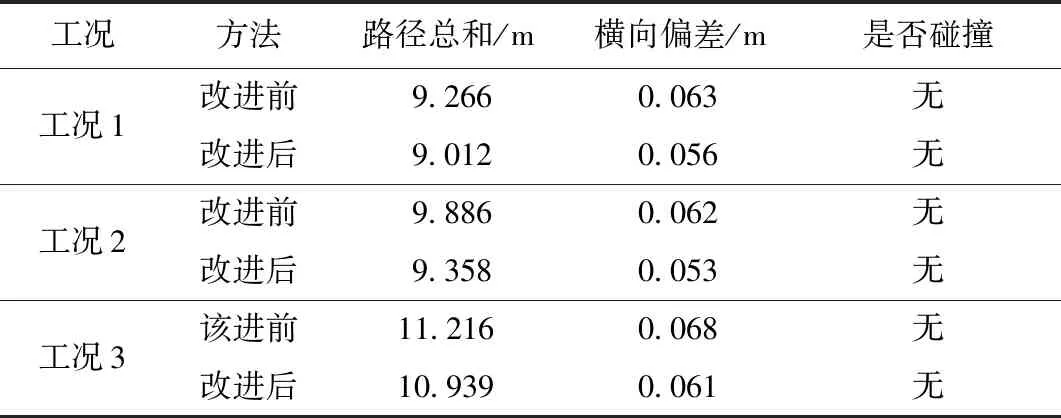
从图7可以看出,车辆CD边与库顶点O的碰撞可能在圆弧阶段或者切线阶段,因此,应当判断其临界点.经分析,当过O点作垂直于切线的直线,当与切线的交点恰为切线与圆的切点时,为临界点.易求得交点Q的坐标为(XQ,YQ),后轴的延长线与车身一侧的交点为J.当XH≥XQ时,碰撞约束的判断条件为LOQ≥0.5W+d;当XH 程序流程图如图8所示. 图8 泊车程序流程 三段式路径规划算法既能根据车库大小和车辆尺寸,通过迭代自适应找到泊车起始区域和最佳起始泊车点,同时又保证第1次入库车辆航向角相对最小,并且能形成一条完整的无碰撞泊车路径,以便后续泊车动作,但路径曲率的连续性不够好,且曲率变化率相对较快,难以控制,曲率的变化不足以满足车辆运动学以及EPS(electric power stee-ring)的性能要求. 路径优化需满足以下3个目标:① 优化之后依然是无碰撞路径;② 优化后的路径曲率沿样条必须有界;③ 其曲率的变化必须满足车辆运动学以及EPS的性能要求.β样条曲线是阶导数连续的分段曲线(如一阶和二阶),即使在相邻段的节点处也是如此,这种曲线由一组控制顶点所确定,这些顶点按顺序连接就构成了一个控制多边形.曲线趋向于模拟控制多边形的整体形状. 现让控制多边形由控制点序列 [v-2,v-1,v0,v1,…,vm]所组成,每个点由它的笛卡尔坐标所确定.曲线将由m-2段组成,第i段曲线记为Qi(u),如图9所示,它由4个控制顶点 (Vi+r,r=-2,-1,0,1)所确定,这段曲线上的任何点都是这些控制点的加权平均值,第i段曲线上点的坐标为 图9 样条线和控制点 (10) 式中:br为权重系数,是评估在任何参数u范围内以及每个形状参数β1、β2下的标量函数,形状参数决定了曲线模拟控制多边形的方式. 有研究[13]表明,当需要平滑的曲率变化时,三次样条曲线是最佳选择.在这种情况下,β1=0,β2=0,权重系数定义为 (11) β样条曲线最重要的特性之一是保凸性,这一特性保证了曲线经过的表面以控制多边形为界,如图10所示. 图10 圆弧上的控制点 如果控制点在一段圆弧上面,可以推导出结论:控制点之间的距离是有规律的,一段β样条曲线段的控制点在半径为R的圆弧C上,如图10所示,如果控制点之间的距离为δ,那么δ≤πR/6,β样条曲线段在圆C′的外面,那么圆C′的半径为 (12) 进一步通过试验表明:曲线段的曲率半径上界为R,下界为R′[13].因此,如果曲线段的曲率半径的值要保持在R与R′之间,那么,δ应该满足: (13) 这个约束也保证了曲线段在圆弧之间. 优化后的轨迹如图11所示,Ra、Rb分别为R1的最大值和最小值;Rc、Rd分别为R2的最大值和最小值. 图11 轨迹优化图 在R1段圆弧上取控制点,由β样条曲线的保凸性,原路径无碰撞,那优化之后的路径也无碰撞.在R2段圆弧取控制点,Rd为避免碰撞的最小转弯半径,因此可得 (14) δ≤min(δ1,δ2,δ3), (15) 式中:δ1为第1个控制点与第2个控制点间的距离;δ2为第2个控制点与第3个控制点间的距离;δ3为第3个控制点与第4个控制点间的距离,后面以此类推. 为保证生成的样条可被执行,第1段及第2段圆弧生成的样条曲线的曲率半径要大于车辆自身的最小转弯半径Rmin,即 (16) 尽管β样条曲线生成的路径是曲率连续的,但 曲率的变化应该足够满足有效路径跟踪的平顺性的要求,通过试验表明:按β样条曲线进行平行泊车的控制策略,如图12所示,其曲率的变化满足以下线性关系: 图12 样条曲线曲率 (17) 式中:ρ为曲率;ρ1为S0至S1间的曲率;ρ2为S4至S5间的曲率;s为弧长;k1、k2、k3为曲率系数. 如果v表示汽车行驶的线速度,其按照样条曲线行驶的曲率改变的速度满足: (18) 式中:[t0,t1]、[t2,t3]、[t4,t5]为曲率改变的时间段. 曲率变化的速率为 (19) (20) 根据式(18)和式(20),转向机构要正确遵循曲率的变化,δ需满足以下约束: (21) 式中:k1、k2、k3分别取6.6、3.2、6.6. δ的选择及转角变化如图13所示.图13a表明该控制策略没有遵循式(21),因而导致路径跟踪的精度不高.由于汽车不能遵循转向角的变化(见图13b),由图13c可见,通过保持δ的值,并减小速度v的值(δ5,δ6,δ7的值减小),路径跟踪的精度很高.由图13e可以看出:通过保持速度v的值而增加δ的值直到它满足式(21)的要求,其表现出来的控制效果也较好. 图13 δ的选择及转角变化 当β样条曲线生成后,δ的值应该被使用,根据式(14)-(16)和式(21),δ的值必须满足: max(δ5,δ6,δ7)=δvel≤δ≤δcol=min(δ1,δ2,δ3,δ4), (22) 式中:δvel、δcol分别为控制点间距的上界和下界. δvel被选择后,要保证δvel选择满足约束δf≤δcol,δf为满足约束条件后的控制点间距. 考虑到(δ1,δ2,δ3,δ4)主要与几何约束有关,根据式(21),(δ5,δ6,δ7)主要取决于车辆的速度和转向系统的速度,这可能会造成δvel>δcol,换言之,它可能会得到一种连续曲率的控制策略,但是该策略不是无碰撞的.在这种情况下,为了获得一个无碰撞的策略,δ应选为δ=δcol.然而,根据式(21),如果该准则被应用,由于在这个速度下,车辆转向系统不能很好地执行曲率的变化,原始速度的值一定会被改变.因此在这种情况下,为了使车辆尽可能正确地沿着样条曲线路径行驶,速度v的值应该减小.因此,由式(21)可知,速度v的上界为 (23) 然后vmax=min(v1,v2,v3)被选为新的v值. 由Matlab/Simulink搭建仿真平台,建立平行泊车多种场景验证基于改进β样条理论法规划自主泊车路径的有效性,采用某大众车为研究对象,车辆参数及约束参数如下:l为2.578 m;f为0.918 m;r为1.076 m;W为1.769 m;vm、am分别为3 m·s-1、0.72 m·s-2;φm、ωm分别为0.56 rad、0.56 rad·s-1.规定车辆沿车道线水平向右为速度正方向. 1)平行泊车工况1,此工况下设定车道宽度为3.5 m,车位宽度为4.0 m,选(-1.70,-5.00)m作为后轴中心起始位置,此时,车身与两侧车道线保持平行,汽车终止的条件为完成泊车后,后轴中心点在车位中心线上,且车身与车位保持平行,如图14所示,车辆满足上述泊车要求,在泊车过程中并未发生碰撞.泊车工况1状态量与控制量如图15所示,状态量和控制量均满足约束条件. 图14 泊车工况1路径示意图 图15 泊车工况1状态量与控制量 2)平行泊车工况2是停车场内常见的平行泊车位,该工况下设定车位的宽度为1.9 m,车位的长度位7.0 m,该工况下选(0.16,-1.00)m作为汽车后轴中心的起始位置,汽车初始位置时,车身与车位保持平行,汽车完成泊车的条件如下:汽车完成泊车时,汽车后轴中心点在车位中心线上,且车身与车位保持平行,如图16所示.汽车很好地一次性连续地完成泊车动作,且形成一条无碰撞的连续曲率路径.泊车工况2状态量与控制量如图17所示,该工况下,车辆的状态量和控制量均满足约束条件. 图16 泊车工况2路径示意图 图17 泊车工况2状态量与控制量 3)平行泊车工况3,该工况与工况2类似,均属于常见的平行泊车位,该工况与工况2的区别在于汽车的起始位置不同,车位的长度不同,此工况下设定(-0.86,1.60)m为泊车后轴中心的起始位置,汽车在初始位置时,车身与车位保持平行,汽车的终止条件与工况2完全一致,如图18所示,由于汽车初始位置离车位很近,车位相对狭窄,汽车不能一次性完成泊车动作,车辆在初始位置以及进入车位内都需经过多次前进和后退的调整,最终才完成整个泊车过程,但这一过程中均未发生任何碰撞现象.泊车工况3速度、加速度、前轮摆角角速度曲线如图19所示,该工况下部分控制量未满足约束条件,前轮摆角角速度超过最大值约束限制,这是由于车辆在车位内部调整时,车位相对狭窄导致车辆短暂的在原地转向. 图18 泊车工况3路径示意图 图19 泊车工况3速度、加速度、前轮摆角角速度曲线 改进前后2种工况下车辆横向位移对比如图20所示. 图20 改进前后车辆横向位移对比 由图20a可以看出:工况2下,在车辆快要进入车位的过程中,优化后的泊车轨迹横向位移比优化前小,且泊车轨迹更平滑.由图20b可以看出:工况3下,在车辆进入车位后的过程中,优化后的泊车轨迹横向位移的变化要略小于优化前.结合图20和表1可知,3种工况下,整个泊车过程中,优化后的路径总长要小于优化前,且泊车结束后后轴中心点与车位中心线的横向偏差优化后都要明显小于优化前. 表1 改进前后泊车性能对比 1)提出的泊车路径规划算法能指导车辆完成自主泊车,并最终到达指定的泊车位,且在自主泊车的过程中无碰撞发生. 2)提出的基于改进β样条理论法规划的路径曲率连续,曲率变化平缓,满足车辆运动学以及EPS的性能要求,并且泊车效率高. 3)提出的算法泊车路径总和减小了3%左右,泊车结束后后轴中心点与车位中心线的横向偏差也大大减小. 4)能实现狭窄泊车位内的自主泊车路径规划,但与真实的复杂泊车场景还有一定的差距,后续还需要考虑真实场景下的动态避障的规划.
3 基于改进β样条曲线的路径优化

3.1 控制点的选择

3.2 转速的约束
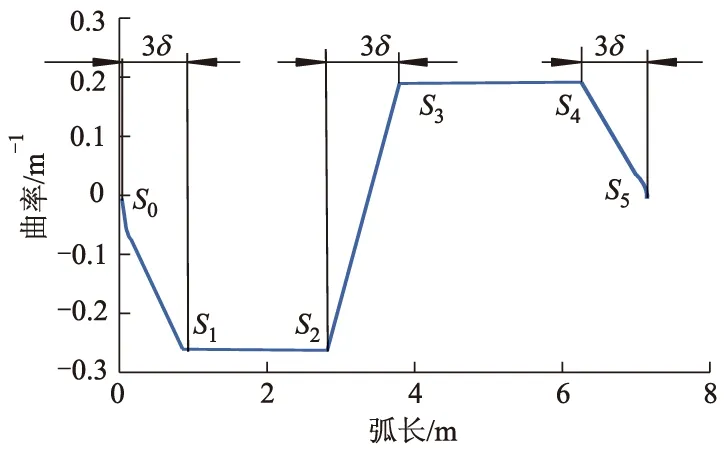
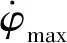
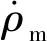
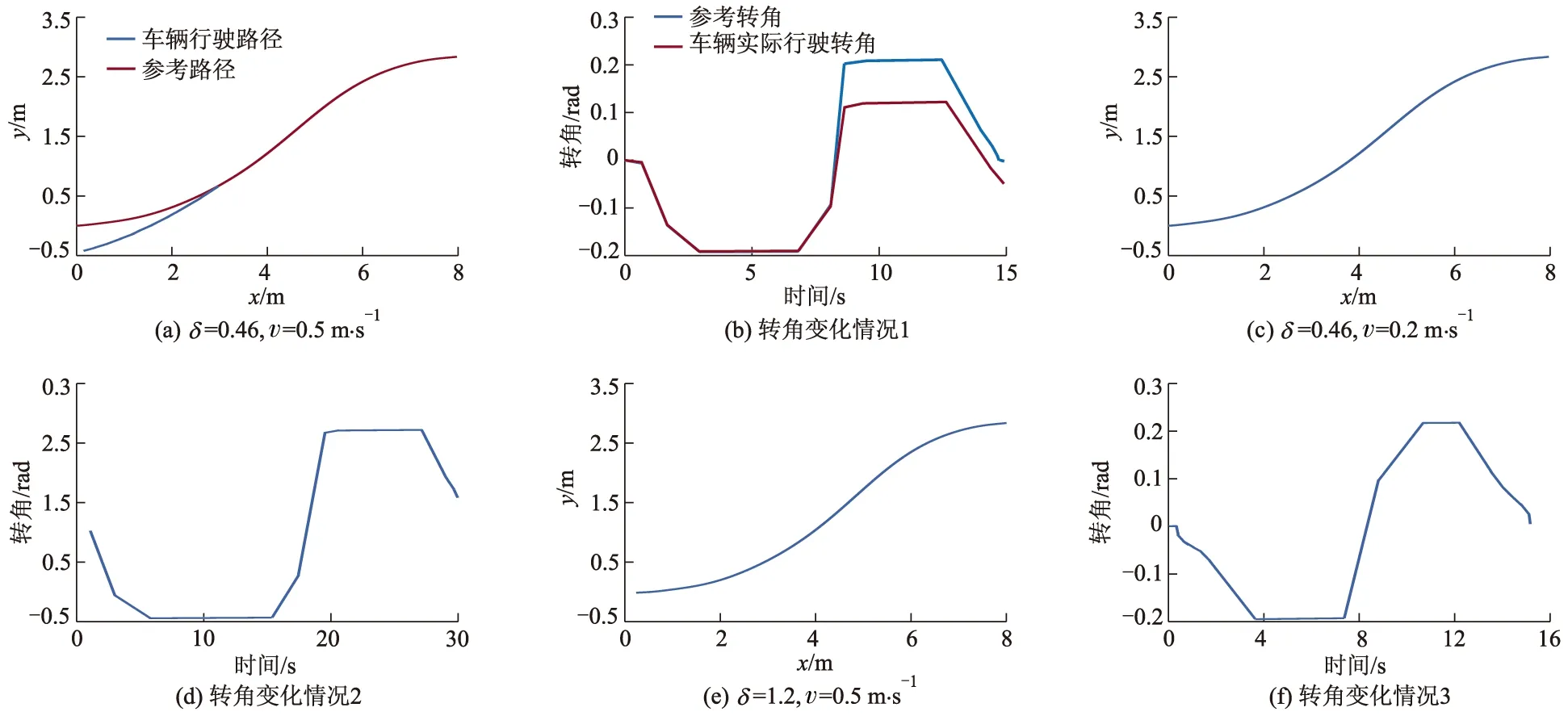
3.3 δ的选择
4 仿真分析


5 结 论

