纯电动汽车双电动机耦合驱动系统效率最优控制策略
李胜琴,丁雪梅,于 博
(东北林业大学 交通学院,黑龙江 哈尔滨 150040)
电动车辆具有低排放、能源利用多元化、高效化和易实现智能化等特点,各国政府都制定了积极的战略发展规划推动电动车辆的技术研发和规模化应用.但是提高续驶里程仍然是困扰纯电动汽车发展的关键性的难题.续驶里程除了依赖于蓄电池技术(提高电池功率密度和能量密度)外,还与动力传动系统的构型、参数匹配以及控制方法密切相关.因此,高效率的传动系统控制方法是提高纯电动汽车续驶里程及综合性能的重要研究方向.
国内外许多研究机构都在开展纯电动汽车驱动系统的开发研究,并均已取得一定的研究成果.武小花等[1]以提升纯电动客车经济性能为目标,提出了双电动机耦合驱动系统新构型,对2个电动机采用直接转矩控制,实现多个工作模式之间的切换.韩光伟[2]提出了基于行星齿轮机构的双电动机耦合驱动系统,针对爬坡、启动、高速、巡航等行驶工况提出转速和转矩的协调控制方法,结果表明双电动机耦合驱动系统效率大于80.0%工作区域面积占总工作区域面积的50.0%以上.鲁振飞[3]、ZHU B.等[4]提出双电动机耦合驱动系统新构型,并基于电动机需求功率最小的原则制定了模式切分控制策略,结果表明新型双电动机构型纯电动汽车的节能潜力达到10%左右.解少博等[5]、王勇[6]均对双电动机驱动电动汽车的动力分配控制策略进行了研究,提出了电动机转矩分配策略,可以改善电动汽车的节能潜力.J.KOWAL等[7]、LIANG J.等[8]以提升整车经济性能为目标,分别提出了效率最优控制策略及电动机工作模式切换策略,结果表明控制策略节能效果较好.M.D.CARLO等[9]提出了2个电动机通过行星齿轮传动组合的驱动方案.通过对动力系统参数优化分析,该系统在驱动时的平均效率相对于单电动机驱动时的平均效率提升8%.在制动能量回收过程中,一个循环工况内可以多回收1.86%的能量.
综合国内外相关研究现状可知,由于节能效果较好,双电动机耦合驱动是目前纯电动汽车比较常用的动力驱动系统方案.但是针对实际运行工况下驱动系统效率的双电动机的工作模式切换方式及动力分配控制策略研究,还相对较少.
笔者在某单电动机驱动电动汽车的基础上,提出双电动机耦合驱动系统构型,以整车驱动系统效率最优为控制目标,制定多模式切换及动力分配的驱动系统控制策略,在保证原车动力性的基础上,提高此纯电动汽车的节能潜力.
1 双电动机耦合驱动系统构型分析
1.1 双电动机驱动系统构型
依据行星齿轮传动机构特性,提出双电动机耦合驱动系统构型,具体结构如图1所示.双电动机耦合驱动系统由1套行星齿轮机构、2个电动机(电动机M1、电动机M2)、离合器C1、离合器C2、制动器B1和制动器B2组成.其中2个电动机作为动力输入,电动机M2与太阳轮直接连接,电动机M1通过减速齿轮与齿圈连接,行星齿轮机构的动力由行星架输出,行星架与驱动桥直接连接.离合器C2可以控制齿圈和太阳轮之间的连接,离合器C1可以控制电动机M1的动力输出,制动器B1可以锁死齿圈,制动器B2可以控制电动机M2的输出,同时可以锁死太阳轮.

图1 双电动机耦合驱动系统构型
通过离合器C1、C2和制动器B1、B2的闭合状态实现4种耦合驱动工作模式,即电动机M1单独工作、电动机M2单独工作、双电动机转速耦合和双电动机转矩耦合,如表1所示.
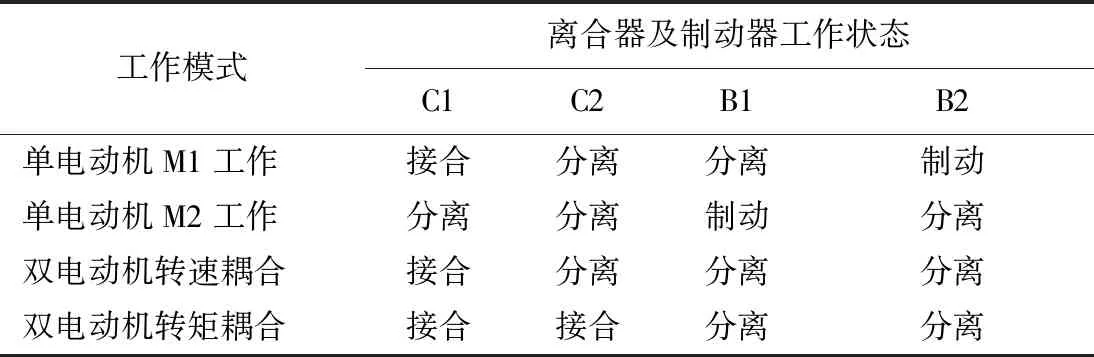
表1 双电动机耦合驱动系统工作模式
1.2 双电动机构型动力系统参数匹配设计
动力系统参数匹配首先依据车辆动力学指标进行整车参数匹配,然后通过对常用工况进行数理统计,对双电动机功能进行划分,进而确定双电动机参数.目标车型参数及动力性指标如下:整备质量为1 759 kg,满载质量为2 140 kg,迎风面积为2.2 m2,风阻系数为0.335,滚动阻力系数为0.015,轮胎半径为347 mm,轴距为2 800 mm,最高车速为170 km·h-1;100 km加速时间为8 s,最大爬坡度为30%(车速30 km·h-1).
基于多种典型循环工况对电动机参数进行匹配,匹配结果如表2所示.

表2 电动机参数匹配设计结果
2 双电动机耦合驱动系统控制策略
2.1 缺省控制策略
2个电动机均处于工作状态,输出的转矩为
(1)
式中:TM1、TM2分别为电动机M1和M2的输出转矩;Treq为需求转矩;k1、k2分别为电动机M1、M2的转矩分配系数.
将汽车行驶的需求转矩按转矩分配系数来分配2个电动机的输出转矩.
2.2 效率最优控制策略
2.2.1驱动系统效率
当驱动系统处在单电动机工作模式时,电动机的工作点由汽车行驶速度和基于行驶工况的需求转矩唯一确定,驱动系统效率也随之确定;当驱动系统处在转矩耦合工作模式时,由汽车行驶状态和传动系统参数可以确定2个电动机的转速,电动机工作转矩可以在转矩允许范围内任意组合;当驱动系统处在转速耦合工作模式时,由汽车行驶的需求转矩可以确定2个电动机的工作转矩,电动机工作转速可以在转速允许范围内任意组合.
首先按照车辆匀速直线行驶计算整车行驶驱动力Fr,即
(2)
式中:m为整车质量;g为重力加速度;f为滚动阻力系数;CD为风阻系数;A为迎风面积;u为车速;δ为整车质量换算系数.
驱动系统总效率为
(3)
式中:Pout为驱动系统输出功率;Pin为驱动系统输入功率;ωM1、ωM2分别为电动机M1和M2的角速度;ηM为双电动机工作总效率;ηt为驱动系统传动效率.
单电动机工作模式下,电动机工作转矩为整车需求转矩,转速由车速得到,则驱动系统总效率为
(4)
式中:Mi为电动机M1或M2;TMi、ωMi分别为单电动机的输出转矩和角速度;ηMi为单电动机工作效率.
在双电动机耦合工作模式时,在需求转矩和需求转速约束下,2个电动机工作点可以在允许范围内任意组合,利用序列二次规划优化算法,基于驱动系统效率最优原则,计算2个电动机的最优工作点,确定2个电动机的动力分配方案.驱动系统效率优化目标函数为
f(x)=maxηsys.
(5)
约束条件如下:
(6)
式中:PM1、PM2分别为电动机M1和M2输出的功率;SOCmin为电池最小荷电量;SOC为电池荷电量;Umin、Umax分别为电池输出的最小和最大电压;Ubat为电池输出电压;T1(ωM1)、T2(ωM2)分别为电动机M1和M2在相应角速度下输出的转矩;T1max(ωM1)、T2max(ωM2)分别为电动机M1和M2在相应角速度下输出的最大转矩.
2.2.2驱动系统效率最优工作模式
双电动机耦合工作模式时,由于2个电动机的工作点不具有确定性,因此以驱动系统效率最优为目标函数,在约束条件下,采用序列二次规划算法对电动机工作点进行寻优计算.将驱动系统效率最高的工作模式作为驱动系统的最优工作模式,通过计算可划分出双电动机耦合驱动系统的效率最优工作区域,得到工作点对应的工作模式如图2所示,其中nM1、nM2分别为电动机M1和M2的需求转速.
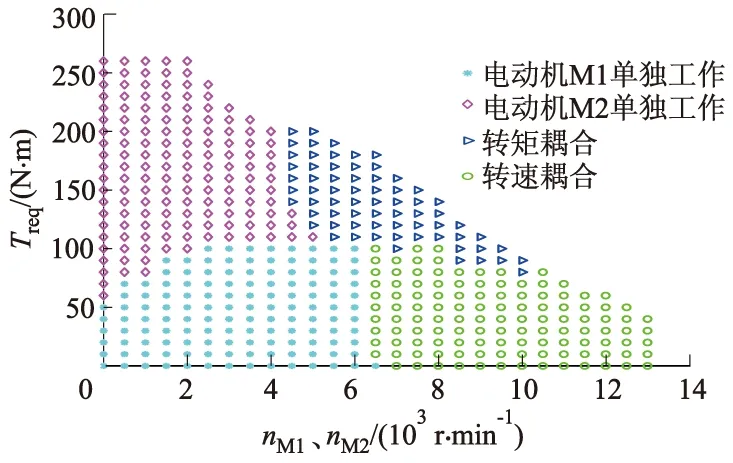
图2 双电动机耦合驱动系统模式切换示意图
从图2可以看出:当车辆有低速、较小转矩需求时,电动机M1单独工作;当车辆有低速、较大转矩需求时,电动机M2单独工作;当车辆有中速、较大转矩需求时,双电动机转矩耦合工作;当车辆有高速、较小转矩需求时,双电动机转速耦合工作.
由于采用瞬时模式切换算法,控制过程难,且计算繁琐,因此为了提升控制模型的决策效率,采用边界曲线将4个工作模式进行划分,然后将4个模式之间设置门限值,如图3所示.

图3 双电动机耦合驱动系统模式切换边界
将模式识别进行简化之后,建立模式识别控制策略.在完成模式识别规则制定后,在单电动机工作时,转矩以及转速需求直接分配给单电动机,在双电动机耦合工作模式下,依据最优控制算法求解的工作点,对电动机的转矩和转速进行分配.
2.2.3双电动机动力分配控制策略
依据2.2.2节求解的效率最优模式识别控制策略,在双电动机转矩耦合工作模式时,由于2个电动机工作点不确定,基于驱动系统效率最优原则分配2个电动机的转矩,驱动系统转矩耦合模式下的效率最优转矩分配控制策略的电动机M1和电动机M2的输出转矩特性如图4所示.

图4 转矩耦合模式下电动机输出转矩特性
在双电动机转速耦合工作模式时,基于驱动系统效率最优原则分配2个电动机的转速,驱动系统转速耦合模式下的效率最优转速分配控制策略的电动机M1和M2的输出转速特性如图5所示.其中no1、no2分别为电动机M1和M2的输出转速.

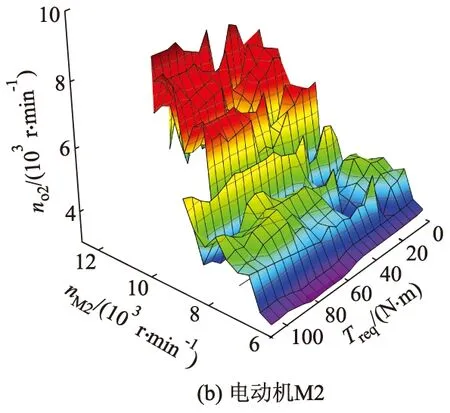
图5 转速耦合模式下电动机输出转速特性
3 驱动系统效率最优控制策略验证
利用AVL CRUISE软件建立纯电动汽车仿真模型[10],按照GB/T 18386—2017《电动汽车能量消耗和续驶里程试验方法》分别对电动汽车能量消耗、续驶里程进行经济性分析[11].在进行汽车能量消耗分析前,需要检测车速跟随情况,良好的车速跟随可以保证试验结果的准确性.选取NEDC(new European driving cycle)工况进行车速跟随仿真分析,如图6所示,其中:ua为目标车速;t为时间.结果表明仿真车速可以很好地跟随NEDC工况的车速,说明仿真模型满足试验精度,可以进行经济性能仿真分析.

图6 NEDC工况下车速跟随示意图
续驶里程测试采用NEDC和WLTC(world light vehicle test procedure)这2种常用循环工况进行测试.仿真试验之前在CRUISE中Initial Values中设置SOCTarget的控制方式,一般情况下,SOC的利用率为95%到5%,否则会影响电池使用寿命.能量消耗率一般采用100 km电耗来表示,计算方法为电池的输出能量除以测试行驶的续驶里程.在电池SOC可用范围下2种驱动方案下的续驶里程和100 km电耗水平如表3所示,在2种循环工况下,效率最优驱动控制方案,具有更高的续驶里程和更低的100 km电耗水平,相比于缺省控制方案有明显的性能提升.

表3 双电动机耦合驱动系统2种驱动控制方案的续驶里程和100 km电耗对比
3.1 电池输出特性对比分析
电池的SOC值为电池当前剩余的荷电量与完全充电状态下的荷电量的比值,SOC值的大小直接体现出电池储存能量的高低.在进行测试电池输出特性时,一般以单次工况消耗的电池电量作为衡量电动汽车能耗的标准.分别采取NEDC、WLTC单次循环工况进行测试,电池SOC初始值设定为60%,2种驱动控制方案下SOC的变化曲线如图7所示.
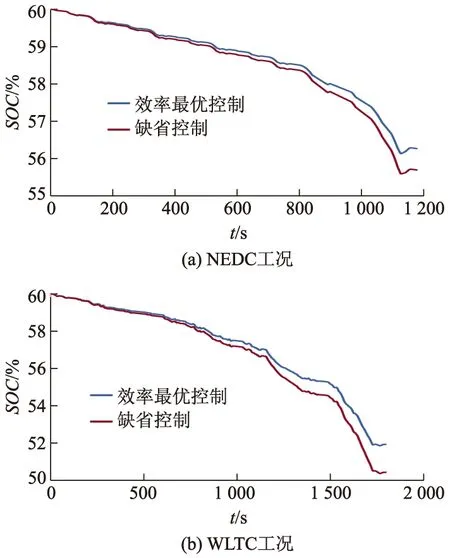
图7 2种驱动控制方案的SOC变化曲线
在NEDC工况下,缺省控制策略在完成单次循环工况时的SOC值为55.69%,驱动系统效率最优控制策略在完成单次循环工况时的SOC值为56.26%.在WLTC工况下,缺省控制策略在完成单次循环工况时的SOC值为50.43%,驱动系统效率最优控制策略在完成单次循环工况时的SOC值为51.93%.驱动系统效率最优控制策略相比缺省控制策略SOC曲线下降速率明显变缓,说明驱动系统效率最优控制策略能够提高电动机的工作效率,间接提高了电池能量的利用率,增强了整车的节能效果.
3.2 电动机输出特性对比分析
在不同的行驶工况和不同的控制策略方案下,电动机的工作特性也会不同.由于NEDC工况分为加速工况和匀速工况,并且车速平滑,便于仿真测试分析.一个NEDC工况由4个市区循环工况(urban driving cycle,UDC)和1个市郊循环工况(extra urban driving cycle,EUDC)组成.因此分别选取UDC工况和EUDC工况对电动机的输出特性进行研究.
对2种驱动控制方案的2个电动机输出转矩特性进行分析,UDC工况下2种驱动控制方案的电动机工作输出特性如图8所示,EUDC工况下2种驱动控制方案的电动机工作输出特性如图9所示.

图8 UDC工况下2种驱动控制方案的电动机输出特性

图9 EUDC工况下2种驱动控制方案的电动机输出特性
从图8可以看出:在缺省控制方案中,驱动系统一直保持双电动机工作模式;2个电动机转矩按比例进行分配,在加速工况,电动机输出转矩虽有小幅波动,但总体输出平稳;在匀速工况时,电动机输出转矩总体偏低.从图9可以看出:在效率最优控制方案中,在城市工况下,在车辆加速时电动机M1单独工作,当车速和转矩需求增加时,切换到电动机M2工作继续加速;在市郊工况下,在车辆高速行驶时,驱动系统处于转速和转矩耦合工作模式.
在UDC工况和EUDC工况下2种驱动方案的电动机驱动工作点分布分别如图10、11所示.

图10 UDC工况下2种驱动控制方案的电动机驱动工作点分布示意图
从图10可以看出:UDC工况下,双电动机耦合驱动系统效率最优驱动控制方案中,2个电动机负荷率较高,电动机工作点在高效区所占比例更大,电动机工作点分布更优,驱动系统效率提升明显.
从图11可以看出:EUDC工况下,效率最优驱动模式下的双电动机耦合驱动系统中2个电动机的负荷率较高,相比于缺省控制方案,电动机工作点在高效区所占比例更大;在加速工况和匀速工况中,电动机M2虽然工作效率略微下降,但电动机M1都工作在最佳效率区间内,使驱动系统效率得到更大提升;在整个NEDC循环工况中,双电动机耦合驱动系统平均效率为85.9%,在缺省控制驱动方案下驱动系统效率大于85.0%的电动机工作点占42.0%,在驱动系统效率最优驱动方案下驱动系统效率大于85.0%的电动机工作点占55.0%.结果表明,在驱动系统效率最优驱动方案时,电动机可以工作在较高的效率区间内,电动机的负荷率更高.

图11 EUDC工况下2种驱动控制方案的电动机驱动工作点示意图
4 结 论
1)依据行星齿轮传动机构特性,同时采用离合器与制动器来控制电动机的动力输出,提出双电动机耦合驱动纯电动汽车动力传动系统构型,并进行动力传动系统工作模式分析.
2)利用序列二次规划算法,基于驱动系统效率最优原则,计算2个电动机的最优工作点,确定2个电动机的动力分配方案,提出驱动系统效率最优控制策略.
3)建立纯电动汽车仿真模型,选取NEDC工况、WLTC工况下电池SOC变化曲线进行分析,结果表明驱动系统效率最优控制策略相比缺省控制策略SOC曲线下降速率明显变缓,提高了电池能量的利用率,进而增强了整车的节能效果.
4)选取UDC工况和EUDC工况,进行2种驱动控制策略下电动机工作特性分析,结果表明,在驱动系统效率最优驱动方案时,电动机工作在大于85.0%的效率区间内的工作点占55.0%,电动机的负荷率更高,驱动系统效率得到更大的提升.

