复杂船体结构拓扑优化中最小稳定拓扑板厚的快速确定方法

朱俊侠，吴嘉蒙*，刘亚冲，高明星

1 中国船舶及海洋工程设计研究院，上海 200011

2 上海市船舶工程重点实验室，上海 200011

1 引 言

近年来，结构优化成为了船舶结构设计领域的研究热点，优化的目的是在确保结构安全的前提下，尽可能减少结构重量，实现轻量化结构设计[1-2]。在常规的结构优化方法中，拓扑优化不同于尺寸优化或形状优化，其目标是寻找结构材料最优的分布形式及结构的最佳传力路径，使其能够较大程度地改善结构特性，而这是其他优化方法无法做到的[3-4]。

目前，船舶结构拓扑优化方法的应用研究还不够深入，尤其是针对复杂的船体结构，例如横向强框架、水平桁等。所谓“复杂”结构，不仅是指代结构型式，还体现在板厚分布方面。不同于机械三维实体零件，对船体结构开展拓扑优化设计时，其设计域单元类型多为二维板壳单元，也可以认为其是由多个二维设计域组合在一起的优化设计[5-7]。针对三维实体单元的拓扑优化，只需输入材料的密度，而针对二维板壳单元拓扑优化，还需确定设计域的板厚。因此，如何确定二维设计域的板厚，这是船体结构拓扑优化需要直接面对的一个问题。

对于结构型式简单的船体结构，若其初始结构的板厚是唯一的或数值相差不大，要求设计域板厚与初始结构板厚一致或相似即可。然而，对于比较复杂的船体结构，例如VLCC油船货舱内的横向强框架，在初始设计中就存在多个板厚，且最大值与最小值之间相差近10 mm。同时，强框架上还布置有防屈曲筋和面板，对其进行拓扑优化时设计域的板厚如何取值尚无准确的方法[8]。鉴于设计域板厚与设计域体积直接相关，板厚得不到确定将无法确定设计域体积，影响约束条件中体积分数约束值的确定，致使在目前船体结构拓扑优化实践中体积分数约束值通常需要依靠大量试算才能大致获得，缺乏可靠的确定方法。在体积分数约束值给定的前提下，本文作者在文献[1]中的研究发现，设计域板厚取值差异在复杂受力环境下将对横向强框架的拓扑构型产生影响，故针对不同设计域板厚的大量优化计算及多个工况的多组拓扑结果，提出了“最小稳定拓扑板厚”的概念，认为在各工况载荷下存在某个最小设计域板厚（即设计域板厚不小于该值时，横向强框架的拓扑优化构型相对稳定），并且基于该最小稳定拓扑板厚可进行稳定拓扑构型的工程化方案设计。但是，在通过逐个工况来确定最小稳定拓扑板厚的过程中需要依赖工程师判断构型的稳定性，且只能定性而无法定量给出判断，工作效率和自动化程度有待提高。

综上所述，本文将以横向强框架拓扑优化为例，进一步开展复杂船体结构的相关研究。基于初始横向强框架的体积，提出一种设定体积分数约束值的折衷方法，以及基于拓扑结果中的单元相对密度值，提出一种横向强框构型识别方法，并通过量化处理，减少人为判断因素的干扰，快速确定各工况下强框架的最小稳定拓扑板厚。

2 拓扑优化中体积分数约束值的一种确定方法

2.1 方法介绍

拓扑优化中常见的约束条件有体积分数约束、位移约束以及应力约束[9]。本文作者在文献[1]中提出，针对横向强框架的拓扑优化，约束条件应不设置应力约束，仅设置体积分数约束即可。但是，设计域板厚取值的不确定性会影响到约束条件中体积分数约束值的设定。

船体结构拓扑优化中体积分数约束值Cvf的设定一般需要参考初始结构的体积V0，并将V0与设计域体积Vdd之比Cvf0作为参考值。鉴于轻量化设计的目的，在实际结构优化时，Cvf取值可以适当小于Cvf0，即

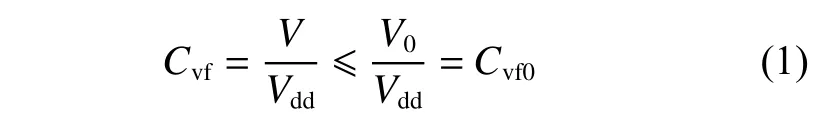
式中，V为优化后所保留的拓扑构型体积。

然而，如上所述，横向强框架的设计域板厚目前尚无准确的方法，即使设计域范围已确定，设计域体积Vdd依然无法确定，进而导致体积分数约束参考值Cvf0无法确定，体积分数约束值Cvf无设定依据，最终使拓扑优化较难开展。经研究认为，针对以横向强框架为代表的复杂船体结构，拓扑优化时Cvf的确定可以归结为Cvf0的确定问题，但是Cvf0确定的条件是设计域板厚已知。因此，可将式（1）中的所有体积项展开，写为式中：A为优化后所保留的拓扑构型面积；A0为初始结构的面积；Ad为设计域的面积；td为设计域板厚；taver为初始设计强框架结构的平均板厚。其他变量同式（1）。

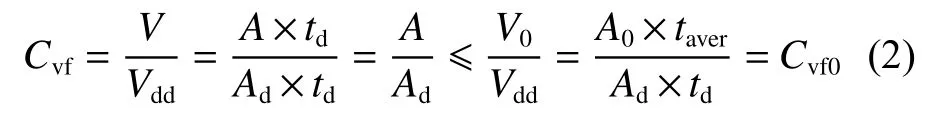
由式（2）可知，Cvf0的确定有2种方法：第1种是考虑td，根据自行取值的td，与初始设计强框架的平均板厚taver进行直接计算（以下称方法1）；第2种是不考虑td，仅将拓扑前、后的面积之比A0/Ad作为确定Cvf0的依据，即认为A0/Ad≈Cvf0，此时，Cvf0可唯一确定（以下称方法2）。

进一步分析发现：方法1尽管能够同时考虑td和taver，但其致命的问题是Cvf0会随着td的变化而变化，无法唯一确定；而方法2可以确保Cvf0的唯一性，但此时td的影响无法考虑，其结果将完全依靠拓扑前、后的面积之比A0/Ad来确定。经研究认为：拓扑优化的最终目的在于寻找到设计域内最佳/主要的载荷传递路径，关注的重点应是设计域的最终拓扑构型；在板厚均匀的二维设计域上，结构的构型在一定程度上可由面积分布情况来决定。因此，将拓扑结构的体积之比退化为其面积之比是可以接受的。至于设计域板厚对拓扑结果的影响，可以通过同一体积分数约束值下多组设计域板厚的拓扑结果进行判断。因此，综合上述分析，本文认为方法2更为可行。

2.2 实船算例的验证与分析

为了进一步验证上述2种方法的合理性，以某型VLCC油船货舱内典型强框架的拓扑优化为例，按照上述2种不同方法取值，分别给出体积分数约束值Cvf的拓扑结果。本文所有拓扑优化计算是基于固体各向同性惩罚微结构（solid isotropic microstructures with penalization，SIMP）的变密度法在HyperWorks/OptiStruct软件平台上完成的。优化工况为《双壳油船和散货船协调共同结构规范（HCSR）》[10]中三舱段模型强度分析规定的载荷工况，共42种。优化模型的具体尺寸信息详见文献[1]。本文仅给出了拓扑优化目标横向强框架所在位置以及强框架拓扑优化设计域设定的示意图，如图1和图2所示的黄色区域。拓扑优化的工况在本节选择为A1_HSM1_S（其中，A1为装载模式，HSM1_S为设计波工况）。

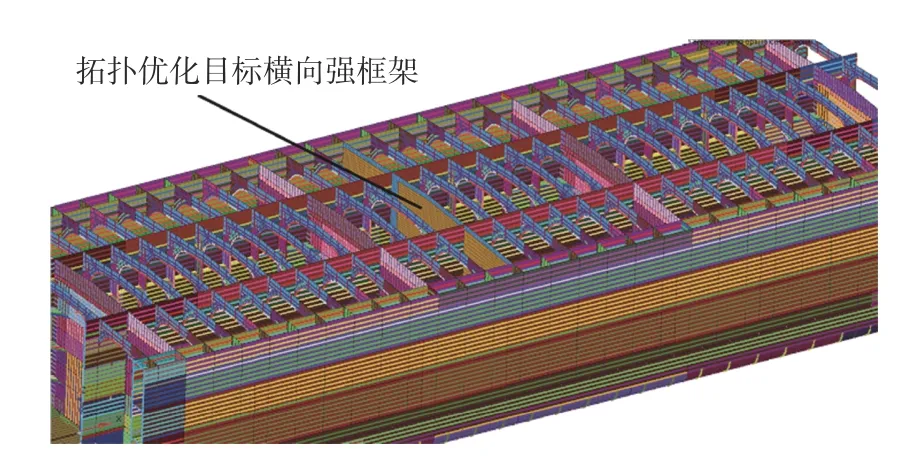
图1 拓扑优化目标横向强框架所在位置Fig.1 Location of target transverse web frame for topology optimization

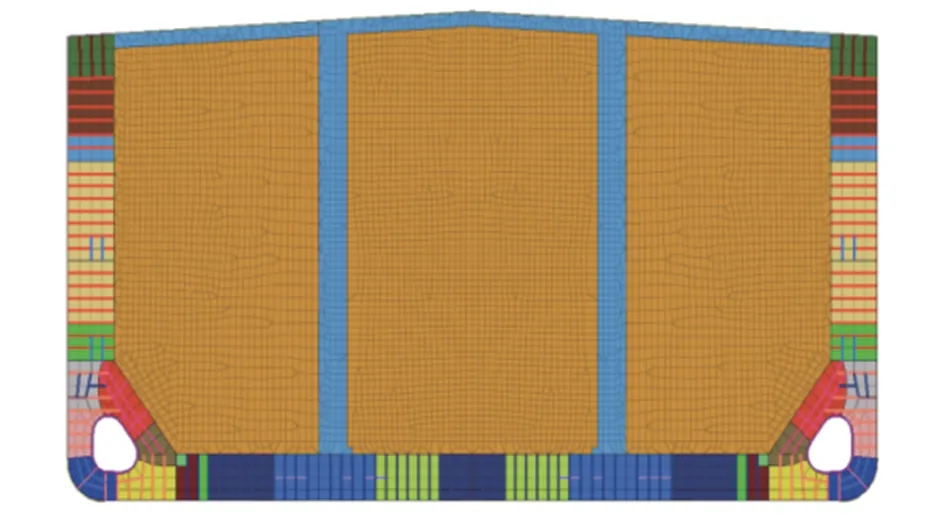
图2 横向强框架拓扑优化设计域Fig.2 Design domain of transverse web frame for topology optimization

1） 通过td和taver（23 mm）计算体积分数约束参考值Cvf0。

在表1中给出了一系列横向强框架的td值，采用方法1分别确定Cvf0，在约束条件中暂取Cvf等于Cvf0，具体数值如表1第2列所示。表中，x表示单元相对密度的阈值。

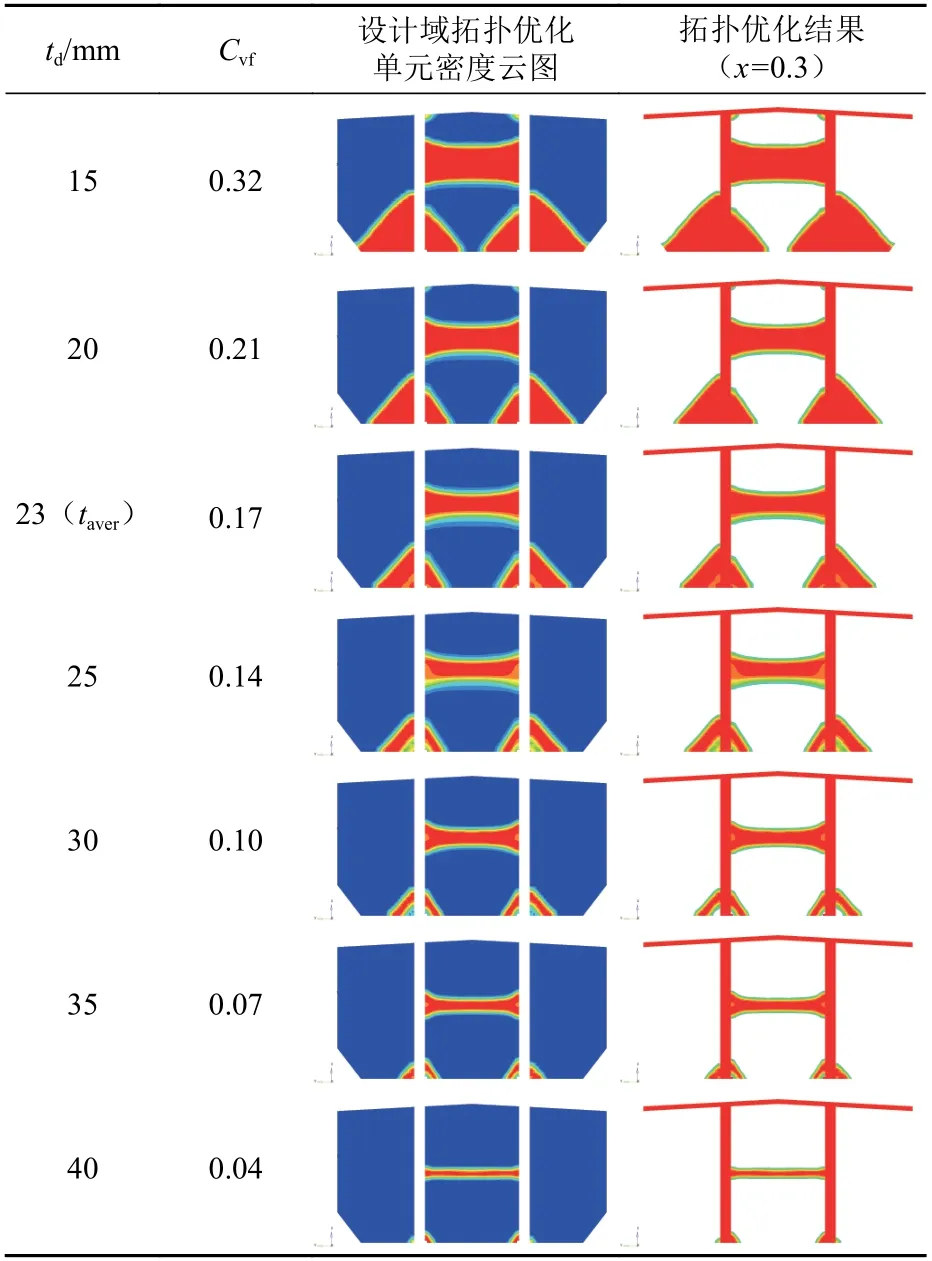
表1 不同设计域板厚与对应体积分数约束值下的横向强框架拓扑优化结果Table1 Topology optimization results of transverse web frame constrained by different plate thickness of design domain and corresponding volume fraction

由表1可知，采用方法1确定体积分数约束值时，td取值对Cvf影响较大。例如，td从20 mm变为30 mm时，Cvf由0.21减至0.10，此改变对最终的拓扑结果会产生很大影响。因此，为将此影响可视化，基于上述td与Cvf分别开展了目标横向强框架的拓扑优化。优化的数学模型如下：

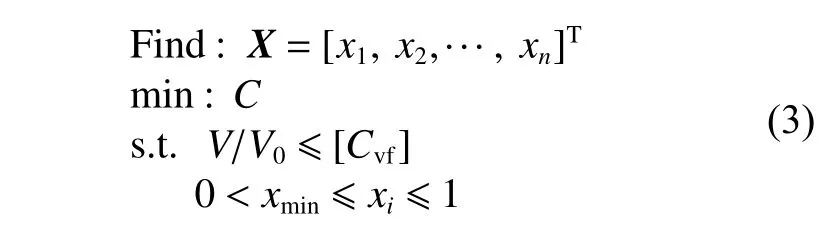
式中：X为设计域内各单元的相对密度；C为单工况三舱段结构柔度值；[Cvf]为指定的体积分数约束值；xmin为设计域内单元相对密度的最小值，通常取为0.001。

根据表1第3与第4列给出的不同td与Cvf所对应的横向强框架拓扑优化结果可见，当td在小范围内变化时，对拓扑优化结果的影响不明显，例如td为20，23与25 mm时的结果；当td的变化范围增大时，例如由20 mm变为30 mm，Cvf则由0.21减至0.10，此时，对拓扑结果的影响开始显现，不仅横撑的面积缩减，纵舱壁上的垂直桁与内底的相交结构也由大肘板变为了斜撑；当td的变化范围继续增加时，例如由20 mm变为40 mm，Cvf则由0.21减至0.04，此时，对拓扑结果的影响特别明显，横撑的面积急剧缩小，同时内底板上的大肘板基本消失。

由上述分析结果可见：当td变化时，若Cvf也随之改变，则td的取值对拓扑结果起着至关重要的作用；若取值不合适，就无法获得理想的拓扑构型；另外，若试图通过本方法不断调整td来获得Cvf值，则需要对比多组拓扑结果，这不仅对工程师的优化设计经验有一定的要求，而且也很难获得精度较高的Cvf值。

综上所述，通过理论分析与算例验证，本文认为采用方法1确定Cvf并不理想。

2） 通过面积比A0/Ad确定Cvf0。

该方法在确定体积分数约束参考值Cvf0时，暂不考虑td的影响，而以面积比A0/Ad作为依据。其实，该比值也等同于方法1中td=taver的计算结果。经计算后可知，Cvf0=A0/Ad= 0.17。作为对比，表2给出了相同Cvf（Cvf= 0.17）时不同td的拓扑优化结果。

由表2所示结果可见，在A1_HSM1_S工况下，当td从15 mm变化至40 mm时，横向强框架的拓扑构型基本稳定，拓扑构型的面积也近似，没有出现如表1中所示拓扑构型变化较大的现象。通过该方法确定Cvf可以暂时跳过确定td这个难题，同时依然可以获得较为理想的拓扑构型。接下来，可以在相同Cvf下开展td对拓扑优化结果的影响研究，进而给出td的取值建议或者方法，即将确定td的问题放在后续阶段予以研究。因此，本文认为方法2是一种较为合理的方法，建议作为确定Cvf的方法。

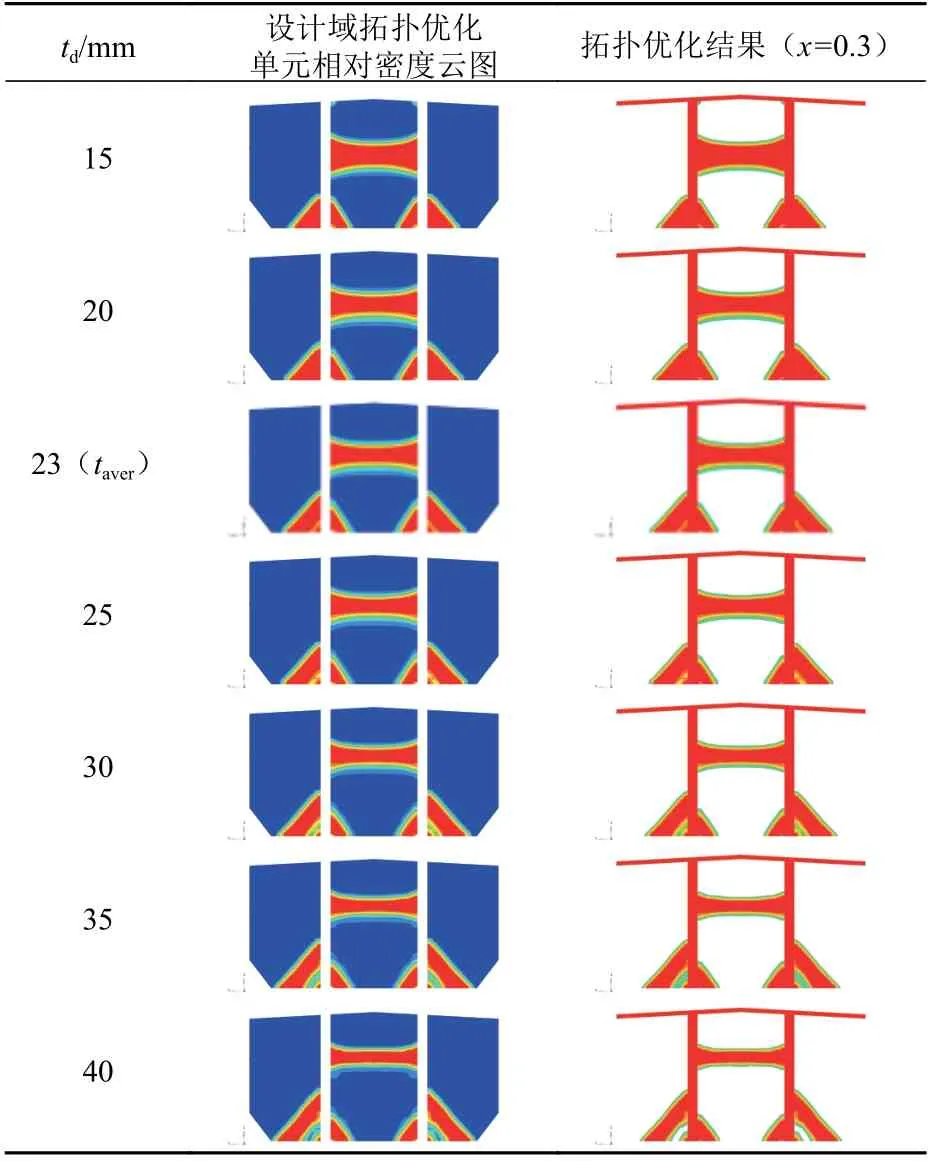
表2 相同体积分数约束值（Cvf = 0.17）下不同设计域板厚所得拓扑优化结果Table2 Topology optimization results with different thickness of design domain under the same volume fraction constraint (Cvf = 0.17)

综上所述，复杂船体结构的td目前无法确定且Cvf与td之间存在密切的联系，通过分析拓扑优化的目标，本文对初步提出的2种Cvf确定方法进行了选优，以船体结构典型强框架的拓扑优化为实例，对优化结果进行对比，最终给出了确定Cvf的折衷方法。

3 拓扑优化设计域最小稳定拓扑板厚的确定方法

3.1 一般性确定方法

对于复杂船体结构的拓扑优化，在td尚无法确定时，需要对其开展优化结果的影响研究。本文作者在文献[1]中详细给出了某型VLCC油船货舱内典型横向强框架在15种工况下不同td的拓扑结果，基于多组拓扑结果分析，提出了“最小稳定拓扑板厚”的概念。

限于篇幅，本文仅给出了文献[1]中较具代表性的2种工况下的横向强框架拓扑结果，具体如表3和表4所示。开展优化的数学模型如式（3）所示，出于轻量化设计的考虑，Cvf取值为0.12。

通常，最小稳定拓扑板厚的确定是基于拓扑构型识别方法。随着td由小到大地递增，拓扑构型开始稳定时其所对应的最小td即为“最小稳定拓扑板厚”。根据表3和表4的拓扑结果，两种工况下的最小稳定拓扑板厚分别为15 （仅从构型上判断，甚至10 mm也可以）和23 mm。目前，关于拓扑构型是否趋于稳定的判断，需要依靠工程师的经验，这不利于提高工作效率。同时，在有些工况下，例如A1_HSM1_S工况，最小稳定拓扑板厚为15和10 mm时所对应的拓扑结果相差并不明显，在此工况下的最小稳定拓扑板厚其实并不好作出判断。

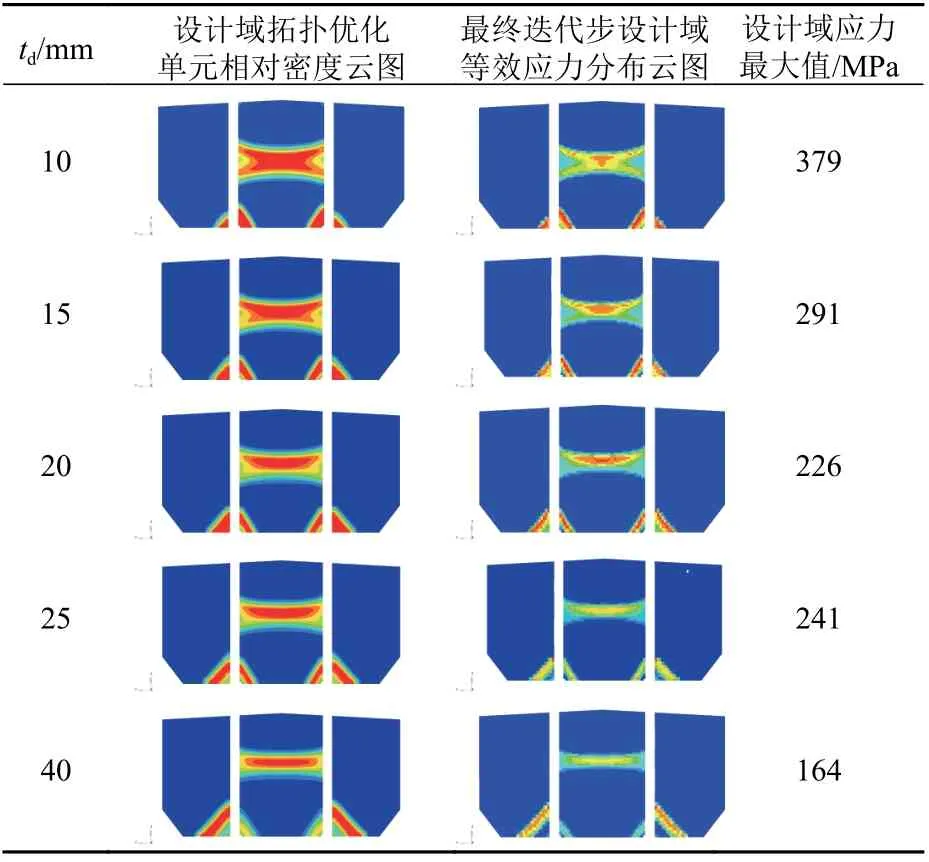
表3 A1_HSM1_S工况下不同设计域板厚所得拓扑优化结果Table3 Topology optimization results of different plate thicknesses of design domain in the load case of A1_HSM1_S

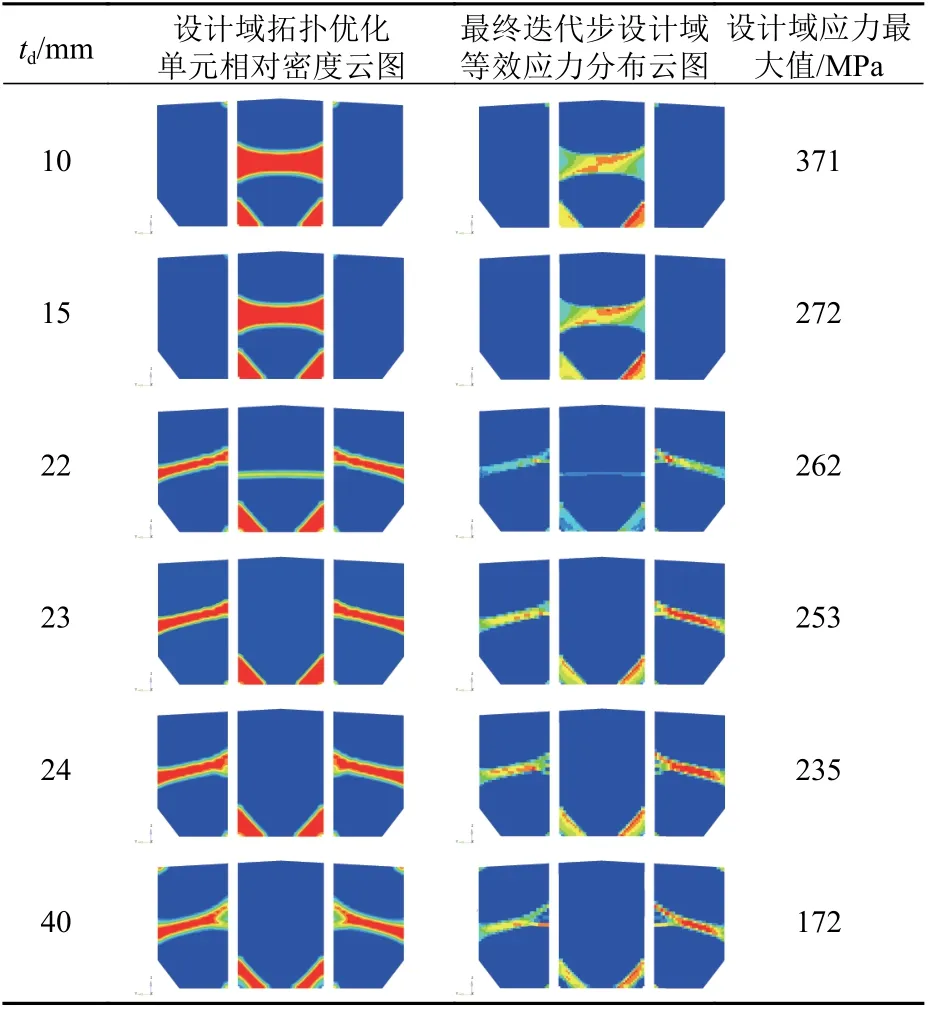
表4 A2_BSR1P_S工况下不同设计域板厚所得拓扑优化结果Table4 Topology optimization results of different plate thicknesses of design domain in the load case of A2_BSR1P_S

因此，需要采用一种构型识别方法来自动判断构型是否趋于稳定，进而确定各工况下的最小稳定拓扑板厚。通过该方法对构型判断问题予以量化处理，并在保证一定的准确性前提下，减少工程师的人为判断，从而提高优化效率。

3.2 基于单元统计的设计域最小稳定拓扑板厚确定方法

从上述表中多组强框架的拓扑结果可以发现，40 mm的td远大于各工况下的最小拓扑稳定板厚，且此时的拓扑构型都较为合理。因此，可将40 mm的td对应的拓扑构型作为参考构型。若相同工况下其他td的拓扑构型与该参考构型相似，即可以认为其也是稳定的拓扑构型。由此，横向强框的设计域最小拓扑稳定板厚的确定问题可以转化为：参照强框架td=40 mm时所对应的稳定拓扑构型，寻找可达到稳定拓扑构型的最小td。

通过对该型VLCC油船货舱典型横向强框架多组拓扑优化的试算，可以发现强框架拓扑构型大致可以分为3种：第1种为横撑布置在中间舱，内底设有肘板或斜撑；第2种为横撑布置在两个边舱，内底设有肘板或斜撑；第3种为横撑同时布置在中间舱与边舱，内底设有肘板或斜撑，该构型可认为是第1和第2种构型的过渡型式。上述3种构型最关键的差别在于横撑位置，只要获取拓扑结果中的某个参数，且能够有效区分构型间的差异，即可作为构型对比的依据。在拓扑结果中，单元相对密度云图是提取拓扑构型最重要的依据，单元保留与否是通过单元相对密度来判断的，即单元相对密度越高，表明该单元越重要，应予以保留，而单元相对密度越低，表明该单元越不重要，可以予以舍弃。因此，可将设计域划分为若干个子区域，对两种构型进行对比，若每个区域内保留的高密度单元数量都相差无几，即可认为两种构型是相似的。通过观察横向强框架的上述3种拓扑构型，可以发现不同区域内高密度单元数量有着较明显的差别。基于此特性，本文将强框架设计域划分为如图3所示的左、中、右3个区域（分别对应于红、蓝、黄区域），然后，统计各自区域内的相对密度大于0.34的单元数量，将其作为该区域内结构分布情况的一种指标。由于在拓扑优化时，通常会设置设计域左右对称的工程约束，因此左、右两个区域的结果相同，任选一边即可。本文选择的是左边区域的结果。

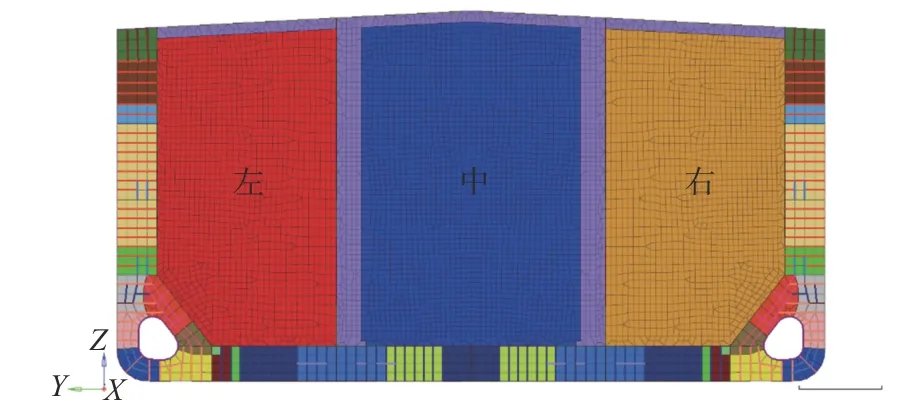
图3 横向强框架设计域分区示意图Fig.3 Distribution of design domain in transverse web frame

构型识别的具体步骤如下：

1） 开展n个工况下不同设计域板厚的拓扑优化计算，分别读取各工况不同设计域板厚的拓扑结果。

2) 分别统计i（i≤n）工况设计域板厚为40 mm时左边与中间区域内单元相对密度大于0.34的单元数量num_port_40与num_mid_40。

3) 设置初始的设计域板厚X= 9 mm。

4）X=X+1。

5） 分别统计i工况设计域板厚为X时左边与中间区域内单元相对密度大于0.34的单元数量num_port_X与num_mid_X。

6） 左边区域统计结果的对比。若num_port_40 ＞100，则计算w_port_X=num_port_X/num_port_40，在满足0.7 ≤w_port_X≤1.4时，进入步骤7），否则返回步骤4）；若num_port_40 ≤ 100，在满足num_port_40 – 60 ≤num_port_X≤num_port_40 + 60时，进入步骤7），否则返回步骤4）。

7） 中间区域统计结果的对比。若num_mid_40 ＞100，则 计 算w_mid_X=num_mid_X/num_mid_40，在满足0.7 ≤w_mid_X≤1.4时，进入步骤8），否则返回步骤4）；若num_mid_40 ≤ 100，在满足num_mid_40 – 60 ≤num_mid_X≤num_mid_40 + 60时，进入步骤8），否则返回步骤4）。

8） 输出i工况下设计域最小稳定板厚为ti=X。

9） 判断i≥n是否成立，若成立，则输出n个工况下横向强框架的最小稳定拓扑板厚为t=max{t1,t2，···，tn}；若不成立，则i=i+1，返回步骤2）。

上述步骤中的各项指标限定范围是通过分析处理不同工况下各板厚的拓扑结果得到的，是各项指标的包络值。

为验证上述方法的可靠性，在表5中给出4种工况下（A1_HSM1_S，A1_FSM2_H，A2_BSR1P_S以及A2_HSM1_S）部分设计域板厚的参数统计结果。限于篇幅，未列入其他工况的结果。

根据表5中的数据，采用本节提出的构型识别方法进行判定，4种工况下的设计域最小稳定拓扑板厚ti分别为15，24，23和11 mm。而采用3.1节所提的一般性确定方法，需要结构工程师直观地对比各设计域板厚所对应的拓扑构型。当拓扑构型不再出现较大范围变化时，其所对应的设计域板厚即为该工况下的设计域最小稳定板厚。对比由工程师人为判断的结果与采用本节所提方法获得的结果，二者是一致的。除上述4种工况外，其他工况下的判定结果也是一致的，具体结果不再逐一列出。

综上所述，可以认为借助基于单元统计识别拓扑构型来确定复杂船体结构设计域最小稳定拓扑板厚的方法是有效的。该方法可以将最小稳定板厚确定问题进行数字化定量处理，一定程度上取代了结构工程师的人为判断需要，从而可以较快速地获取最小稳定拓扑板厚。同时，本文所提方法的流程清晰且指标具体，有利于运用计算机语言实现自动化处理，提高结构工程师优化工作的效率。

4 结 语

本文基于变密度的拓扑优化理论及Hyper-Works/OptiStruct优化平台，以VLCC油船货舱内横向强框架为例，针对复杂船体结构二维板壳单元设计域板厚取值差异会影响体积分数约束值的设定和稳定拓扑构型的获得等问题开展了分析研究，提出了一种设定体积分数约束值的折衷方法以及基于单元统计来识别构型并确定最小稳定拓扑板厚的方法。

研究结果表明：本文提出的体积分数约束值设定方法能够在尚无法确定设计域板厚的情况下，不依靠大量试算即可获得较可靠的体积分数约束值；基于单元统计的构型识别法有利于将构型识别问题进行数字化和程序化处理，一定程度上能够摆脱对工程师经验的依赖；同时，所提构型识别法能够快速确定相关工况下的设计域最小稳定拓扑板厚，为后续将该问题纳入复杂船体结构拓扑优化的自动化流程提供了解决方法。另外，本文研究成果还进一步完善了横向强框架拓扑优化研究的内容，可以为其他基于二维板壳单元的复杂船体结构拓扑优化问题提供思路和方法借鉴，具有重要的工程应用价值。