基于多约束二维排样的舰载机最大密度布列算法

林信海，杨大鹏，巩常兰，李文学

1 中国舰船研究设计中心，湖北 武汉 430064

2 华中科技大学 机械科学与工程学院，湖北 武汉430074

0 引 言

舰载机是航空母舰（简称“航母”）的主要作战力量，搭载更多数量的舰载机对提升母舰作战效能具有重要意义[1]。考虑到航母甲板空间有限，需在满足作战性能要求的前提下，对舰载机开展小型化设计，并优化其外形轮廓，来提高搭载舰载机的数量和上舰适配性[2]。为量化评估某型舰载机在航母飞行甲板和机库占地面积的指标，美海军基于近百年的航母舰载机使用经验，提出了“最大密度布列因子”这一指标[3-4]。

“最大密度布列因子”简称“布列因子”，是可有效表征停放某型舰载机所需占用飞行甲板和机库空间的一个经验指数，布列因子越大，表明舰载机占用的航母甲板面积越大。舰载机布列因子的计算流程具体如下[5]：

1） 设定F/A-18C飞机为基准舰载机，并规定其布列因子为1。

2） 按指定规则和约束，用基准舰载机填满“尼米兹”号航母的飞行甲板（不含着舰区）和机库，记录飞行甲板、机库布列飞机数量之和，设其为a。

3） 按同样规则布列某型舰载机，记录布列舰载机的总架数，假设为b。

4） 基准舰载机布列总架数和某型舰载机布列总架数的比值，即a/b，就是某型舰载机的布列因子。

舰载机最大密度布列是布列因子计算的核心，目前国内外舰载机最大密度布列通常由具有经验的人员借助CAD软件手工完成，设计周期冗长且要耗费大量人力，导致舰载机布列因子计算效率低下，因此，急需一种可快速自动生成舰载机最大密度布列方案的算法。

舰载机最大密度布列问题可归属于多约束条件下的二维不规则物体排样问题[6]。由于二维不规则物体排样问题的解空间较大，早期研究人员主要通过拼接和组合方式，将其转化为较易处理的规则多边形排样问题[7-8]，但利用该方法对极不规则物体进行排样时，易造成较大浪费。为此，Adamowicz等[9]基于多边形表示法，提出临界多边形（NFP，no fit polygon）算法，通过计算不规则多边形的NFP来判定多边形之间是否干涉。张思[10]采用基于重心NFP算法开展了舰载机自动布列软件的设计，但并没有考虑舰载机最大密度布列时的多个约束条件。

基于上述情况，本文将以二维排样算法为基础，重点研究舰载机最大密度布列多个约束条件的数学表达、处理策略及基本计算，并分别提出飞行甲板和机库最大密度布列算法。

1 舰载机最大密度布列约束条件概述

通常来讲，与常规的二维排样算法相比，舰载机在飞行甲板和机库最大密度布列要满足以下约束条件：

1） 距离约束。为满足布列安全要求，舰载机之间、舰载机与母舰边界/船体结构之间要保证一定的安全间距。其中，舰载机与母舰边界/船体结构的距离又包括机与舰外边界（如甲板边界、安全停机线）的距离、机与船体结构（如岛式上层建筑、机库壁、机库防火分隔门等）的距离，根据舰载机布列转运要求，舰载机之间、舰载机和岛式上层建筑等的间距不一样。

2） 超边界约束。舰载机身与船体结构、飞行甲板安全停机线应保持一定安全间距，不可发生干涉。但是，在靠近飞行甲板舷边布列时，在保证舰载机轮与甲板边缘有一定安全间距的前提下，舰载机机身可超出甲板边缘，即在布列时需动态考虑舰载机的外形边界。

2 舰载机最大密度布列的数学表达

2.1 舰载机、飞行甲板和机库的几何表达方法

舰载机、飞行甲板和机库外形轮廓均属不规则图形，其几何表达涉及到图形的存储、判交、平移、旋转等相关操作，直接影响到布列算法的耗时和精度。目前，主要采用以下方法来表达二维不规则形状：原始曲线表达法、多边形表示法和包络法等。本文选用多边形表示法进行舰载机、飞行甲板和机库的几何表达。

多边形表示法是指采用连通多边形的形式表达参与布列的甲板和舰载机图形，若舰载机、甲板轮廓存在曲线边，则根据一定的精度将曲线边近似成直线段来替代，如图1所示。

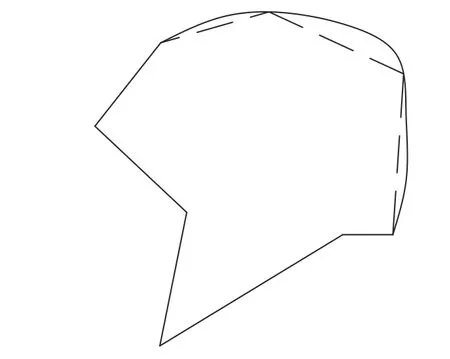
图1 多边形表示法Fig.1 The polygon-based representation

连通多边形的定义如下。

定义1：平面连通N边形P是指N个矢量端点的有序集合。以上矢量端点头尾相连并按逆时针（顺时针）方向排列，且各矢量之间不发生内点相交。

其数学表达式为P={P1(X1,Y1),P2(X2,Y2),···,Pi(Xi,Yi),···Pn(XN,YN),i=1···N}。

多边形表示法降低了图形之间的操作运算量，提高了排样速度。虽然在一定程度上会导致不规则图形精度的降低，但只要离散精度足够高，就能够满足布列精度需求。

2.2 距离约束数学模型及处理策略

如图2所示，将距离约束划分如下：l1为舰载机的间距，l2为舰载机和母舰外边界的间距，l3为舰载机和岛式上层建筑等母舰内边界的间距。

图2 二维排样中的距离约束Fig.2 The distance constraints of two-dimensional shapes nesting

本文采用等距缩放的策略来处理该距离约束，即对舰载机、甲板的边界按照一定间距进行放大或者缩小，再开展最大密度布列。设舰载机的实际间距为l′1，母舰内、外边界的实际间距分别为l′3和l′2，具体见式（1）。之后舰载机以间距l′1将边界进行放大；甲板以间距l′2将外廓进行等距收缩，以间距l3′将内廓进行放大。

之后，利用分段偏移法对舰载机和母舰进行等距处理，具体流程如下：

步骤1：将舰载机、母舰边界的每条线段均按等距方向进行等距操作。如图3所示，线段的起始端分别为Ps(xs,ys)和Pe(xe,ye)， 法向量为n，间距为d。进行等距处理后线段起始点为和，为点Ps到Pe的有向线段，则

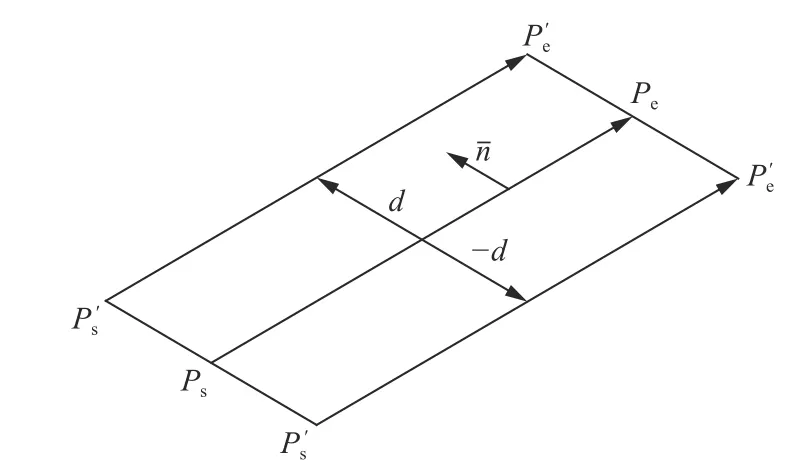
图3 直线的等距计算Fig.3 The offset calculation for lines

步骤2：对等距操作后得到的边缘进行封闭处理。等距操作后多边形相邻两边Ci与Ci+1如相交，需对其进行剪裁；如相离，需将其连接至一起，如图4所示。

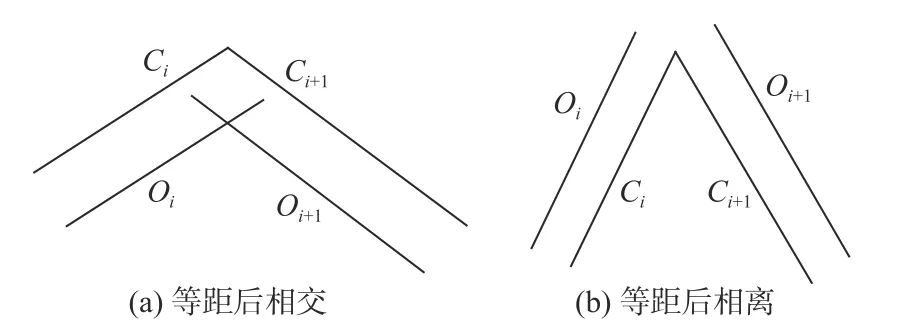
图4 线段等距后几何关系Fig.4 Geometric relation of lines after offsetting operation

本文采用直线延长的方式对相离两线段进行连接（图5）。

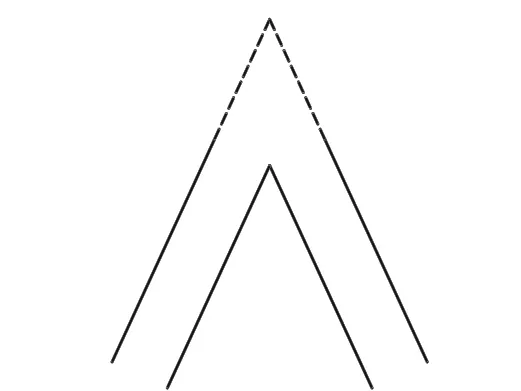
图5 线段的直线连接方式Fig.5 Connecting operation between lines

步骤3：对生成的原始等距边界进行检查，删除无效的边界，获得最终有效边界。

2.3 超边界约束数学模型及处理策略

飞行甲板上排样存在超边界的约束条件，二维超边界排样问题可表述为：一组二维不规则外形的零件P1,P2,···,Pn， 每个零件包含特征点{D1,D2,···,Dm}。需基于以下约束条件，在样板P中以最大密度排放以上零件P1,P2,···,Pn，需满足：

1） 任一零件Pi，Pj互不干涉。

2） 零件Pi的特征点{D1,D2,···,Dm}与样板P的外边界保持一定间距。

图6是舰载机超边界摆放的情况，即舰载机的机身边界可以超出飞行甲板停放，只要舰载机的机轮（通常为1个前轮和2个主轮）等特征点未超出飞行甲板边界即可。

图6 舰载机超边界布列方案Fig.6 Aircraft spotting plan under the constraint of overlapping the boundary

传统的排样算法无法满足超边界排样计算需求。考虑到可将样板分为飞行甲板边缘处的超边界排样区域和甲板内的常规排样问题，可采用不同的算法对其按先后次序进行计算。如先排布甲板边缘、再排布甲板内部，则为外围收缩次序；如先排布甲板内部，再排布外板，则为中心膨胀次序（图7）。

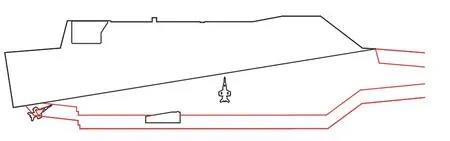
图7 甲板不同区域情况Fig.7 The different regions of flight deck

本文采用的外围收缩排样顺序可概括为：在飞机机轮不超出甲板边界的前提下，将飞机尽可能多地向甲板边缘和最小重心点移动，依次将飞行甲板外边界布满飞机，再开始对甲板内部区域进行飞机排布。

综上所述，超边界布列的定位步骤为：

1） 利用某图形格式导入飞机和飞行甲板的外形边界信息，在飞机图形中以不同图层标识飞机的特征点。

2） 获取飞机的特征点，根据特征点是否超出甲板区域，判定飞机是否越过边界。

3） 基于外围收缩顺序进行排样，即先进行飞行甲板边缘的飞机布列，再进行甲板内部区域的飞机布列。

3 机库舰载机排样算法

舰载机在机库内的最大密度布列可视为非等距约束下的不规则物体二维排样算法，其优化目标就是使机库内舰载机数量最大化。本文拟基于最低重心NFP算法[11]对其进行处理，机库最大密度布列算法流程图如图8所示。

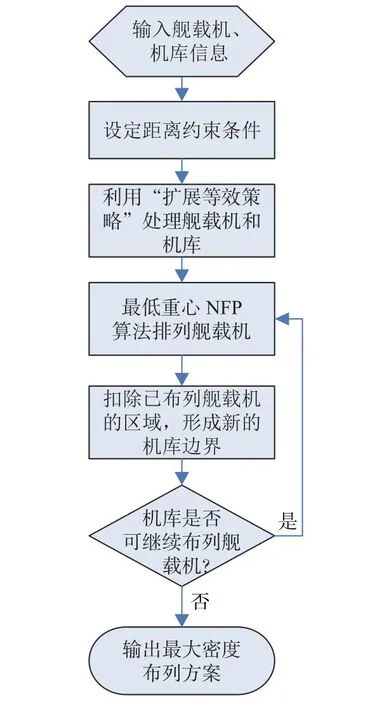
图8 机库最大密度布列流程图Fig.8 The workflow of maximum density spotting plan on the hangar deck

机库最大密度布列算法的步骤为：

1） 利用.dxf格式导入飞机和机库外形边界信息，并利用多边形表示法将其转化为离散点。

2） 根据最大密度布列准则要求，分别输入飞机之间，飞机与机库防护分隔门、机库壁的间距。

3） 基于式（1）和式（2），利用扩展等效策略处理舰载机和机库边界。

4） 利用最低重心NFP算法布列舰载机。最低重心NFP算法的排样规则将飞机放在重心最低的位置。其出发点是在不产生干涉的前提下，使布列舰载机的重心最低，为后面布列的舰载机留出更多的布列空间。其步骤为根据飞机外形边界得出其重心；然后以指定的角度间隔（本文为1°）旋转飞机，求解各旋转角度下的重心NFP，记录最低重心位置及对应的旋转角度，对飞机进行定位。采用最低重心NFP方法，获得最低重心的示意图（图9）。

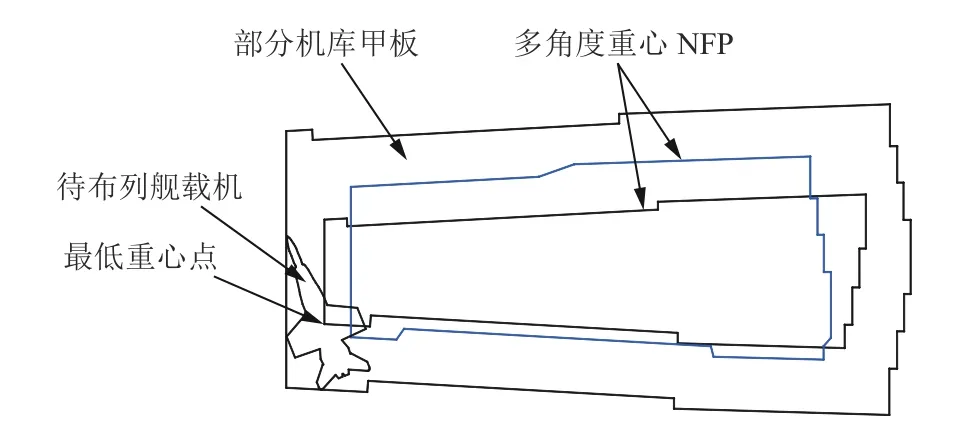
图9 最低重心NFP算法Fig.9 Lowest-gravity-center NFP algorithm

5） 从机库甲板上除去已布列飞机的面积，获得新的机库轮廓（图10），再进行下一步布列。

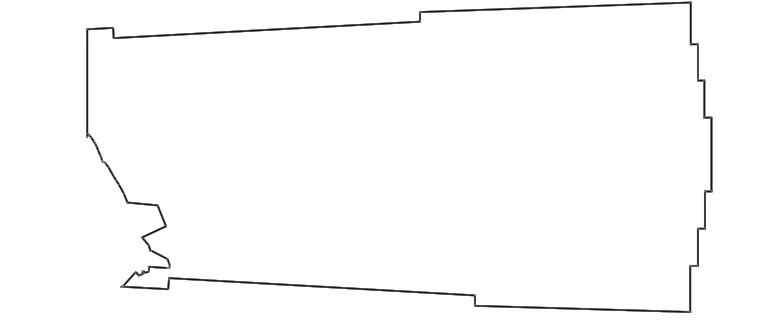
图10 新机库边界的合成Fig.10 Regeneration of the hanger deck contour

6） 重复以上步骤，直至剩余的机库空间不足以容纳1架飞机为止。

4 飞行甲板舰载机排样算法

针对飞行甲板舰载机最大密度布列，本文基于外围收缩顺序[12]，分别对飞行甲板边缘和内部依次按最大密度排布的方式进行计算。首先利用启发式靠边定位算法对甲板边缘处的飞机进行布列，直到飞行甲板边缘无法超边界布列飞机；然后采用机库最大密度布列飞机的NFP算法，对飞行甲板内部的飞机进行排样，直到甲板内布满飞机。飞行甲板舰载机排样的算法流程如图11所示。

图11 超边界约束下的舰载机布列算法流程图Fig.11 The algorithm workflow for aircraft spotting under the constraint of overlapping the boundary

启发式靠边定位算法的主要思想为：对于边L1（图12），将甲板的最左最下位置作为“零件局部最优”位置，沿L1的反方向采用该定位策略逐一布列舰载机，直至沿该方向无法布列舰载机为止；之后先后沿L2～L4的反方向采用类似的方式放置剩下的舰载机，只不过它们的“零件局部最优位置”则分别更新为最右最下位置、最右最上位置、最左最上位置，最终完成甲板边缘所有舰载机的布列。

图12 启发式靠边定位算法流程图Fig.12 The workflow of heuristic algorithm for keep-to-the-boundary spotting

基于该算法的飞行甲板边缘舰载机最大密度布列的具体步骤如下（图12）：

1） 以飞行甲板的艉部最右侧为起点，沿着右侧甲板边缘，按自艉向艏的方向，基于最艉最右位置为“零件局部最优”位置为原则开始布放飞机，直到该方向无法布列飞机。

2） 沿着艏部、左舷等甲板边缘，分别基于最艏最右、最艏最左位置为“零件局部最优”位置，完成飞行甲板边缘舰载机的布列。

5 算法实验结果

利用上述算法对F/A-18C飞机进行最大密度布列（图13），其中飞行甲板和机库的外形尺寸及边界根据文献[13]确定，飞行甲板和机库分别布列了76架和53架，总计129架飞机，与美军公布的飞行甲板和机库可最大密度布列130架F/A-18C飞机[14]基本吻合。

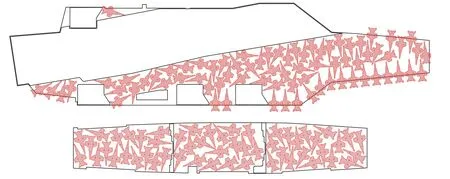
图13 F/A-18C飞机在飞行甲板和机库的最大布列图Fig.13 Maximum spotting pattern of the F/A-18C aircraft on the flight and hangar deck

以F/A-18C飞机为基准舰载机，对F-35C飞机进行最大密度布列（图14），飞行甲板和机库分别布列了69架和46架机，即可最大布列115架F-35C飞机，根据定义，其布列因子为1.12，与美军公布的F-35C飞机布列因子[4]为1.11基本相当。

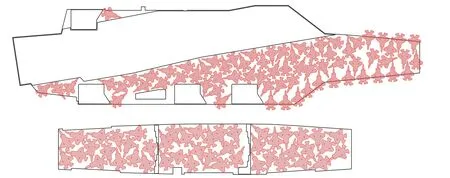
图14 F-35C飞机在飞行甲板和机库的最大布列图Fig.14 Maximum spotting pattern of the F-35C aircraft on the flight and hangar deck

6 结 语

本文以最低重心NFP算法为基础，针对舰载机最大密度布列的距离和超边界约束进行分析，提出了距离约束的数学模型及处理策略，以及利用启发式靠边定位算法来处理超边界约束，并基于飞行甲板和机库舰载机布列具体约束，分别提出了飞行甲板和机库最大密度布列的算法。利用该算法得到“尼米兹”航母可最大密度布列129架F/A-18C或115架F-35C飞机，以及F-35C飞机布列因子为1.12等有意义的结论，与美军相关文献公布的舰载机布列数据基本吻合，证明了算法的实用性。