密集障碍物下无人艇模糊双窗口DWA避障算法

张金泽，赵红，王宁，郭晨

1 大连海事大学 船舶电气工程学院，辽宁 大连 116026

2 大连海事大学 轮机工程学院，辽宁 大连 116026

3 哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨，150001

0 引 言

无人艇（unmanned surface vehicle，USV）是一种轻型智能水面运载工具，具有体积小、造价低、速度快、机动性强等特点[1]，在我国环境检测、科研勘探、水下测绘、搜索救援、安全巡逻等领域均有应用。

自主导航是USV的核心技术之一。在实际海洋环境中，特别是渔船作业区、港口、临海、锚地等复杂环境下，仅通过卫星拍摄的海图，很难实时获得环境的完整信息。例如，无人艇在大型水产养殖区执行饵料投放、水质检测等任务时，当水面上有临时停靠的渔船等障碍物时，就需要无人艇通过船载的双目视觉、激光雷达等传感器实时感知周围环境，获取局部的障碍物信息，进而应用局部路径规划方法使无人艇完成自主避障。经过国内外学者多年的研究，目前已经有很多成熟的算法用于无人艇的路径规划问题。局部路径规划常用的算法有人工势场法、向量场直方图（vector field histogram，VFH）法和动态窗口法（dynamic window approach，DWA）等。

人工势场法由Khatib[2]提出，其基本思想是建立虚拟的人工力场。障碍物会对无人艇产生斥力，目标点则对无人艇产生引力，引力和斥力的合力就会驱动无人艇运动。人工势场法具有数学描述简洁、计算量小、反应速度快、实时性高、规划轨迹平滑的优点，便于底层的实时控制[3]。但同时也存在一些固有的缺陷，比如存在局部极值点障碍物附近目标不可达等问题。

基于人工势场法的思想，Borenstein等[4]提出了VFH法。该算法是一种未知环境下的局部避障算法，其通过测距传感器测得的信息建立向量场直方图，进行两级环境数据压缩，并考虑无人艇在前进运动过程中产生的代价，进而得到最优的可行方向，具有实时性高、避障可靠等优点[5]。但是该算法没有考虑无人艇自身的运动学性能，导致无人艇在实际环境中并不能按照规划好的路径航行[6]。

为此，Simmons[7]提出了曲率速度法（curvature velocity method，CVM），即将避障问题转化为约束和优化速度空间的问题，考虑了无人艇的速度和加速度的限制。随后，Fox等[8]提出了更为完善的动态窗口算法（dynamic window approach，DWA）。该算法充分考虑了无人艇的运动学性能和环境约束等因素，已在无人艇避障领域得到广泛应用。

DWA算法是首先根据无人艇自身的运动学性能建立一个预选速度窗口，然后再通过评价函数优化得到最优速度（包括前进速度和艏摇角速度），其中评价函数综合考虑了艏向角、航速和安全性这3个因素。采用该算法能够直接获得无人艇的最优前进速度和艏摇角速度，规划的航行轨迹平滑，适合无人艇实际航行过程的特点。但原始DWA算法存在2个主要的问题：一是会导致无人艇选择从密集障碍物群的外围绕行，而无法从密集障碍物之间穿过，致使无人艇的航行路径过长；二是算法的评价函数权值固定，无人艇无法适应航行于密集障碍物海域时的复杂海况。为解决上述问题，有学者提出了改进的优化方法，如程传奇等[9]将全局路径规划和局部路径规划联系在一起，将A*算法与DWA算法融合后提出了一种全局动态路径规划算法，在保证规划路径全局最优性的基础上，可提高平滑性及路径规划的局部避障能力。Tang等[10]根据DWA算法提出了一种OAABHW（obstacle avoidance algorithm based on heading window）避障算法，该算法将窗口划分为艏向窗口和速度窗口，并构建了2个评价函数分别选择最优的避障速度和避障方向。Zhang等[11]引入强化学习算法，提出了一种基于强化学习的自适应避障算法，该算法采用自适应学习模块处理海风和涌流的影响，提高了无人艇的避障性能。田永永等[12-13]针对稠密障碍物场景和动态障碍物的运动特性，提出了自适应动态窗口法和基于速度方向判定的动态窗口法，在原始算法的基础上实现了改进优化。

上述改进措施虽然可以解决原始DWA算法存在的问题，但这些算法有的是基于DWA算法与其他算法相融合，增加了算法的复杂度，有的没有考虑无人艇实际船载传感器获取信息的范围限制，且没有规定对单个障碍物结束避障的边界，无法有效优化速度集合。鉴于此，本文拟提出一种双窗口DWA避障算法，即在常规速度窗口的基础上再设计一个基于艇载传感器的感知窗口，以对感知范围内的障碍物进行处理，并将感知窗口作为结束当前单个障碍物避障的边界，障碍物离开感知窗口即结束对其的避障。然后，在此基础上提出基于模糊控制策略的改进型双窗口（fuzzy-based dynamic double-window approach，FDDWA）算法，即利用所设计的障碍物密集程度函数来表征障碍物的分布情况，根据不同的实时海况信息，利用模糊控制策略动态调整评价函数中的权值参数，以使算法规划的路径更加安全、合理，提高无人艇的整体运行性。

1 原始DWA算法

1.1 原始DWA算法介绍

DWA的基本思想是：计算在每一个采样时间间隔内无人艇的可达速度，构成一个速度空间的集合，即动态速度窗口，然后通过构建的评价函数优化动态窗口，并从动态窗口中选择出最优的无人艇可行速度。

由无人艇运动学分析可知，其前进速度u和艏摇角速度r均存在上限值，分别将其设为umax和rmax，则无人艇的速度集合Vs(u，r)可以设置为：

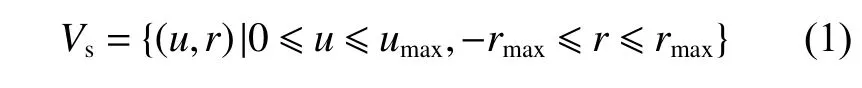
而对于一个给定的无人艇推进电机而言，其有限的输出力矩限制了无人艇在一个采样时间间隔dt内可以达到的最大速度和最小速度，故根据当前采样时刻的前进速度ucurr和 艏摇角速度rcurr，由式（2）可以得到下一个采样时刻无人艇的实际可达速度集合Vd(u，r)为：

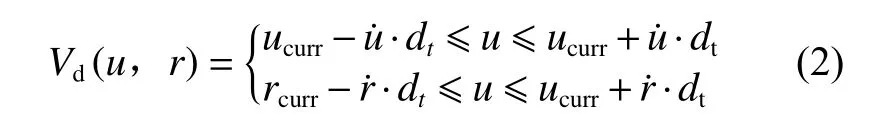
式中：u˙为 前进加速度；r˙为艏摇角加速度。

通过式（2），即可确定无人艇在下一个采样时刻可选速度的集合范围。但集合中的元素是连续的，为此，将集合中的速度离散化，即将集合根据前进速度离散间隔du和 艏摇角速度离散间隔dr离散为M个前进速度u和N个艏摇角速度r，离散后的每一个ui和ri组 成一个速度矢量(ui，ri)，则总共有M·N个速度矢量。

为保证无人艇在未知海域航行时能安全、有效地避开障碍物，需考虑制动距离的约束，即下一采样时刻的速度需满足无人艇与障碍物的距离小于制动距离SD。制动距离SD和考虑制动距离的可达速度集合VSD(u，r)的计算如式（3）和式（4）所示，其中，假定经过m个采样时段可令无人艇的前进速度降至0。

式中，D(u，r)为当前无人艇距离最近障碍物的距离。则动态速度窗口Vr(u，r)为Vs(u，r)，Vd(u，r)和VSD(u，r)的交集：

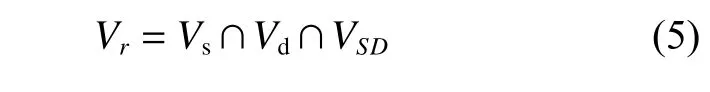
无人艇的全部轨迹是由n个 时段的n个小轨迹所组成，其每个采样时间间隔的运动轨迹方程如下：

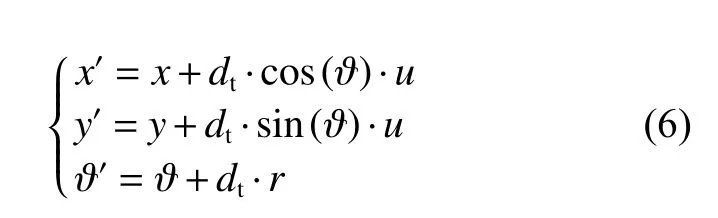
式中：x，y为无人艇当前采样 时 刻的坐标；x′，y′为无人艇位置信息更新后的坐标；ϑ为当前采样时刻无人艇的艏向；ϑ′为下一采样时刻无人艇的艏向。

将离散化后的全部速度矢量代入式（6），即可计算出T个采样时间间隔内的全部预测轨迹。无人艇在一个动态窗口内的部分预测轨迹如图1所示。

图1 无人艇部分预测轨迹Fig.1 Partially predicted trajectory of USV

构建一个兼顾无人艇航速、艏向以及安全性的评价函数G(u，r)，如式（7）所示，从动态速度窗口的Vr中 选择使评价函数G(u，r)值为最大的速度矢量 (u，r)，视为最优速度。

式中：H(u，r)用于评价无人艇的艏向，无人艇艏向完全指向目标区域位置时有最大值；S(u，r)用于评价无人艇的安全性，即预测轨迹中无人艇与障碍物间的最小距离，这个距离越大，发生碰撞的危险就越小；v(u，r)用于评价无人艇的速度，结果尽量选择动态速度窗口Vr中前进速度大的值；α，β，γ为对应的3个权值参数。而且，评价函数中H(u，r)，S(u，r)，v(u，r)的值都被归一化处理到[0，1]之间，以避免任何一项值过大。

对障碍物进行圆形包围体建模。对于船类障碍物，选择圆形包围体建模可以提高安全性，简化计算量，缩短计算时长，有利于算法的实时性和反应速度。外包圆具体的取值方法为：当传感器探测到障碍物位置时，以其探测位置作为原点，其直径取1.5倍的本艇长度，即R=1.5L。

1.2 基于原始DWA算法避障时存在的问题

在密集障碍物海况下，无人艇基于原始DWA算法进行避障时，主要存在2个方面的问题：

1） 原始DWA算法会导致无人艇选择从密集障碍物群的外围绕行，而无法从密集障碍物之间穿过，致使无人艇航行路径过长。

2） 无人艇在任务海域航行时其整体避障性能无法做到最优。无人艇为保证艏向和前进速度，通常会出现选择过激速度的情况，令无人艇与障碍物靠得非常近，从而威胁无人艇的安全。

将 α，γ参数固定，仅调节安全性权值参数β的对比仿真实验结果如图2所示，并将整个航行的轨迹长度、运行时间、安全距离（无人艇距离障碍物的最短距离）等具体实验数据列于表1中。当β=1时，由图2（a）及表1中的数据可见，无人艇在航行过程中若距离障碍物较近，容易造成无人艇与障碍物发生碰撞；但当β=15时，虽然安全性得到了提高，但航行轨迹长度增加了，运行时间增加了12.86%，算法的计算效率明显下降。

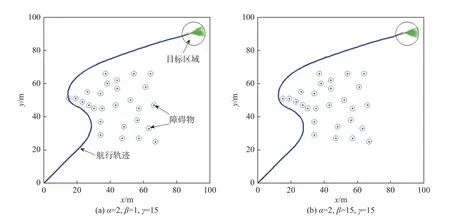
图2 基于原始DWA算法的无人艇航行避障轨迹Fig.2 Obstacle avoidance trajectory of USV based on original DWA algorithm

表1 实验结果数据Table1 Experimental result data

2 基于模糊控制策略的改进型动态双窗口算法

针对原始DWA算法存在的2个主要问题，本文提出了基于模糊控制策略的改进型动态双窗口（FDDWA）算法：

1） 提出了双窗口概念，即在原始动态速度窗口的基础上又设计一个扇形动态感知窗口，也即速度与感知双窗口，通过对感知窗口内障碍物的局部分布状态进行分析与处理，不仅可以有效提高算法的速度优化效率，而且还规定了局部障碍物结束避障的边界，可以避免无人艇过度绕行障碍物的问题，使避障轨迹更加平滑、合理。同时，通过设置最小安全距离Dmin，可避免算法选择过激速度。

2） 将模糊控制策略应用于双窗口DWA算法。根据复杂海况的不同障碍物信息，基于模糊控制策略动态调整评价函数中的安全性权值参数β和速度权值参数γ，可令无人艇在避障航行时兼顾安全性与航行速度，从而提高算法的整体运行性能。

2.1 感知窗口

实际应用中的无人艇可通过艇载的双目视觉、激光雷达来获取无人艇及障碍物的位置、距离等信息，通过这些传感器共同工作获得障碍物的完整信息。这些传感器通常只能探测一定范围内的信息，而原始DWA算法并未考虑传感器的这种局限性，为此，本文设计了一个如图3所示的扇形区域，即动态感知窗口来表示船载传感器的探测范围，不仅使算法更加适用于实际应用场景，而且还提高了算法优化效率。由于同时还规定了对单个静态障碍物结束避障的边界，因此当障碍物离开感知窗口时，即会停止对其避障，这样可避免过度避障行为，使避障轨迹更加合理。

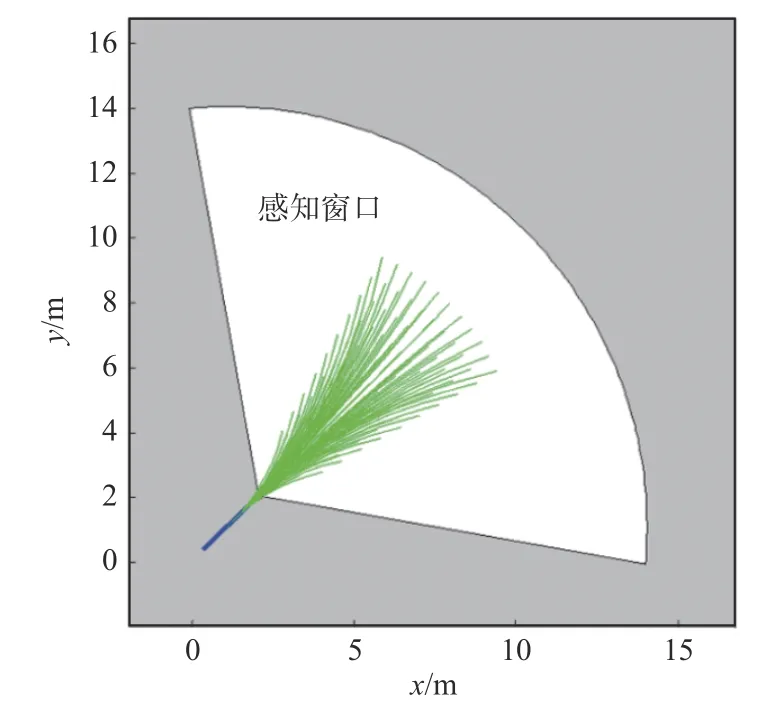
图3 感知窗口示意图Fig.3 Schematic diagram of sensing window

图4所示为无人艇分别基于原始DWA与本文改进型双窗口DWA算法所进行的航行避障对比仿真实验。由图可见，在固定权值参数α，β，γ的情况下，相比原始DWA算法，改进型双窗口DWA算法令无人艇在密集障碍物分布的复杂海域内航行时具有更加安全、合理的航行轨迹，航行轨迹长度缩短了24.62%，总运行时间减少了18.18%，算法的整体运行性能得到了显著提高。

图4 基于原始DWA与本文双窗口DWA算法的对比仿真实验Fig.4 Comparison experiment based on original DWA and improved dual-window DWA algorithm

2.2 设置最小安全距离

在密集障碍物分布的海域内航行时，无人艇的安全是根本，在任何情况下都不允许出现过激速度情况。为此，本文提出设置最小安全距离Dmin，以对速度集合进行进一步的筛选，将无人艇与障碍物之间距离小于Dmin的速度组合舍弃，确定新的速度窗口集合Vr′，如式(8) 和式(9)所示。

式中，VDmin为考虑最小安全距离的速度集合。

2.3 改进型模糊自适应双窗口FDDWA算法

2.3.1 密集度计算方法

船载传感器可以获取无人艇感知窗口内局部障碍物的完整信息，当采用模糊控制进行算法参数动态调整时，需根据任务海域内进入感知窗口的障碍物实时分布情况进行决策，因此，本文设计了一个表征障碍物密集度的函数I(n，d，s)，其定义如式（10）所示：

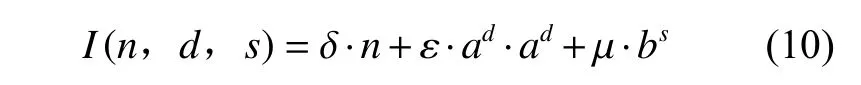
式中：n为障碍物个数；d为感知窗口内距离无人艇最近的2个障碍物之间的距离；s为在感知窗口内探测到的由所有障碍物组成的多边形的面积；δ，ε，µ为 各个部分的权重系数；a，b为指数函数的底数系数。密集度函数I(n，d，s)的值越大，表示感知窗口内障碍物的分布情况越密集，图5所示为针对不同障碍物分布情况的仿真分析结果。

当视觉窗口中障碍物的分布如图5（a）所示时，密集度函数的值为0.615 7；当视觉窗口中障碍物的分布如图5（b）所以时，密集度函数的值为1.960 0；当视觉窗口中障碍物的分布如图5（c）时，密集度函数的值为2.560 0。实验结果表明，本文所提的密集度函数可以有效地表示感知窗口内障碍物的密集程度。

图5 密集度示意图Fig.5 Schematic diagram of density

2.3.2 模糊自适应双窗口FDDWA算法

模糊控制是以模糊集理论、模糊语言变量和模糊逻辑推理为基础，将人的经验应用于控制规则的智能控制方法，具有鲁棒性好、可以增强控制系统自适应能力的优点。为解决前述原始DWA算法固定权值参数所引发的问题，本文提出了一种基于模糊控制策略的FDDWA算法，可根据无人艇在航行中的实时海况自适应动态调整权值参数β 和γ，令其在复杂海域内的航行路径转折更小，同时兼顾速度和安全性因素，采用该算法后，其整体运行性能更高。

设计的模糊控制器采用的是双入双出结构，输入变量为密集度函数值I及无人艇与最近障碍物间的距离D，输出变量为权值参数γ 与β，各输入、输出子集如表2所示，对应的论域及隶属度函数如图6所示，模糊控制规则如表3和表4所示。

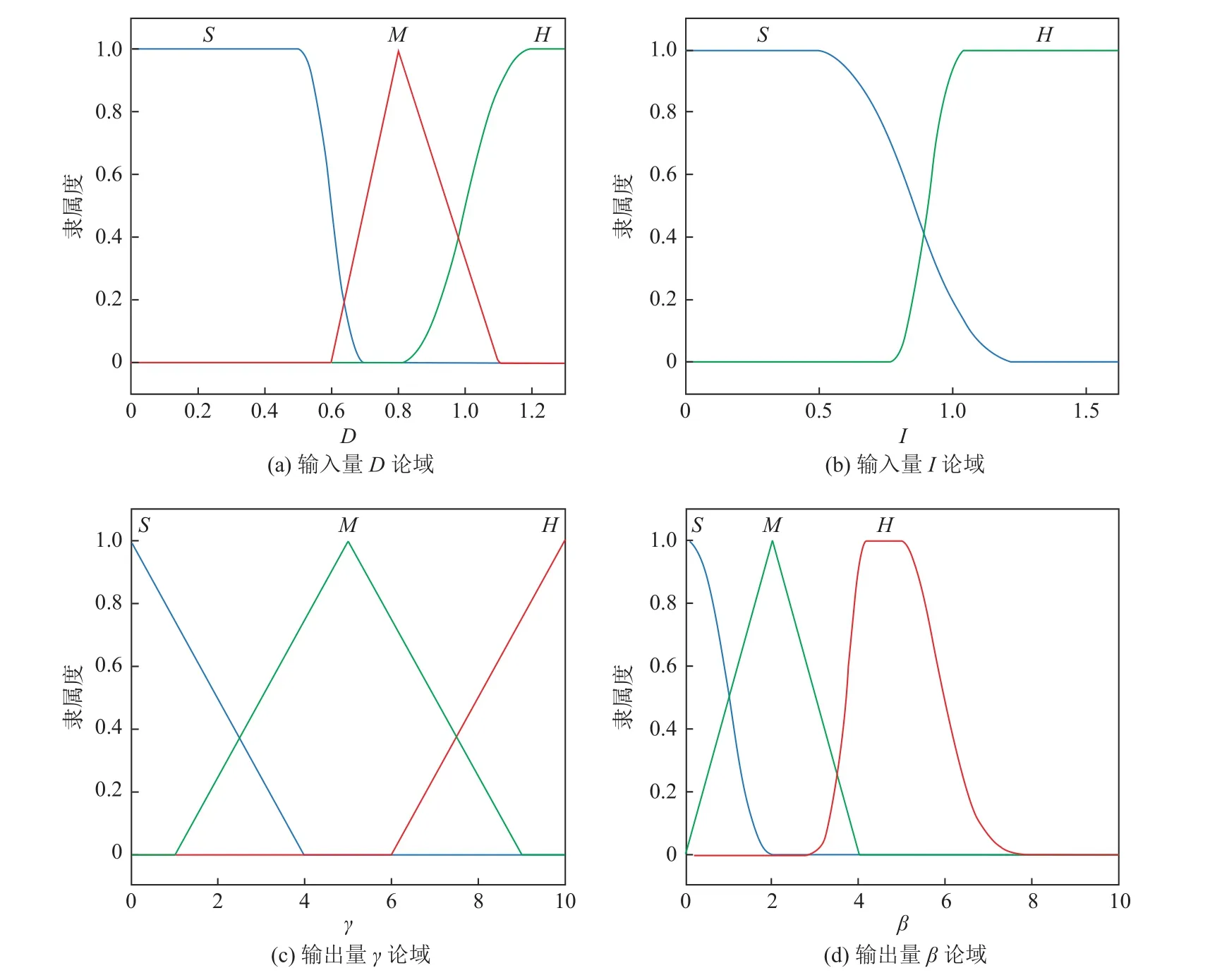
图6 模糊逻辑变量的隶属度函数Fig.6 Membership function of fuzzy logic variables

表2 模糊逻辑控制输入输出子集Table2 Fuzzy logic control input and output subset

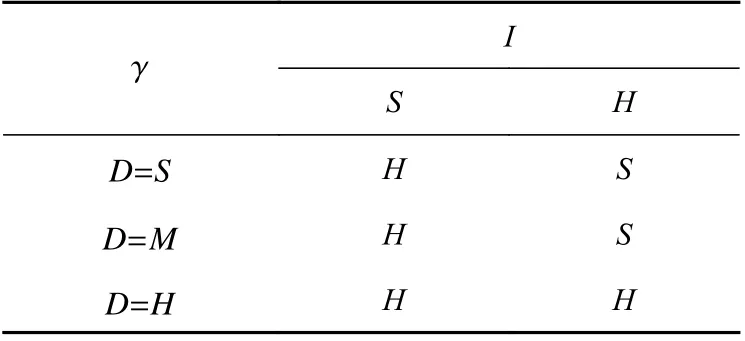
表3 输出量γ的模糊规则Table3 Fuzzy rules of γ

表4 输出量β的模糊规则Table4 Fuzzy rules of β

2.4 FDDWA算法流程

FDDWA算法的流程步骤如下：

1） 确定无人艇的起点和目标范围，计算动态速度窗口；

2） 更新动态速度窗口，计算预测轨迹；

3） 通过艇载传感器更新动态感知窗口内障碍物信息，计算I和D；

4） 由模糊控制器根据当前的I和D计算γ和β，代入评价函数；

5） 根据评价函数选择最优速度；

6） 执行速度，更新位置，判断是否到达目标区域，若是，则结束，否则，返回步骤1），进入下一循环。

3 无人艇避障仿真实验

为了验证本文所提FDDWA算法的有效性与优越性，在一片障碍物密集分布的任务海域内，对无人艇基于固定权值参数的双窗口DWA算法和FDDWA算法进行了对比仿真实验。有关无人艇和算法的一些参数如表5～表8所示。

表5 无人艇速度限制Table5 Speed limit of USV

表6 算法参数设置Table6 Parameter settings of algorithm

表7 密集度函数参数设置Table7 Parameter setting of density function

表8 无人艇及感知窗口初始状态设置Table8 Initial state setting of USV and sensing window

3.1 基于固定权值参数双窗口DWA算法的无人艇避障仿真实验

1） 权值参数选取 α =2，β=1，γ=15。

由图7所示的仿真实验结果可见，无人艇的航行轨迹相对平滑，没有出现较大的转弯现象，但通过密集障碍物区域时安全性较低，安全距离仅3.34 m。无人艇在整个航行过程中基本保持全速航行，受障碍物影响的航速波动及艏摇角速度波动均较小。因此，若需强调无人艇的航行速度，可将β设置得较小，γ设置得较大，但这样安全性会较差。

图7 双窗口DWA算法下α =2，β=1，γ=15 时的仿真实验结果Fig.7 Simulation experiment results when α =2，β=1，γ=15 under the dual-window DWA algorithm

2） 权重参数选取 α =2，β=15，γ=15。

由图8所示的仿真实验结果可见，与图7的结果相比，无人艇通过密集障碍物区域的安全性得到了改善（安全距离增至3.56 m），但航行轨迹转弯较多，无人艇在整个航行过程中难以保证全速前进，且受障碍物影响的航速波动及艏摇角速度波动均较大，需频繁转向变速。因此，若需强调无人艇航行的安全性，可将β设置得较大，γ设置得较小，但这样避障路径不尽合理，且运行时间会变长。

图8 双窗口DWA算法下α =2，β=15，γ=15时的仿真实验结果Fig.8 Simulation experiment results when α =2，β=15，γ=15 under the dual-window DWA algorithm

3.2 基于FDDWA算法的无人艇避障仿真实验

基于FDDWA算法的无人艇避障仿真实验结果如图9和图10所示，其中的实时动态权值参数用 βd，γd表示。与图7和图8相比，基于FDDWA算法的无人艇的航行路径更加平滑、合理，无人艇通过密集障碍物区域时的安全性更高（安全距离增加至4.09 m），且在整个航行过程中几乎是保持全速航行，受障碍物影响的航速波动及艏摇角速度波动均较小，一些相关的算法运行数据如表9所示。

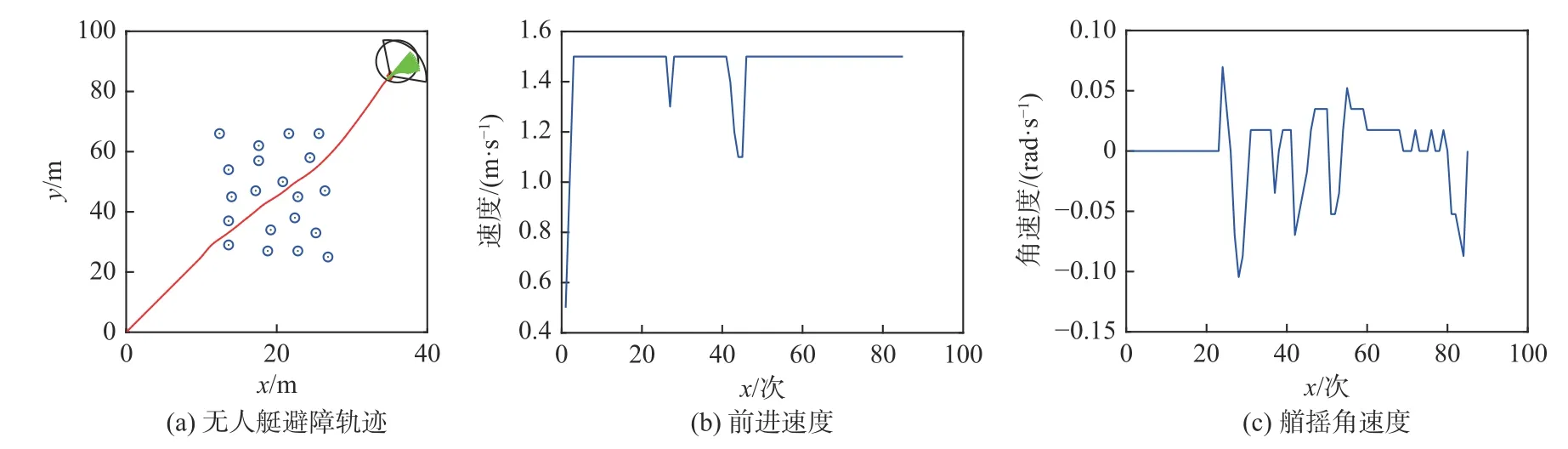
图9 基于FDDWA算法的无人艇避障仿真实验结果 (α =2，β=βd，γ=γd)Fig.9 Simulation experiment results of obstacle avoidance for USV based on FDDWA algorithm (α =2，β=βd，γ=γd)

图10 不同权值参数下的无人艇避障轨迹对比Fig.10 Comparison of USV's obstacle avoidance trajectory under different weight parameters

由表9中的数据可知，相比固定权值参数设置（ α=2，β=15，γ=1）的双窗口算法，采用动态参数的FDDWA避障算法的迭代次数降低了28.24%，运行时间降低了43.43%，轨迹长度降低了2.58%，算法效率明显得到提高；而相比α=2，β=1，γ=15的参数设置，FDDWA的迭代次数、运行时间和轨迹长度基本不变，但安全距离提高了22.46%，安全性得到显著提高。仿真结果充分验证了本文所提FDDWA算法的有效性与优越性。

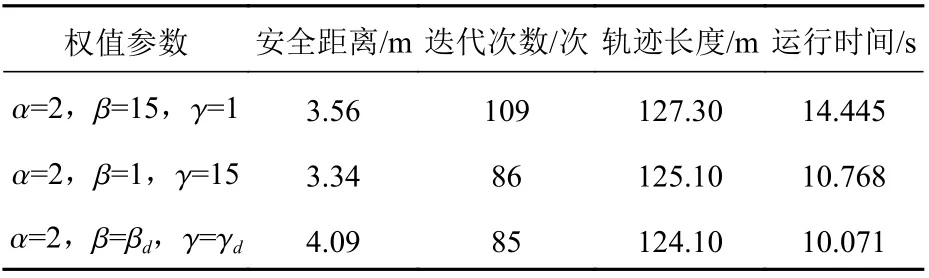
表9 实验数据Table9 Experimental data

4 结 语

本文首先针对原始DWA算法未考虑各传感器探测范围的限制，也未规定对单个障碍物结束避障边界的问题，设计了一个扇形动态感知窗口，然后与速度窗口一起构成速度与感知双窗口模型，用于对感知窗口内的障碍物分布情况进行分析与处理，待单个障碍物离开感知窗口即结束对其的避障。同时，通过设置最小安全距离Dmin，避免了算法选择过激速度。然后，针对算法评价函数权值固定、无人艇在任务海域航行时的整体避障性能无法做到最优的问题，提出了基于模糊控制策略的FDDWA算法，通过动态调整评价函数中的参数β 和γ来适应变化的环境，用以优化算法的避障性能。仿真实验结果证明，本文提出的FDDWA算法不仅可以避免无人艇过度绕行密集障碍物群的问题，还可以大幅改进算法的运行效率和避障性能，使避障轨迹更加合理、安全，对无人艇自主避障技术研究有一定的参考价值。