强化学习模式下舰船多状态退化系统的维修策略

程俭达，刘炎*，李天匀，初云涛

1 华中科技大学 船舶与海洋工程学院，湖北 武汉 430074

2 中国舰船研究设计中心，湖北 武汉 430064

0 引 言

在舰船这样的大型结构中，存在着大量的退化系统，例如船体结构、武器装置以及动力设备等。船舶在服役过程中受到的损耗、疲劳、腐蚀等将导致系统的故障率上升，进而影响舰船及设备的安全运行[1]。舰船的装备维修是保证可靠性及战备完好性的重要手段[2]，现有的维修方式以预防性的定期维修为主，装备的维修时机与其服役时间直接相关。然而，定期维修可能存在维修不足或维修过剩、维修难度逐渐增加，以及无法预防与时间无关的故障等问题[3]，进而导致全寿命周期的维修成本有所增加。随着舰船装备逐渐向基于状态的视情维修发展[4]，亟需智能化的维修决策工具，因此，有必要开发船舶智能诊断系统[5]。

视情维修的基本思想是：通过正确、可靠地预测系统当前和将来的运行状态，从而安排维修活动[6]，故视情维修可以有效解决定时维修导致的维修不足或维修过剩等问题。马尔科夫决策过程（Markov decision process，MDP）是解决退化系统最优视情维修决策这一问题的有效工具，在MDP中，状态、行为及奖励分别对应了退化系统的退化状态、维修措施及维修成本。Moustafa等[7]利用马尔科夫链建立了一个多状态的退化系统模型，在每个状态采取了3种维修模式，并通过最小化预期成本求解了最优维修策略。程志君等[8]基于马尔科夫决策过程，通过位相型（phase-type，PH）分布来拟合状态转移概率，从而简化了马尔科夫决策过程的求解方法。Zheng等[9]利用Gamma过程以及PH分布来拟合系统失效过程，增加了更多的维修措施，并在状态设置中增加了除退化程度之外的时间值，从而更加接近真实的退化过程。Kim等[10]建立了一个包含多种退化状态及2种软/硬失效状态的MDP模型。Wang等[11]采用马尔可夫决策过程以及策略迭代算法，分析了某发动机的最优维修方案。江晓俐[12]采用马尔可夫决策过程讨论了船舶结构退化问题的最优维修方案。

对于船舶的视情维修而言，维修决策需要最大限度地延长机件系统的工作时间并保持战备可用性，同时还需要开展针对性维修以充分利用资源，这对维修决策工具提出了极高的要求。目前，数据驱动方法在舰船工程领域展现了极具前景的问题解决能力[13-14]，即利用强化学习方法训练出船舶维修决策系统的辅助决策方法。在求解MDP的强化学习方法中，Q学习算法作为不依靠模型的经典算法，无需预先已知模型动态，仅需知道其状态、行为以及奖励即可；同时，Q学习算法结合了策略迭代和值迭代的优点，即每次迭代后均利用当前估计值来近似目标值，无需等到迭代结束再进行更新。郭一明[15]将模拟退火算法与Q学习算法相结合，用于解决MDP优化结果中的局部最优解问题。Wei等[16]利用深度Q网络模型计算了大量状态的MDP问题，并将其应用到某桥梁退化模型中得出了其最优维修策略。强化学习结合船舶退化结构维修策略的学习过程包括代理（船舶维修决策系统）、环境（船舶退化状态）、维护动作及动作成本等，其目标在于训练船舶的维修决策系统如何在与环境交互过程中学会最大化累计收益的维修行为，需注意的是，强化学习的目标应用领域包含了退化系统的维修决策分析。

为此，本文拟提出强化学习模式下舰船多状态退化系统维修策略的求解方法。首先，将介绍马尔科夫决策过程对系统退化及维修的建模方法；然后，分析强化学习中Q学习算法的实现过程，其中经Q学习算法优化的Q值表将用于代理辅助视情维修决策；最后，将采用文献[12]中舰船结构多状态退化模型来验证本文所提出方法的可行性和响应速度，用以为决策者提供视情维修的智能化辅助决策工具。

1 基于MDP的退化模型

MDP为求解强化学习问题提供了一个数学框架。根据马尔科夫特性，未来状态仅取决于当前而与过去状态无关，因此，马尔科夫链是一个概率模型，仅依赖当前状态来预测下一个状态。MDP是马尔科夫链的一种扩展，一般由5个关键要素构成：

1） 系统所有可能存在的状态空间集S。

2） 系统从一种状态转移到另一种状态所执行的行为集A。

3） 系统执行某一行为a之后，从状态s转移到状态s'的概率。

4） 系统执行某一行为a之后，从状态s转移到状态s'的奖励R，即维修行为对应成本的负值。

5） 折扣因数γ。

在基于MDP的退化系统模型中，假设退化系统的状态空间集S由N+1个状态构成，令S= {sn|n= 0, 1, 2, ···,N}，其中：n= 0表示该系统处于初始状态，没有发生任何退化现象；n= 1, 2, ···,N−1表示不同退化程度的中间状态，下标数值越大，则退化程度越高；n=N表示该系统处于失效状态。假设退化系统的行为集由M个不同的维护措施构成，令A= {am|m= 1, 2, ···,M}。在不同状态下，如果采取不同的维护措施，则船舶结构将发生不同的变化，当退化结构进行第i次（i≥1）维修决策时，此时状态记为si（si∈S）时，如果采取维修行为ai（ai∈A），则该结构进入状态si+1（si+1∈S）的概率为Pi,i+1|ai，同时该维修行为ai的投入成本为ci。在每次维护之前，需对结构状态进行检测，其检测成本为cin。此外，系统在每个状态存在相应的运行成本，运行成本为单位运行成本e与运行时间t的乘积；在开展维修时则会产生停机成本，停机成本为单位停机成本b与本次维修时间ri的乘积；系统进入失效状态时，也会产生失效成本cf。将每次执行维修行为ai之后产生成本ci的负数记为奖励Ri，则

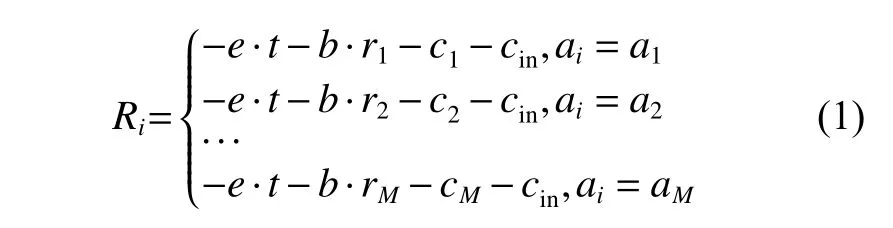
式中，r1,r2, ···,rM和c1,c2, ···,cM分别为维修行为a1,a2, ···,aM的维修时间和投入成本，。

将概率Pi,i+1|ai记为一个矩阵，则每种维修行为都对应一个转移矩阵，将行为a的状态转移矩阵记为Pa。图1展示了整个基于MDP的退化状态转移过程，其中同一个状态执行维修行为之后的状态是不同的，存在随机性。需注意的是，基于MDP的退化系统模型存在如下假设：

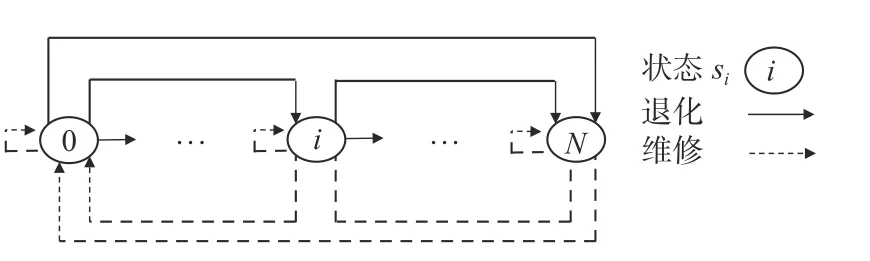
图1 马尔科夫过程的状态转移Fig.1 State transition of Markov process

1）系统退化过程中的各个状态（初始状态到失效状态）对应了系统的某些特征参数（例如，疲劳裂纹长度和腐蚀层厚度），可以将该系统划分为多个不同的退化状态。当系统的特征参数在某一状态的数值范围内时，即可判定系统处于该状态。

2）系统进入每个状态之后，通过检测即可准确获知该系统的状态信息，且不考虑检测成本所带来的影响。

本文将基于马尔科夫决策过程建立多状态的退化系统模型，当退化系统处于状态si时，即可根据最优维修策略采取行为am，从而使系统在全寿命周期的总成本最低。通过引入强化学习算法对维修成本和收益进行综合权衡，即可求解最优的视情维修策略。

2 强化学习

本文中强化学习的主要目的是训练代理（船舶维修决策系统）在与环境交互过程中学习最大化累计奖励的行为，其过程如图2所示。

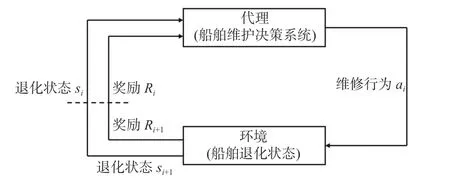
图2 强化学习过程Fig.2 Reinforcement learning task

强化学习中的Q学习算法是一种应用广泛的时间差分算法[17]，该算法着重考虑的是状态-行为值Q(s,a)，即在状态s下执行行为a之后的累计奖励，最终所有的状态-行为组合将形成Q值表。通过比较同一状态下不同行为的Q值，选取奖励最高的行为作为该状态的最优行为，然后集合所有状态下的最优行为，即可生成最优策略。

船舶的退化过程是半马尔科夫过程，即在没有维修行为时退化转移过程只会向更坏的状态转移，而Q学习算法则可以通过学习和训练来制定不同状态下的维修行为策略，具体步骤如下：

1） 首先，初始化Q值表，通常设为0。由退化模型的状态空间集S和行为空间集A可知，初始化之后的Q值表是一个M列N+1行的表格，第n+1行的M个数值分别代表了sn状态下M种维修行为的价值。

2） 选择一次新的情景（Episode），设定情景中进行维修决策的总次数为st，其中：

（1） 设定船舶的初始状态si(si∈S)，此时i= 1。

（2） 进行第i次维修决策，根据ε-贪婪策略（ ε ＞0，为贪婪概率），在状态si下执行某一维护动作ai，并转移到新的状态si+1，产生的相应成本（包含维修成本，运行成本以及停机成本），根据式（1）即可计算维修行为奖励Ri，即该次成本的负值。

（3） 根据式（2）的更新规则，对状态-行为值Q(si,ai)进 行更新，得到Qnew(si,ai)；然后执行第i+1次维修决策。

（4） 重复执行步骤（1）～步骤（3）st次。利用蒙特卡洛方法和式（3）计算当前情景策略下的全寿命周期总成本C，同时根据式（4）计算前后2次情景更新后Q值的相对变化δQ。

3） 重复执行步骤2），通过多次情景迭代并更新Q值，直到Q值变化减小且满足停止标准δstop时 ， 将δQ连 续小于 δstop的 次数记为nδ，即可停止循环得到最终的Q值表。

4） 根据Q值表，选择在所有船舶状态sn下Q值最大的维修行为am，即可生成最优维修策略。

式中：0＜α＜1，为学习率，也称为步长，主要用于迭代收敛；0＜γ＜1，为折扣因数，表征了未来奖励和即时奖励的权重；nQ为Q值的个数；Q′(s,a)和Q(s,a)分别为完成前后2次情景更新之后的Q值。

松弛通常是面团在整形操作后，筋力收紧，如果再进行操作的话，面团收缩变形，不利于整形，因此松弛一定的时间，再进行下一步的操作，时间为5～10 min。中间醒发是相对最后醒发而言的，中间醒发也可以理解是长时间的松弛或者是中种面团的醒发，因为在有些面包品种中，虽然是一次搅拌，可能由于时间的原因经过多次发酵，因此就不好确定哪次的醒发属于中间醒发。最后醒发是烘烤前的最后一步，经过最后醒发的面包即将进入烤箱烘烤。因此了解松弛、中间醒发、最后醒发的特点和目的，就可以调节这几个环节的时间、次数。

ε-贪婪策略即每次采取维修行为时，有ε的概率随机选择当前状态下能够选择的所有行为，而剩余1−ε的概率则应根据Q值表执行在当前状态下Q值最大的行为，即ε-贪婪策略保证了所有Q值的选择概率。Watkins[18]对Q学习算法的收敛性进行了证明，其结论是：只要在所有状态下重复执行所有的动作且所有状态-行为值Q(s,a)均为离散，则Q学习就会以1的概率收敛到最优。本文中的维修行为和状态对应的Q值均为离散值，因此符合收敛性要求。

图3展示了Q学习算法在一次情景下的实现步骤，首先基于{si,ai,si+1,Ri}对Q值表中的相应数值进行更新，然后应用ε-贪婪策略，其中Q学习算法的核心是Q值更新公式（式（2））。在该退化系统模型中，折扣因数γ的选择主要取决于即时奖励和未来奖励的权重，γ越接近于1即表示更重视未来奖励，而γ越接近于0则表示更重视即时奖励。由于退化系统是一个长时间持续性的系统，因此，应用Q学习算法时，宜设置较大的情景迭代次数进行模拟。

图3 在一次情景中Q学习算法的实现步骤Fig.3 The steps of Q-learning algorithm in one episode

3 船舶结构的维修决策算例

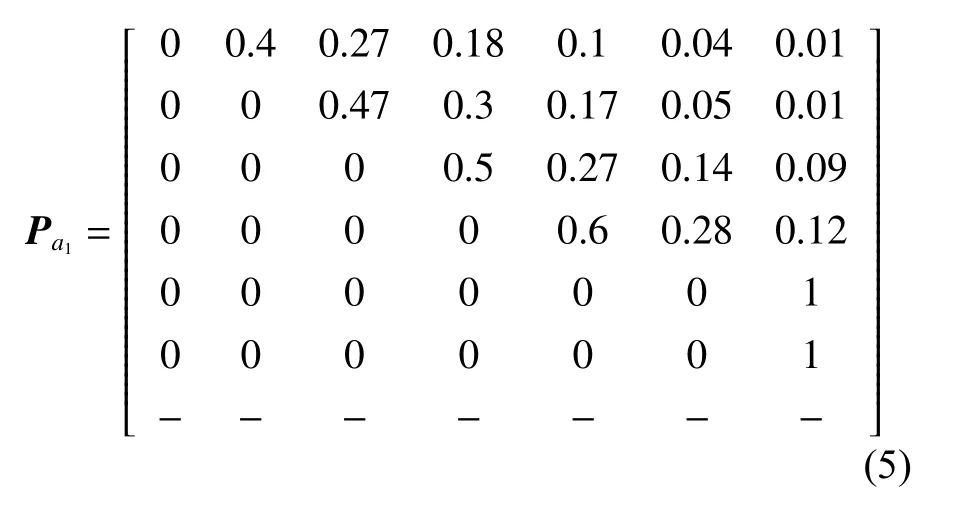
舰船系统装备的数量多、品种多，且工作环境较为恶劣，所以其故障发生率较高。本文的演示算例将引入文献[12]中某舰船结构的退化系统模型，并将该模型的维修措施由2种增加到3种，同时将考虑维修效果的不确定性。该舰船结构退化过程的状态空间为S= {s0,s1,s2,s3,s4,s5,s6}，分别对应了完好（s0） 、可见裂纹维修（s1）、油漆和阴极防护维修（s2）、腐蚀修理（s3）、疲劳裂纹修理（s4） 、腐蚀疲劳组合修理（s5）以及完全失效（s6）这7个状态。行为空间集A= {a1,a2,a3,a4}，分别表示不采取任何维修（a1） 、最小维修（a2）、中度维修（a3） 以及最佳维修（a4），且假设后3种维修措施的效果不到位，其维修成本和维修时间分别为c2，r2，c3，r3，c4，r4。在贪婪策略中，完好状态s0下仅能选择“不维修”，失效状态s6下仅能选择“最佳维修”，而其他状态下这4种行为均可供选择。根据不同的状态及不同维护措施的成本，计算其转移概率，式（5）～式（8）展示了4种行为的状态转移矩阵Pa1，Pa2，Pa3，Pa4，其中：第n+1行第n′+1列表示从状态sn转移到状态sn′的概率（n，n′=0, 1,2, ···, 6，为该系统算例的状态编号，且n≠n′）；符号“−”表示在此状态下不能采取该动作。

表1所示为不同退化状态下的成本和时间，本算例中采用的各成本数值与单位都来源于文献[12]并作了一定的假设，其中：单位停机成本b=100元；符号“−”表示在该状态下不适合执行维修行为。在失效状态下仅能选择最佳维修，其失效成本cf=15 000元，检测成本cin=200元。当系统状态越差时，越趋于老化状态，其失效概率和运行成本也越高，因此，本文算例中的单位运行成本将随着状态退化而逐渐增加。

表1 各状态下的维修成本Table1 The cost of different actions in different states

本文Q学习算法的参数设置为：折扣系数γ=0.85（假设通货膨胀率为5%，预期收益率为10%）；学习率α=0.001；每个情景的迭代次数为100次；贪婪概率ε=0.15，其值将随着迭代情景先增加而后减小；停止条件 δstop=1 .5×10−4；nδ=2 000。

表2所示为Q学习算法的迭代结果，在经过5 473次情景迭代之后，满足停止条件，最优维修策略为[a1,a2,a3,a4,a4,a4,a4] ，即状态s0采取不维修措施，状态s1采 取最小维修措施，状态s2采取中度维修措施，s3,s4,s5,s6均采取最佳维修措施。图4所示为情景迭代次数与维修策略全寿命周期总成本C之间的关系，从图中可以看出，随着迭代次数的增加，C将逐渐减少到43 000元左右。图5所示为Q值的变化情况：当情景更新3 000次之后，其变化率 δQ＜1.5×10−4；当循环迭代5 473次之后，满足停止条件，则停止迭代。根据C和δQ，即可确定最优维修策略。

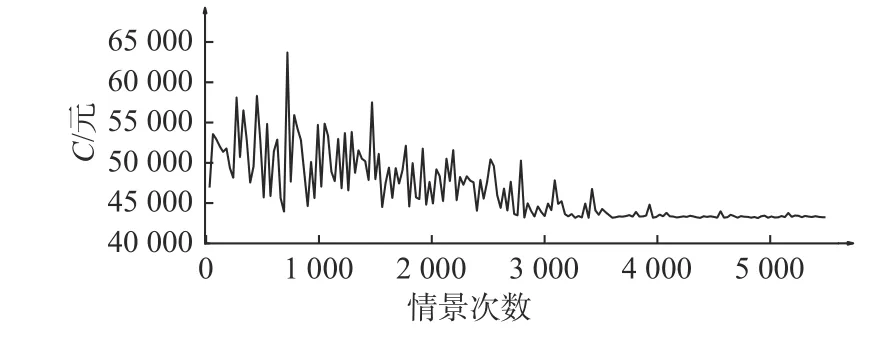
图4 全寿命周期总成本C随着迭代次数的变化曲线Fig.4 Variation of life-cycle cost C with respect to episode iterations

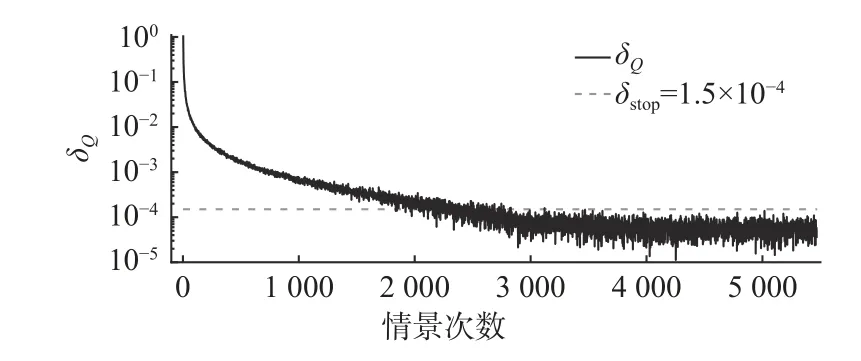
图5 收敛性条件随着迭代次数的变化Fig.5 Condition of convergence with respect to episode iteration

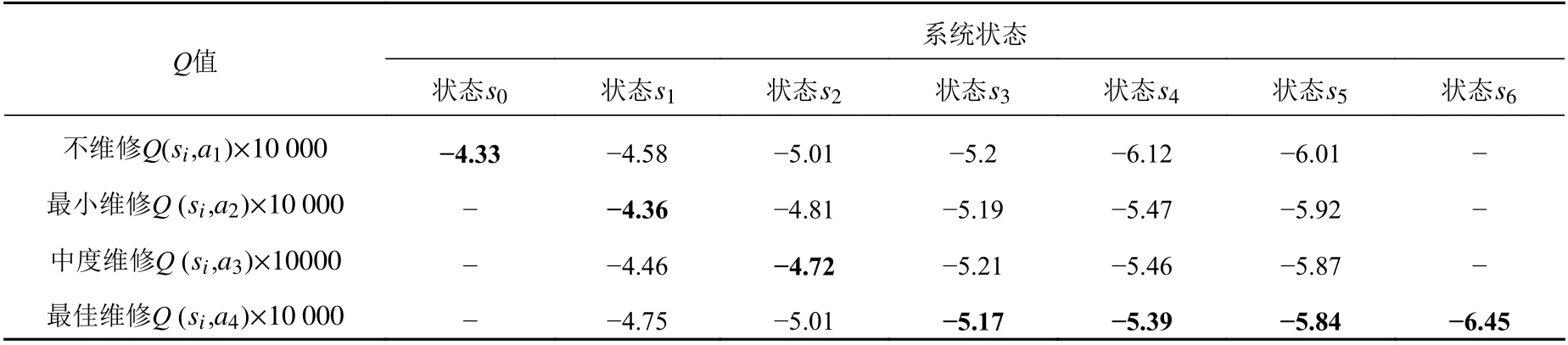
表2 Q值表Table2 The Q value table

表3所示为最优维修策略随折扣系数γ的变化情况，随着折扣系数γ的减小，维修行为所对应的Q值也随之减小，而最优维修策略也会相应改变。由此可见，γ越小，即代表所选择的维修策略越注重短期利益，即维护成本较低的不维修a1及最小维修a2；当折扣系数较大时，迭代过程更注重系统的长期成本，其最优维修措施将相对保守，即中度维修a3及最佳维修a4。对于决策者来说，当通货膨胀率或预期收益率较高时（折扣系数较小），可以选择成本较低的维修措施，从而获得最小成本或最大收益。

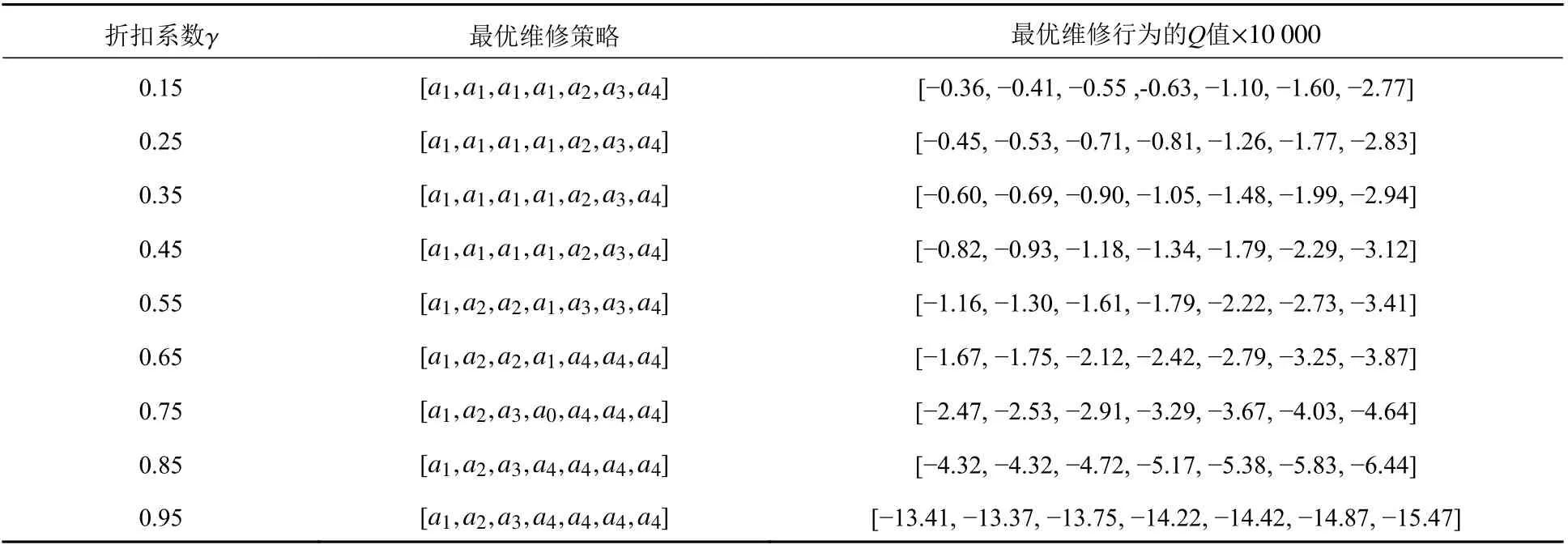
表3 不同折扣系数γ下的最优维修策略Table3 The optimal maintenance strategy with different γ values

表4所示为不同检测费用对维修策略和全寿命周期总成本的影响。从表中可以看出，随着检测成本的增加，全寿命周期总成本随之增加，而最优维修策略没有变化，产生这种结果的原因是视情维修是基于成本而进行维修决策。通过公式（1）可以看出，不同维修行为产生的奖励区别在于维修成本和停机成本，而检测成本的变化对于所有的维修行为的影响是相同的，因此检测成本的增加只会导致全寿命周期总成本的增加而不会改变最优维修策略。

表4 不同检测成本下的最优维修策略Table4 The optimal maintenance strategy with different cost of inspection

4 结 论

1） 舰船装备的维修决策需要对系统的安全、维修成本收益等进行综合权衡，基于强化学习方法求得Q值表为这一问题提供了很好的解决思路。系统维修决策不仅需考虑当前状态，还需考虑全寿命周期的运行成本，才能获得最大的累计收益。

2） 不同的折扣系数，即市场行情，对最优维修策略有一定的影响。检测成本对维修策略的影响较小，而对全寿命周期总成本的影响较大。

本文提出的方法适用于求解船体结构、武器装置、动力设备等系统，以及疲劳裂纹、腐蚀损伤、冲撞等退化系统的最优视情维修策略，为决策者提供了一个制定维修方案的智能化辅助决策工具。对于实船应用中退化系统的状态划分、退化过程的连续性与离散性等问题，将在后续工作中开展进一步研究。