滑坡下成品油管道力学响应研究

蒋宏业，兰旭彬 ，王金荣，胡海洋，王 涛

1.西南石油大学石油与天然气工程学院，四川 成都 610500

2.中国石油天然气管道工程有限公司，河北 廊坊 065000

3.中航油彭州管道运输有限公司，四川 成都 610500

引言

截至2019 年，中国油气管道实际总里程已达12.66×104km，已基本实现覆盖全国的管网布局。而管道在进行敷设时，不可避免的会穿越滑坡等地貌特征较危险的地带，在岩土体滑移影响下，致使管道受到挤压、剪切等载荷作用，使其裸露、悬空，甚至屈服、断裂。

针对滑坡下管道力学分析，众多学者也相继开展相关研究工作。其中，朱勇等[1]在全尺寸滑坡试验的基础上，基于Winkler 假设，将土体采用接地弹簧单元进行描述，忽略了土体变形的连续性。Han 等[2]利用ABAQUS 软件，针对滑坡体内/外分别采用PSI/土弹簧模型，对土体作用进行简化处理，其模拟结果精度取决于弹簧布设密度及其刚度选取。张伯军[3]考虑材料、接触、几何非线性，研究内压、径厚比等因素对管体位移影响，结果表明,管体极限偏移量随内压增大而减小。练章富等[4]利用ABAQUS 软件中的PSI 单元建立管道纵穿滑坡体的有限元模型，对不同斜坡角度和滑坡长度下的管道最大应力、应变变化进行分析。结果表明管道最大应力、应变随滑坡长度、斜坡角度的增大而增大。

已有研究通常将管内输送介质进行简化处理，即只考虑内压影响，而对于输油管道内存在的成品油，在滑坡作用下，势必会受到沿管壁传递的外载影响，在管-油交界面处产生相互作用；此外相比于输气管道，成品油自身重力的存在，也会对管道的受力情况带来一定程度的影响。

鉴于此本文以成品油管道为研究对象，建立基于SPH-FEM 算法的土-管-油完全耦合模型，进行力学响应研究，获取在管-油作用基础上的管体受力规律，并对多种主控因素对管道损伤行为带来的影响进行讨论，为获取滑坡灾害下管道更为精确的受力情况提供一种可行的模拟方法，进而确保其在外载作用下的可靠性。

1 作用模型及相关算法的选取

1.1 土-管-油相互作用模型选择

为进行滑坡下管道力学响应分析，重点在于管土相互作用的实现，现如今广为使用的管土作用模型有：弹性地基梁[5]、土弹簧[6-7]及非线性接触模型[8-10]。对于前两者，在建模时对土体进行简化处理，管土相互作用通常以弹簧形式进行传递，不能真实反映实际情况。且埋地管道受覆土作用而发生形变的同时，也会受到侧土的抗力作用，而在一定程度上减缓管道继续发生变形[3]。因此，在进行分析时，须把管周一定范围内的土体作为结构的一部分加以考虑，进行完全耦合建模，以更长的计算时间为代价，获取更高精度的模拟结果。

随着仿真软件的不断发展完善，非线性接触模型得到推广应用，其原理是在管土的交界面处通过定义接触面的形式实现运动方程等信息的传递，优势在于能够对管土之间的滑动与分离进行仿真模拟。由于篇幅受限，其模型详细介绍可参考已公开发表的文献[8-10]。而对于管-油相互作用，同样可采用此接触模型进行模拟计算。

1.2 SPH-FEM 耦合算法

有限单元法（FEM）作为传统网格法的一种，在对小变形相关问题的求解上，其准确性及效率方面具有更大的优势。

但为避免滑坡发生时，滑坡体及管内成品油因过大形变而致使网格发生畸变，迫使计算终止，而引入光滑粒子流体动力学法（SPH），将问题域离散为一系列不依赖于网格的粒子，从根本上解决网格法在处理大变形问题时所面临的难题。其算法本质是将粒子点上的值以积分插值形式计算得到密度、压力等宏观物理变量f（x），并利用粒子近似方法将其离散化，其相关计算如下式所示[11-12]

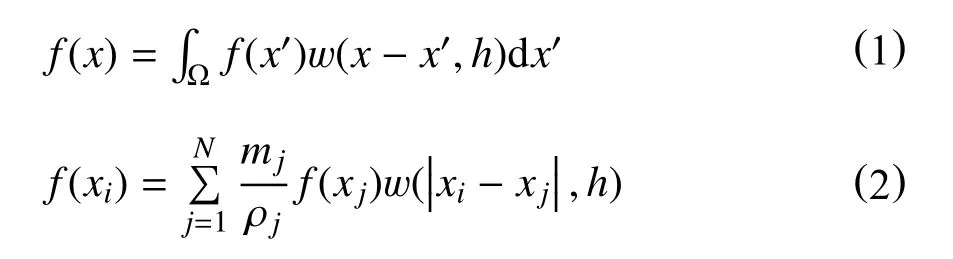
为避免SPH 法边界难处理、计算效率低等难题[13]，本文采用SPH-FEM 耦合的形式，充分发挥两者优势，即将滑坡体及成品油大变形区域SPH 粒子化，将小变形区域的滑坡床及为便于边界处理的管道FEM 网格化。并采用自动点对面接触形式实现粒子区与网格区应力、应变等信息的传递，进而实现SPH-FEM 耦合分析。同时为避免SPH 粒子与FEM 网格间接触穿透的发生，采用罚函数形式加以约束，即当在接触界面检测到穿透时，引入一个与穿透深度及接触刚度成正比的界面接触力，限制其穿透。

2 土管油耦合模型建立

2.1 模型尺寸及边界条件确定

为获取滑坡作用下输油管道力学行为，建立基于SPH-FEM 算法的完全耦合模型，因模拟时耗，选取小型滑坡进行分析，且考虑滑坡体两侧非滑区域对管道受力的影响，以1：1 的比例建立非滑坡区域，其模型相关尺寸如图1 所示，其中管径为φ 508 mm×12 mm。

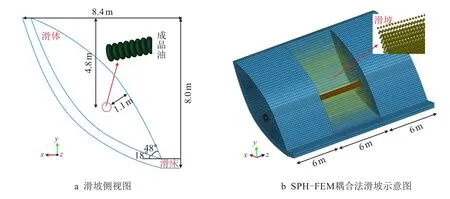
图1 基于SPH-FEM 法耦合模型尺寸Fig.1 The coupling model size based on SPH-FEM method

针对边界条件，模型顶面为自由面，而为避免边界处反射波对求解精度的干扰，在其滑坡床底部及其侧面设置无反射边界，同时，为了防止模型因全局重力加速度而发生下滑，在其底部施加全位移约束。

2.2 载荷施加及土-管-油耦合实现

滑坡是在自然环境（雨水、地震等）及人为因素干扰下，斜坡上岩/土体因重力作用，致其剪切应力超过材料本身的容许值时而发生的滑移现象。因而，本文为贴合于实际工况，考虑模型整体重量载荷，引入与时间相关联的重力加速度，对滑坡的演变过程最大程度进行复原，且相比于把管内成品油重量以外载形式施加于管壁部分节点有着更高的精度；对于管内成品油，分别设置内压为10 MPa，并施加沿z轴正方向1.5 m/s 的初始流速。

对于土-管-油耦合的实现，通过设置接触的形式完成，即通过Nodes To Surface 接触算法定义SPH粒子（滑坡体和成品油）为从体，FEM 网格（管道）为主体，选取自动接触类型，设置接触时间段，并考虑接触界面处土-管、管-油接触摩擦的影响，引入摩擦系数参数。同时采用罚函数进行接触界面的防穿透约束。

2.3 材料本构模型的选取

2.3.1 土体材料

土体材料选取MAT_FHWA_SOIL 模型，该模型采用修正后的Mohr-Coulomb 屈服准则，避免了尖端奇异性[14]。其表达式为

其主要参数见表1[14-15]。

表1 土体材料主要参数Tab.1 Main parameters of soil materials

2.3.2 管道材料

管道材料采用随动硬化双线性弹塑模型MAT_PLASTIC_KINEMATIC，其屈服强度为σy可定义为

其主要参数见表2。

表2 管道材料主要参[15-16]Tab.2 Main parameters of pipeline materials[15-16]

2.3.3 成品油材料

成品油材料采用MAT_NULL 模型，考虑流体动态粘度的同时，不需计算偏应力，并结合EOS_GRUNEISEN 状态方程来描述体积变形与压力间的关系，其表达式如式（5）所示，主要参数可见表3、表4。

表3 成品油材料参数[17]Tab.3 Material parameters of oil body[17]

表4 成品油状态方程参数[17]Tab.4 Oil body equation of state parameter[17]

2.4 有限元单元的选取及网格划分

对于滑坡体和管内成品油，选择无网格的SPH粒子，对于滑坡床和管道，选择8 节点的SOLID164体单元。并经试算后，滑坡体区域网格长度划分为15 cm，滑坡床区域划分为20 cm，共形成45 918 个SPH 粒子及56 880 个SOLID164 体单元。

3 数值模拟结果分析

3.1 滑坡下管道力学响应分析

图2a 为管道上各节点位置图，其中节点A1、B1 和C1 位于管道顶部，节点A2、B2 和C2 位于管道底部。

由图2b、图2c 可知，管道上各点沿x、y 向位移趋势基本相同，在初始时刻，各点位移量较小，随时间延伸，受土管油作用及周界处固土阻碍，致使沿线各点位移以不同速率增长，最后趋于稳定；且位移最大值点出现在管道中部（即滑坡宽度中心截面处），节点A1 处x向位移最大值约为3.08 cm，y 向最大值约为2.90 cm；节点A2 处x向位移最大值约为2.45 cm，y 向最大值约为2.13 cm。

图2 各节点位置位移时程曲线Fig.2 Position of each node and displacement time history curve of each node direction

将管道顶部与底部各节点x、y 向位移进行对比发现，顶部各节点位移显著大于底部；相同时刻下，当由管道中部向周界处延伸时，其位移差值逐渐增大。在周界处x向上，节点位移差值均值约为33.37%，y 向上为41.37%；综合x、y 向位移增量可知，在滑土作用下，管道受其扭转作用，整体沿z轴顺时针方向偏转，获取不同时刻下管体的总位移云图。由图3 可知，管体产生的变形具有较好的对称性，其对称轴处在管道中部处；当滑坡体后缘土体总位移量（以下简称为滑坡位移量）为35.00 cm 时，其位移最大值为4.11 cm，在滑坡后期，其位移量增至48.00 cm，管道位移增量不明显，趋于稳定。

图3 不同时刻下管道位移云图Fig.3 Pipeline displacement nephogram at different time

由图4 可知，在滑坡初始时刻，由于较小的下滑速度，致使管周滑土间并未出现相对滑动；随时间推移，后缘土体下滑同时受管道阻碍作用，致其临近土体发生剪切破坏，出现相对滑动，并通过调整自身应力分布形式将滑坡推力向管壁传递[18]，并最终趋于稳定。

图4 不同时刻下滑土状态图Fig.4 Slide soil state chart at different time

在管道迎/背滑坡面各取3 个单元，各单元位置如图5a 所示。

由图5b 可知，针对不同单元，应力最大值出现在单元D1 处，且在单元F2 处仍存在较大的应力值；在ts=800 ms 时，σD1≈340.29 MPa，此时已发生塑性形变，而σF2≈262.63 MPa，无失效风险。

图5 各单元位置及应力曲线Fig.5 Location and stress curve of each element

其主要原因在于，当滑坡发生时，滑土产生的推力直接作用于迎滑面，此外管道中部远离周界，受其周界处固土支撑作用较小；而针对于F2 处，管体受冲击的同时，整体产生沿y 轴负向的位移。

而在滑坡床内侧，由于固土的存在，阻碍管体进一步运动，进而在滑坡床端背滑面产生较强的管土作用，是与实际工况相符的。其余各单元应力时程较稳定，其值在179～220 MPa。获取不同时刻下管道应力云图，由图6 可知，在迎滑坡面管道中部及背滑坡面滑坡床内侧都出现明显的应力集中现象，验证了上述的说明；且随着滑坡位移量的增大，管道所产生的应力值也越发接近屈服强度。

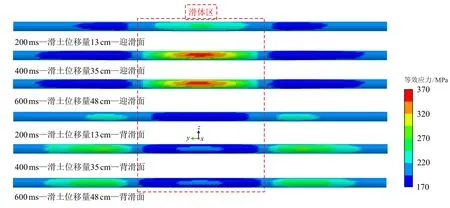
图6 不同时刻下管道应力云图Fig.6 Pipeline stress nephogram at different times

由图7 可知，不同工况下，各节点总位移时程曲线趋势基本相同，即在滑坡演变过程中，各点位移先逐渐增大而后趋于稳定；各工况下，位移最大值点均出现在管道中部A1 处。

图7 不同工况下各节点总位移时程Fig.7 The total displacement time history of each node under different working conditions

但在工况1 情况下，其位置出现一定角度的偏转（如图8 位移云图所示），此外由中部向周界处延伸时，各点位移量逐渐减小。对比各工况下节点位移曲线发现，在ts＜250 ms 段内，工况3 下各点位移曲线均小于其余工况，当ts＞250 ms 时，位移量逐渐反超，说明管内成品油的作用由初始时刻的“抗变”转变为“助变”；在稳定段（ts为600～1000 ms）内，较之工况1、2 及4，节点A1 处（差值均值）分别增长了17.57%、10.63%及13.04%。对比工况2 与4 发现，各点位移曲线较为接近，稳定段小于2.70%，说明当管内成品油量相对较少时，其自身重力影响较小，因而可根据实际情况，进行简化处理。

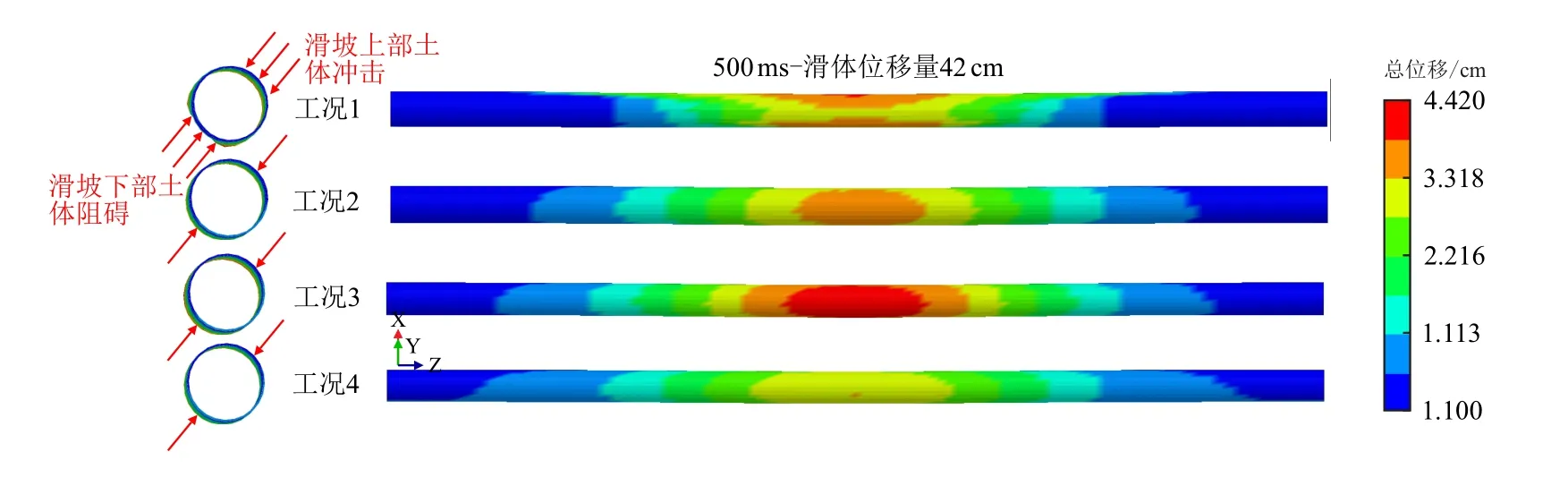
图8 不同工况下管道位移云图及其截面变形图Fig.8 Pipeline displacement nephogram and section deformation diagram under different working conditions

由图9 可知，相比于工况1，其余工况下应力曲线趋势基本相同。在迎滑面345°处出现应力最大值；针对于工况3，σ≈347.40 MPa，较之工况2、4 分别增长4.96%、8.83%，与位移增量相比缩小1 倍左右，可见满管工况下管内成品油作用对其位移产生更大影响；而针对于工况1，σmax=184.9 MPa，缩小近1 倍，其主要原因在于管内壁无输送介质所提供的压力，且由于土体滑动速度的不同，在滑坡后缘土体冲击及前缘土体阻碍作用下，致其管截面发生明显的不规则变形（如图8 管道截面图所示），在一定程度上抵消了滑土对管道的挤压作用。而其余工况管截面变形较为均匀，呈现出“椭球”状。

图9 不同工况下各截面应力曲线Fig.9 Stress curve of pipeline section under different working conditions

3.2 管道参数对其力学影响

为探究管道埋深对其力学响应的影响，建立滑坡区长为9 m（滑床区域两侧各为9 m）的模型，管径φ 508 mm×12 mm，埋深分别为0.6、1.1 和1.6 m，并保证除埋深之外的基本信息一致性。

其中，图10a 为节点位置图，A1 点位于管体顶层端，A2 为管体底层端。由图10b 可知，在ts为0～350 ms 时段内，不同工况下相同位置处各点总位移基本重合，说明在滑坡初始时刻，埋深变化所带来的影响较小，同时验证管道只受周围一定范围土体影响；随时间推移，滑坡后缘土体向管周积压，促使管土作用进一步增强，进而不同埋深处管道逐渐出现位移偏差。随埋深的减小，其位移量增大，原因在于管道敷设于滑坡体中央，滑坡体倾角较大，滑土具有沿x轴负向移动趋势（如图10c 所示），致使浅埋管道更易受到侧方来土的推挤作用，而相比于埋深为0.6 m 情况下，埋深为1.1 m 和1.6 m 时，管道各节点位移已向稳定趋势发展；ts=1 000 ms 时，埋深为0.6 m 下，XA1≈42.78 cm，较之埋深为1.1、1.6 m 分别增大34.88%、52.04%。

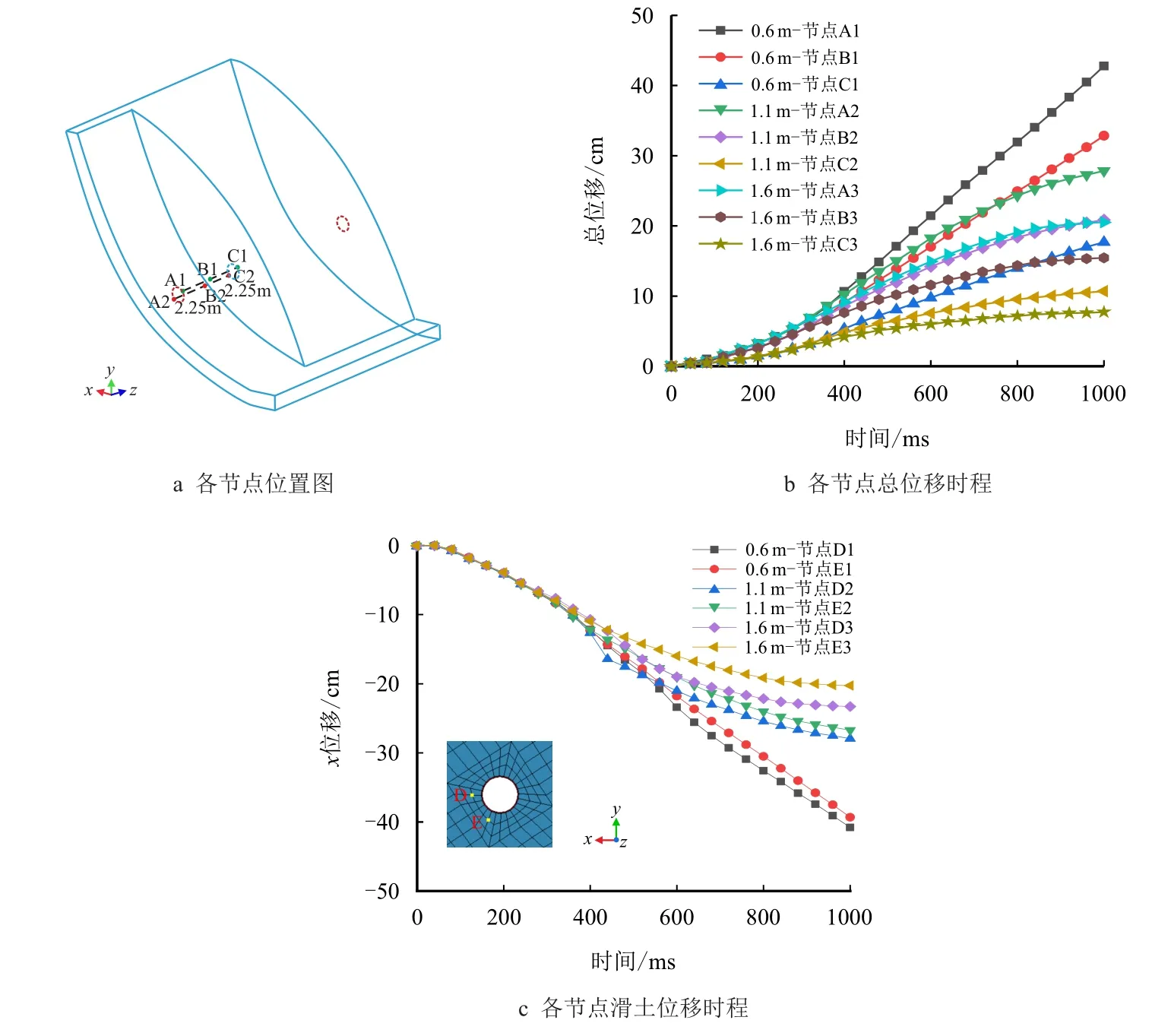
图10 管道各点总位移时程曲线及滑土x 向位移时程Fig.10 Time history curve of total displacement at each point of pipeline and X-displacement time history of sliding soil

由图11 可知，不同埋深下管道不同截面处应力曲线具有良好的对称性。

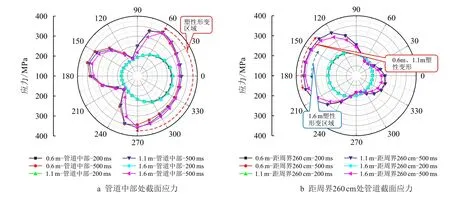
图11 不同埋深下管道不同截面处应力Fig.11 Stress at different sections of pipeline under different buried depth

当ts=200 ms 时，在滑体及油体作用下，管体各截面处所产生应力值较为均匀，呈现出“椭圆”状，随时间延伸，滑土进一步推挤管道，致其中部迎滑面及距周界一定距离的滑床背滑面处管土相互作用明显，不同截面处管道迎、背滑面产生的应力值较大偏差。

为探究径厚比带来的影响，分别选取管径为φ 508 mm×12 mm、φ 402 mm× 12 mm 及φ 273 mm×10 mm3 种工况。选取管道顶层及底层处沿线节点，获取其轴向总位移曲线。

由图12b 可知，不同径厚比下，管道位移曲线形状相似，且浅层端位移量较大；在周界处，由于过大的滑土冲击，管道产生明显位移，管周固土发生挤压变形与表面隆起；随径厚比的增大，其轴向位移减小。由图12c 可知，在相同的滑坡规模下，当管径增大时，虽管土作用接触面积变大，但对滑土产生的阻碍作用也是十分明显，致使滑土向稳定趋势发展，从而消减了滑坡体对管道的挤压作用。

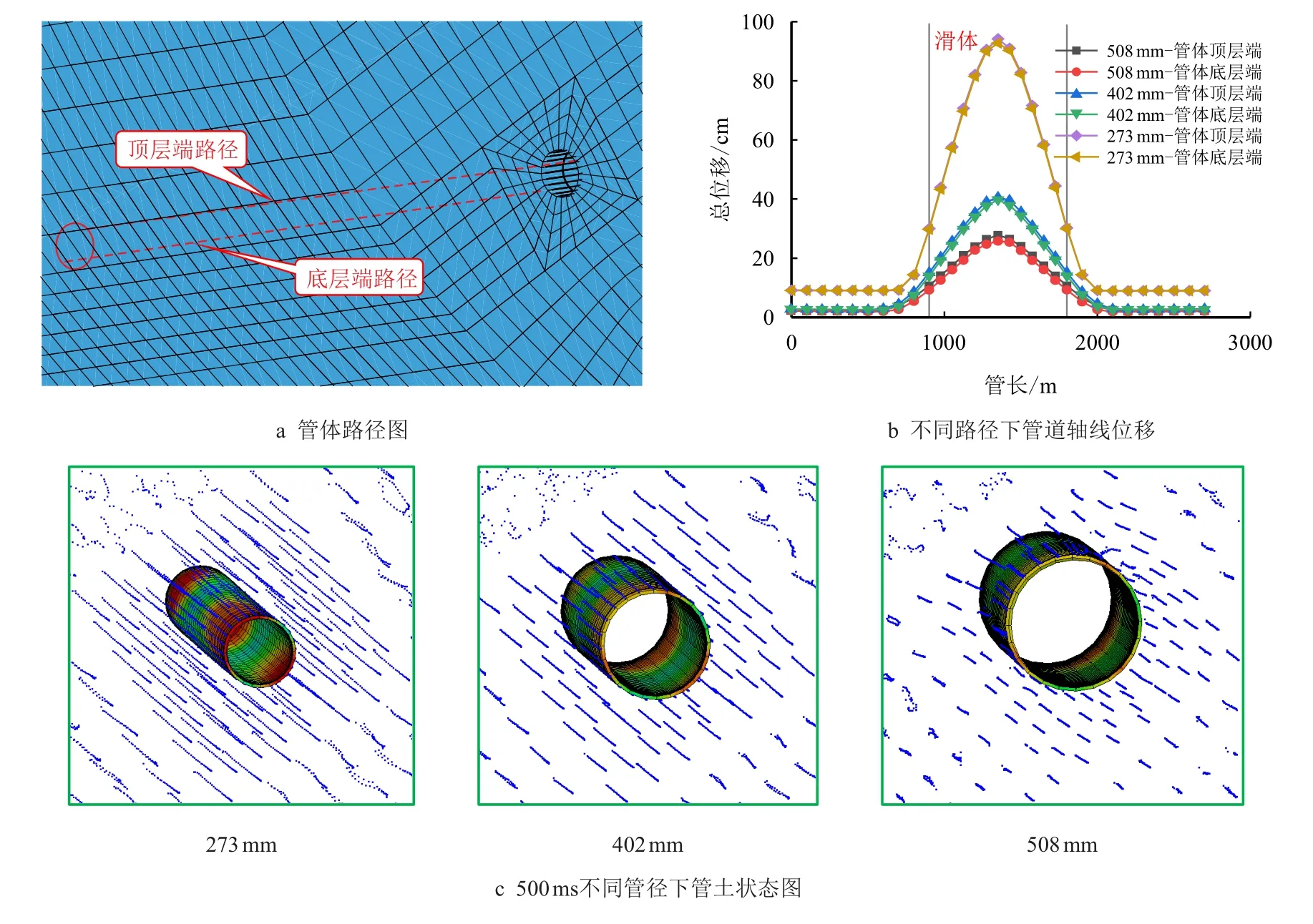
图12 不同径厚比下管道轴向位移与管土状态图Fig.12 Axial displacement of pipeline with different diameter-thickness ratio and diagram of pipe-soil state

由图13 可知，ts=200 ms，管径为508 mm 下，其截面应力最大，原因是滑坡初始时刻，滑土冲击力较小，管土接触面积起着主导作用。ts=500 ms，管径为273 mm 下，其截面应力值较大。

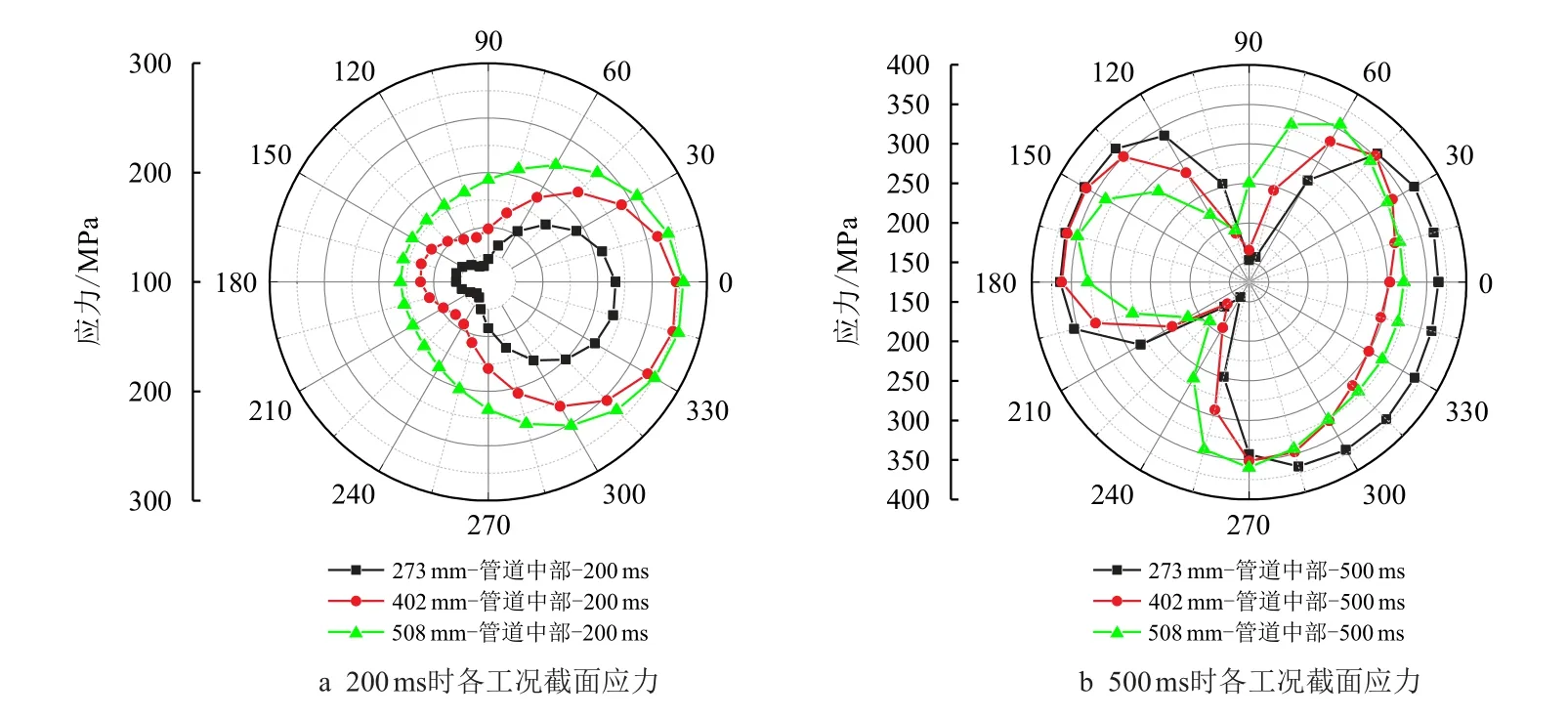
图13 不同时刻下管道截面应力曲线Fig.13 Stress curve of pipeline section at different time

且在迎/背滑面均出现多处塑性应变区域，是与上述情况相反的，说明随着时间的推移，管道阻碍作用起主导作用。

3.3 滑坡规模对管道力学影响

为探究滑坡规模对其影响，建立滑坡区长为6（滑床区域两侧各为6 m）、9（滑床区域两侧各为9 m）和12 m（滑床区域两侧各为12 m）的模型，管径为φ 508 mm×12 mm。

如图14 所示，保证了除滑坡规模之外的基本信息一致性。

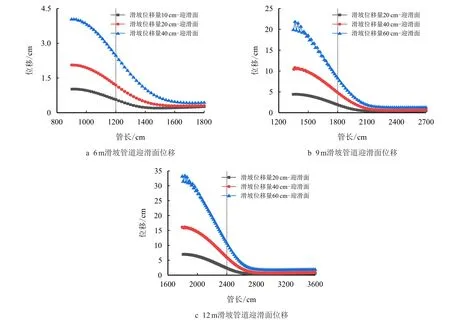
图14 不同滑坡规模及滑坡位移量下管道迎滑面轴向位移Fig.14 Under different landslide scale and landslide displacement,axial displacement of facing sliding surface of the pipeline

随着滑坡位移量增长，管道轴向位移均呈现增大趋势；滑坡规模6 m，滑坡位移量10、20 和40 cm时，管道中部位移分别约1.02、2.06 和4.05 cm，同理其规模为12 m 时，其中部位移分别约为6.99、16.13和33.24 cm；通过上述数据对比发现，当其位移量成倍增长同时，管道位移量也以近似相同的倍数进行增长；通过对比相同滑坡位移量、不同滑坡规模位移曲线发现，针对于同一管道，当滑坡规模达到一定量时，管土作用增大不再明显，使其位移增量减少；通过模拟发现，当滑坡长6 m，滑坡位移量为40 cm 时，由于管道的阻碍作用，滑坡体已向趋于稳定趋势发展，而随着滑坡规模的进一步增大，阻碍作用减弱，滑坡体冲击作用进一步增强，致使管道产生更大的形变。由图15 可知，不同滑坡规模及滑坡位移量下，迎滑面处应力最大值出现在管道中部，且随滑坡位移量的增大而增长；当滑坡长6 m，滑坡位移量为20、30 和40 cm 时，其应力分别为277.17、319.15 和332.27 MPa，此时各节点处均未达到屈服强度，而对于滑坡长9、12 m 时，滑坡位移量为30、40 cm 时，应力值较为接近，在360.00 MPa附近波动，皆以发生塑性形变；当滑坡规模逐渐增大时，在滑坡床内侧出现应力集中现象（如图中应力云图所示），其位置均出现在距周界2 m 处，且随着滑坡位移量增大，应力集中现象明显，当滑坡长12 m，滑坡位移量为40 cm 时，滑坡床处应力最大值为255.19 MPa，较之滑坡位移量30、20 cm 增长了18.30%、27.52%。针对于滑坡床处的应力最小值点，通常由1 个转变为2 个，且随着滑坡位移量的增大，其位置具有沿管道向两端移动的趋势，如滑坡长12 m 时，应力最小值点位置由2.72 m（滑坡位移量20 cm）增大到2.88 m（滑坡位移量40 cm）,且对于不同工况，其值均近似为180.00 MPa。

图15 不同滑坡规模及滑坡位移量下管道迎滑面轴向应力Fig.15 Under different landslide scale and landslide displacement,axial stress of facing sliding surface of the pipeline

4 结论

（1）SPH-FEM 耦合算法在解决传统网格法求解面临的难题，同时能更好的实现滑土与管体间滑移与粘着状态这种非线性转化的模拟，进而较好的再现管土作用，且滑坡体后缘土体会促使管周土体进一步积压、推挤管道，因此，为了获取更合理结果，进行完全耦合建模分析是非常有必要的。

（2）在滑坡作用下，相比于简化的成品油管道（只考虑内压），其成品油的存在，对管道力学行为规律并无较大变化，具有相似性，即管道变形近似为“鞍”状，在迎滑面管道中部及背滑面周界端出现应力集中等典型损伤行为。但对于文中工况，在满管工况下，管内成品油的作用由初始时刻的“抗变”转化为“助变”，且相比于管体所受应力，对其位移产生的影响更大，与简化为内压的空管相比，位移增加了10.63%（应力增加了4.96%），因而，对于管内成品油是否可进行简化处理，取决于滑坡规模与介质量，应根据具体实际工况进行取舍。

（3）当管道敷设于滑坡中部时，其位移量、塑性变形区域均随埋深的减少而增大；随管道径厚比的增大，其轴向位移减小，对其应力，在滑坡后期，由于管道对滑坡体阻碍作用起主导，致使大管径应力值降低明显；管道位移、应力均随滑坡位移量、滑坡规模的增大而增大。

符号说明

x空间位置距离，m；

x-x′粒子间距离，m；

mj粒子的质量，kg；

ρj粒子的密度，kg/cm3；

h光滑影响区长度，m；

w(x-x′,h)光滑函数；

p压力，MPa；

c内聚力，MPa；

J2应力偏张量的第二不变量，MPa2；

Ahyp屈服面间相似因数，MPa；

σ0初始屈服应力，MPa；

εPeff有效塑性应变，无因次；

σy屈服应力，MPa；

Ep塑性硬化模量，MPa；

P压力，Pa；

S1、S2和S3νs-νp曲线的斜率系数，无因次；

C曲线截距，m/s；

a一阶体积修正量，无因次；

ρ0初始密度，kg/cm3；

E能量密度，J/m3；

γ0Gruneisen 常数，无因次。