柔性石墨烯薄膜压力传感器力敏特性仿真计算

江天炎，张 程，曾 帅，毕茂强，陈 曦

(1.重庆理工大学 电气与电子工程学院，重庆 400054，2.新疆大学 电气工程学院，乌鲁木齐 830047)

近年来，随着可穿戴设备的研究进展，各类柔性传感器得到了广泛研究[1-3]。其中，具有柔性特征的敏感材料也成为该领域的重要研究内容。2004年，Geim团队采用机械剥离的手段第一次获得了单层石墨烯[4]。石墨烯材料的力学特性非常突出，除了它的杨氏模量非常高之外，石墨烯材料的硬度也很高，断裂强度为130 GPa，弹性常量达到了5 N/m。石墨烯材料的这些性质表明，使用石墨烯材料作为压力传感器的敏感单元在理论上有非常大的优势。目前已经有研究表明，石墨烯材料在1%的应力作用下便能作出反应，使自身的带隙打开而产生电能，从而实现力学与电学的直接转换。室温下，石墨烯材料的电子迁移率高达15 000 cm2/(V·s)[5]，热导率为5 000 W/mK[6-7]，杨氏模量可达1 TPa[8]。这些优异的性质使得石墨烯在各类传感器领域有广泛的应用前景[9-11]。

目前，不少学者在该领域的研究取得了进展。Smith A D等[12]研制了一种悬浮式的石墨烯压力传感器，在外施压力的作用下，其灵敏度仅为2.66×10-5kPa-1，工作范围为100 kPa。王萍萍等[13]提出了一种三维柔性石墨烯压力传感器，响应时间为75 ms，恢复响应时间为112 ms，但灵敏度只有0.013 kPa。李伊梦等[14]在2020年提出的石墨烯/PDMS仿生银杏叶微结构柔性压阻式压力传感器具有1.56 kPa的灵敏度和20 kPa的工作量程。由此可以看出，现阶段的石墨烯压力传感器难以同时满足高灵敏度和大量程的需求，而这主要取决于敏感材料的各项特性与传感器的结构设计。因此，研究石墨烯材料的敏感特性及传感机理具有重要意义。

本文中依据鼓泡试验原理建立石墨烯矩形薄膜的数学模型，得到压力载荷与最大形变、最大应变之间的数学关系；通过有限元分析法对石墨烯敏感材料建模分析，获取石墨烯矩形薄膜在压力载荷作用下的载荷-最大形变及载荷-最大应变关系；通过对比Beams球壳模型的解析解，验证模型的准确性；基于石墨烯矩形薄膜的模态分析，仿真计算得到石墨烯矩形薄膜前6阶的固有频率及振型图。讨论了不同厚度石墨烯矩形薄膜的前6阶固有频率，为石墨烯压力敏感器件的设计制作提供理论参考。

1 石墨烯薄膜力学特性建模

鼓泡试验法(bulge test)是一种分析薄膜力学性质的手段，Beams在此基础上提出了薄膜的球壳模型，将薄膜受力形变后的模型视作薄壁球壳[15]。根据载荷与形变结果来确定材料的各项参数，仿真计算时依据材料的杨氏模量和泊松比等参数来计算模型的最大形变和应变。

参考鼓泡试验法建立石墨烯矩形薄膜的理论计算模型[16]，其中矩形薄膜的短边为a，长边为b，薄膜厚度为h。薄膜四边固定，在垂直于薄膜的平面施加一个均布载荷p，薄膜受力形变如图1所示，产生的最大形变w在薄膜中心处，薄膜的曲率半径为R。

图1 矩形薄膜截面示意图

首先，依据鼓泡试验原理可知[15]，外界施加的压力p与矩形薄膜内二向应力σ保持平衡，所以有：

σ*2h*b=p*2R*b

(1)

化简式(1)即可得到：

(2)

由于矩形薄膜受力后产生的形变量远小于短边长，因此薄膜的曲率半径可表示为：

(3)

结合式(2)(3)，矩形薄膜内二向应力σ可表示为：

(4)

根据力学特性，薄膜表面张力可表示为：

(5)

薄膜的应变大小可表示为：

(6)

然后，将式(3)代入式(6)计算，整理后可得矩形薄膜的应变为：

(7)

对于矩形薄膜而言：

(8)

根据二向应变得到表面张力为：

(9)

结合式(7)(9)，可得压力差导致的矩形薄膜表面张力为：

(10)

表面总张力为初始表面张力与压力差导致的表面张力总和，即：

(11)

整理后得到矩形薄膜所受压力与最大形变的关系为：

(12)

结合式(7)(11)，可得压力与应变之间的关系为：

(13)

其中：σ0为薄膜初始预应力；v为泊松比；E为弹性模量；h为石墨烯薄膜厚度；ω为薄膜的最大形变。

由式(12)和(13)得到压力p与薄膜形变、应变的关系，这里通过给定薄膜的参数值，计算得到方程的解析解。取石墨烯矩形薄膜的短边长a=9 μm，v=0.16，E=1 TPa，单层石墨烯厚度h=0.335 nm，σ0=0.3 GPa[17]，分别取压力载荷p=0、0.1、0.2、0.3、0.5、1、2、3、4、5 MPa，根据式(12)(13)计算得到的不同厚度的石墨烯矩形薄膜载荷-最大形变和载荷-应变关系如图2、3所示。

图2 不同厚度薄膜的载荷-最大形变关系

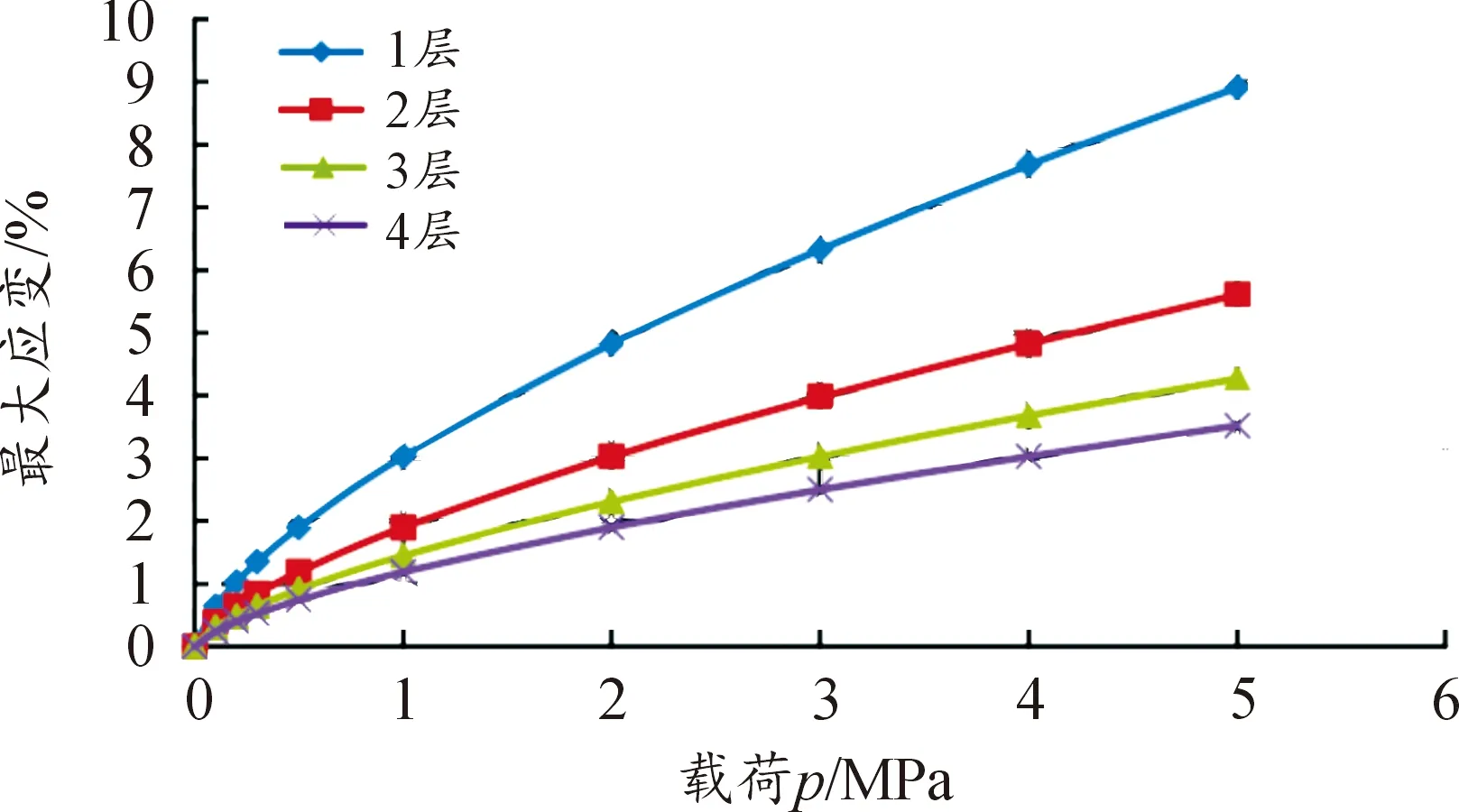
图3 不同厚度薄膜的载荷-最大应变关系

由图2、3的结果可以看出：在较低的载荷作用下，石墨烯矩形薄膜最大形变的变化率较大；随着载荷的增大，形变量和应变量会逐渐趋于恒值，且随着石墨烯厚度的增加，在相同载荷作用下其最大形变及最大应变都在逐渐减小，说明石墨烯薄膜厚度越薄，对外界载荷的感应越灵敏。

2 石墨烯薄膜有限元建模与仿真

2.1 有限元模型构建

通过有限元仿真软件COMSOL建立石墨烯矩形薄膜的有限元仿真模型。考虑到单层石墨烯材料的厚度很薄，结合Beams的球壳模型，采用软件COMSOL中二维模型下的plate接口进行仿真计算。对于矩形薄膜而言，当其长宽比大于5时，矩形薄膜受力后的形变与长宽比无关[18]，因此在建模时取长宽比固定为6，即短边长a=9 μm时，长边b=54 μm，单层石墨烯厚度h=0.335 nm。设定石墨烯材料的属性E=1 TPa、v=0.16、密度为2 200 kg/m3。在plate接口下还需将石墨烯设定为各向同性的线弹性材料，同时为其设定大小为0.3 GPa的初始预应力。矩形薄膜四周取固定约束，在其表面施加一个均布载荷p。网格划分时采取系统默认的较细化规格，研究计算时还需考虑到模型的几何非线性。由于薄膜受载荷作用后的形变远大于其厚度，属于大挠度变形，因此需要在默认的稳态求解器中选定几何非线性，以保证计算结果的准确性。

依据矩形薄膜受力后的力学理论[19]可知：四边固定支撑的矩形薄膜在载荷的作用下，最大形变为模型中心处的变形，最大应变发生在过模型中心点短边的截线处，如图4所示。

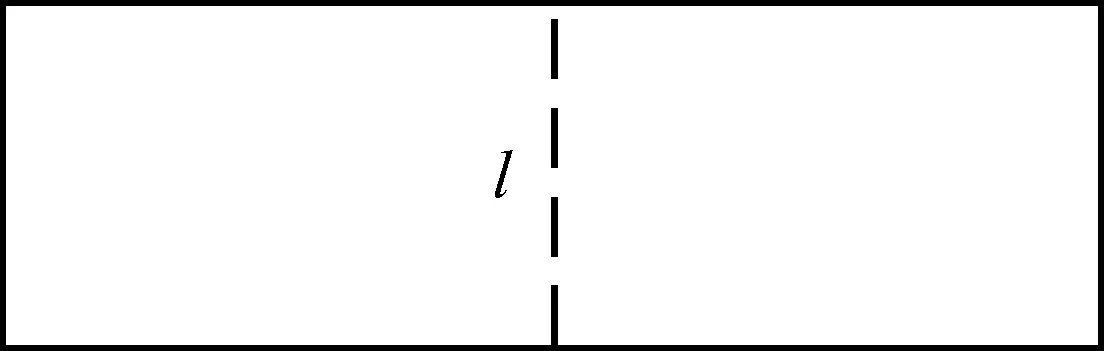
图4 矩形薄膜截线位置示意图

薄膜最大应变为：

ε=(Δl/l)*100%

(14)

式中：l为截线原始长度；Δl为形变量。

通过分析图4中截线在变形前后的长短变化，能得出薄膜受力应变。利用软件结果后处理来构建该条截线，导出截线上的坐标数据。利用Matlab拟合出该截线形变后的曲线，再利用曲线积分求出形变后的长度，便可求得应变大小[20]。

仿真时设置载荷q值为0.1 MPa，计算得到的石墨烯矩形薄膜结果如图5所示。从图5中可以看出，仿真计算得到的最大形变为0.444 3。根据上述的应变计算方法，先处理得到形变量Δl，最后得到的石墨烯矩形薄膜的最大应变值为0.64%。对于一般型传感器结构，当石墨烯薄膜受到均匀的压力时，位移主要发生在石墨烯薄膜的中心，应力主要分布在石墨烯薄膜的边缘。

图5 形变位移仿真结果

2.2 薄膜厚度对最大形变及应变的影响

考虑到不同石墨烯薄膜厚度对其敏感特性的影响，取薄膜层数为1、2、3、4层进行仿真计算。为与Beams模型解进行验证，同样取载荷p=0、0.1、0.2、0.3、0.5、1、2、3、4和5 MPa，在短边长为a=9 μm的模型下进行仿真，得到的结果如图6、7所示。结果表明，当施加的载荷在0.5 MPa以内时，各条曲线的斜率较大，表明该阶段石墨烯薄膜对载荷的反应较灵敏，而且在相同载荷下，单层石墨烯薄膜的形变以及应变都最大，表明单层石墨烯薄膜对载荷的反应较显著。

图6 不同厚度薄膜的载荷-最大形变仿真结果

通过与Beams模型解的比较发现：两者计算得到的载荷-最大形变及载荷-最大应变结果趋于一致；计算得到的载荷-最大形变及载荷-最大应变曲线的平均相对误差分别为4%和3%，表明仿真模型的准确性；随着薄膜层数的增加，平均相对误差越小，其对载荷反应的灵敏程度在减小。虽然随着薄膜厚度的增加，石墨烯载荷-最大形变特性曲线的曲率变小使得非线性得到相应改善，但对压力的敏感程度相对降低。

图7 不同厚度薄膜的载荷-最大应变仿真结果

2.3 薄膜尺寸对最大形变及应变的影响

讨论石墨烯薄膜的尺寸对其力学特性的影响，分别取短边长a=6、9、12、18。在单层石墨烯厚度下，施加载荷p=0、0.1、0.2、0.3、0.5、1、2、3、4和5 MPa，分析石墨烯薄膜的最大形变和应变，得到结果如图8、9所示。

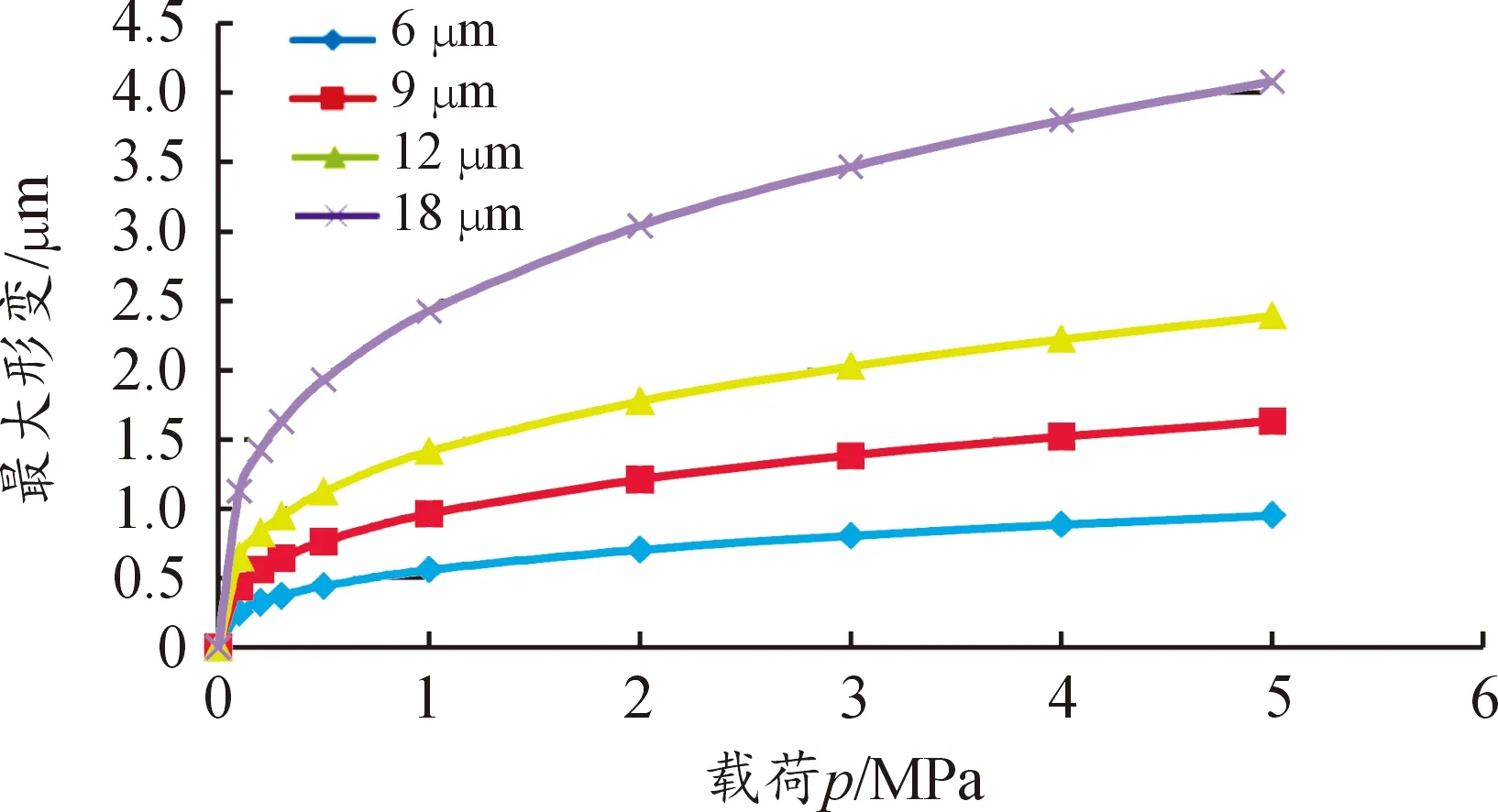
图8 不同尺寸薄膜的载荷-最大形变仿真结果

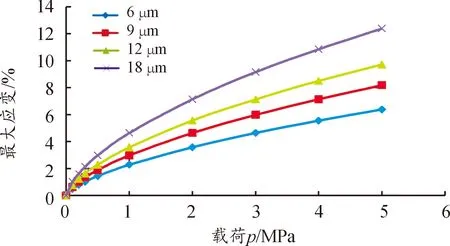
图9 不同尺寸薄膜的载荷-最大应变仿真结果

比较不同尺寸石墨烯矩形薄膜的仿真结果可知：矩形薄膜在固定的长宽比下，当施加同样的载荷时，石墨烯薄膜的尺寸越大，产生的最大形变越大，最大应变也越大，表明其对载荷的反应越明显；同样地，当施加的载荷较小时，曲线的斜率较大，薄膜对载荷的反应越灵敏。

通过与Beams模型进行对比，计算得到载荷-最大形变及载荷-最大应变曲线的平均相对误差分别为5%和2%，进一步验证了模型的有效性。随着薄膜尺寸的增大，平均相对误差越来越小，但其对载荷反应的灵敏程度在减小。对于石墨烯矩形薄膜，尺寸会影响石墨烯对载荷反应的灵敏度，但过大的尺寸会使其灵敏程度减小。

综合对比各曲线可知：对于石墨烯矩形薄膜而言，其尺寸越大、厚度越薄，显现出来的力学特性越明显。在载荷的作用下，产生的形变越大，相应的应变也越大，表明其对载荷的感应显著和灵敏。但是，在设计传感器敏感单元时，并非尺寸越大、越薄越好，还需考虑器件的工作范围。对于厚度更薄、尺寸更大的薄膜，其载荷反应敏锐，但易受外力影响而变形。且薄膜越薄，其测量范围相对更小，进而影响器件性能。因此，在制作石墨烯敏感器件时，需要考虑其制作工艺、运用场景来合理设计尺寸，使其满足相应工作场合的需要。

3 石墨烯薄膜模态分析

对于薄膜而言，在没有预张紧力作用时，由于它不具有弯曲刚度，故形状会与同它接触的表面贴合一致[21]。假设其布置的位置存在孔洞，那么该处的膜便会凹陷变型，因此在上述研究中，添加一个大小为0.3 GPa的预张紧力来进行分析。由于预应力会改变薄膜的固有频率，故在0.3 GPa的预应力下，研究石墨烯薄膜的固有频率和各阶振型，为设计石墨烯压力敏感器件提供理论参考。

同样，利用前文设计的有限元模型，选取短边长a=9 μm、厚度h=0.335 nm的模型，仿真得到石墨烯薄膜的固有频率和振型图。这里取前6阶为例，得到的振型图如图10、11所示。

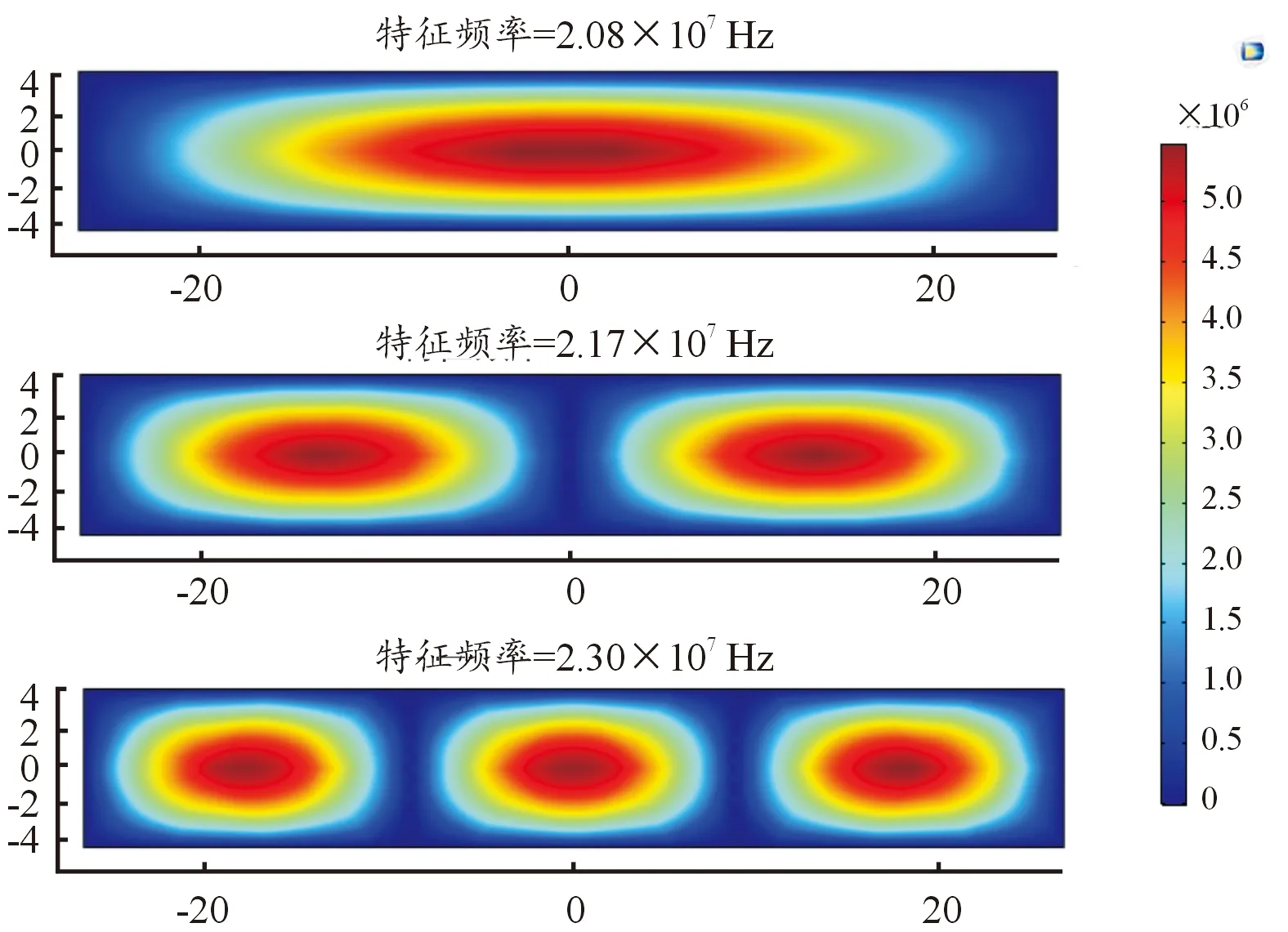
图10 石墨烯薄膜1～3阶振型图

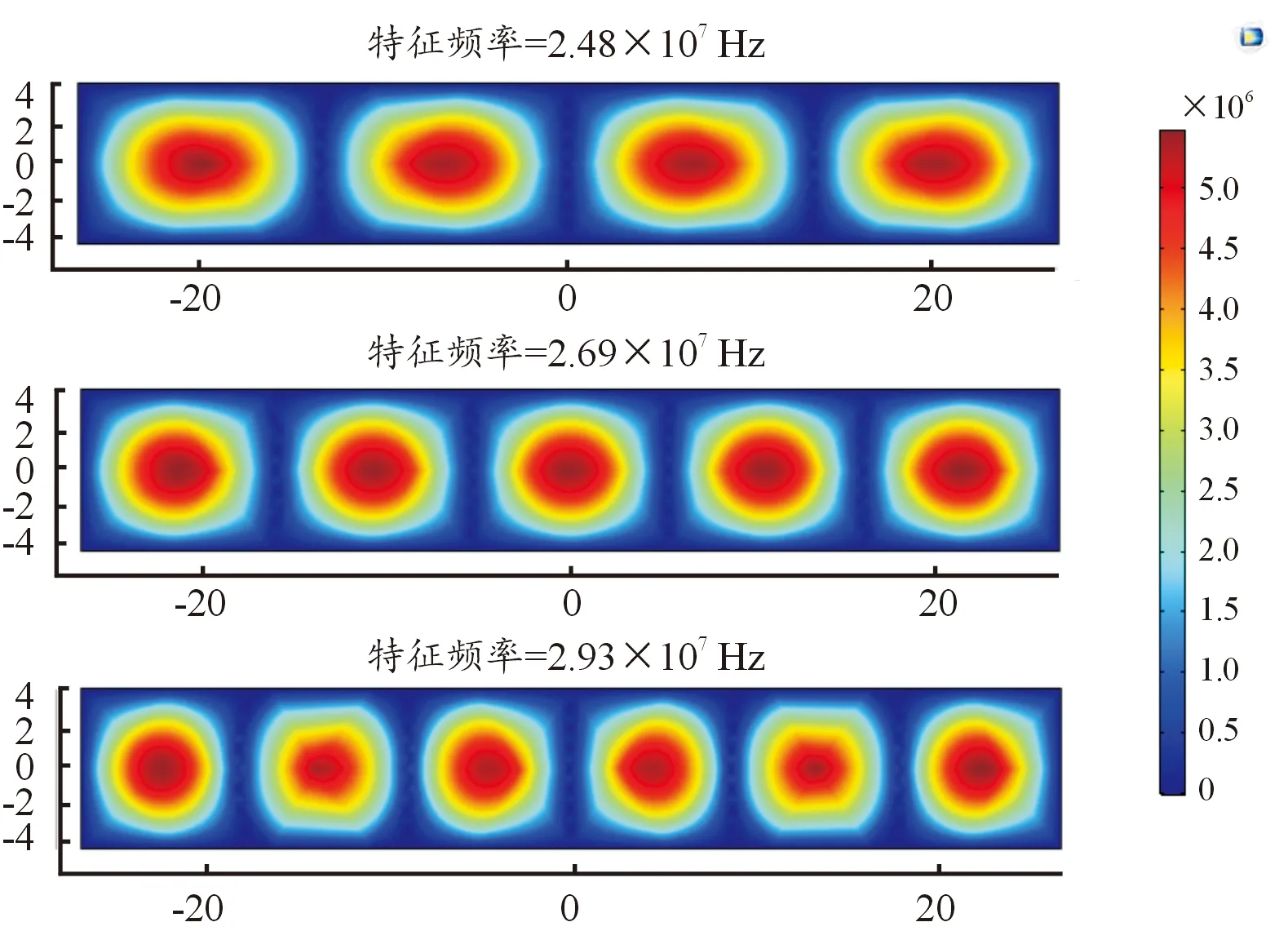
图11 石墨烯薄膜4～6阶振型图

从上述图例中可以看出：每种振型对应一个固有频率，随着阶数的增加，对应的振型也较复杂，相应的固有频率也随着增大。这是因为各阶的固有频率与石墨烯矩形薄膜厚度有关[22-23]。表1给出了1～4层厚度石墨烯薄膜的固有频率。随着石墨烯矩形薄膜厚度的增加，对应的各阶固有频率会随之减小。因为固有频率为物体本身的性质，除了与物体厚度有关以外，与物体的尺寸及密度等同样关系密切，因此在设计制造石墨烯压力敏感器件时，要综合考虑器件的尺寸及厚度，提升石墨烯薄膜自身的自振频率。同时，需尽量保证器件接触面的整洁度，使石墨烯敏感薄膜本身与结构表面接触有较大的预应力，减小外界干扰信号对石墨烯敏感结构的影响，在满足器件自身稳定的前提下，选取合适的厚度、尺寸来进行设计制造。

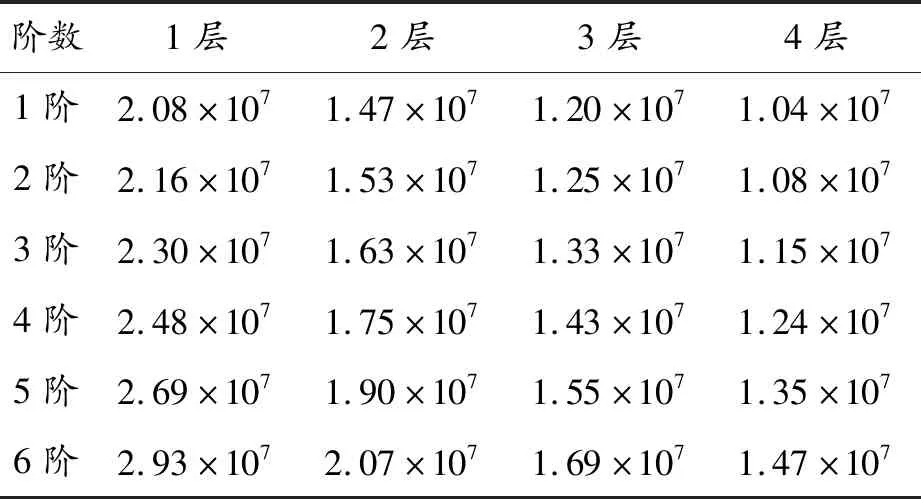
表1 不同层数石墨烯薄膜的固有频率 Hz

4 结论

1)基于Beams球壳模型，得到石墨烯矩形薄膜最大形变与应变的解析解、载荷-最大应变与载荷最大形变的数学关系。

2)在低载荷作用下，载荷-最大形变及载荷-最大应变曲线斜率较大，石墨烯薄膜对载荷反应较灵敏；石墨烯薄膜的尺寸越大、越薄，其对载荷的反应越显著，对应的形变及应变也越大；通过与Beams球壳模型得到的结果相对比发现，两者的平均相对误差在5%以下，表明了模型的有效性。

3)随着石墨烯薄膜厚度的增加，各阶的固有频率随之减小，但其所能承受的压力范围也越大，因此需要综合考量薄膜厚度、尺寸来设计满足需要的压力敏感器件。

通过对柔性石墨烯薄膜压力传感器力敏特性的仿真，验证了石墨烯薄膜模型的准确性。同时，对石墨烯矩形薄膜进行了模态分析，得到其前6阶固有频率与振型。分析了不同厚度石墨烯矩形薄膜的固有频率，为设计制造石墨烯压力敏感器件提供参考。