电动轮汽车对置布置磁流变减振器控制研究

刘晋霞，王 凯，耿 乐

(山东科技大学 a.交通学院;b.机械电子工程学院，山东 青岛 266590)

随着汽车电气化、智能网联化的发展，具有布置灵活、易于实现各种线控操纵的电动轮汽车被认为是最具发展潜力的电动汽车。其中集成有轮毂电机、制动器等结构的电动轮成为了电动轮汽车驱动系统的核心部件。然而，由于轮毂电机、制动器等结构的集成使得电动轮与传统悬架匹配安装不适应[1]，且非簧载质量增加导致整车平顺性下降[2]。因此，与电动轮相匹配的悬架结构改进及提高平顺性成为了诸多学者研究的热点。

针对电动轮与传统悬架匹配安装不适应问题，陈龙等[3]将麦弗逊悬架的单个下控制臂改为2个独立的控制臂。陈辛波等[4]在对悬架导向机构和转向机构进行优化设计的基础上，提出前、后双横臂悬架-扭杆弹簧-电动轮模块。George等[5]改进了悬架连杆结构及位置关系，得到了与电动轮匹配的新型悬架构型。此外，杨蔚华等[6-7]分别将单个和对置布置的磁流变减振器集成于电动轮内，改善了悬架干涉问题，同时提高了电动轮集成程度。由于磁流变减振器具有阻尼连续可调、磁流变液稳定性强等优点，为提高电动轮汽车的平顺性，不少学者针对该种减振器展开了电动轮汽车的平顺性控制研究。Nguyen等[8-11]基于一定路面等级[12]、匀速行驶条件，分别建立含有磁流变减振器的1/4电动轮车辆模型，采用自适应最优模糊滑膜、H∞鲁棒、变增益模糊控制、天棚模糊控制等方法来改善电动轮汽车的平顺性。

上述关于电动轮汽车平顺性的研究均以匀速行驶工况、20世纪80年代测定路面等级或特定隆起路面激励为基础，不能反映当今已高度发展的道路情况。由于在模糊控制的基础上增加伸缩因子控制论域伸缩的变论域模糊控制具有实时性好、精度高的优点[13]，而被应用于磁流变减振器控制研究中[14-15]。因此，本文基于对置布置磁流变减振器的电动轮汽车，建立1/4车辆模型，取高速沥青路面百公里加速、100 km/h匀速及郊区混凝土路面60 km/h匀速3种路面激励，设计模糊及变论域模糊控制器，展开对置布置磁流变减振器的控制研究，为电动轮汽车的设计提供了理论参考价值。

1 对置布置磁流变减振器1/4车辆模型

1.1 1/4车辆模型建立

根据对置布置磁流变减振器电动轮结构[7]，建立1/4车辆模型，如图1所示，图中，ms、mu分别为簧载质量、非簧载质量；ks、kt分别为悬架弹簧与轮胎的等效刚度；xs、xu、xr分别为簧载质量位移、非簧载质量位移、路面激励；Ce、FMR分别为磁流变减振器等效无场阻尼系数、库仑阻尼力。

图1 对置布置磁流变减振器电动轮1/4车辆模型

根据簧载质量、非簧载质量与磁流变减振器的连接关系，运用牛顿第二定律建立动力学公式(1)，车辆的部分参数取值见表1[16]。

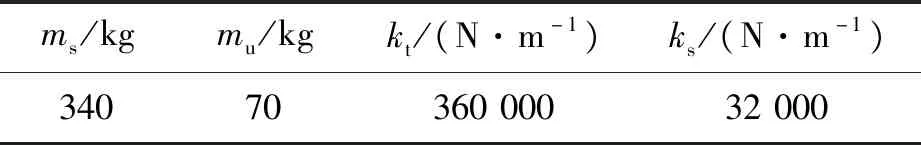
表1 车辆部分参数数值

(1)

1.2 单个减振器阻尼力计算

由于车辆悬架行程较大，此处磁流变减振器选用其流动和剪切模式共同作用的混合工作模式[17]，忽略内部摩擦力及流体惯性作用，其阻尼力Fd为：

(2)

1.3 路面激励计算

路面激励是引起车辆行驶过程中振动颠簸的主要因素，受到路面不平度及车辆行驶速度的影响。选取高速沥青路面百公里加速、100 km/h匀速及郊区混凝土路面60 km/h匀速3种路面激励，由式(3)[15]计算随机路面激励xr(t)，如图2所示。由图可知，高速沥青路面百公里加速、100 km/h匀速及郊区混凝土路面60 km/h匀速的路面激励逐渐增大。

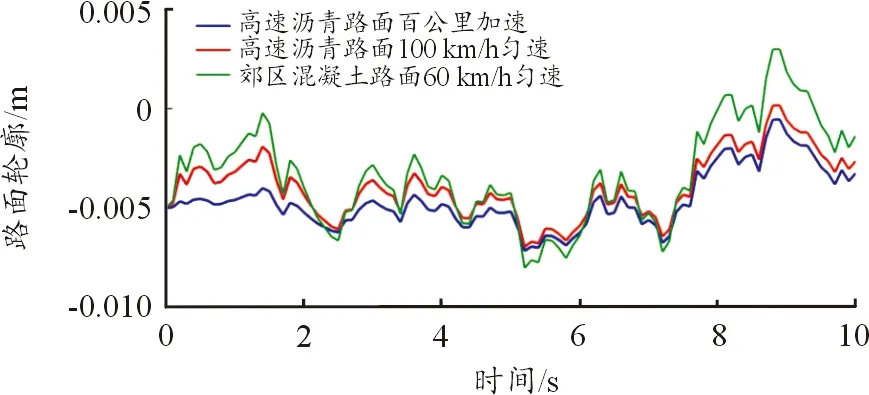
图2 3种典型行驶工况路面激励曲线

(3)

式中：f0为滤波器下限截止频率，取值为0.01；Gq为路面不平度系数，高速沥青与郊区混凝土路面的Gq分别取值为4、16[18]；v为车辆行驶速度，其中，百公里加速数据见表2、拟合速度为式(4)；w1为高斯白噪声。

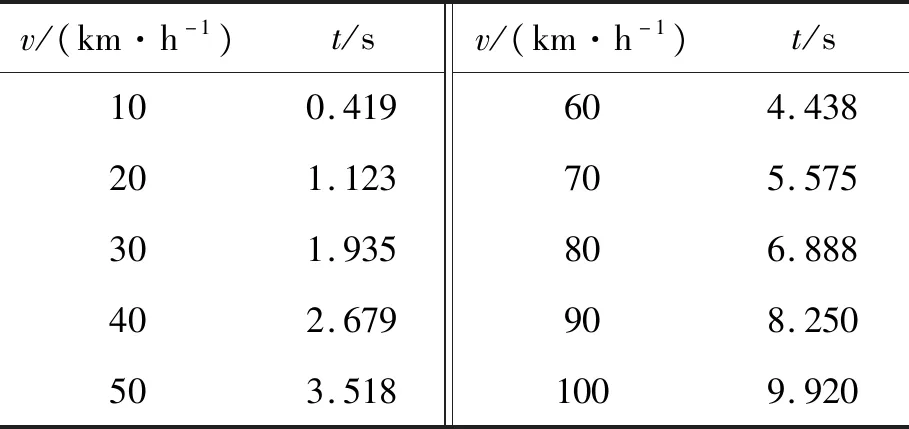
表2 某车辆百公里加速数据

v=0.033t3-1.052t2+17.14t+1.365

(4)

2 磁流变减振器控制研究

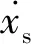
2.1 模糊控制

2.1.1模糊控制器设计

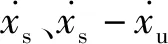
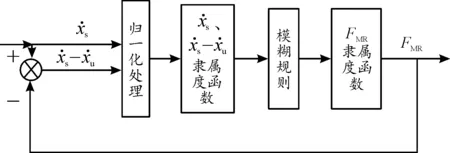
图3 磁流变减振器模糊控制器结构

2.1.2模糊控制过程

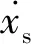
图隶属度函数

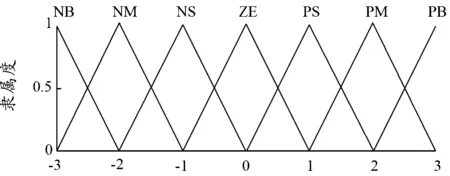
输出量FMR采用论域为[-3，3]的三角形隶属度函数，设置负大NB、负中NM、负小NS、零ZE、正小PS、正中PM、正大PB 7个模糊子集，隶属度函数如图5所示。

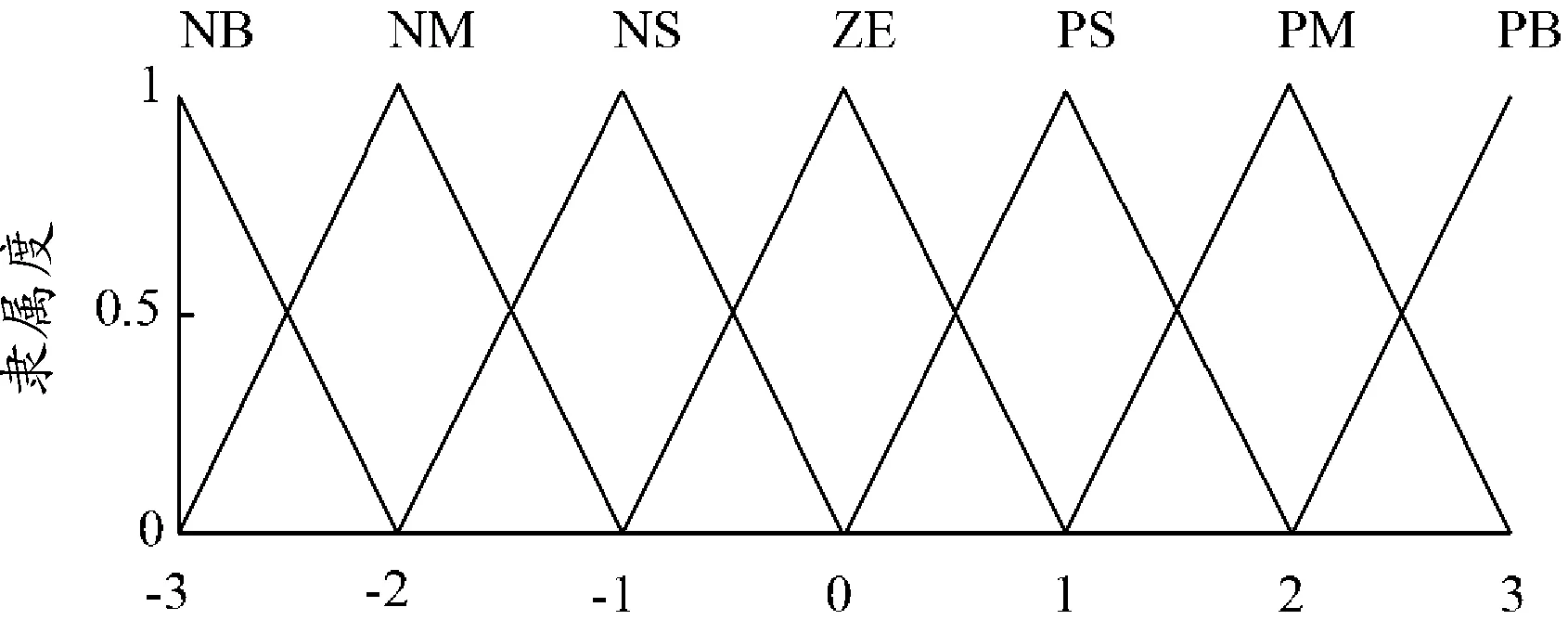
图5 FMR隶属度函数

采用响应快、出错少的Mamdani模糊推理法，模糊控制规则见表3。

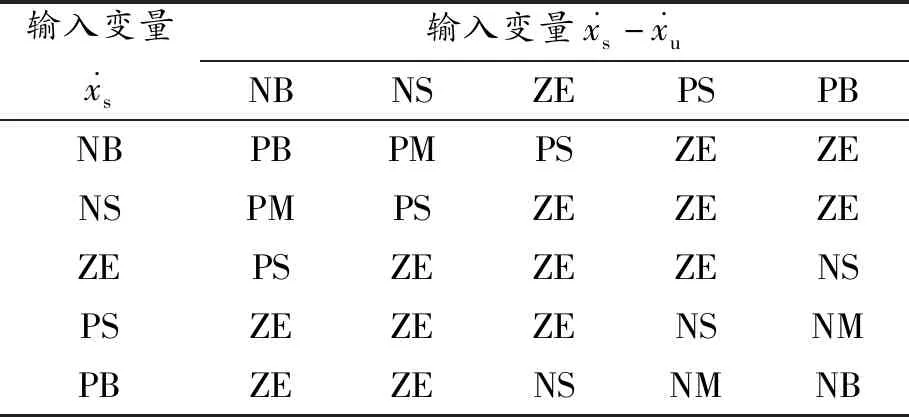
表3 FMR的控制规则

2.2 变论域模糊控制

2.2.1变论域模糊控制器设计

2.2.2论域调整

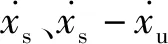
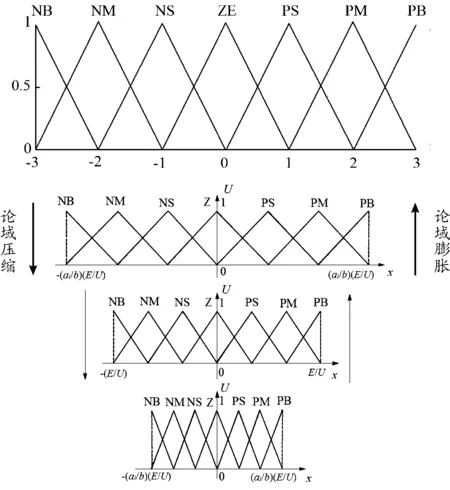
图7 论域调整原理示意图

2.2.3伸缩、量化及比例因子的计算

(5)

(6)

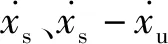
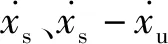
(7)

输出变量a1、a2、b的比例因子a1′、a2′和b′计算公式为：

(8)

2.2.4变论域模糊控制过程

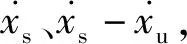
图隶属度函数

根据误差逐级逼近及专家经验对控制器参数调整，建立变论域模糊控制规则，见表4～6。

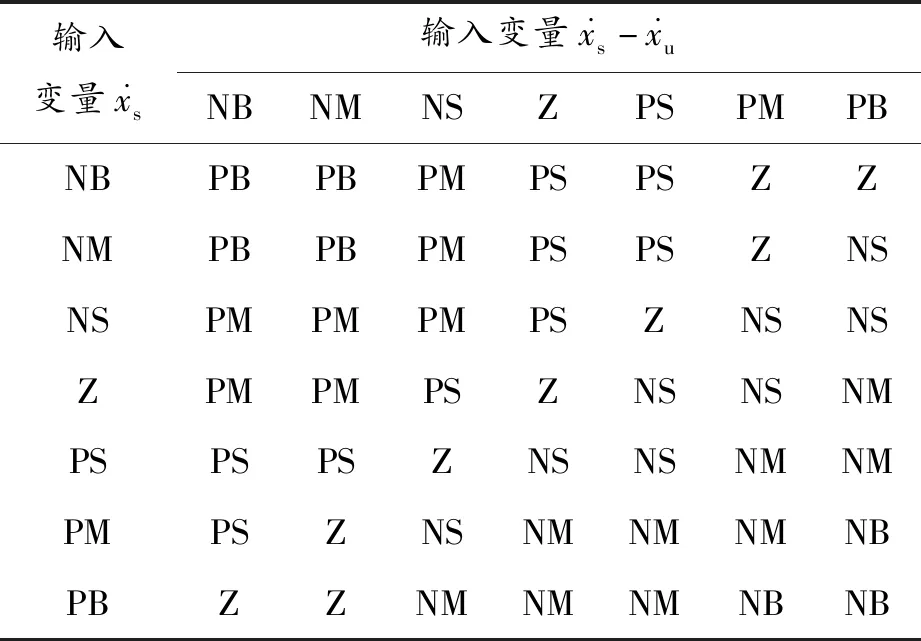
表4 a1的控制规则

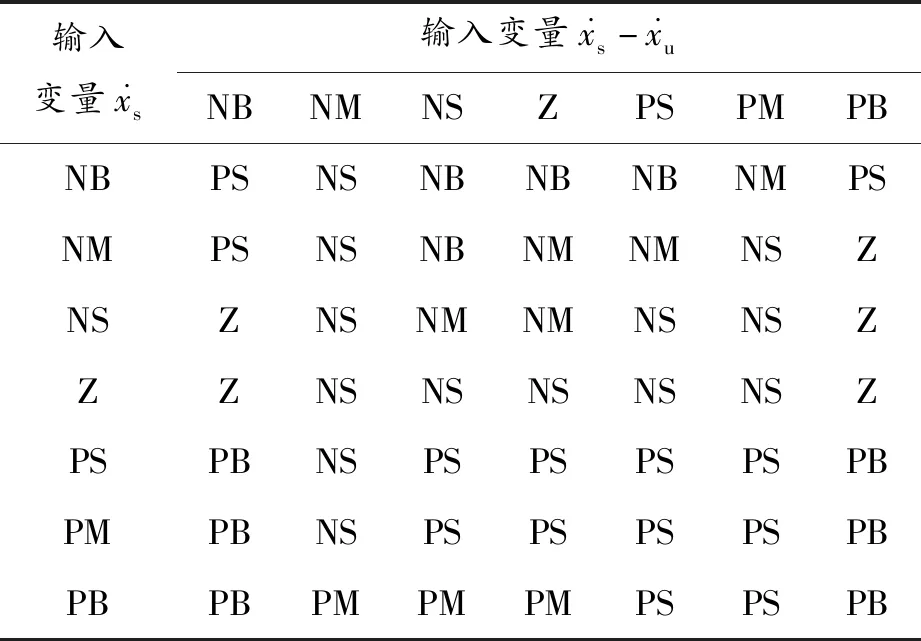
表5 a2的控制规则

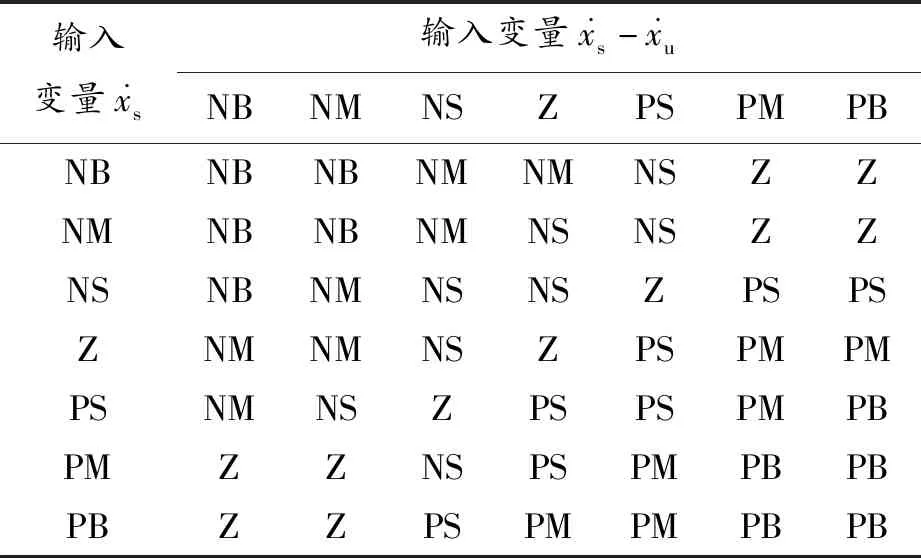
表6 b的控制规则

3 仿真及结果分析

在Simulink中搭建本文所建1/4车辆模型，分别导入模糊控制及变论域模糊控制器，仿真分析高速沥青路面百公里加速、100 km/h匀速、郊区混凝土路面60 km/h匀速3种路面激励下，车身加速度、悬架动行程、轮胎动载荷的时域如图9～11所示，统计其均方根值见表7～9。

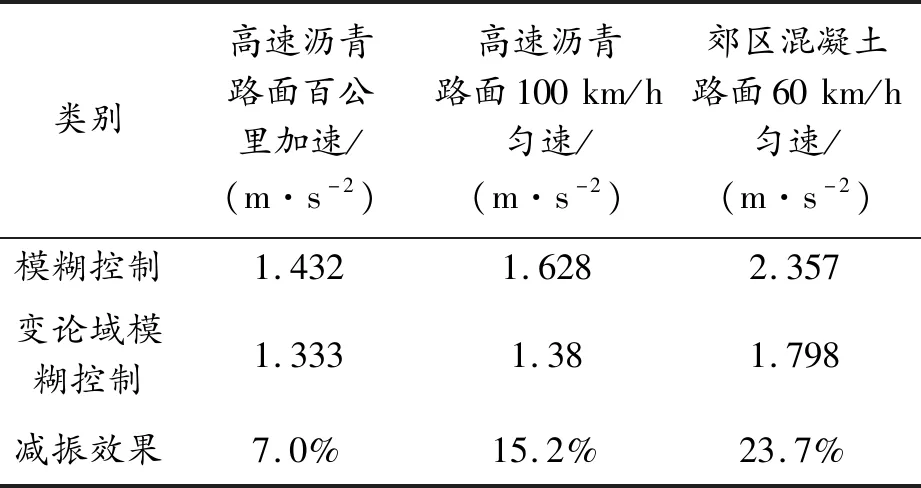
表7 车身加速度均方根值

3.1 车身加速度

由图9、表7可知，在3种路面激励下，模糊控制与变论域模糊控制的车身加速度范围大部分都在-4～6 m/s2，变论域模糊控制与模糊控制相比有所改善，其中60 km/h匀速路面激励的车身加速度下降程度最明显，达到了23.7%，100 km/h匀速和百公里加速路面激励的下降程度分别为15.2%、7.0%。

3.2 悬架动行程

由图10、表8可知，在3种路面激励下，模糊控制与变论域模糊控制的悬架动行程范围波动最大在6 mm左右，变论域模糊控制与模糊控制相比有一定恶化，但其数值变化极小，在车身姿态允许的波动范围内可忽略不计。

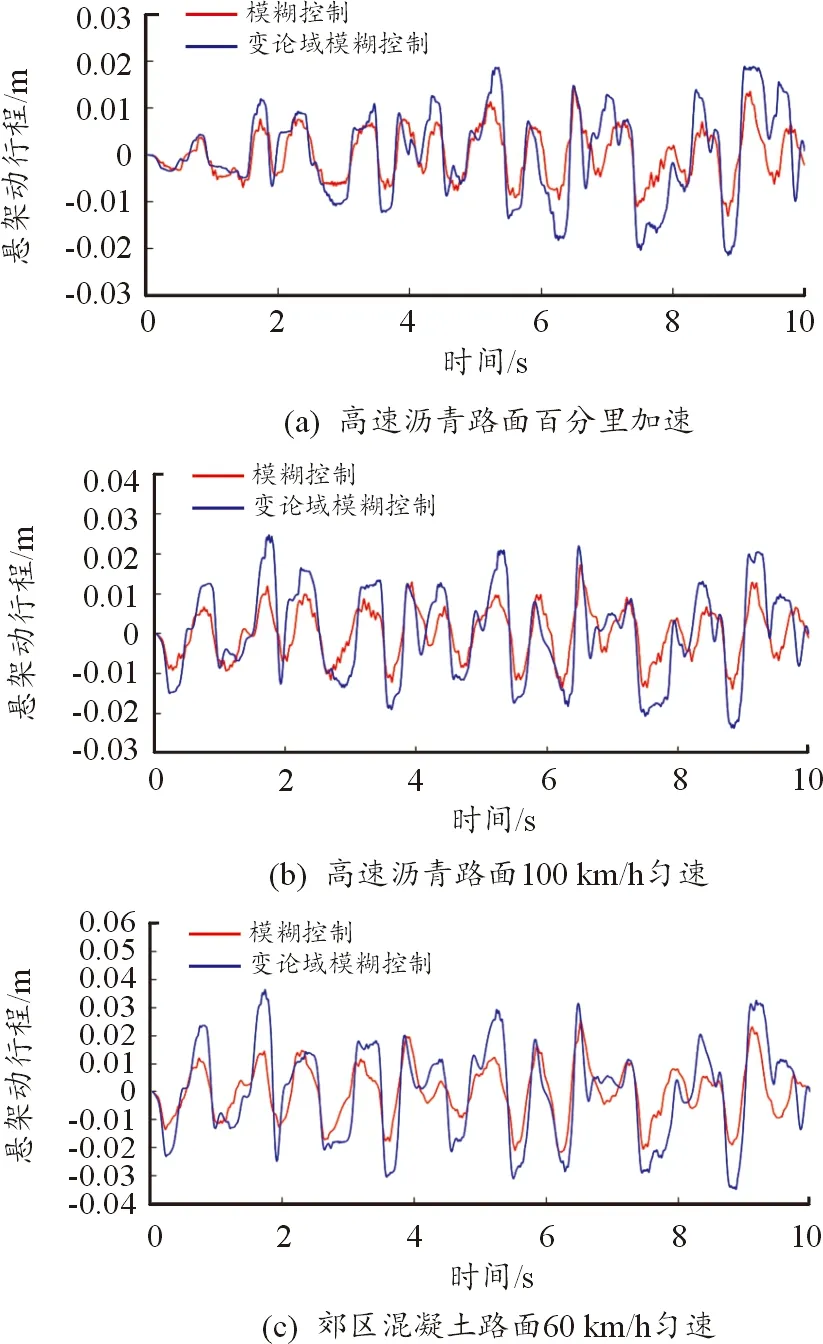
图10 悬架动行程分析

表8 悬架动行程均方根值

3.3 轮胎动载荷

由图11、表9可知，在3种路面激励下，模糊控制与变论域模糊控制的轮胎动载荷范围约由±500 N逐渐增大到±1 500 N，变论域模糊控制与模糊控制相比有较大改善，其中60 km/h匀速路面激励的轮胎动载荷下降程度达到了36.5%，100 km/h匀速和百公里加速路面激励的下降程度分别为31.2%、28.3%。

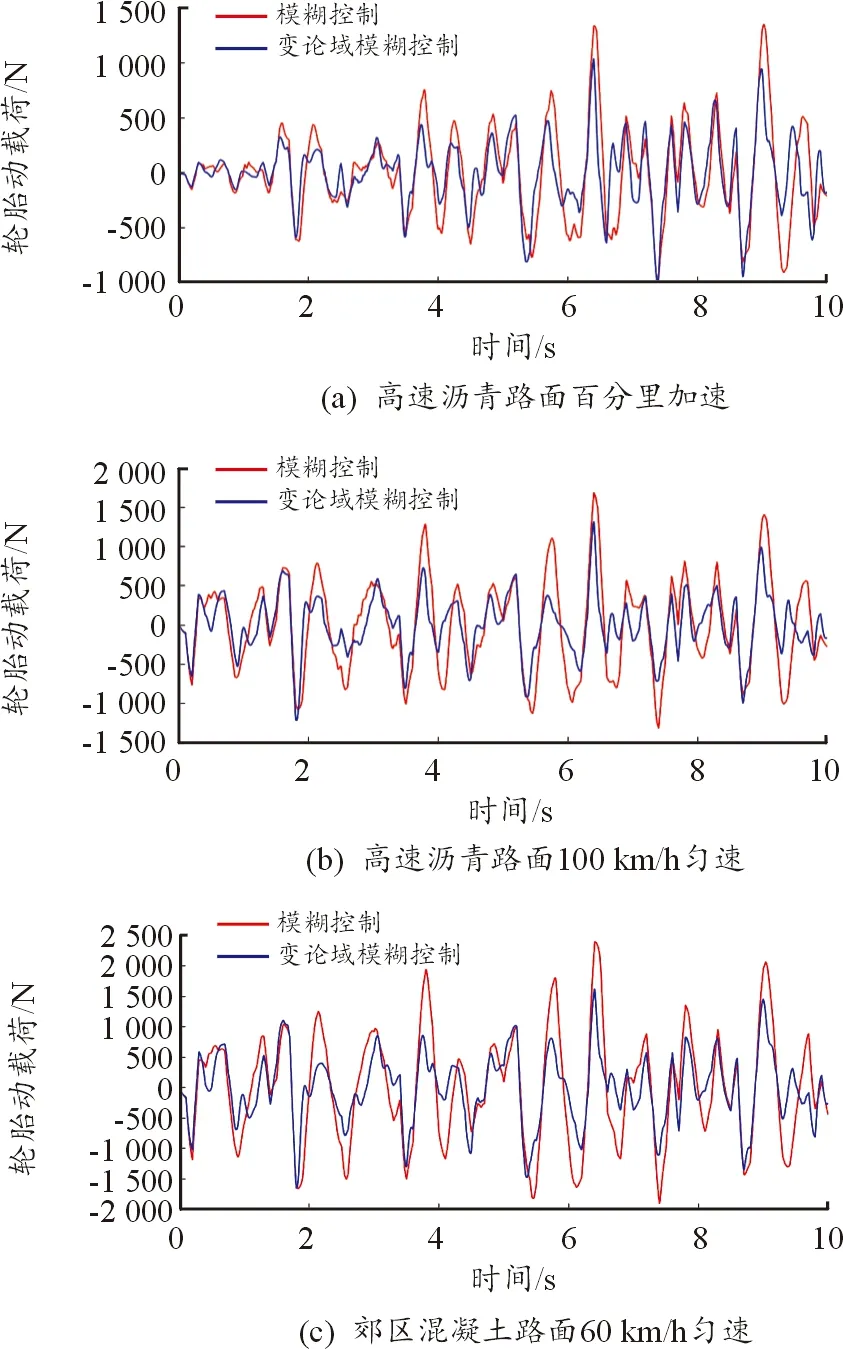
图11 轮胎动载荷分析

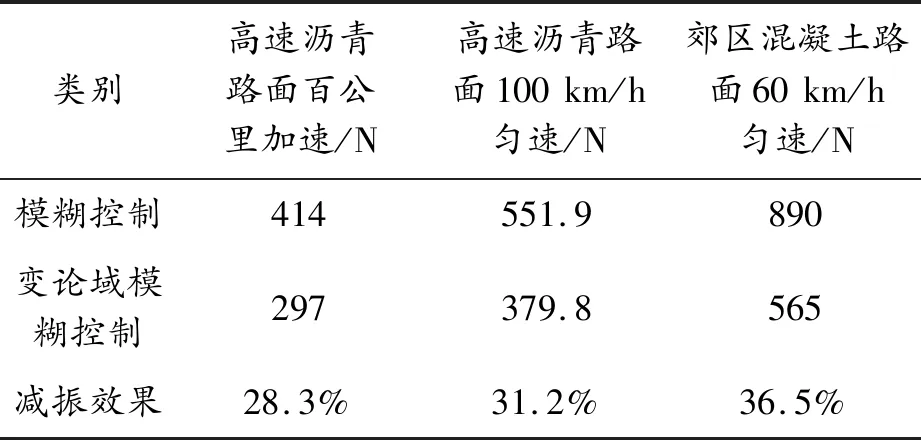
表9 轮胎动载荷均方根值

4 结论

针对高速沥青路面百公里加速、100 km/h匀速及郊区混凝土路面60 km/h匀速3种路面激励，建立了对置布置磁流变减振器1/4车辆模型，分别设计模糊控制、变论域模糊控制器对其进行控制仿真，具体有以下结论：

1)变论域模糊控制与模糊控制相比，对置布置磁流变减振器电动轮汽车的车身加速度有下降趋势，其中在60 km/h匀速路面激励下，下降程度达到了23.7%，在100 km/h匀速和百公里加速路面激励下分别为15.2%、7.0%。

2)变论域模糊控制与模糊控制相比，对置布置磁流变减振器电动轮汽车的轮胎动载荷下降趋势明显，其中在60 km/h匀速路面激励下下降程度达到了36.5%，在100 km/h匀速和百公里加速路面激励下分别为31.2%、28.3%。

3)变论域模糊控制与模糊控制相比，对置布置磁流变减振器电动轮汽车的悬架动行程有一定恶化，但波动范围小于7 mm，在允许波动范围内。