宽窄导轨上纯滚动双钢球碰撞实验

路峻岭，顾 晨，任乃敬，马泊一

(清华大学 物理系，北京 100084)

大学物理演示实验，由于装置简单、现象新奇，且可用大学物理知识进行解释，故备受大家关注，可促使学生思考，也对学生的帮助较大.本实验就是具有这些特点的实验之一.

1 实验装置及实验现象简介

本实验装置如图1所示，主要包括两条水平平行导轨，导轨宽度分别为6.5mm、23.0mm；和两个完全相同的钢球，钢球直径为25.0mm.球骑在导轨上，滚动半径分别为r=4.899mm和12.070mm.

图1 实验装置照片

本实验是要研究导轨的宽窄对碰撞实验结果的影响.实验结果是：在窄导轨上进行纯滚动双钢球碰撞实验，实验现象和滑动运动中的双钢球碰撞实验类似；而在宽导轨上进行纯滚动双钢球碰撞实验，实验现象与滑动运动中的双钢球碰撞实验明显不同，表现在能耗很大，而且都有二次碰撞发生.为什么会是这样，以下对此作具体分析.

2 碰撞过程中两钢球的受力简析以及过程阶段的划分[1-3]

碰撞过程中，两球在接触点将发生强烈的相互作用，见图2(a).设球1受到的法向冲量为I1n，切向冲量为I1t，I1t=αI1n，α为钢球之间静摩擦系数(α≈0.13)，很小，故通常I1t比I1n小得多；外力：球1与导轨接触点N1处的摩擦力冲量为Ix1=m1gα1Δt-I1tα1≈0，其中α1(α1≈0.13)为钢球与轨道之间的静摩擦系数.由于碰撞过程时间Δt极短，含时间Δt的项可被忽略，又由于I1t的作用会使球1对导轨的压力大大减小，从而摩擦力冲量Ix1被忽略.

设球2受到的法向冲量为I2n，切向冲量为I2t，I2t=αI2n，α为钢球之间静摩擦系数(α≈0.13)，很小，通常I2t比I2n小得多；外力：球2与导轨接触点N2处的摩擦力冲量为

Ix2=(m2gα2Δt+I2tα2)≈I2tα2=I2nαα2≈0

其中α2(α2≈0.13)为钢球2与轨道之间的静摩擦系数.由于碰撞过程时间Δt极短，含时间Δt的项被忽略；又有αα2<<1，故Ix2也被忽略.所以，轨道对球2的静摩擦力冲量亦被忽略.

图2 碰撞过程中两球的动量分析

由牛顿第三定律知

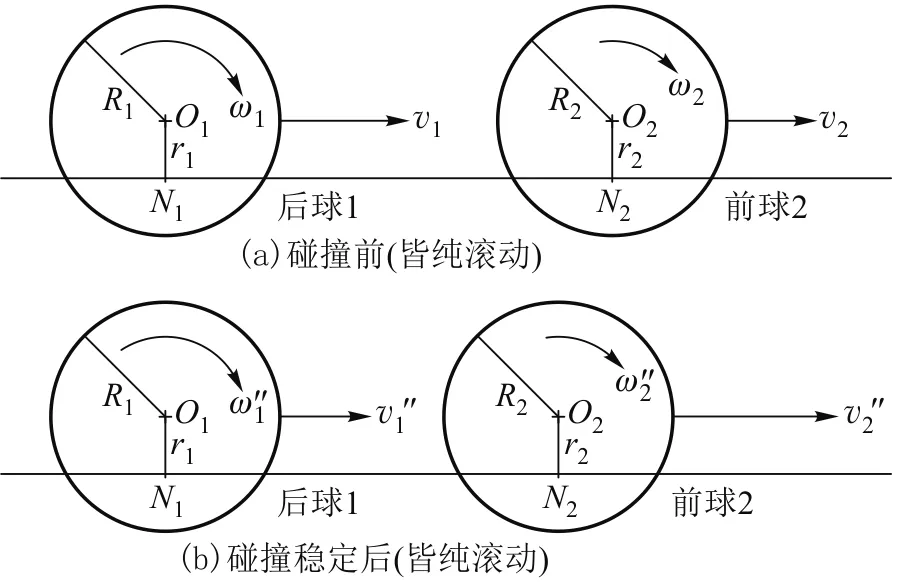
I2n=I1n=In，I2t=I1t=It<

(1)

这样，本实验所讨论的问题可以简化为纯滚动两钢球的自由碰撞问题，即完全忽略了外力(导轨摩擦力)的影响.

导轨上纯滚动双钢球的碰撞过程可分为3个阶段：1) 初始阶段，两球都在作纯滚动运动(碰撞前)；2) 碰撞过程阶段，两球在接触点的正碰(碰撞力在碰撞点与球面垂直)和切向碰撞(碰撞力在碰撞点与球面相切)同时进行，各自按照自身的动力学规律进行，因为正碰和切向碰撞遵从的规律不同，因此，在碰撞结束时刻两球的运动状态都不再是纯滚动运动；3) 自调整阶段，由于碰撞后两球不再是纯滚动状态，每一个钢球都要通过自身与导轨的相互作用变为纯滚动.下面给出各阶段的定量分析.

3 关于切向碰撞的讨论

3.1 两钢球运动状态的表示

在一个导轨上，纯滚动双球碰撞实验装置的结构如图3所示.后球(球1)和前球(球2)都在同一水平导轨上作纯滚动.

图3 碰撞前后两球的状态图示

设它们的半径相等：R1=R2=R；它们的滚动半径(由导轨的宽窄所决定)也相等，即r1=r2=r(0v2)；同时它们各自绕其过质心的水平轴转动的角速度分别为ω1、ω2.由于两钢球都是在作纯滚动，且滚动半径相等，故知ω1>ω2；约定碰撞后，它们的运动参量都用带一撇的相应的字母来表示.碰撞后钢球与导轨相互作用，自调整至再次纯滚动时，其参量都用带两撇的相应的字母来表示.即

(2)

3.2 碰撞造成两钢球的动能损耗[4，5]

根据克尼希定理，钢球的动能等于其质心平动能与绕过质心的轴的转动动能之和.故正碰和切向碰撞的能耗可以分别进行计算.球1、球2碰撞后的平动动能为

(3)

(4)

球1、球2碰撞后绕其过质心的水平轴的转动动能为

(5)

(6)

碰撞引起的动能损耗

(7)

(8)

其中，μ为折合质量，v为相对速度，j为折合转动惯量，ω为相对角速度.

正碰时，标志冲量(完全非弹性碰撞时的冲量)为μv=μ(v1-v2)，实际碰撞(非完全弹性碰撞)时的冲量In=(1+en)μv>μv，其中

(9)

为正碰恢复系数.由于两球心距有渐小至极小再离开的过程，在质心系中相对速度总是过零的，因此，0μv.

3.3 切向碰撞总是伴随碰撞[5]

(10)

为切向碰撞恢复系数.-1

4 碰撞过程分析[4，6-8]

参考图2列出碰撞过程的动力学方程.由质心运动定理(只看水平方向)

(11)

(12)

(13)

(14)

结果，质心速度为

(15)

转动角速度为

(16)

5 自调整过程

(17)

式(17)是关于FΔt、v″、ω″的三元一次方程，可解出自调节结束时钢球的运动状态和摩擦力冲量为

(18)

自调整过程的机械能损失为

(19)

这就是经历一次碰撞后球1或球2由非纯滚动变为纯滚动(自调整过程)时的机械能损失.

具体到本实验，由式(19)，分析钢球在宽窄导轨上自调整阶段的能耗，可得

(20)

可见，宽导轨时比窄导轨时自调整过程的机械能损失增大了数倍.

6 自调整过后两钢球质心速度的比较

将式(15)和式(16)，代入式(18)，可得调整过程结束时刻两球的运动状态.

球1

(21)

球2

(22)

由此可得质心的相对速度v″：

(23)

在本实验中，两个钢球完全相同，它们的转动惯量相等.最后得两球质心的相对速度为

(24)

图4 宽窄导轨上纯滚动双钢球碰撞实验中钢球速度变化

7 小结

在水平导轨上纯滚动的双钢球的碰撞，是在碰向点的正向和切向碰撞同时发生的复合碰撞，切向碰撞总是伴随碰撞.由于正碰和切向碰撞遵从不同的动力学规律，碰撞后两钢球将都不再是纯滚动状态，于是，都要通过自身与导轨的相互作用使自己变为纯滚动状态，这一过程称为自调整过程.自调整过程的能量损耗，与钢球的滚动半径和它的即时状态与纯滚动的偏离有关，宽导轨上的实验比窄导轨上的实验的能量损耗大得多，因此出现上文所列的实验现象.