最优冲量交会的研究进展

陈长青，解永春

（1.北京控制工程研究所，北京100190；2.空间智能控制技术国家级重点实验室北京100190）

最优冲量交会的研究进展

陈长青1，2，解永春1，2

（1.北京控制工程研究所，北京100190；2.空间智能控制技术国家级重点实验室北京100190）

对最优冲量交会的研究进展进行综述，介绍最优冲量交会中四类比较典型的研究成果：基于冲量校正理论的最优冲量交会、Lambert最优冲量交会、利用数值方法求解的最优冲量交会和基于邻近圆轨道交会理论的最优冲量交会，并分析这些类型的最优交会的特点。

最优冲量交会；冲量校正理论；Lambert交会；邻近圆轨道交会

1 引 言

从上世纪50年代开始，有大量的文献给出交会对接的轨迹优化设计方案。按交会时间可以分为时间不限、时间受限和固定时间这三类交会问题。对时间不限的交会的研究集中在交会对接研究的初期；时间受限的交会问题需要对燃料消耗与交会时间进行折衷；从上世纪60年代开始，交会对接中轨迹优化的研究多数集中在固定时间交会上。交会对接轨迹优化研究中的动力学方程有线性动力学方程和非线性动力学方程两大类，其中比较常用的动力学方程有CW方程、Lambert方程、T-H方程、基于圆柱坐标系的无量纲化方程和Kepler运动方程等。按推力器的形式划分有冲量交会、有限推力交会和常推力交会等。利用冲量实现交会对接的轨迹优化问题一般建立在最优控制理论的基础上，通过选择合适的冲量完成交会任务，一般称为最优冲量交会问题。

最优冲量交会问题一般写成如下的形式：

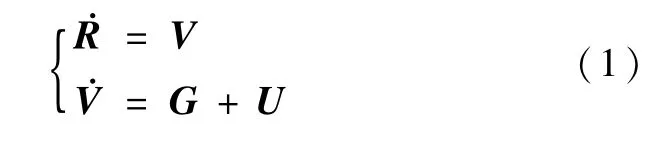
式中，R，V分别为交会中的相对位置和相对速度矢量，U为所施加控制力提供的加速度，G为中心引力差产生的加速度。在冲量制导时，第k次施加冲量用Uk表示

式中，τk为第k次冲量时对应的交会时间，ΔVk为该时刻的速度增量矢量，δ（τ-τk）为狄拉克函数。则性能指标J可以表示为

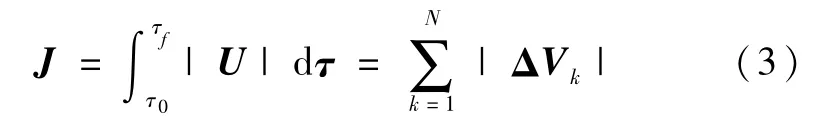
在初末相对位置和相对速度已知的情况下，这是一个典型的最优控制问题。但是即使是利用线性方程描述的交会对接过程，其最优交会解也不容易得到。1963年，Lawden基于方程（1）给出了最优冲量交会的必要条件，1968年，Lion和Handelsman在Lawden的理论基础上，提出了一种冲量校正理论，通过增加中间冲量、初始漂移、末端漂移或减少中间冲量实现对非最优轨迹的燃料优化[1]，在上述理论的基础上，不少学者对最优冲量交会问题进行了深入研究。

文献[2-6]综述交会对接轨迹优化问题，但没有文献对最优冲量交会问题进行综述，特别是按最优冲量交会的成果进行分类综述。下面介绍最优冲量交会中一些比较典型的成果，包括基于冲量校正理论的最优冲量交会、Lambert最优冲量交会、基于数值方法求解的最优冲量交会和基于邻近圆轨道交会理论的最优冲量交会。

2 最优冲量交会的研究现状

2.1 基于冲量校正理论的最优冲量交会

文献[1]把Lawden的最优冲量交会的必要条件延伸到对非最优轨迹的改进上，给出了通过校正冲量减小燃料消耗的准则，包括增加中间冲量的准则、消除某个中间冲量的准则以及是否让轨迹存在初始或末端漂移的准则，这些准则都是建立在对基向量模值分析的基础上。基向量模值随时间变化的关系有如下几种典型类型，如图1所示。

图1 基向量模值随时间变化的几种典型图形

图1中横坐标为交会时间t，纵坐标|p|为基向量的模值，虚线部分表示基向量的模值等于1，即|p|=1。其中图1（a）满足Lawden的最优冲量交会的必要条件；图1（b）在中间的某些时刻存在基向量模值大于1的情况，即在模值取最大值的时刻增加一个中间冲量可以实现燃料优化；图1（c）中，在初始的一段时间内存在基向量模值大于1的情况，通过一段初始漂移后再施加冲量的制导策略可以节省燃料；类似地在图1（d）中，施加最后一个冲量后，再自由漂移一段时间的制导策略可以减少燃料的消耗；消除某个中间冲量以实现燃料优化的冲量校正准则是建立在对一些指标函数的判断基础上的。

在文献[1]的基础上，其他学者针对直接发射交会、逃逸、“合作”交会和路径约束下的交会等实际问题，利用不同的动力学方程研究在不同交会时间和初末相对条件下的最优冲量交会问题，给出冲量解的性质和一些其他的结论。文献[7]针对非转动的球形行星上固定时间直接发射的冲量交会问题，利用冲量校正理论，研究了轨道倾角、目标航天器轨道半径和目标航天器初始相位角给定的情况下，交会时间不同时的双冲量最优交会模式与三冲量最优交会模式的燃料消耗。文献[8]讨论一类直接发射的固定时间多冲量拦截问题，目标航天器轨道为圆轨道，追踪航天器所在的行星包含转动和非转动两种类型，讨论了存在漂移的单冲量和双冲量转移策略。文献[9]在探讨固定时间邻近圆轨道平面内的冲量交会和一类受限制的非平面多冲量交会中，研究了轨道高度差和初始相位角差确定，交会时间不同时对应的最优冲量交会模式的性质，其研究成果可以应用在对交会时间和燃料消耗进行折中的救生操作和避碰机动任务上。文献[10]针对逃逸中的多冲量交会问题，利用三冲量交会策略实现了追踪航天器离开目标航天器-靠近目标航天器-制动使之与目标航天器状态一致的交会过程，利用冲量校正理论，增加中间冲量可以大大减少燃料的消耗。文献[11-12]研究了一类两个航天器都可以机动的“合作”交会问题，给出了固定时间多冲量最优交会解，仿真结果表明该交会策略比只有追踪航天器能机动的制导策略节省燃料，且大幅度扩大了交会过程中初始条件的范围，该结果可以广泛应用于对时间要求苛刻的救生任务上。文献[13-14]研究了一类存在最大最小路径约束的固定时间多冲量交会问题，利用冲量校正理论给出最优冲量交会解。文献[15]在研究一种卫星相位保持的多冲量次优控制中，考虑摄动和截断误差等对控制的影响，在求解多冲量最优解的基础上增加了中间修正冲量，仿真结果表明该制导策略具有很好的鲁棒性。

利用冲量校正理论求解最优冲量交会是一种求解最优交会问题的方法，它是建立由最优冲量交会必要条件推广所得到的冲量校正理论上的，可以应用于不同的动力学方程，由于它概念清晰，方法简单，得到广泛的应用。

2.2 Lam bert最优冲量交会

Lambert理论最初是用来解决轨道确定问题的，如图2，已知卫星在初末时刻对应的位置矢量分别为r1和r2，两个矢量之间的夹角为θ，两个位置之间的弦长为c，相隔的时间为tF-t0，利用Lambert定理可以确定卫星转移轨道的轨道半长轴，进一步还可以确定其他轨道参数。Lambert问题的求解一般用普适法[16]，近些年来还有不少文献对Lambert问题的求解进行探讨。文献[17-18]提出一种新的解超越方程的计算方法，提高Lambert问题的求解速度。文献[19]研究利用Lagrange方法求解Lambert问题的经典公式中两个中间角变量的几何特点，这两个变量与末端的半径矢量r2以及转移轨道的轨道半长轴有关。

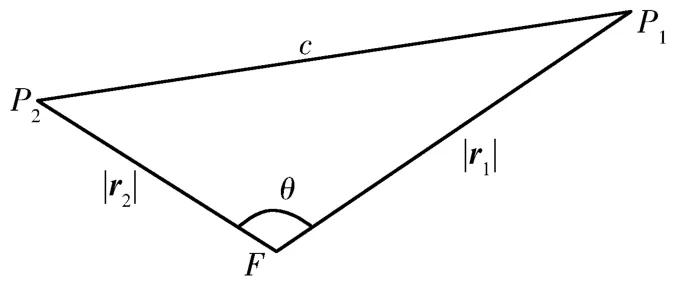
图2 Lambert问题

在交会对接研究的初期，一般利用Lambert方程描述在给定交会时间下，从追踪航天器轨道转移到目标航天器轨道的交会过程中的冲量求解问题。近些年来，Lambert交会已经成为一个独立的分支。文献[20]在研究圆轨道交会中，提出一种多圈Lambert最优双冲量交会的求解方法。其求解过程包含：（1）根据|r1|+|r2|、c和交会时间T确定满足交会要求的最大的圈数Nmax；（2）画出交会时间与半长轴的对应图形，图3为其中的一个特例，可以看到虚线表示的直线纵坐标为交会时间T，它与Nmax+1条满足交会要求的曲线存在2Nmax+1个交点，即存在2Nmax+1个转移轨道满足交会条件。在求解2Nmax+1个转移轨道的基础上，可以求得2Nmax+1个的燃料消耗ΔV；通过基向量最优交会的必要条件确定满足最优交会的解。在此基础上文献[21-22]利用ΔV与转移轨道半长轴a的关系，提出一种不需要计算2Nmax+1个转移轨道而直接获得最优双冲量交会解的方法，并应用到星座交会的制导上。文献[23]综合文献[20]和[22]的结论，把2Nmax+1个交会解以及ΔV与转移轨道半长轴a的关系画在同一个图上，通过图形可以直接得到燃料最省的多圈Lambert最优交会解。文献[24]研究航天器交会中的Lambert问题，阐述转移轨道的几何特性与转移轨道的类型，分析转移时间与转移轨道参数及变轨速度增量之间的关系。

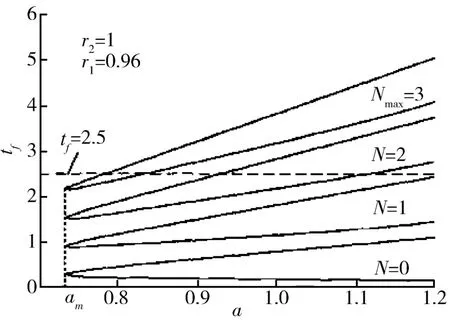
图3 多圈Lambert交会

其他研究Lambert最优冲量交会的文献有：文文献[25]针对远程导引段，提出一种满足远程导引对测控、日照、燃料和时间等各种要求的Lambert变轨方案。文献[26]在文献[25]的基础上提出新的基于普适法的多圈Lambert变轨的求解方法。文献[27]利用遗传算法研究了初始位置和转移时间不固定的Lambert双冲量轨道转移的数值解。

Lambert最优冲量交会是一种特殊的动力学方程描述的交会问题，由于Lambert方程能比较准确的描述各种交会运动，所以得到广泛的应用。近年来，以Prussing为代表的一些学者对这类制导策略进行比较深入的研究，形成了一套独立的基于多圈Lambert交会的双冲量制导理论[20-24]。

2.3 利用数值方法求解的最优冲量交会

在求解最优冲量交会时，把性能指标当作优化函数，把边界值条件和其他交会制约条件当作约束条件，则可以把最优交会化成优化问题，利用数值解法进行求解。这种方法的研究思路清晰，对于一个确定的交会问题，利用适当的优化算法很容易就可求得最优冲量解，这种求解方法可以应用于包括非线性方程在内的不同的动力学方程描述的交会问题上。文献[6]采用非直接法和直接法综述了1998年之前利用数值方法进行轨迹优化的研究成果。非直接法一般需要求解存在多个平衡点的非线性边界值问题，存在难以推导最优轨迹的必要条件、收敛域比较小和一些约束不容易描述等缺点，而直接法利用一些状态变量代替控制变量，直接利用打靶法或非线性规划等数值方法来求解。

国内也有不少学者利用数值方法研究交会对接中的轨迹优化问题。文献[28]针对冲量固定点交会中的一些具体问题，提出一种两层动态规划的优化算法，并利用这种算法，推导出使共面椭圆轨道上两个航天器在固定点交会且燃料最省的多冲量推力计算方法。文献[29-30]利用遗传算法研究CW方程描述的双冲量最优交会。文献[31]利用遗传算法研究CW方程描述的固定时间多冲量最优交会，并提出一种误差修正方法提高制导精度。文献[32]利用多阶段二维动态规划对冲量交会进行研究，得到两冲量和三冲量最优交会解。文献[27]利用遗传算法研究了初始位置和转移时间不固定的Lambert双冲量轨道转移的数值解。文献[33-34]在研究多目标最优交会中，把两个航天器的最小交会距离作为其中的一个约束目标，保证求得的轨迹是安全的。

基于数值方法求解的最优冲量交会是求解最优交会问题的一种方法，可以应用于不同动力学方程描述的最优冲量交会上，有广泛的应用前途。

2.4 基于邻近圆轨道交会理论的最优冲量交会

Prussing[35-36]的邻近圆轨道固定时间多冲量最优交会理论是上世纪60年代末轨迹优化研究中最突出的成果之一。Prussing针对于邻近圆轨道的轨道平面内的交会问题，选择两圆形轨道的中间轨道建立参考坐标系，利用线性方程下共轭变量与状态变量的解耦性，分别对基向量和边界值问题进行求解，完成了最优交会中冲量时刻、冲量方向和冲量大小的求解，可以得到四冲量、三冲量、双冲量及相应的漂移模式等几种最优交会模式，且这些模式在不同的初始条件和交会时间下有确定的分布，如图4。在此基础上部分国内外学者对其理论进行延伸。文献[37]选择平均速率参考轨道，重复了Prussing的工作，克服了中间轨道上建立参考坐标系存在的两个弊端：（1）交会结束时参考系原点与交会点没有很直观的关系；（2）对于初始相位角差比较大的交会，可能有比较大的制导误差。文献[38-39]利用四冲量最优交会模式具有的对称性，提出一种基于二次方程组计算的四冲量最优交会模式的求解方法，简化了四冲量最优交会模式的求解过程。

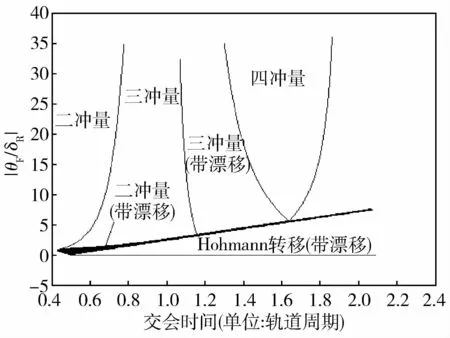
图4 最优交会模式分布图

文献[40]给出了利用线性方程描述的最优冲量交会的两个结论，即最优交会的必要条件同时满足充分条件，线性冲量最优交会中冲量的最大个数等于状态变量的个数。文献[41-42]在没有利用最优控制理论和优化理论下完成了对线性最优冲量交会中最优解存在的充分、必要条件的证明，以及最大冲量解个数等于状态变量个数结论的证明。文献[43]引入基向量的二阶导数给出最优交会新的必要条件和充分条件，该条件只需要对一些特殊点进行求解判断。

在国内也有不少学者在Prussing最优交会理论的基础上继续研究冲量最优交会。文献[44-45]在目标航天器质心建立参考系，研究CW方程下的四冲量最优交会及其应用；文献[46]选择中间参考轨道建立参考系，探讨了三冲量最优交会；文献[47]研究了CW方程下，远距离接近段中的四次、三次、二次最优冲量解作用时间和冲量幅值的求解算法。

邻近圆轨道最优交会理论是建立在最优冲量交会必要条件基础上的，由于该理论能给出在具体的初末状态和交会时间下全局的最优冲量交会模式，而且把基向量和边界值问题分开求解，其冲量求解方法概念清晰、求解方法简单，受很多学者的推崇。

2.5 最优冲量交会的一些其他问题

其他还有不少文献也研究最优冲量交会，例如探讨控制算法在最优冲量交会上的应用，利用轨道根数描述的最优冲量交会等。这些研究成果还没有比较成型的结论，离应用和推广还有一定距离。

国内对最优交会的研究一般建立在CW方程的基础上。文献[48]研究了固定时间下燃料最省的多冲量交会问题，利用拉格朗日乘子法求得燃料最省时各冲量的时间、大小及方向。文献[49]在文献[48]的基础上，适时引入当前的状态和误差信息，利用闭环控制提高制导精度。文献[50-51]研究交会对接中的双冲量最优交会问题，通过搜索合适的交会时间使得燃料得到优化。文献[52]在文献[50-51]的基础上，研究第一个冲量时刻不确定时的双冲量最优交会策略。文献[53]推导了CW方程下多冲量变轨的一般方法，并研究双冲量变轨的燃料消耗情况，提出在双冲量变轨条件下的“不可达点”及其附近的“高耗能区域”，并给出了相应的物理解释。

3 结束语

本文重点阐述了最优冲量交会中比较典型的研究成果。

（1）基于冲量校正理论的最优冲量交会和利用数值方法求解的最优交会是求解最优冲量交会问题的两种典型的方法，只要计算时间允许以及描述交会过程的动力学方程已知，利用这两种方法可以解决所有的交会问题，但是这两种方法在工程应用时，如何既迅速又准确的得到最优交会解，以及物理概念方面还需要作进一步的研究。

（2）Lambert最优冲量交会是在Lambert方程基础上发展起来的一种交会类型，目前已形成了一套独立的基于Lambert交会的两冲量交会理论，但是在三冲量、四冲量等交会问题上是否有类似的结论还有待于验证。

（3）基于邻近圆轨道的最优交会是针对两个相邻的圆轨道交会问题，能给出在不同交会时间和初末条件下最优冲量模式的分布情况，可以用来指导最优交会模式的设计。其中两冲量、四冲量交会模式由于算法简单得到了广泛的应用。但是对于带漂移的最优交会模式，目前文献中还没有给出简单、有效的求解方法。在椭圆轨道交会上，是否存在类似的分布，利用文献[35-36]的方法是否能解决问题，都还需要进行深入的研究。

[1] Lion P M，Handelsman H M.An efficient method for calculating optimal free-space n-impulse trajectories[J].AIAA Journal，1968，6（11）：2160-2165

[2] Gobetz FW，Doll JR.A survey of impulsive trajectories[J].AIAA Journal，1969，7（5），801-834

[3] Jezewski D J，Brazzel JR，Prust E E，et al.A survey of rendezvous trajectory planning[C].AAS 91-505

[4] 王旭东，潘科炎，谌颖.空间交会最优控制理论和方法的研究进展[J].航天控制，1993，11（4）：24-31

[5] 唐国金，罗亚中，张进.空间交会对接任务规划[M].科学出版社，2008

[6] Betts JT.Survey of numerical methods for trajectory optimization[J].Journal of Guidance，Control and Dynamics，1998，21（2）：193-207

[7] Gross L R，Prussing J E.Optimal multiple-impulse direct ascent fixed-time rendezvous[J].AIAA Journal，1974，12（7）：885-889

[8] Prussing J E，Eellnitz L J，Hecka thorn W G.Optimal impulsive time-fixed direct-ascent interception[J].Journal of Guidance，Control and Dynam ics，1989，12（4）：487-494

[9] Prussing J E，Chiu J H.Optimal multiple-impulse time fixed rendezvous between circular orbits[J].Journal of Guidance，Control and Dynamics，1986，9（1）：17-22

[10] Prussing J E，Clifton R S.Optimal multiple-impulse satellite evasive maneuvers[J].Journal of Guidance，Control and Dynamics，1994，17（3）：599-606

[11] Prussing JE，Conway B A.Optimal terminal maneuver for a cooperative impulsive rendezvous[J].Journal of Guidance，Control and Dynamics，1989，12（3）：433-435

[12] Mirfakhraie K，Conway B A.Optimal cooperative time fixed impulsive rendezvous[J].Journal of Guidance，Control and Dynam ics，1994，17（3）：607-613

[13] Taur D R，Carroll V C，Prussing J E.Optimal impulsive time-fixed orbital rendezvous and interception with path constraints[J].Journal of Guidance，Control and Dynamics，1995，18（1）：54-60

[14] Taur D R.Optimal，impulsive，time-fixed orbital rendezvous and interception with path constraints[D].PhD Thesis，Dept.of Aeronautical and Astronautical Engineering of University of Illionis，1989

[15] 白鹤峰，任萱.卫星相位保持的多冲量次优控制[J].航天控制，1999，17（3）：6-12

[16] Bate R R著，吴鹤鸣，李肇杰译.航天动力学基础[M].北京航空航天大学出版社，1990

[17] Battin R H.Lambert's Problem Revisited[J].AIAA Journal，1977，15（5）：707-713

[18] Battin R H，Vaughan R M.An elegant Lambert algorithm[J].Journal of Guidance and Control，1984，7（6）：662-670

[19] Prussing J E.Geometrical interpretation of the angleα andβin Lambert's problem[J].Journal of Guidance and Control，1979，2（5）：442-443

[20] Prussing JE.A class of optimal two-impulse rendezvous using multiple-revolution Lambert solutions[J].The Journal of the Astronautical Sciences，2000，46（2）：131-148

[21] Shen H J，Tsiotras P.Optimal two-impulse rendezvous between two circular ortits using multiple-revolution Lambert's solutions[C].AAS/AIAA Astrodynamics Specialist Conference，Aug.16-18，1999

[22] Shen H J，Tsiotras P.Optimal two-impulse rendezvous usingmultiple-revolution Lambert solutions[J].Journal of Guidance，Control，and Dynamics，2003，26（1）：50-61

[23] 朱仁璋，蒙薇.航天器交会两点边界值问题[J].宇航学报，2006，27（6）：1182-1186

[24] 朱仁璋，蒙薇，胡锡婷.航天器交会中的Lambert问题[J].中国空间科学技术，2006，26（6）：49-55

[25] 韩潮，段彬，付红勋.远程导引可行飞行方案寻求算法研究[J].中国空间科学技术，2002，22（1）：47-52

[26] 韩潮，谢华伟.空间交会中多圈Lambert变轨算法研究[J].中国空间科学技术，2004，24（5）：9-14

[27] 陈统，徐世杰.基于遗传算法的最优Lambert双冲量转移[J]北京航空航天大学学报，2007，33（3）：273-277

[28] 谌颖，黄文虎，倪茂林，王旭东，白拜尔.多冲量最优交会的动态规划方法[J].宇航学报，1993，14（2）：1-7

[29] 王华，唐国金.用遗传算法求解双冲量最优交会问题[J].中国空间科学技术，2003，23（1）：26-30

[30] 王华，唐国金.遗传算法在航天器最优交会中的应用研究[J].航天控制，2003，21（1）：16-21

[31] 李晨光，肖业伦.多冲量C-W交会的优化方法[J].宇航学报，2006，27（2）：172-176

[32] 刘鲁华，汤国建，余梦伦.利用动态规划原理实现多冲量最优交会问题[J].国防科技大学学报，2006，28（6）：38-42

[33] Luo Y Z，Tang G J，Lei Y J.Optimal multi-objective linearized impulsive rendezvous[J].Journal of Guidance，Control，and Dynamics，2007，30（2）：383-389

[34] Luo Y Z，Lei Y J，Tang G J.Optimal Multi-objective nonlinear impulsive rendezvous[J].Journal of Guidance，Control，and Dynamics，2007，30（4）：994-1002

[35] Prussing J E.Optimal four-impulse fixed-time rendezvous in the vicinity of a circular orbit[J].AIAA Journal，1969，7（5）：928-935

[36] Prussing JE.Optimal two and three-impulse fixed-time rendezvous in the vicinity of a circular orbit[J].AIAA Journal，1970，8（7）：293-310

[37] Frank C L，Plexico L D.Improved solution of optimal impulsive fixed-time rendezvous[J].Journal of Spacecraft and Rocket，1982，19（6）：521-528

[38] Carter T E，A lvarez S A.Four-impulse rendezvous near circular orbit[C].AIAA/AAS，Astrodynamics Specialist Conference and Exhibit，Boston，MA，Aug.10-12，1998

[39] Carter T E，Alvarez SA.Quadratic-base computation of four-impulse optimal rendezvous near circular orbit[J].Journal of Guidance，Control and Dynam ics，2000，23（1）：109-117

[40] Prussing J E.Optimal impulsive linear systems：sufficient conditions and maximum number of impulses[J].The Journal of the Astronautical Science，1995，43（2）：195-206

[41] Carter T E，Hull D G.Optimal impulse space trajectories based on linear equations[J].Journal of Optimization and Application，1991，70（2）：277-297

[42] Carter T E，Hull D G.Linearized impulse rendezvous problem[J].Journal of Optimization Theory and Applications，1995，86（3）：553-584

[43] Carter T E.Necessary and sufficient conditions for optimal impulsive rendezvous with linear equations of motion[J].Dynamics and Control，2000，No.10：219-227

[44] 陈新海，陈文胜.航天器四冲量固定时间最优交会[J].宇航学报，1994，15（2）：71-79，110

[45] 雷勇，汤国建，王旭东.联盟TM交会对接的地面远程导引段制导方法分析和研究[J].航天控制，1999，17（4）：51-57

[46] 齐映红，曹喜滨.三冲量最优交会问题的解法[J].吉林大学学报（工业版），2007，36（4）：608-612

[47] 许伦辉，徐建闽.交会对接远距离接近段制导研究[J].飞行力学，1998，16（2）：90-96

[48] 谌颖，王旭东.多冲量最优交会[J].航天控制，1992，10（1）：25-32

[49] 张小伟，李英波.空间交会中拉格朗日乘子法的工程应用[J].上海航天，2007，24（4）：30-33，47

[50] 林来兴，王立新.空间交会对接双冲量最优控制[J].中国空间科学技术，1995，15（6）：28-34

[51] 林来兴，王立新.空间交会对接的双冲量最优控制[J].航天控制，1996，14（1）：12-18

[52] 荆武兴，耿云海，杨旭，吴瑶华.空间交会寻的最优轨道机动[J].中国空间科学技术，1998，18（2）：22-27

[53] 向开恒，肖业伦.空间交会中冲量变轨燃料消耗研究[J].中国空间科学技术，1999，19（3）：9-15，50

Development of Optimal Impulsive Rendezvous

CHEN Changqing，XIE Yongchun
（1.Beijing Institute of Control Engineering，Beijing 100190，China；2.National Laboratory of Space Intelligent Control，Beijing 100190，China）

The development of optimal impulse rendezvous is reviewed in this paper.The optimal impulse rendezvous based on the criterion of impulse modifying，Lambert optimal rendezvous，the optimal impulse rendezvous solved by numerical methods and the optimal impulse rendezvous based on the theory of optimal rendezvous between neighboring circular orbits are introduced.And then the characters of these optimal impulse rendezvous are analyzed.

optimal rendezvous；criterion of impulse modifying；Lambert rendezvous；optimal rendezvous between neighboring circular orbits

V526

A

1674-1579（2008）06-0018-06

*国家自然科学基金资助项目（90305024）.

2008-08-12

陈长青（1979-），男，福建人，博士研究生，研究方向为交会对接的制导技术（e-mail：changqingchen@hotmail.com）。