嫦娥一号卫星地月转移轨道中途修正分析

杨维廉，周文艳

（中国空间技术研究院总体部，北京100086）

嫦娥一号卫星地月转移轨道中途修正分析

杨维廉，周文艳

（中国空间技术研究院总体部，北京100086）

中国第一颗月球探测卫星“嫦娥一号”于2007年10月24日成功发射并于11月7日顺利进入了距月面200km的科学探测的使命轨道，原计划在整个飞行过程中比较关键的轨道段是地月转移轨道段。要进行2至3次中途轨道修正，而实际的飞行结果只在第41小时作了一次很小的修正，所用的速度增量是4.8m/s。基于有关的实测数据对此进行详细的分析，以期获得一些规律性的认识。

月球探测；月球卫星；调相轨道；地月转移轨道；中途修正机动

1 引 言

2007年10月24日，中国第一颗月球探测卫星“嫦娥一号”成功发射，经过14天的飞行于11月7日进入了距月面200km的科学探测使命轨道。整个飞行轨道主要包括3个部分：调相轨道、地月转移轨道和环月飞行的使命轨道。长征三号甲火箭将卫星送入周期约16h的超地球同步轨道运行3圈后，在近地点进行第一次轨道机动将轨道周期变成24h，再运行3圈后在近地点作第二次近地点机动进入48h周期的轨道，在这条轨道上再次运行到近地点后完成了调相轨道段飞行，为了飞向月球还需作第三次近地点轨道机动才能进入到关键的地月转移轨道。为了消除进入这条轨道时的初始误差，一般都需要在中途进行轨道修正。对于不采用调相轨道而直接飞达月球的直接转移方式，一般都需要进行两次中途修正，第一次是在飞行的最初一天时间内，第二次是在到达月球前的一天时间内[1]。

嫦娥一号卫星的转移轨道飞行时间是114h，中途修正的设计是：第一次修正在第17小时进行，最后一次是在到达前24h，即第90h进行，此外在第41小时安排一次备选的修正，在第一次修正后的剩余误差超过特定的上界时执行。

嫦娥一号卫星实际飞行十分理想，只在飞行的第41小时作了唯一的一次中途修正，所用的速度增量只有4.8m/s。本文基于有关的实测数据对此进行详细的分析，以期获得一些规律性的认识。

2 轨道控制误差及其对轨道的影响

嫦娥一号卫星在完成48h的调相轨道运行进入转移轨道近地点时需进行一次大的轨道机动，使近地点速度增加到10.599km/s，所需的速度增量是0.199km/s。这个速度增量的误差将引起不期望的近地点轨道误差。

轨控误差是指轨道机动时实际产生的速度增量v→与要求的速度增量v→0之差Δv→。为了分析这项误差对轨道的具体影响，需要用到以加速度3分量表示的轨道摄动方程[2]：

式中，R，T，W是摄动加速度沿径向、横向和法向的3个分量，其余的参数都是轨道的有关参数：a，e，i，Ω，ω，f是6个开普勒根数，n是平均运动，即平均角速度，p=a（1-e2）是半通径，r是卫星的地心距，E是偏近点角，u=ω+f是纬度幅角。

可以把速度增量误差看成是脉冲，并分解成相应的3个分量ΔvR，ΔvT，ΔvW，于是式（1）变成

对于近地点的轨道机动，式（2）可以简化为

为了进行具体的估算需要用到表1给出的地月转移轨道的标称值。

表1 地月转移轨道标称值

把轨道根数代入式（3）后得到便于估算的简化公式

式中，速度单位是km/s，角度单位是（°）。

3 中途修正速度增量与近地点轨道误差的关系

地月转移轨道中途修正并不是把轨道修正为标称轨道，这是不可能的。中途修正只能是在有误差的位置上施加一个合适的速度增量，使卫星沿着一条新的转移轨道来满足初始的要求。中途修正所要修正的误差是由进入转移轨道近地点时的误差引起的，而这个误差主要是进入转移轨道所施加的速度增量的误差和运载与卫星分离时的误差。

文献[3]提供了计算中途修正速度增量与转移轨道近地点的误差关系的方法。对于所采用的求解转移轨道的数学模型，所要考虑的近地点误差是近地点速度vp，升交点赤经ΔΩ，近地点幅角ω和轨道倾角i的误差。它们之间的微分关系是：

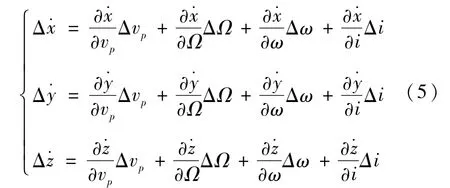
式中的12个误差传递系数可以用数值方法近似地求出。

下面分别给出在17h、41h和90h进行中途修正时这些传递系数的具体数值。表中速度的单位是m/s，角度的单位是（°）。

表2 17h中途修正的误差传递系数

表3 41 h中途修正的误差传递系数

表4 90h中途修正的误差传递系数

4 近地点轨道误差的影响

进入转移轨道近地点以前的轨道误差是由运载所提供的发射轨道误差以及卫星在调相轨道运行过程中的几次机动误差组成，在作最后一次近地点机动前可以根据实测的结果重新计算地月转移轨道参数的标称值，把近地点高度和轨道倾角的实测值作为标称值计算所需的近地点机动的速度增量，因此可以不再考虑倾角误差对中途修正的影响。

4.1 发射窗口误差的影响

运载所提供的发射轨道的升交点赤经Ω将随着发射时刻的变化而变化，发射窗口的前沿对应于设计轨道所要求的升交点赤经。发射时刻每延后4min，轨道的升交点赤经将增加1°的误差。嫦娥一号卫星的窗口为35m in，由此可能产生的升交点赤经的最大误差是8.75°。如果这种情况发生，根据表2～4很容易计算出17h、41h和90h修正所需的速度增量分别是236m/s、268m/s和807m/s。嫦娥一号卫星几乎是零窗口发射，这部分误差完全可以忽略。

4.2 轨控误差的影响

地月转移轨道的近地点机动所需的速度增量为199m/s，因此要求满足|Δv→i|≤4m/s。需要注意的是同样大小的误差由于各个分量的不同，其影响会有很大的差别。表5给出3种极端情况。

把这些数据代入表3可以得到41h中途修正所需的速度增量，见表6。

表5 近地点轨道机动误差的3种极端情况对轨道的影响

从表6可以很明显看出，横向，即近地点速度方向的误差对中途修正的速度增量起了决定性的作用，而其它两个方向的误差几乎可以忽略，这是近地点机动的重要特点。

表6 3种极端情况的中途修正速度增量

4.3 基于实测数据的分析

嫦娥一号卫星进行地月转移轨道近地点机动的标称时刻是北京时间2007年10月31日17时25分28秒，实际执行的时间与这个时刻相差很小。轨道机动后经过若干次测轨给出的对应历元为17时28分39秒的轨道根数，见表7。

表7 实测的转移轨道根数

因为这不是近地点，我们用精确的模型将其推算到近地点，对应的时刻是17时25分0秒，比标称历元早28s，对应的轨道根数见表8。

表8 推算的近地点轨道根数

由此进一步算出近地点高度是614.427km，近地点速度是10.58825km/s。这是有误差的轨道，只需解算出对应的、符合要求的标称轨道便可算出它的误差，它的相应的3个参数结果是：vp=10.58836km/s，Ω=168.501°，ω=185.428°；其误差是Δvp=-011m/s，ΔΩ=-0.261°，Δω=0.274°。要说明的是这里的标称轨道已经不是设计的标称轨道，而是根据新的近地点高度和轨道倾角解算出来的新的标称轨道。因此倾角的变化量30.877°-31°=-0.123°不构成误差，倾角的测定误差非常小，不需要考虑它的影响。

现在基于这个误差计算41h进行中途修正所需的速度增量。先用综合的方法来算，其结果是

这与嫦娥一号卫星实际的中途修正的结果非常符合。还可以用第二节中的方法来分别估算，这样可以看出3个主要误差源各自的贡献。Δvp=-0.11m/s的贡献是

ΔΩ=-0.261°的贡献是

Δω=0.274°的贡献是

3项之和是

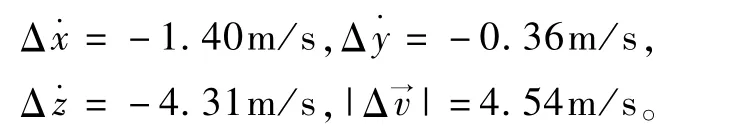
两种分析方法的结果几乎一样。

基于这两种估算的结果可以有把握地说，沿近地点速度方向上的分量vT的误差很小，是0.11m/s，相对误差是万分之五。除此以外还发现升交点赤经Ω的误差与近地点幅角ω的误差会出现相互抵消的可能。

轨道机动的另两个速度误差分量只能通过本次机动所产生的ΔΩ，Δω和Δi来推算，为此基于机动前的48h轨道的最后一组（北京时间2007年10月31日8时0分0秒）实测数据，采用精确的模型来推算机动时刻的相应轨道的轨道根数，其结果是：

i=30.882°，ω=185.986°，Ω=168.223°。

在最后一次近地点机动后测得的相应轨道根数除表7列出的一组数据外，还有另一组不同的数据。这两组不同的数据对于分析中途修正结果基本无差别，但对于分析机动后的速度增量的误差会有较大的不同，需要认真鉴别，参见表8～9。

表9 两组不同的实测结果

由此算出机动后的变化是

表10 两组不同的变化

表10中给出的近地点幅角的变化量Δω明显地比其他两个量大得多，与运载的入轨误差是同样量级，这显然不是控制的误差，而是根据轨控策略要求人为实现的，这样做是为了抵消ΔΩ的影响。倾角和升交点赤经的变化量Δi，ΔΩ基本上是由控制结果的法向误差ΔvW引起的，但两组的ΔΩ有很大的差别。考虑到倾角对这项误差比升交点赤经更敏感，而且根据两组实测值算出的结果应该基本一致，据此，用倾角的变化量Δi来推算法向误差ΔvW更可信。采用Δi=-0.007°，根据表5可以算出ΔvW=-1.3m/s，这个误差分量与总的速度增量199m/s之比是0.65%，即6.5‰。速度增量的径向分量的误差ΔvR只能通过Δω来推断，而所获得的变化量Δω=-0.248°主要是人为控制的结果，控制的误差部分无法分离出来。不过认为它与法向误差ΔvW为同一量级应该是合理的。据此判断这次重要的近地点机动的轨控相对误差约为9‰。

利用中途修正过程的实测结果来推断控制误差更为简单且清楚，因为中途修正是直接解算所需的3个速度增量的分量。41h中途修正所需的4.8m/s速度增量是根据对这一时刻的轨道进行的预测以及到达近月点的轨道参数的标称值计算的，要分辨这次中途修正的误差比较容易，只要用同样的方法基于修正后的轨道以及到达近月点的轨道参数的标称值再计算一次所需的速度增量就可以。计算的结果是：

这个误差除了控制误差外还包含测轨误差，但测轨误差实际上是非常小的。比较了中途修正后测定的同一时刻的6组不同的轨道根数，其中半长轴彼此差别不超过3km，据此可以推算出速度误差是0.0072m/s，因此0.21m/s基本上是轨道控制误差。将这个误差除以4.8m/s的速度增量，得到相对误差是4.4%，即这个唯一的一次中途修正的轨道控制误差为4.4%。

5 结 论

嫦娥一号卫星飞行过程在地月转移轨道的表现令人非常满意，它只需在飞行41h后进行一次轨道修正而且所需速度增量不到5m/s，这已成为嫦娥工程的一个很大亮点。哪些因素导致了这个结果，是偶然还是有其必然性。对此进行实事求是的分析十分必要。基于本文的分析似乎可以得出如下的一些结论：

1）长征三号甲的零窗口的发射是最根本的原因。嫦娥一号卫星的轨道设计方案设定的发射窗口的大小是35m in，为此分配的速度增量为240m/s，相应的燃料需求约150kg。零窗口的实现不仅使这些需求都变成了零，而且使实际的转移轨道有可能与标称的转移轨道相当接近。

2）运载将卫星送入轨道时的角度随机误差ΔΩ与Δω的量级是零点几度，这样量级的误差不会给中途修正增加很大的负担，但在进入地月转移轨道的最后一次近地点机动前可以充分利用两者相互抵消的可能性在增加近地点速度的同时来改变近地点幅角ω。

3）调相轨道的采用使得进入地月转移轨道所需的速度增量大大地减小，于是可以按比例地减小速度增量的误差。为了加大这个效果应该尽可能使前一圈调相轨道的周期更长，例如将48h的轨道改为72h的轨道。

4）表5和表6的结果清楚地说明，转移轨道近地点机动时沿近地点速度方向分量的误差是至关重要的，而另两个分量的影响是次要的。这个结论也适用于调相轨道飞行过程的所有近地点机动，因为轨道周期的精度仅决定于近地点速度的精度。嫦娥一号卫星调相轨道所包含的16h、24h和48h轨道的周期都相当精确的原因就在于此。嫦娥一号卫星在轨道机动的控制中采用了精度可达万分之几的加速度计，这是实现近地点速度方向分量的精确控制的最根本原因。

[1] 杨维廉，周文艳.嫦娥一号卫星轨道设计[J].航天器工程，2007，16（8）：16-24

[2] Chobotov V A.Orbital mechanics[M].3rdedition.American Institute of Aeronautics and Astronautics，Inc.，2002

[3] 周文艳，杨维廉.月球探测器转移轨道的中途修正[J].宇航学报，2004，25（1）：89-92

Analysis on Midcourse Correction of Translunar Trajectory for CE-l

YANGWeilian，ZHOU Wenyan
（Beijing Institute of Spacecraft System Engineering，CAST，Beijing 100086，China）

CE-1，the Chinese first lunar exploration satellite，was successfully launched on 24 Oct.2007 and captured in to a mission orbit of 200 km from lunar surface on 7 Nov.2007.The translunar trajectory is the key section within the whole flight process.According to the original design 2 or 3 times of midcourse corrections would be performed during this orbital segment.However，only one correction maneuver has been carried out at the 41st hour after the translunar trajectory insertion and the velocity increment needed was only 4.8m/s.Some detailed analysis based on the real tracking data and the orbit determination results is presented here in this paper.

lunar exploration；lunar satellite；phasing orbit；translunar trajectory；midcourse correction maneuver

V 448.2

A

1674-1579（2008）06-0003-05

2008-07-24

杨维廉（1941-），男，浙江人，研究员，博士生导师，研究方向为轨道力学和航天使命分析与设计（e-mail：yangw l@cast.cn）。