基于近似模型的后背门轻量化优化

王路展,张瑞乾，2,陈 勇，2

(1.北京信息科技大学 机电工程学院，北京 100192；2.北京信息科技大学 北京电动车辆协同创新中心,北京 100192)

0 引言

汽车行业正朝着智能、安全、节能、环保的方向发展[1]。汽车轻量化是降低汽车能耗、减少排放的最有效措施之一，汽车每减重100 kg，每百公里就可减少燃油消耗0.3～0.5 L、CO2排放可减少8～11 g[2]。而汽车后背门是汽车上重要的开闭件且尺寸较大，行车时不能出现振动、变形，这就要求后背门具有较高的刚度、合适的模态频率及最优的质量[3-4]。戚振杰等[5]通过OptiStruct中的尺寸优化和材料替换的方式对汽车后背门进行优化，不同程度地改善了其刚度和模态。邢志波等[3]通过拉丁超立方实验设计及Kriging代理模型进行质量优化；朱茂桃等[6]基于6σ稳健性的车门多学科优化设计方法对车门进行优化。李军等[7]基于HyperStudy中的部分因子试验设计选择关键钣金件厚度进行优化设计。刘豪等[8]针对某SUV车型后背门的一阶模态频率较低，运用多学科优化方法，在后背门质量增加较小的情况下，使得后背门的一阶固有频率得到了提高。Morteza Kiani等[9]对白车身运用多学科优化并同时考虑材料的替换，使其在实现轻量化的同时又满足碰撞安全标准。

本文在对某车型汽车的后背门进行静力学及模态分析的基础上，用HyperStudy对其进行多学科优化。

1 后背门有限元模型的建立

后背门是由不同的钣金薄板冲压焊接而成，因此采用壳单元进行离散。目标网格的大小设为8 mm，焊点用ACM单元进行模拟，胶粘采用adhesives连接单元模拟，螺栓孔用RBE2单元连接。最终汽车后背门有限元模型如图1所示。其材料的属性参数如表1所示。后背门有限元模型中壳单元的个数为35 494个，其中包含33 606个四边形单元及1 888个三角形单元，三角形单元比例为5.32%，小于企业建模要求的上限8%，共有58个焊点。后背门的质量为11.23 kg。

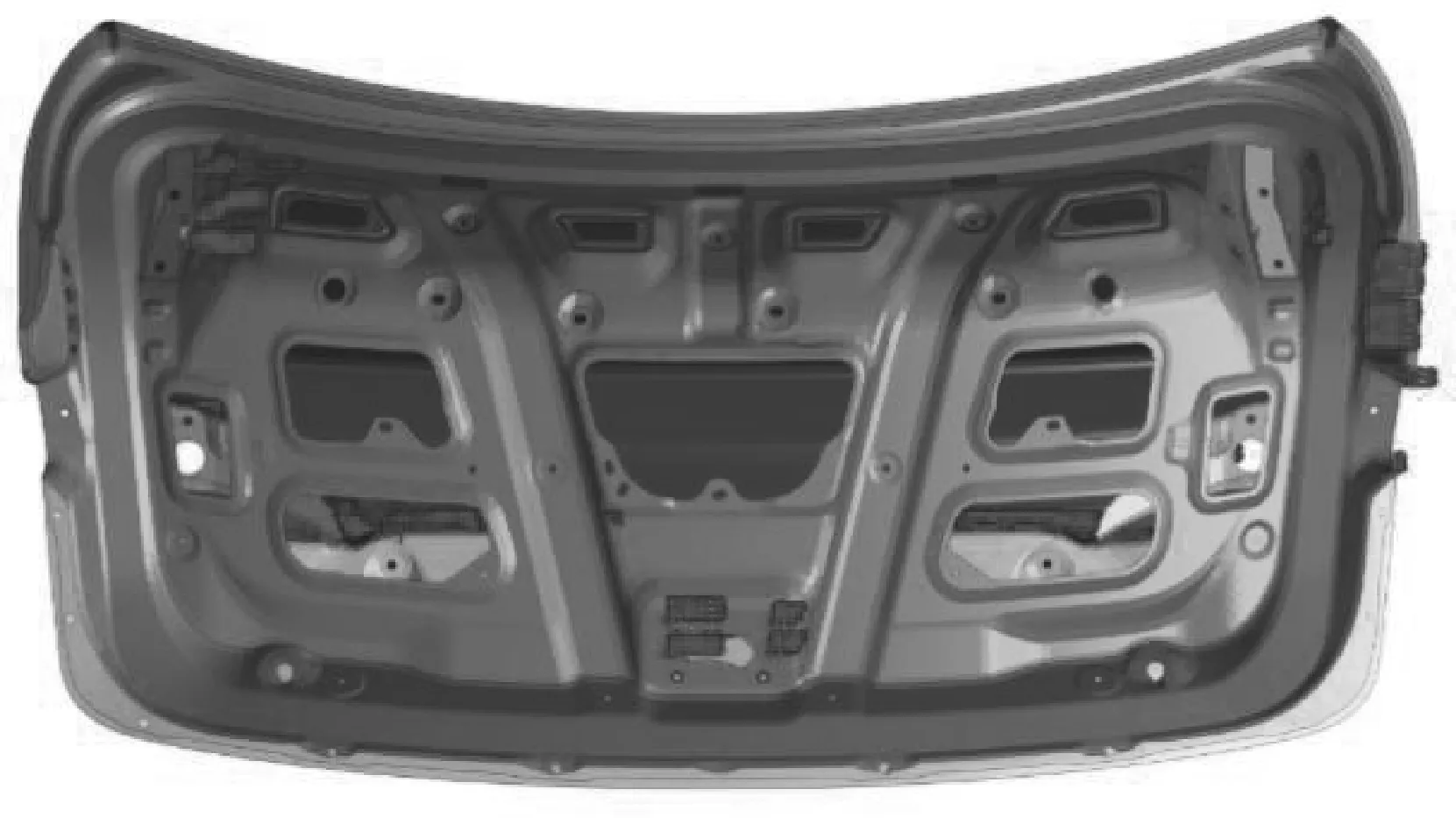
图1 后背门有限元模型

表1 材料属性参数

2 后背门模态与刚度分析

2.1 模态分析

后背门模态与车身性能有着很大的关系，当其模态频率与白车身模态频率接近时很有可能产生共振[10]。用OptiStruct求解器求取前10阶的模态振型，前6阶为刚性运动，其模态频率接近于零，从第7阶开始为一阶扭转模态，第8阶为一阶弯曲模态，如图2～3所示。

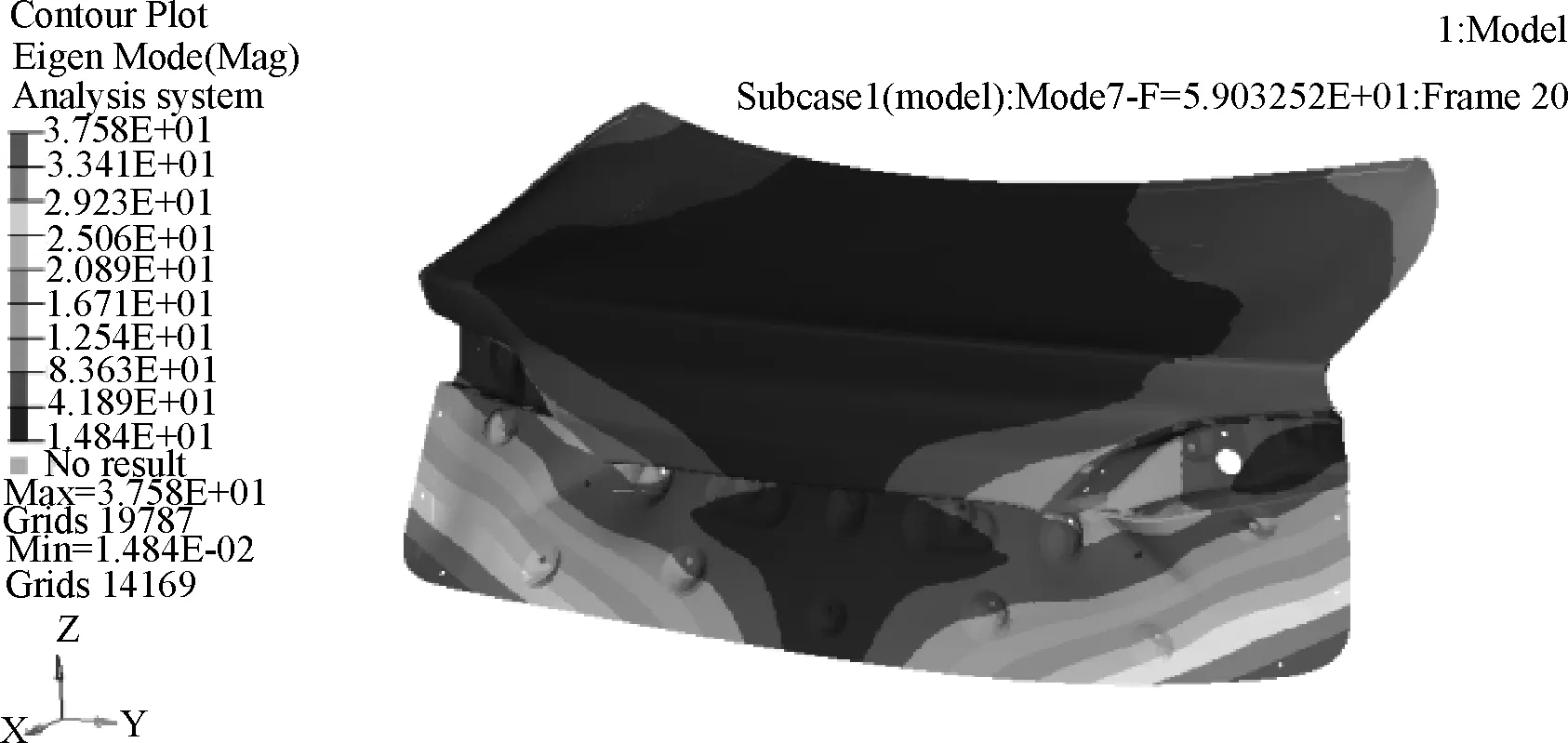
图2 一阶扭转模态

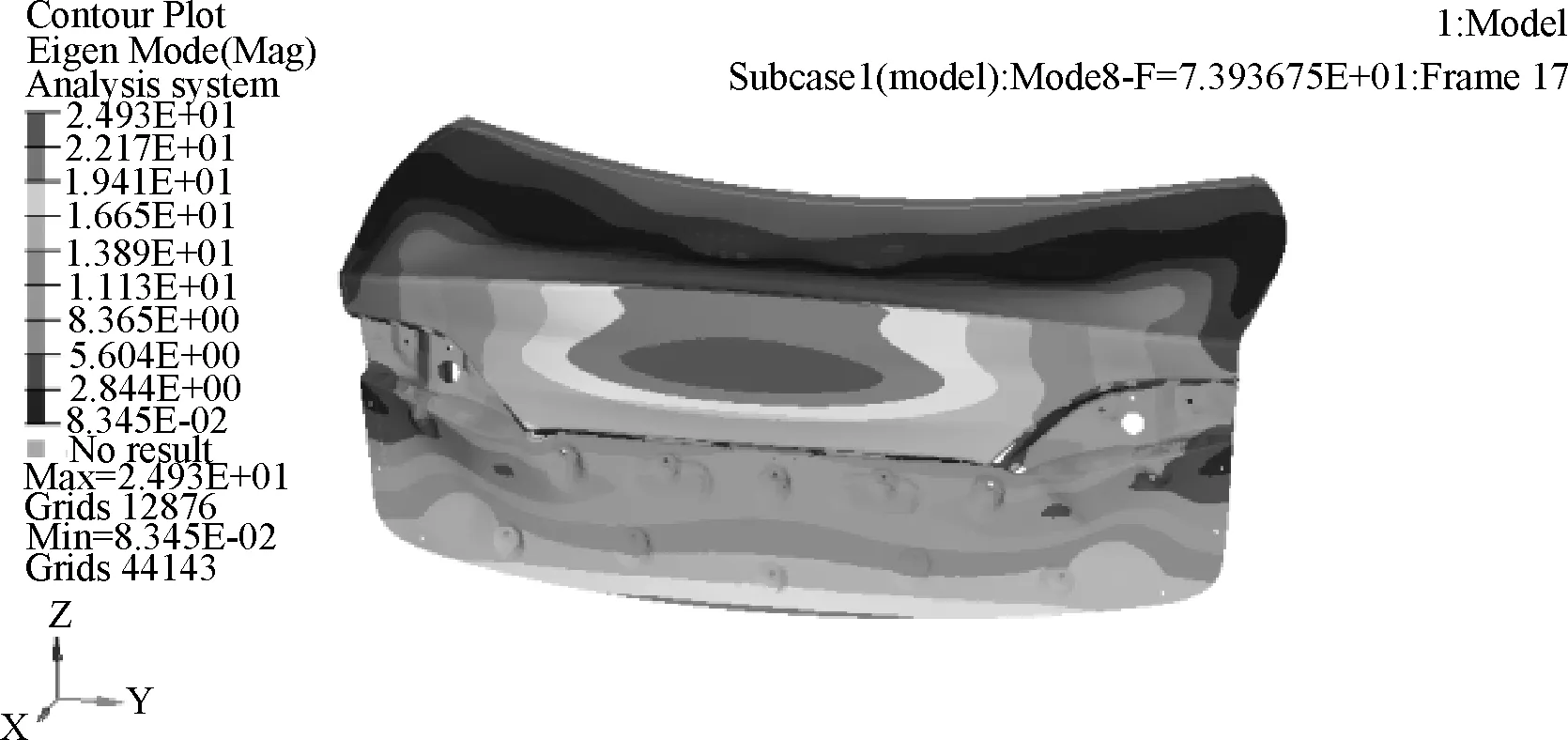
图3 一阶弯曲模态

从图中可以看出：后背门一阶扭转频率为59.03 Hz，大于企业目标值40 Hz；一阶弯曲模态频率为73.93 Hz，大于企业目标值45 Hz。由此可知该车型后背门的模态性能满足企业要求，且有富余。

2.2 刚度分析

参照文献[5]对后背门所采取的扭转刚度与弯曲刚度的仿真方法，对该车型后背门加载与约束的方式如图4所示，其中上面两个小三角形约束其所在位置的全部自由度，且约束位置为车身侧铰链安装孔。下面的一个小三角形约束其所在位置的平动自由度，且该约束部位为后背门锁扣所在的位置。以锁销安装孔的中心点建立多点约束的RBE2单元，且RBE2从节点连接内板及锁加强件边缘的一层节点。黑色箭头为所施加200 N力的方向。

图4 后背门各工况的边界条件

通过OptiStruct求解器进行求解，其弯曲及扭转工况下的位移变形云图如图5～6所示。

图5 扭转刚度加载点的最大位移

图6 弯曲刚度加载点的最大位移

企业对于该车型后背门刚度的校核标准为在规定载荷下，扭转刚度加载点的最大位移不超过2.5 mm；弯曲刚度加载点的最大位移不超过2 mm。从图5～6中可以看出，扭转刚度下加载点的最大位移为1.592 mm;弯曲刚度下加载点的最大位移量为1.494 mm，均满足企业的要求。

3 后背门的灵敏度分析

3.1 灵敏度分析理论

线性无阻尼自由振动的方程为

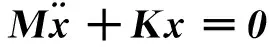
(1)

其特征方程则为

(K-ωiM)φi=0

(2)

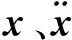
(3)

(4)

而OptiStruct软件中的灵敏度分析是利用优化方法中的梯度评估工具所进行的，即灵敏度S为

(5)

式中：x为结构设计参数所组成的向量；Δxi为结构设计参数的变化量；e为x同维数的向量，并且与Xi所对应的元素为1，其余都为0。

3.2 后背门灵敏度的计算

考虑到后背门组成的部件多，参考文献[11]先对其进行灵敏度分析以提高优化效率。将后背门的14个钣金件的厚度参数定义为设计变量，其中T1为后背门内板分件板，T2为右灯盒，T3为左灯盒，T4为盖锁加强板，T5为内外板的折弯，T6为内外板最外边一层的折弯，T7为后背门外板上段，T8为后背门外板下段，T9为后背门内板右分件板，T10为后背门铰链左加强板，T11为后背门铰链右加强板，T12为后背门铰链总成(左)，T13为后背门铰链总成(右)，T14为后背门内板。在OptiStruct中分别计算后背门质量、一阶固有频率以及扭转刚度灵敏度，其结果如表2所示。

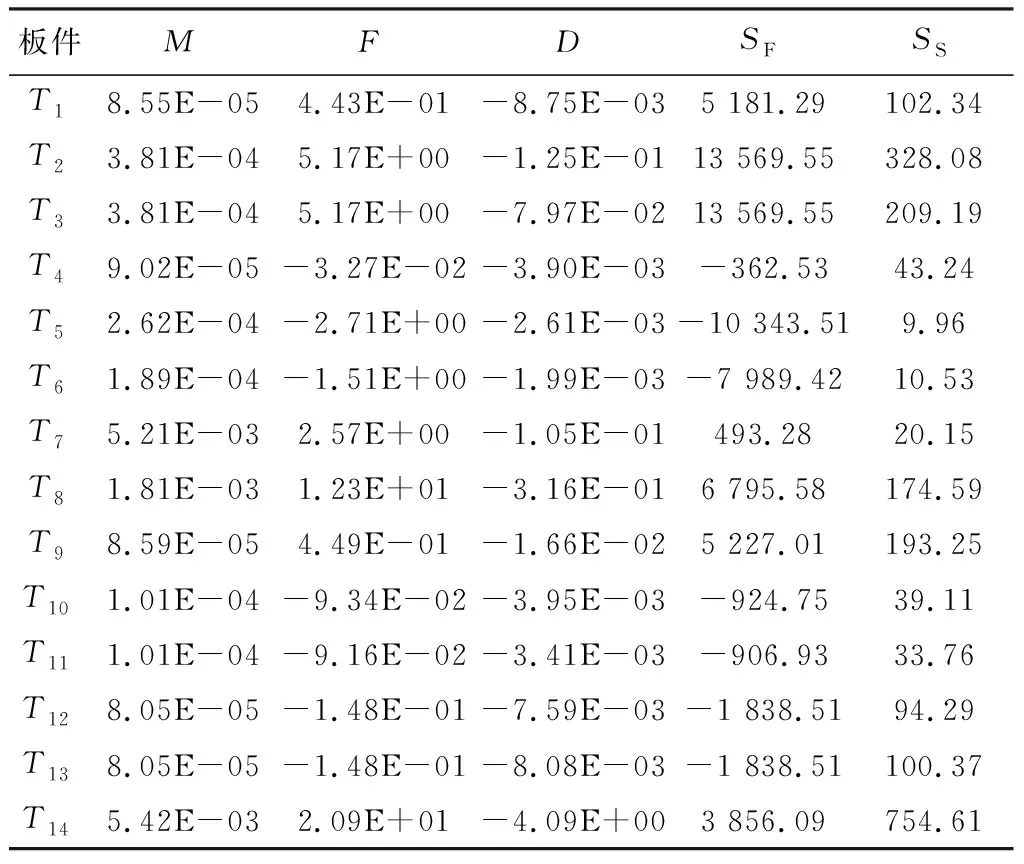
表2 后背门各钣金件灵敏度计算结果

基于优化目标与约束，考虑到后背门一阶固有频率和扭转刚度对质量的影响，定义一阶频率相对灵敏度和扭转刚度相对灵敏度[11]，分别为

(6)

式中：F为模态频率对于钣金件厚度的灵敏程度；M为质量对于钣金件厚度的灵敏程度；D为加载点位移对于钣金件厚度的灵敏程度；SF、SS分别反映的是一阶模态频率和扭转刚度对质量的灵敏程度。当SF与SS为正数时，表明厚度增加时其一阶模态频率和扭转刚度也会增加；当SF与SS为负数时，表示减小钣金件厚度也会使一阶模态频率和扭转刚度增加。

从表2可以看出应选择T2、T3、T5、T8、T9、T14作为多目标优化的对象。

4 后背门的近似模型

对于复杂的工程问题其计算成本是很大的[9]，需要消耗大量的计算资源且计算时间也长。作为一种代替手段，现代工程多采用近似模型进行分析。近似模型就是在寻求求解效率和模型精度的过程中出现的。在多数情形下，要拟合的变量与响应的关系大都是事先不知道的，所以需要引入实验设计和数值分析，在自变量的区域内进行采样，并在样本空间内寻求合适的逼近式来拟合自变量与实际函数的关系[12]，从而得到后背门的近似模型。

4.1 哈默斯雷实验设计

为了建立后背门模态与刚度的近似模型，需要通过实验设计的方法来获取样本点。常用的实验设计有哈默斯雷、拉丁超立方等。哈默斯雷采样适用于响应面为高度非线性的情况，在均匀性方面，它要比拉丁超立方表现得更好；而拉丁超立方采样特性的试验次数与变量的个数无关，也适用于响应面为高度非线性的情况。

在HyperStudy中以T2、T3、T5、T8、T9、T14为优化变量。以一阶扭转频率f7、一阶弯曲频率f8、扭转刚度加载点的位移d、后背门质量m为响应，并用哈默斯雷实验设计的方法来进行采样。其中因素个数为6个，得到28组样本数据。

4.2 基于移动最小二乘法的近似模型

后背门的近似模型就是利用移动最小二乘法在域Ω内构造出待求函数u(x)的近似函数uh(x)，待求函数u(x)在点x的局部域内可以局部近似为

(7)

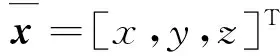
a(x)=[a1(x)a2(x) …am(x)]T

(8)

pi(x)为基函数，它可以采用单项式的形式，也可以采用其他线性无关的函数，应用比较灵活，但需满足以下条件：

p1(x)=1

pi(x)∈Ck(Ω)i=1，2，…，m

(9)

其中CK(Ω)为域内一系列k阶导数连续的函数。

使用哈默斯雷实验设计的方法得到样本数据，并采用移动最小二乘法近似模型来拟合后背门质量、一阶扭转模态频率、一阶弯曲模态频率以及扭转刚度。由于近似模型的精度对后续的优化分析非常重要，故采用方差分析中的R2来对近似模型的精度进行评价[7]。

(10)

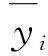
表3 响应面的精度

由表可知，用移动最小二乘法构造的近似模型精度符合要求，可将其作为代理模型进行后续的优化求解使用。

5 后背门多学科设计优化及结果分析

5.1 后背门多学科设计优化

多学科设计优化(multidisciplinary design optimization，MDO)与传统的优化方法不同之处在于，它可以将多种性能综合考虑，得到合适的优化结果，既避免了计算资源的浪费，节省了成本，也加快了计算速度。在设计汽车后背门时，需要考虑后背门的刚度、质量的大小和模态特性等多方面的因素。故对后背门的优化研究采用多学科的优化设计方法。

根据灵敏度分析所选定的6个钣金件的厚度作为优化的设计变量，以后背门的质量最小和一阶扭转模态频率为优化目标，以扭转刚度加载点的最大位移为约束。其数学模型为

(11)

式中：m为后背门的质量；f7为后背门一阶扭转频率；d为扭转载荷下加载点的最大位移；T1～T6为各个钣件的初始厚度；Timin为各个钣件厚度的下限值；Timax为各个钣金件厚度的上限值。采用自适应响应面法作为最后的优化算法，经过10次迭代后计算完成，其迭代过程如图7～10所示。

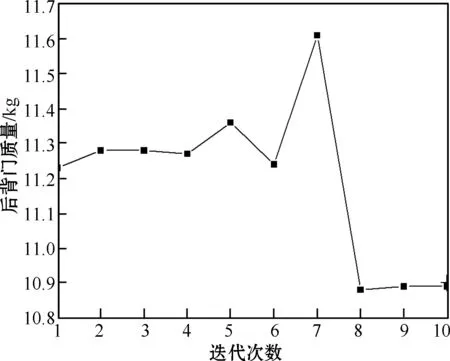
图7 后背门质量迭代过程

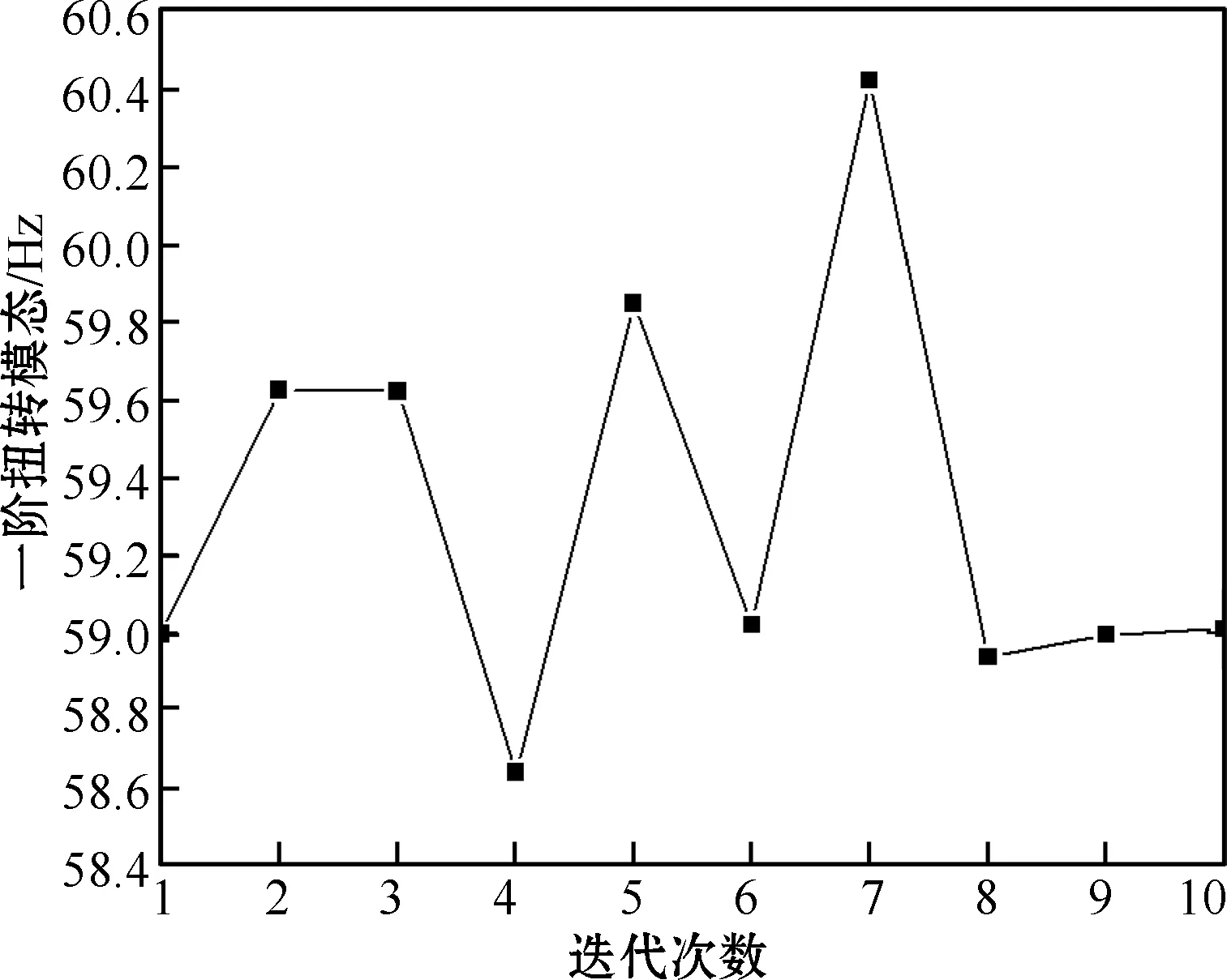
图8 扭转模态迭代过程

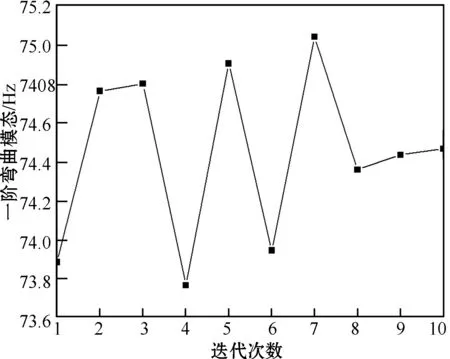
图9 弯曲模态迭代过程

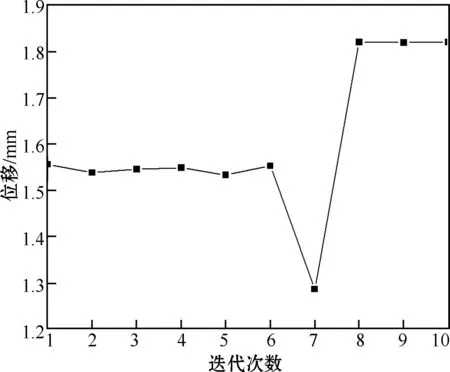
图10 扭转刚度加载点位移绝对值迭代过程

5.2 优化结果与分析

由于实际生产当中后背门钣金件厚度的精度为0.1 mm，故将模型优化后的值进行取整处理，其取整值如表4所示。把取整后的结果代入到有限元中进行再次计算，并与模型优化值进行对比，可得其一阶扭转和一阶弯曲模态频率误差分别为1.59%和1.10%，其扭转刚度加载点处的最大位移为2.02 mm。可以看出钣金件厚度取整后的仿真值与优化值存在一定的差异，但这更符合实际的生产。最终将取整后的结果与原始模型变量参数比较可得，在后背门扭转刚度加载点位移增加0.47 mm，一阶扭转、弯曲模态频率减小但满足企业要求的前提下，优化后的后背门质量比原后背门质量减少了0.5 kg。

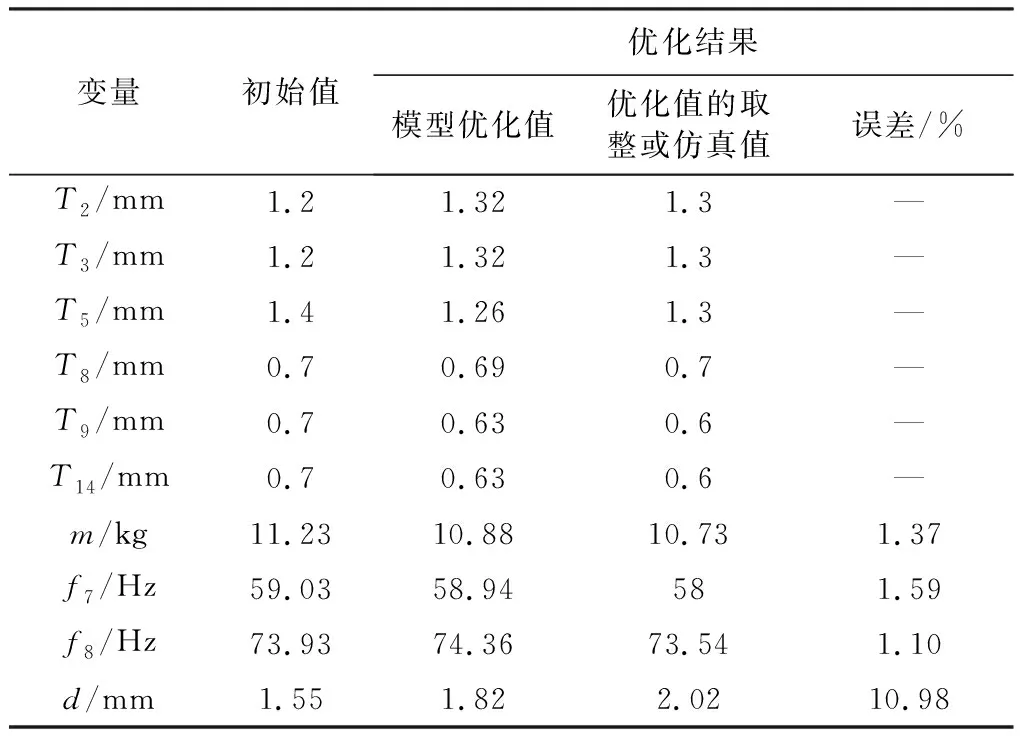
表4 后背门钣金件优化前后参数对比

6 结束语

为对某车型后背门进行轻量化优化，本文先用灵敏度分析找到影响后背门的质量、后背门的一阶模态频率以及扭转刚度的关键部件，并将其作为优化的设计变量。用哈默斯雷实验设计进行采样，并用移动最小二乘法构造出目标和约束响应的近似模型。在近似模型的基础上考虑后背门质量、模态频率及扭转刚度等几个主要指标，通过自适应响应面法进行优化。通过优化，在后背门模态频率和扭转刚度满足企业要求的前提下，后背门的质量减少了4.45%。