基于CATIA 的杠杆加载系统快速设计方法研究

刘海峰，刘 畅，覃湘桂

（航空工业成都飞机工业（集团）有限责任公司，成都 610091）

飞机在飞行时主要受到分布在飞机表面的空气动力载荷，在试验室内完全复现这种分布载荷尚不可能［1‑2］。因此，在飞机静力试验中，往往将这些分布式气动载荷折算成作用于加载点上的集中载荷。由于加载点数量很多，而试验中的作动筒数量则十分有限。因此在试验中，一般通过杠杆加载系统实现一个作动筒向多个加载点施加载荷。目前在杠杆加载系统的设计过程中，尤其是杠杆拓扑连接设计和载荷演算过程中，仍然依靠人为经验和手动计算，存在着工作量大、效率低等问题。

此外，杠杆加载系统主要由杠杆、连接件（拉环和拉板）、紧固件及胶布带等组成。此类零组件结构形式基本一致，尺寸大小有所不同。对杠杆加载系统的连接形式进行分析，可以分类并抽象出相应的装配约束形式。因此，运用参数化设计技术可实现这些零组件数模的“重用”和自动装配，极大提高杠杆加载系统的设计效率，缩短飞机静力试验的准备周期。

目前，国内的飞机结构试验还是主要通过二维工程图来表达杠杆加载系统的组成形式，尚没有专用的大型三维CAD 软件来支撑其设计。受限于开发技术与成本，目前杠杆加载系统软件的研发局限于一些小型的辅助计算程序，也无法与主流的CAD 软件进行数据传输。因此，在实际使用时，往往出现单位不统一、文件格式不一致等问题。如刘金玉等［3］编写了杠杆加载系统配重计算程序，可方便各级杠杆的配重计算，但该程序需要试验人员逐级输入杠杆信息，工作效率低。巴塔西等［4］开发了杠杆加载系统可视化软件，但该程序对数据输入要求苛刻，且只具有显示功能；杠杆加载系统设计过程中的大量零组件选型工作仍主要是依靠人工查表的方式完成，其实用性有限。陈江宁［5］研究了杠杆加载系统连接关系设计的方法，可以实现加载系统拓扑连接设计，但建立加载系统中形状各异的零组件建模仍需大量的人工交互。

本文基于CATIA 软件的CAA 二次开发平台研发了一套面向杠杆加载系统的参数化快速设计软件，涵盖了加载点自动计算、杠杆拓扑连接生成、加载系统参数化设计及自动装配建模等模块，并已成功运用于航空企业的型号试验任务，极大缩短了试验准备周期。

1 外形加载点自动计算

1.1 原始加载点信息

加载点是设计杠杆加载系统的基础，计算依据来源于飞机总体设计部门发放的外形曲面模型和数据文件，包括加载点编号、几何坐标和载荷信息，见图1。由图1 可见，除了座舱盖此类双曲度曲面给出了加载位置的三维坐标信息外，翼面类单曲度曲面（机翼、垂尾及边条翼等）则只给出了加载点在对称面上的二维投影坐标，而机身类曲面仅给出了加载点沿机身轴线方向的一维坐标信息（站位面位置）及该截面处总载荷大小。因此，软件需要结合不同的外形曲面及其加载几何信息自动计算加载点在飞机外形上的空间位置，为后续的杠杆拓扑连接设计和参数化建模提供依据。

图1 飞机外形数模和原始加载点信息Fig.1 Shape digital model of aircraft and original information of loading points

1.2 外形加载点计算

座舱盖类双曲度曲面的加载点位于初始外形数模上，只需计算该点在对应曲面上外法矢，并将其视为加载方向即可。翼面类单曲度曲面的加载点计算也比较简单，可计算投影方向的直线与外形曲面的交点。机身类曲面的加载点计算则比较复杂，原因在于：

（1）飞机外形曲面模型中存在大量的未裁剪的非流形曲面，难以进行求交计算；

（2）只给出了机身加载点的一维坐标信息和总载荷大小，导致无法计算加载点数量、位置和该点处载荷值。

针对上述原因，结合设计人员的经验和企业的实际情况，本文给出了一套机身外形加载点计算的标准流程，见图2。

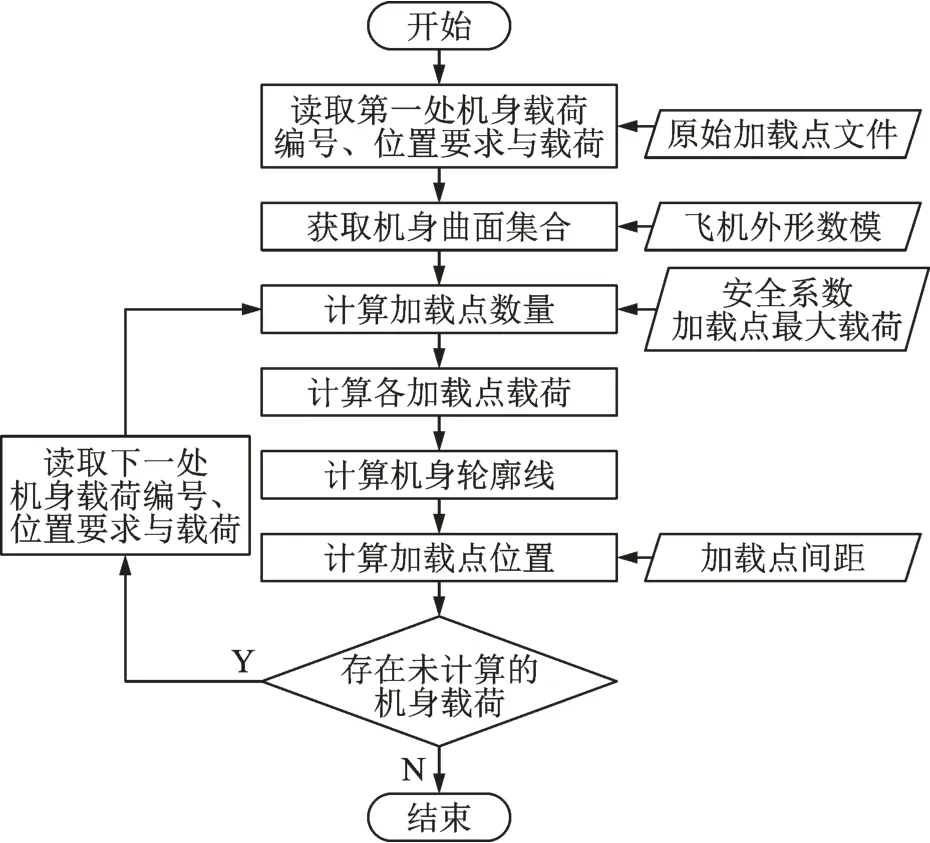
图2 机身外形加载点计算流程图Fig.2 Computation process of loading points on fuselage

主要步骤如下：

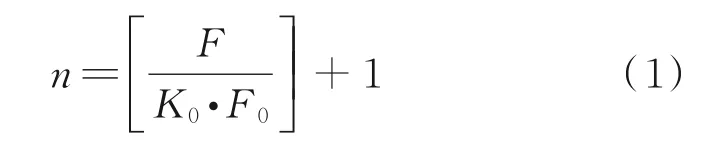
（1）计算加载点数量。根据经验计算公式（1）确定加载点数量。式中：n为加载点数量，F为机身载荷大小，K0为安全系数，F0为加载点最大载荷值。

（2）计算各加载点载荷大小。将机身载荷F平均分配至各加载点上，得到各加载点载荷大小均为F/n。

（3）计算机身轮廓线。根据试验人员要求，机身载荷的加载点沿机身轮廓线布置。若使用载荷所在的机身站位面与机身曲面进行求交，得到的结果不仅有机身轮廓线，还有机身站位面与飞机内部非流形曲面的交线，见图3（a）。针对此情况，本文采用直线簇与机身曲面求交的方式以获取离散的交点，其中直线簇的间距为1 mm。将得到的最外侧交点依次连接，即可得到机身的近似轮廓线，见图3（b）。

图3 机身轮廓线计算示意图Fig.3 Computation of fuselage outline

（4）计算加载点位置。根据数据文件中载荷的定义与给定的加载点间距，从机身轮廓线对应位置沿指定的方向在机身轮廓线上截取加载点。

1.3 外形加载点信息编码

加载点信息包括加载点编号、位置、载荷大小以及载荷方向。其中，加载点位置可直接存储于数模文件中，而载荷大小、方向等非几何信息则无法直接存储。本文将加载点信息进行编码，并以参数的形式挂接到CATIA 的特征树上来存储此类非几何信息。编码规则为：以加载点编号作为参数名称，将加载点三维坐标位置、载荷大小与载荷方向用逗号进行分隔。如图4 所示，参数的值从左至右依次表示加载点x轴坐标、y轴坐标、z轴坐标、载荷大小和载荷方向x、y及z分量。后续的计算中可从参数集中搜索参数值，并按编码规则进行解析即可获得加载点的所有几何与非几何数据。

图4 加载点信息存储Fig.4 Storage of loading-point information

2 杠杆加载系统拓扑连接设计

在计算出外形加载点的基础上生成杠杆拓扑连接关系是杠杆加载系统参数化快速设计的关键问题。所谓杠杆加载系统的拓扑即从已有的外形加载点集中按照一定的优化原则进行层次化的连接，直至最终生成唯一的连接根节点（即作动筒加载位置）。传统的设计方法是依靠人工经验，手动计算，导致设计效率低下。针对该问题，本文基于聚合层次聚类的拓扑连接关系生成算法，大大提高了拓扑连接关系的设计效率。在机器学习算法中，聚类［6］是一种无监督学习算法，简单说来即通过一定算法将相似的数据归为一组，达到分类的目的。每一分类可称之为簇，簇内的数据相似度高，而簇间的数据相似度低。层次聚类是聚类算法中的一种，通过计算不同数据样本间的相似度，确定数据样本的合并或者分裂顺序，进而创建一棵聚类树。层次聚类算法又分为自下而上的聚合层次聚类算法和自上向下的分裂层次聚类算法［7］。其中聚合层次聚类算法将每个数据样本看作独立的集合，然后依次将距离最近，即相似度最大的两个集合合并为一个新集合，直至终止条件被满足［8］，其过程与杠杆加载系统的拓扑连接生成十分相似。

传统的聚合层次聚类算法中相似度计算方法比较单一，无法满足杠杆加载系统拓扑关系设计过程中需同时兼顾加载点位置与加载点载荷的实际需求。本文对其进行了针对性的改进：通过改进相似度计算方法，优化了拓扑关系设计结果；通过优化聚类策略，有效地避免了连锁现象对拓扑关系设计的影响。

（1）考虑到集合中加载点的位置和载荷对集合间距离计算的贡献不同，对集合间距离的计算方式进行了改进。

在聚类算法中，使用距离矩阵表示集合两两之间的距离。初始距离矩阵可以使用一个n×n的矩阵来表示。其中，d(i，j)表示集合i与集合j之间的距离，为非负数。各集合与自身的距离取为0，且集合i与集合j间的距离具有对称性，即d(i，j)=d(j，i)。该距离矩阵可简化为一个上三角矩阵或下三角矩阵。一般情况下，两集合各指标间差异越大，则它们之间距离越大。

在聚类算法中，集合间距离的数学表达［9‑10］是十分重要的。不同的距离函数影响数据聚类的结果。常用的距离公式包括以下几种：

欧几里得距离

考虑到加载点信息包括了加载点位置和载荷大小两个变量，且量纲不同，在设计距离函数时需平衡两者之间的权重。陈江宁［5］选用了杠杆力臂比作为权重，参与空间距离加权计算。然而采用力臂比作为权重计算集合间距离时，容易出现距离相近的大载荷与大载荷组合，小载荷与小载荷组合的情况，导致连锁现象。

因此，本文采用两集合中加载点载荷之和与当前各集合中加载点载荷之和的最小值的比值为权重，计算加权的欧氏距离作为集合间距离

式中：d表示两集合间距，Ni与Nj表示集合中的加载点载荷之和，Nm表示当前各集合中加载点载荷之和的最小值，xi1和xi2表示集合i中加载点合力位置的坐标。

（2）为了减少连锁现象，提高聚类质量，对聚类集合的选取策略进行补充调整。

传统的聚合层次聚类算法将间距最小的两个集合进行合并，然而这种合并方式容易出现连锁现象［10‑11］。因此，本文对聚类集合选取的策略进行补充调整：在集合间距离大小与集合间距离最小值相近时，优先合并集合中加载点合力位置离加载区域合力位置更远的集合，如图5 所示。当3 组集合距离相近时，因集合4 离加载区域合力位置更远，优先将其与集合3 进行合并。

图5 改进的聚类策略示意图Fig.5 Demonstration of improved clustering algorithm

采用传统聚合层次聚类算法与改进的聚合层次聚类算法计算表1 中加载点对应的杠杆加载系统拓扑关系，得到的结果分别如图6、7 所示。

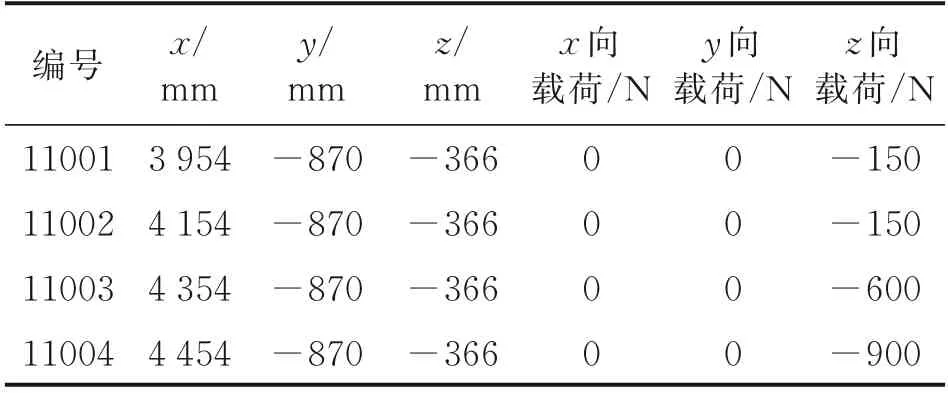
表1 加载点信息Table 1 Information of loading points

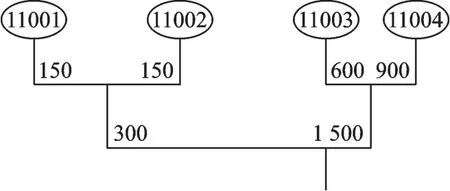
图6 传统聚合层次聚类算法计算结果拓扑图Fig.6 Computed topology using traditional hierarchical ag‑glomerative clustering algorithm

图7 改进聚合层次聚类算法计算结果拓扑图Fig.7 Computed topology using improved hierarchical ag‑glomerative clustering algorithm

传统的聚合层次聚类算法完全按照集合相似程度进行聚类，导致了连锁现象，最后一级杠杆力臂比很大。改进的聚合层次聚类算法则通过调整聚类集合选取策略成功解决了这一问题。此外，不难发现改进的聚合层次聚类算法通过降低杠杆力臂比，有效地降低了杠杆加载系统配重质量，从而降低了杠杆加载系统总质量，见表2。

表2 两种杠杆加载系统质量对比Table 2 Quality comparison of two lever loading systems

3 杠杆加载系统参数化设计

杠杆加载系统中使用的零组件依其功能分为杠杆、连接件、紧固件和配重件。如图8 所示，即是一个由3 个杠杆与7 个连接件组成的二级杠杆加载系统。

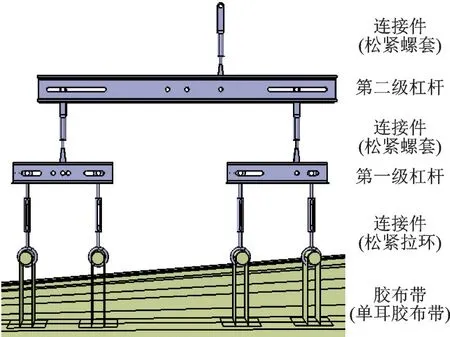
图8 杠杆加载系统Fig.8 Example of lever loading system

3.1 零组件参数化设计

CATIA 软件中，产品参数化设计［12］通常有两种方式：

（1）无CATIA 数模实例参数化设计。在该模式下，完全通过编程的方式，对零组件模型进行参数化驱动。用户输入参数，调用编制好的程序，产生所需形状的模型。此方法完全采用程序描述零组件建模过程，开发量大，且程序语句与设计者的建模思路密切相关。故该方法主要用于形状不规则的零组件快速建模，如贴合于飞机外表面的胶布带模型。

（2）有CATIA 数模实例参数化设计。此方法适用于可完全参数化的零件模型，利用CATIA 知识工程模块中的参数、公式和设计表配合编程的方式对已实例化的数模进行参数驱动。用户通过选择零组件型号，间接地输入参数，调用程序更新已实例化的数模。这种参数化建模方法特别适用于结构形式不变的零组件开发，如标准件库等。

3.2 杠杆加载系统的自动装配建模

在杠杆加载系统所有零组件参数化完成后，还需要对每个零件的装配约束进行定义，以便于开发程序实现杠杆加载系统零组件数模的自动装配［13］。以松紧拉环为例，对其安装关系进行分析：该连接件上部与杠杆连接，下部与胶布带中的铝棒连接。因此，可以通过3 处装配约束对连接件进行定位，具体装配约束的选择如图9 所示。将上部和下部圆环体中心点分别设为装配基准点，采用相合约束作为装配约束；将下部圆环体中轴线作为装配基准线，采用共线约束作为装配约束。

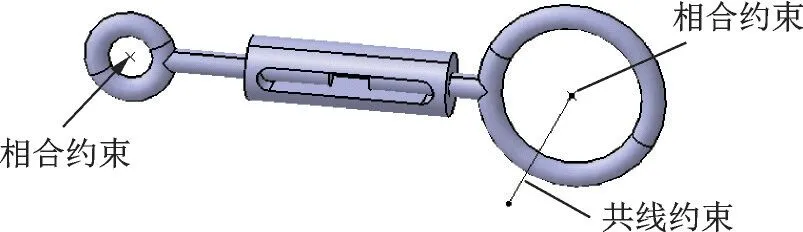
图9 松紧拉环装配的基准定义Fig.9 Assembly datum of elastic pull ring

4 基于CATIA 的杠杆加载系统开发

CATIA 是航空工业领域主流的CAD 软件，其参数化功能大量应用于产品的设计工作［14］。本文基于组件应用架构（Component application architec‑ture，CAA）二次开发平台，研发了杠杆加载系统快速设计软件，包括数据前处理、加载点计算及处理、杠杆参数化生成和自动装配建模等模块，模块划分如图10 所示。该软件的主要功能简述如下：

图10 软件功能模块划分Fig.10 Function module of software

（1）前处理模块。该模块引导用户完成加载点计算前的飞机外形曲面分类工作与禁布区设置工作，能够实现飞机外形曲面分类集合快速建立，曲面分类情况快速调整，禁布区快速设置与调整。

（2）加载点计算模块。该模块实现加载点快速计算，针对飞机不同部件上的加载点提供不同的加载点计算方法。

（3）加载点预处理模块。该模块实现载荷信息可视化，并引导试验人员完成加载点预处理。针对多项需要检查的加载点信息提供一键式的快速检查功能与异常加载点标记方法，实现异常加载点迅速筛选。

（4）杠杆加载系统快速设计模块。该模块实现杠杆加载系统拓扑关系快速设计与杠杆加载系统自动装配建模。实现了拓扑关系快速设计，并提供了拓扑关系调整，异常力臂比提示等功能。建立了厂标零组件库，实现了杠杆加载系统自动装配建模。

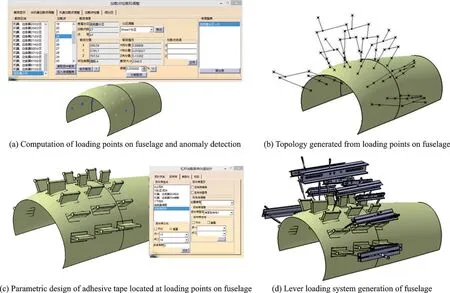
图11 机身某分区的杠杆加载系统快速设计Fig.11 Rapid design of lever loading system on some region of fuselage

5 结论

目前，我国的杠杆加载系统设计过程中仍存在人工参与程度高，设计效率低等问题。针对企业的实际需求，结合试验人员的经验，本文研究了外形加载点自动计算、杠杆连接拓扑设计算法、零组件的参数化设计和快速自动装配方法，研发了一套软件系统并成功应用于多个飞机型号的静力试验前的杠杆设计工作，极大地缩短了试验准备周期。本文的主要贡献包括：

（1）针对加载点计算自动化程度低、重复性高的问题，研究了不同区域加载点计算方法，实现了各区域加载点自动计算。

（2）提出了改进的聚合层次聚类算法，实现了杠杆加载系统拓扑关系快速设计；分析了杠杆加载系统零组件结构特点，规范了零组件设计过程，完成零组件参数化建模和杠杆加载系统快速自动装配建模。

（3）在CATIA V5R18 平台上，使用CAA 技术实现了集成度高，人机交互良好的飞机结构试验杠杆加载系统数字化设计软件，提高了试验室人员的工作效率。