基于装配约束的飞机导管几何特征建模与误差补偿

蓝玉龙，陈松林，高文翔，李帮义，唐沐天

（1.南京航空航天大学经济与管理学院，南京 211106；2.成都飞机工业（集团）有限责任公司，成都 610091）

金属导管作为飞机主要零件，大量应用在飞机液压、环控、燃油系统等关键部位，起到传递能源与动力的作用［1］。在飞机航行的过程中，机体内部各个子系统开始工作，导管结构需承受高压和高频振动［2］。当导管存在较大装配应力时，会导致管路发生漏气、漏油等现象，从而使飞机中各个系统发生失压、能源泄露、着火等故障，严重影响飞机系统的性能和安全［3⁃4］。因此，研究如何减小导管装配应力、提升导管安装质量，已成为国内外学者密切关注的话题［5⁃7］。随着基于模型定义（Model based definition，MBD）技术的普及应用，航空导管设计水平得到了很大提升，飞机制造厂可根据设计数模直接生产导管，但在实际生产过程中，按设计理论数模制造的导管在飞机上安装时往往存在误差，导致管路发生渗漏问题的情况时有发生。

导管安装过程的误差组成包括制造误差和装配误差。制造误差是导管制造产生的误差，在导管制造误差研究中，宋飞飞等［8］采用多元逐步线性回归方法建立了制造误差与导管工艺参数之间的预测模型，其预测精度控制在5%以内。导管装配误差由定位误差和结构装配误差组成。定位误差是指导管装配定位所引起的误差，如导管的安装角度误差和位置误差。结构装配误差是指安装导管的基准结构自身的误差［9］。在定位误差研究中，张宗郁［10］基于数字化装配角度对导管焊接装配进行了研究，采用专用夹具将焊接导管各段的坐标系统一到基准坐标系中，分析了法兰盘与导管轴线夹角的变化规律并提出了一种导管装配相对误差主动补偿方法。曾德标等［11］提出了自主数字化重构夹具柔性定位装夹方案，采用矩阵式定位器，通过控制导管各直线段端点位置达到导管定位的目的。以上研究对于导管制造领域中带有法兰盘的焊接类导管制造具有较好的定位效果，但在无法兰盘导管在飞机上装配应用中，无法直接使用理论坐标点对导管进行定位，导致现有方法无法有效地应用到无法兰盘导管装配过程中。

目前通用建模方法主要有基于笛卡尔坐标系的三维空间坐标变换补偿方法，以及在此基础上衍生出的基于增量的误差建模补偿方法等。针对导管类结构，利用向量来对其轴线进行建模和补偿能够提高计算效率，如向量公差模型（Vector toler⁃ance model，VTM）采用位置、方向、特征尺寸3 个变量描述零件空间位姿状态［12］，赖际舟等［13］提出的等效旋转矢量法，对惯导系统圆锥误差进行了补偿。基于此，本文提出了一种基于导管装配特征的误差补偿方法，用于在飞机结构装配误差始终存在的情况下，通过补偿导管设计理论模型参数，实现导管制造满足装配要求的目的。首先采用几何建模法与罗德里格旋转公式［14］计算并建立了导管装配过程矢量模型。在此基础上基于装配要求进行了装配约束分析，识别了导管装配关键特征［15］。随后分析了导管装配场景并分别提出了单约束和关联约束下导管装配误差补偿方法。最后以航空典型扩口导管为例进行误差补偿计算和导管装机气密性试验，验证所提出的误差补偿方法的有效性。

1 装配特征识别

导管安装误差体现在预装配环节，在两个扩口导管预装配时，导管的一端固定在飞机结构上，通过沿导管轴线旋转调整导管位姿，使其满足两个导管连接处的位置关系及与卡箍等周边结构的位置关系。图1 给出了两个扩口导管装配的结构示意图，导管1 可以用有序点集表示为

图1 导管装配结构示意图Fig.1 Sketch of pipe assembly structure

式中A1、A2、…、An和B1、B2、…、Bn分别表示端点A1、A2、…、An和B1、B2、…、Bn的坐标。

O1、O2分别表示导管1 和导管2 在飞机结构上的安装位置。两个导管的An端和Bn端实现连接。

为保证导管顺利安装到结构上，预装配过程需要满足结构装配要求，包括1 个基本条件和5 个装配特征。基本条件保证每个导管固定安装在飞机结构上，装配特征分为两个导管对接处的角度和距离约束、卡箍对导管中间部位的角度和距离约束、以及周边结构对导管的间隙约束。具体如下：

（1）基本条件

在将导管一端固定在飞机结构上时，采用螺纹连接，所以导管1 的A1点与结构端O1必须重合，且满足直线A1A2与结构O1端面保持垂直。导管2满足同样的要求。

（2）装配特征

①角度约束θ1：在两个导管位姿调整过程中，为保证连接处位置关系，导管1 和导管2 在连接端满足导管装配角度约束，即直线An-1An与直线Bn-1Bn的夹角θ1必须满足理论约束条件θ1≤[θ1]，其中[•]表示理论值。

②距离约束d1：在两个导管位姿调整过程中，为保证连接处位置关系，导管1 的An端与导管2 的Bn端满足距离约束，即d1=|An Bn| ≤[d1]。

③角度约束θ2：在两个导管位姿调整过程中，为保证导管与卡箍的位置关系，卡箍直线g1g2与导管直线Bn-1Bn的夹角θ2必须满足理论约束条件θ2≤[θ2]。

④距离约束d2：在两个导管位姿调整过程中，为保证导管与卡箍的位置关系，卡箍中心点G到导管直线Bn-1Bn的距离满足d2≤[d2]。

⑤距离约束d3：在两个导管位姿调整过程中，为保证导管与其他周边结构的位置关系，导管与周边结构距离d3满足|d3-h*| ≤[d3]。

其中角度约束θ1和距离约束d1是保证导管对接接头处密封性能的主要参数，该参数过大会导致导管基本的密封功能丧失，使飞机系统失效，此类问题发生概率较高，其重要程度最高，需优先满足。角度约束θ2和距离约束d2是反映导管固定卡箍与导管之间位置关系的参数，其大小主要影响导管装配后的应力，当应力过大时会使得导管发生渗漏、变形等问题，但此类问题发生概率较低，重要程度次之。距离约束d3是导管周边结构与导管之间的距离，其理论值被定义为h*。当距离过小时会导致飞行过程中导管与周边结构产生碰撞，导致导管损伤，但其发生概率较低，重要程度最低。

2 矢量建模

在特征识别的基础上进行基于装配特征的导管矢量建模。首先提取出导管轴线矢量理论值及其安装结构的轴线矢量实测值，然后建立实际装配状态下导管矢量模型。

2.1 轴线矢量提取

扩口类导管在与飞机结构固定端通常具有绕轴线旋转的冗余自由度，如图2 所示，导管1 可以绕轴线A1A2旋转。

采用旋转矢量法对导管整体空间位置进行变换时，需要导管矢量端点以及各个直线段轴线的矢量。对导管结构特征进行提取，包括导管接头点、直线部位、转折点，并用矢量集表示，如图2 所示，则导管1 和导管2 可以表示为

图2 导管装配矢量表示法Fig.2 Representation method of pipe assembly in vector⁃ization

导管1 安装结构O1的轴线矢量表示为s1，导管2 安装结构O2的轴线矢量表示为s2。

2.2 模型建立

在实际装配过程中，理想的导管装配模型与实际情况存在较大差距。如图3 所示，虚线部分表示导管2 的理论安装位置。因导管结构存在偏差导致导管安装后存在角度误差和间隙，为解决结构误差对导管装配精度的影响，需要结合装配误差对导管装配环境进行建模。

图3 导管装配模型示意图Fig.3 Sketch of pipe assembly model

图4 给出了结构误差环境下导管矢量模型，在导管1 固定的情况下，导管2 的理论安装位置如图中虚线部分所示，表示为矢量集b={b1，…，bn}，实际导管位置矢量集为b′={b'1，…，b'n}。在实际安装过程中，首先连接结构端点O2与导管2 的起始端点B'1，保证导管2 中矢量b'1与结构轴线s2平行，形成导管2 实际安装状态轴线b′。通过测量可以直接得到结构端点O2与结构轴线s2的实际位置。然后，结合导管2 的理论位置采用旋转矢量法对导管2 的实际安装位置进行计算。

图4 结构误差环境下导管矢量模型Fig.4 Vectorized model of pipe assembly in structural error

在计算过程中，采用罗德里格旋转公式，该方法采用空间轴矢和旋转角度两个要素对空间任意矢量进行变换。为确保导管2 的末端矢量b'1与结构轴线s2同轴，计算b'1的旋转轴与旋转角度。

（1）计算旋转轴eP

式中：norm( ⋅)表示计算矢量大小；eP1为旋转轴的单位矢量；α为旋转角。

3 误差补偿方法

3.1 装配场景分析

目前导管装配场景分为单约束装配和关联约束装配两种。图5 给出了两种装配约束场景。其中，图5（a）为单约束装配情况，导管的每段仅受来自单一结构的约束；图5（b）为关联约束装配情况，导管至少有一段受到来自不同结构的共同约束，如导管B3至B4段同时受到d1与d2的距离约束。

图5 装配约束场景分析Fig.5 Scene analysis on assembly constraints

3.2 补偿流程

图6 给出了导管装配误差补偿流程，主要有如下步骤：

图6 误差补偿流程Fig.6 Flow chart of error compensation technique

（1）计算出需要进行补偿的装配关键特征并对特征进行判断分类；

（2）分别补偿单约束特征和关联约束特征并确定补偿后的导管参数。

3.2.1 计算特征补偿量

补偿前首先识别出需要补偿的装配关键特征。上文中所列的5 项装配关键特征的边界条件表示为E1、E2、E3、E4、E5，如表1 所示。

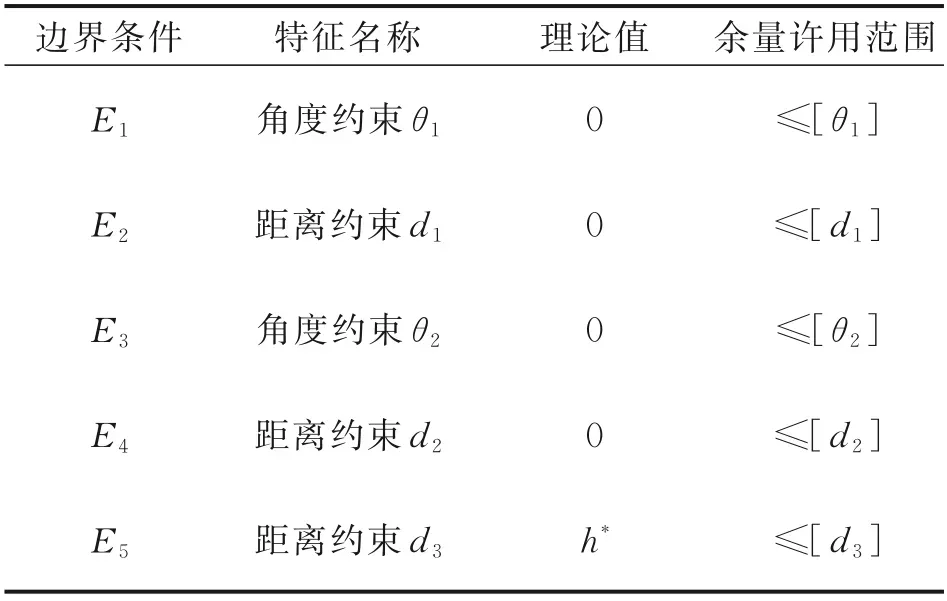
表1 边界条件余量对照表Table 1 Boundary condition allowance comparison table

调整后导管端点和矢量集可表示为b′={B1'，b1'，…，b'n}，其中B1'表示导管矢量起始端B'1的坐标，bi'(i∈[1，n] )表示各直线段矢量。计算导管调整后各边界条件满足程度，具体计算方法如下：

（1）计算边界条件E1，公差范围为[θ1]

（5）计算边界条件E5，公差范围为d3-[d3]

3.2.2 单约束特征补偿

针对导管装配矢量模型进行补偿，根据影响装配的重要程度对前4 项装配关键特征误差进行补偿，将导管分成单独的直线段进行补偿，然后对各直线段进行组合形成一完整的基于装配特征的补偿模型。当补偿过程中发现两个关键特征冲突时，按照特征的重要程度进行差异化补偿。

（1）消除导管1 和导管2 连接端的误差

该步骤涉及的装配关键特征包括角度约束θ1和距离约束d1。图7（a）给出了特征θ1与d1的误差补偿示意图，其补偿过程为通过平移、旋转的方式调整导管2 末端矢量b'n，使其与导管1 末端矢量an同轴，且首尾相连，即

（3）补偿后组合

通过（1）和（2）进行补偿后导管各段矢量已满足装配关键特征要求，通过保证矢量方向不变，调整矢量大小的方式使导管2 各直线段相交来补偿导管完整性，最终使导管2 成为完整导管。图7（c）

图7 导管装配关键特征误差补偿示意图Fig.7 Error compensation technique sketch of main char⁃acteristics of pipe assembly

3.2.3 关联约束特征补偿

当两个关键特征需在同一根矢量上进行补偿时，若完全补偿其中一项装配关键特征，可能导致其他关键特征超出许用值范围而无法进行补偿。图8 给出了导管对接处角度、距离误差和卡箍与导管2 直线段角度、距离误差冲突时的示意图，图中β1～β4分别表示卡箍轴线与补偿后导管2 第j根矢量的夹角、导管1 末端矢量an与补偿后导管2 第j根矢量的夹角、卡箍轴线与导管1 末端矢量an的夹角、导管1 末端矢量an与补偿前导管2 第j根矢量的夹角。d'1与d'2分别表示导管2 补偿后端点与导管1 端点的距离、导管2 补偿后直线段与卡箍中心点距离。具体计算方法如下：

图8 关键特征差异化误差补偿示意图Fig.8 Error compensation technique sketch of differenti⁃ated main characteristics

（1）β2～β4安装矢量夹角公式计算，其中β1为未知数

最后联立出角度约束β1与β2，距离约束d'1与d'2的不等式组

式中[θ1]、[θ2]和[d1]、[d2]分别表示角度约束θ1、θ2和距离约束d1、d2的许用值。

为优先满足两根导管对合处角度和距离误差β2与d'1，当求解出β1及点B′ 的空间坐标值(X，Y，Z)的取值范围时，优先保证β2与d'1取最小值，求解出β1及B′，代入式（17）后得到导管2 补偿后的理论矢量模型bth={Bth1，bth1，…，bthn}

4 试验与分析

对所提出的导管误差补偿方法和制造误差评估方法分别进行试验验证。图9 给出了生产现场某两根导管在理论状态下的安装结构示意，导管材料为铝合金材质，直径为20 mm，本文研究的是对导管预装配误差进行补偿，在导管预装配阶段，导管所受外力仅为导管自身重力，其引起导管自身形变可忽略。导管1 和导管2 在中间部位通过管接头连接，导管端部和中间部分受到飞机装配结构部分的约束。图10 给出了导管局部连接结构，其中导管扩口部分与管接头锥形面以及平管嘴锥面通过外套螺母的挤压形成密封，外套螺母与管接头通过螺纹连接产生轴向预紧力。

图9 试验导管安装结构Fig.9 Structure of experimental pipe assembly

图10 导管局部连接结构Fig.10 Connected structure of partial pipe assembly

表2 给出了导管1 与导管2 的理论模型参数，A1～A4与B1～B6分别为导管理论端点的坐标值，参考坐标系为飞机坐标系。表3 给出了两导管安装结构外形参数，包括结构1 和结构2 的端点坐标O1和O2、端点矢量s1和s2，以及其他约束相关的一些参数坐标。

4.1 补偿量计算

按照所提出的导管误差补偿方法对试验导管进行补偿。根据表2 提取得到的导管1 与导管2 的理论模型轴线矢量，以及表3 所测量得到的安装结构轴线矢量对导管2 进行基于装配特征的空间位姿调整。首先利用式（5，6）计算出导管2 的b1向量与安装结构轴线矢量的夹角α，然后利用式（7）计算导管2 旋转后的矢量集合b′。表4 给出了导管2调整后的参数值B'1～B'6。图11 给出了导管2 调整前后的空间位姿状态。

图11 装配环境下导管理论模型图Fig.11 Theoretical model of pipe assembly

表2 试验导管1 与导管2 理论模型参数Table 2 Parametric model of pipe 1 and pipe 2 (Theoret⁃ical)

表3 试验导管结构部分参数Table 3 Parameters of experimental pipe in structure part

通过计算可以得到导管2 调整前后末端点B6与B'6的距离为

然后，根据式（8～14），结合表3 给出的导管装配关键特征参数，对导管1 进行补偿。表4 给出了导管1 补偿后的参数，图12 给出了导管1 补偿后的空间位姿状态。

图12 导管补偿前后效果对比图Fig.12 Effect comparison before and after pipe compen⁃sation

表4 导管2 调整后及导管1 补偿后的模型参数Table 4 Parametric model of adjusted pipe 2 and com⁃pensated pipe 1

通过应用旋转矢量法对导管2 进行空间位姿调整，以及对导管1 进行基于装配特征的误差补偿，可以发现：

（1）所提出的方法能够有效地实现导管2 的位姿调节，通过实验发现调整前后导管2 端头距离偏差为1.589 3 mm，角度偏差小于1×10-4度。

（2）通过表2 和表3 的对比可以发现补偿前后导管1 的位姿发生了改变。

4.2 装配气密性试验

分别选取补偿前后的2 组导管进行装机、气密性试验，图13 给出了补偿前后的导管预装机效果。其中，图13（a）为补偿前的导管装机图，导管接头轴线和导管末端轴线存在明显偏斜；图13（b）为补偿后的导管装机图，导管接头与导管末端轴线同轴度较好。

图13 补偿前后导管1 实物装机对比Fig.13 Comparison of installed pipe 1 before and after compensation

根据航空工业标准HB4⁃1—2002《扩口管路连接件通用规范》，用恒定扭矩60 N·m 的扳手进行导管安装。然后根据装配气密性要求，对装配后的导管进行充气，使管路内部压力达到0.9 MPa，并保压时间5 min 观察管路压力变化。图14 给出了两根导管保压期间气压值变化情况，从图中可以看出所选用的两个导管在误差补偿前发生了泄压现象。然而采用误差补偿方法进行装配后的导管其内部压力保持恒定。

图14 导管1 补偿前后气密性对比图Fig.14 Airtightness comparison of pipe 1 before and af⁃ter compensation

装机试验结果表明所提出的误差补偿方法能够避免由安装环境引起的装配问题，提高了导管装配的气密性。

5 结论

本文建立了导管装配过程矢量模型，并分别提出了单约束和关联约束下导管装配误差补偿方法，通过导管装配误差补偿计算和导管装机气密性试验进行补偿方法验证。结果表明：

（1）所提出的方法能够有效地实现导管的位姿调节，通过计算得出导管2 端头距离补偿量为1.589 3 mm，角度补偿量小于1×10-4度。

（2）补偿后的导管在装机气密性上明显优于未补偿的导管。

本文在试验部分进行了单约束装配环境下的导管误差补偿方法验证，后续工作将进一步开展关联约束及其他复杂约束环境下的导管装配误差补偿方法研究及验证。