变批次长度的非线性分布参数系统迭代学习控制

李 勇，王玉川，陈晓雷，王游司

（重庆邮电大学工业物联网与网络化控制教育部重点实验室，重庆 400065）

迭代学习控制（Iterative learning control，ILC）是一种适用于在有限时间内重复完成给定任务的智能控制策略［1］。自Arimoto 于1984 年提出ILC以来［2］，受到广大学者的关注。经过30 余年的发展，ILC 被广泛应用于机械臂［3］、智能交通系统［4］、铸造［5］等重复过程［6］的控制应用中。ILC 作为一种简单且功能强大的控制策略［7］，经过不断发展，已经不再局限于微分方程描述的集总参数系统［8］，而是扩展到由偏微分方程所描述的分布参数系统［9］，并在分布参数系统得到广泛使用。如文献［10］建立了以双曲型、抛物型或椭圆型分布参数系统的迭代学习控制的设计与分析框架，能够处理参数或者非参数的不确定性。文献［11］针对一类系数矩阵不确定但有界的抛物型分布参数系统，提出闭环P型ILC 算法。与集总参数系统不同，分布参数系统的状态变量除了时间之外，还有空间变量，这使得其研究更具有挑战性。

现有的大部分ILC 文献研究的批次长度固定不变，使得ILC 在实际工程应用受到一定的条件限制，阻碍了ILC 的发展与应用。而在实际应用中，批次长度可能是随机变化的，这就意味着学习的过程可能提前结束或者推迟。例如人形机器人的步态问题［12］和生物医学中上肢运动功能电刺激等实际应用［13］。 最近几年，一些学者针对批次长度随机变化的ILC 问题做了大量研究［14⁃16］。其中文献［17］采用带有Arimoto⁃like 增益的P型ILC 算法，使得离散时间线性系统在批次长度随机变化的情况下，误差仍能够沿迭代轴渐进收敛。文献［18］则针对批次长度随机变化的离散线性系统中的ILC问题，提出了一种基于迭代平均算子的新型ILC 算法。Zhang 等将批次长度随机变化的ILC 首次运用于分布参数系统［19］。然而，现有文献中尚未有非线性分布参数系统的批次长度随机变化的ILC研究。

本文针对一类离散的非线性抛物型分布参数系统，根据该系统的性质和边值条件设计了P 型迭代学习控制器，给出了输出误差的收敛充分条件，证明所提控制方法在范数意义下跟踪误差的收敛性，并通过仿真验证了算法的有效性。

1 系统描述

本文主要研究类离散的非线性抛物型分布参数系统批次长度随机变化的迭代学习控制问题。考虑如下的非线性分布参数系统

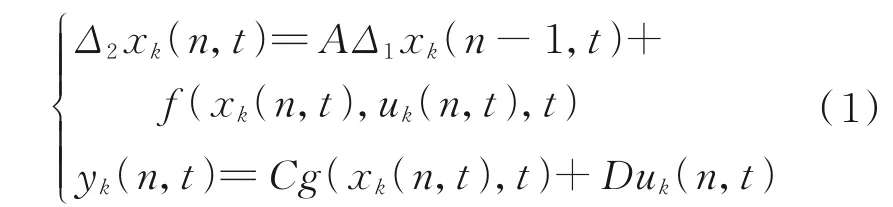
式中：n和t分别为空间和时间的离散变量，1≤n≤N，0≤t≤T，N和T是给定的整数；k=0、1、2…表示迭代次数；A、C和D为已知系统参数；xk、uk、yk∈R 分别表示系统（1）的系统状态、系统输入和系统输出。f：R×R×[0，T]→R，g：R×[0，T]→R均为非线性函数，且满足一致全局Lipschitz 条件

假设1 对于系统（1），任意的期望输出轨迹yd(n，t)，存在唯一的系统输入ud(n，t)∈R 使得

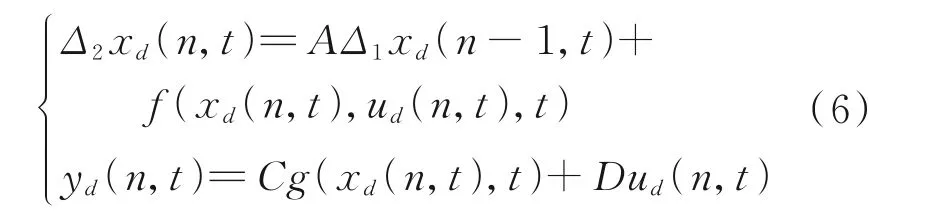
假设2 满足相同的初始条件，即xk(n，0)=xd(n，0)。在实际应用中，初始状态的每次迭代可能不会被精确地重置，但偏差在小范围内变化。

本文主要研究迭代学习控制中批次长度随机变化的问题，因此必须考虑期望批次长度Td与实际批次长度Tk之间的关系。当Tk＜Td时，输出信号yk(n，t)不包含t∈[Tk+1，Td]上的信息，这意味着系统输出信号不完整。当Tk≥Td时，系统可以输出整个批次长度信号，但是Td之后的信号对于学习而言是冗余和无用的，所以在本文中视Tk≥Td为Tk=Td。

2 算法设计与收敛性分析

2.1 算法设计

设计系统（1）的ILC 方案的难点在于系统的实际批次长度可能与期望的批次长度不同，即批次长度随机变化。在批次长度随机变化的情况下，为了描述系统误差在每一时刻发生的概率，本文考虑用随机批次长度发生的概率来定义系统误差。

定义1 随机变量Tk的概率事件分布为

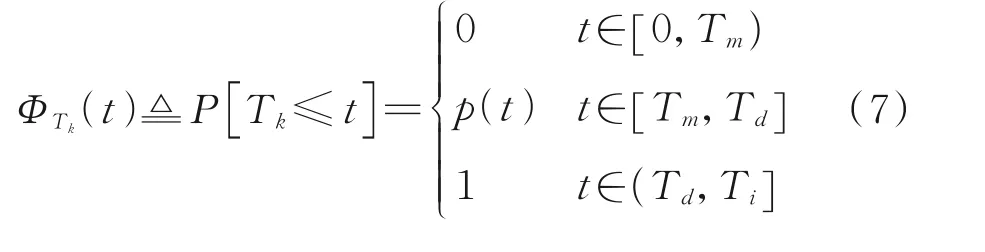
式中：Tm为系统（1）最小迭代长度，Ti为最大迭代长度。

此外，当t∈｛Tk+1，…，Td｝时，随机变量γk(t)服从伯努利分布，用于表示第k次迭代输出信息的有无。若γk(t)=1，表示系统输出在t时刻可测且输出在｛0，1，…，Tk｝之间有效。Ρ{γk(t)=1 }=q(t)表示系统误差信息在t时刻可测量的概率。若γk(t)=0，则表示无法获取t时刻系统输出误差的有用信息。此种情况发生概率为Ρ{γk(t)=0 }=1-q(t)。结合定义1 可得

2.2 收敛性分析

为了便于后续的收敛性分析，本文给出了以下的引理。

引理1［20］设{v(i)}，{B(i)}，{D(i)}为实数序列，且i≥0，由

3 仿真实验

图1 为系统期望输出曲面，图2～4 分别对应在迭代3、5、12 次后跟踪误差曲面。为了解变批次长度的ILC 算法对非线性抛物型分布参数系统的控制效果，本文将其与经典迭代学习控制算法［21］相比较。图2～4 的（a）图和图2～4 的（b）图分别是变批次长度的ILC 算法和经典ILC 在迭代3、5、12 次后的跟踪误差曲面。图5（a，b）分别是变批次长度的ILC 算法和经典ILC 在迭代第3 次和第12 次后的跟踪误差曲线。从图中可以看出，随着迭代次数的增加，两种算法的输出跟踪误差都逐渐减小，趋近于零。但是本文算法在迭代第5 次后跟踪误差几乎趋近于0，而此时经典算法的跟踪误差仍然相对较大。在迭代12 次后，本文算法的跟踪误差可以收敛到4×10-6，远远优于经典算法的5×10-3。

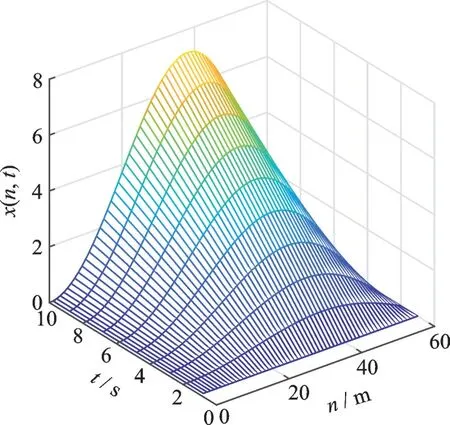
图1 期望输出yd(n,t)Fig.1 Desired output

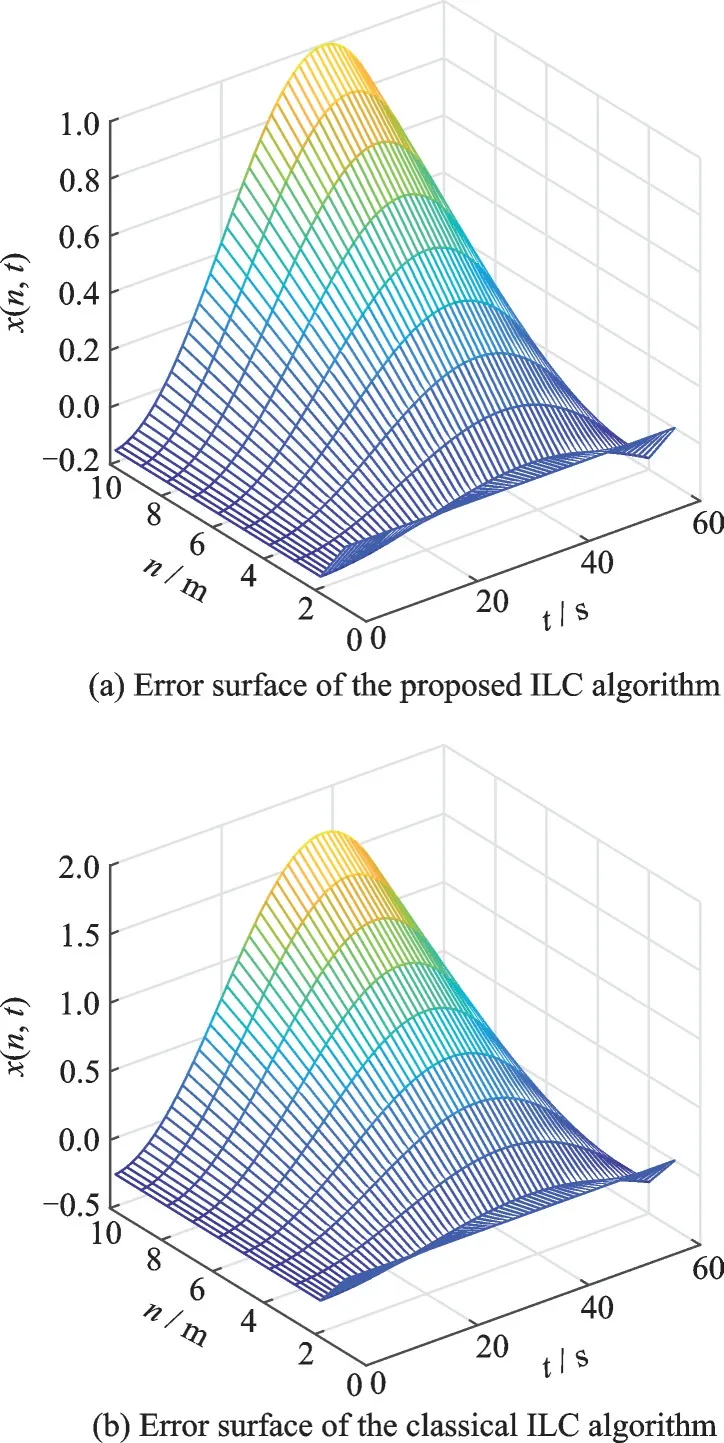
图2 误差曲面(k=3)Fig.2 Error surface (k=3)

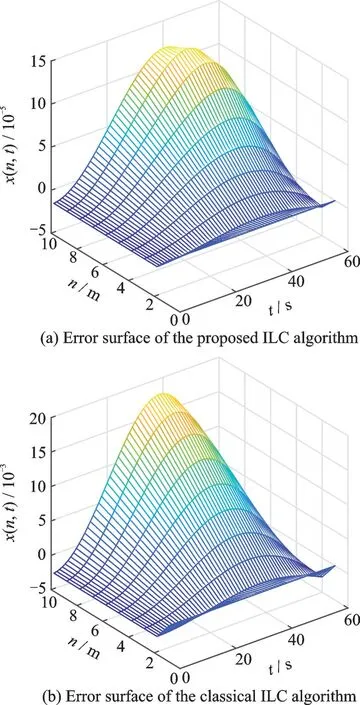
图3 误差曲面(k=10)Fig.3 Error surface (k=10)

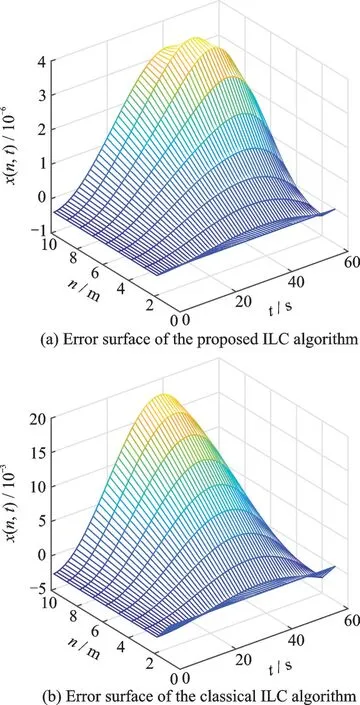
图4 误差曲面(k=12)Fig.4 Error surface (k=12)

图5 误差曲线Fig.5 Error curves

图6 是在迭代到第15 次时系统输出，与期望输出几乎一致，说明本文的变批次长度的ILC 算法可用于控制非线性抛物型分布参数系统。图7 是本文ILC 算法和经典ILC 算法的历次迭代最大误差曲线，通过图7 可知，所提控制算法收敛速度明显优于经典ILC 算法，验证了算法对系统（1）的有效性。因此通过对比，可以看出本文采用的算法明显优于经典迭代学习算法，不仅收敛速度更快，而且跟踪精度更高。

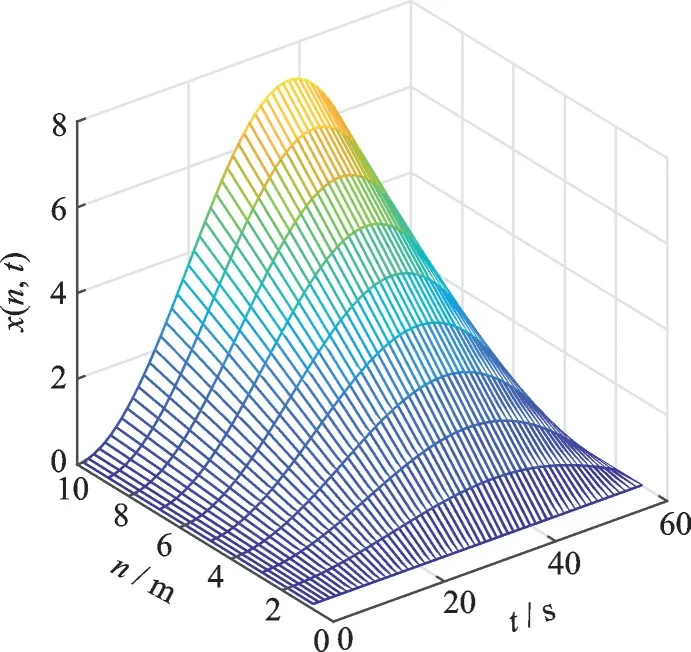
图6 迭代15 次系统输出Fig.6 The fifteenth iterative output

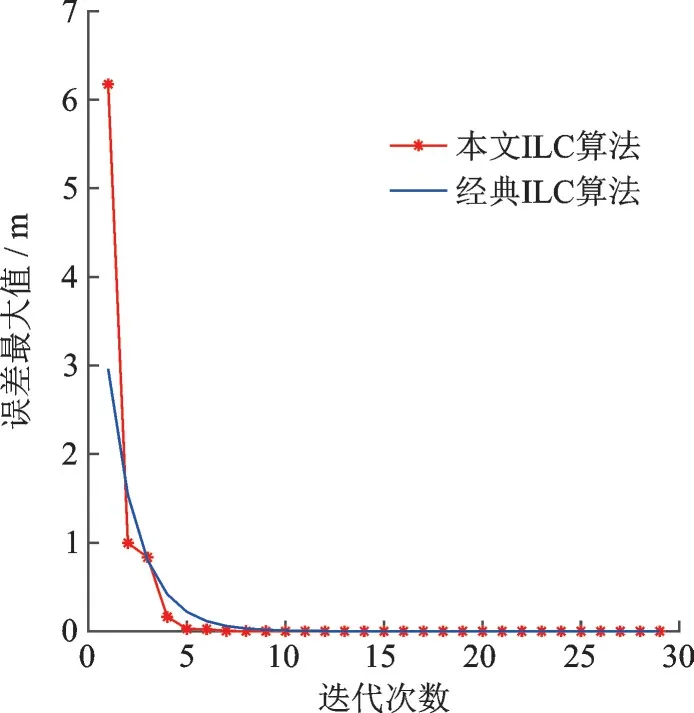
图7 迭代误差最大变化曲线Fig.7 Curves of iterative number-max tracking error

4 结论

本文将批次长度随机变化的ILC 算法应用于离散的非线性抛物型分布参数系统的控制，扩宽了ILC 算法在非线性分布参数系统上的应用，对分布参数系统迭代学习控制具有重要的理论和实际意义。此外，本文实现对期望输出的渐进跟踪，并通过严格的分析证明系统的跟踪误差在范数意义下的收敛。与传统迭代算法相比，变批次迭代算法收敛速度更快。未来将进一步考虑改进算法，以提高迭代学习控制在非线性分布参数系统中的可实施性。