内齿轮传动啮合齿面稳态温度场分析

张跃明，张 皓，纪姝婷，周天宇

（北京工业大学先进制造技术北京市重点实验室，北京 100124）

2K⁃V 行星传动装置采用两级减速传动组成，第一级减速为普通的外啮合齿轮传动，第二级减速采用内啮合少齿差行星齿轮传动。机构运动简图如图1 所示。2K⁃V 行星减速器作为一种高精密减速器对传动精度有很高的要求，此种情况下由热变形引起的传动误差不可忽略，因此对轮齿进行热分析有重要的意义。Mao［1］用解析法对齿轮进行热分析。Domnita Fratila 和Adrian Radu［2］用有限元方法对齿轮加工过程中的稳态温度进行仿真研究。薛建华等［3］精确计算了对流换热系数，并利用限元和热弹流结合的方法得到了齿轮本体温度场的分布。罗彪等［4］引进混合介质特性参数的比例因子以修正系数得到了齿轮稳态温度场和热变形。龚宪生等［5］分析了齿廓修形参数对温度场的影响。任敏强等［6］分析了不同工况下机车驱动系统用齿轮稳态温度场的分布。Handschuh 等［7］对螺旋锥齿轮进行热分析得到稳态温度场以及随时间和位置变化的温度场。

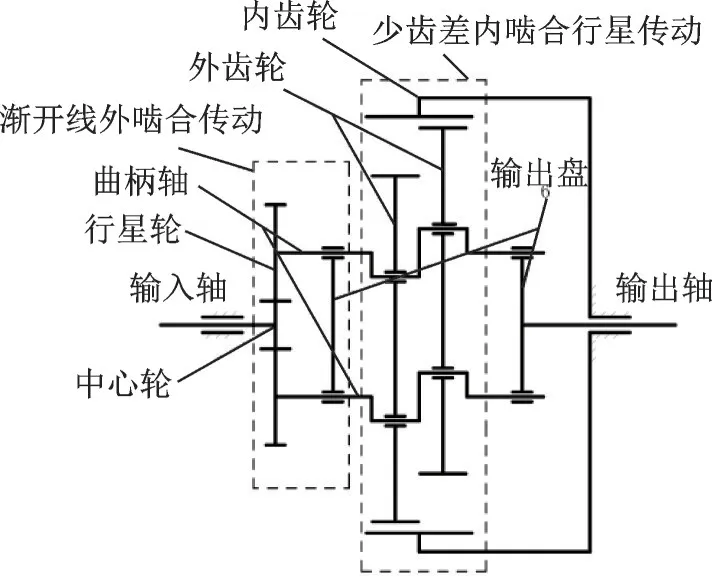
图1 机构运动简图Fig.1 Kinematic diagram of mechanism

本文取减速器中单个齿轮来进行分析。计算了不同啮合位置处摩擦热流量的数值以及各个表面的对流换热系数；并通过将啮合齿面划分成若干条形区域，来实现摩擦热流量的加载；采用有限元的方法，得到单齿的稳态温度场分布。

1 齿轮稳态温度场的理论基础

齿轮系统在传动过程中存在摩擦生热和齿轮接触面之间对流换热这两种状态。当生热和换热趋于平衡时，达到稳定状态，此时齿轮的温度基本不变。处于稳定状态之后的同一个齿轮上所有的齿，齿轮旋转一周的时间内所经历的过程是相同的［5］。所以取单个轮齿进行稳态温度场研究。单齿模型如图2 所示。

图2 单齿模型Fig.2 Single gear model

式中：hn为轮齿端面与周围润滑油表面传热系数；hd为轮齿齿顶面与周围润滑油表面传热系数；hg为齿根面与周围润滑油表面传热系数。

2 轮齿工作面摩擦热流量的计算

内齿轮和外齿轮在啮合过程中，为了保证齿轮正常传动，沿啮合线方向上的速度是相等的。而在与啮合线垂直方向上的速度是不相等的，产生相对滑动，齿轮间的摩擦热由此产生。内外齿轮在不同啮合点处的摩擦热流量由齿轮间的平均接触应力σk、相对滑动速度vk、摩擦因数f和热能转化系数γ共同决定的［3，8⁃9］。计算公式如下

2.1 摩擦因数

齿轮副在啮合过程中主要存在以下几个润滑状态：完全弹流润滑、混合润滑、边界润滑和干摩擦。

在实际传动过程中，齿轮的大部分区域处于完全弹流润滑状态。但是当条件达不到时，会出现不能形成的完整的润滑油膜，此时会发生由液体摩擦过度到干摩擦的情况，也就是边界润滑的情况的。综上所述，混合润滑是普遍存在的润滑状态。此时的摩擦因数可为［10］

2.2 啮合点相对滑动速度

由于2K⁃V 型行星减速器的内齿轮一般是固定的，在传动过程中外齿轮既有自转运动又围绕内齿轮中心进行公转，此种情况下直接计算相对速度比较困难。根据相对运动原理，将第一级和第二级减速机构转化为定轴传动，各个轮齿之间的相对运动关系并没有改变［11］。转换轮系中，内齿轮和外齿轮的角速度分别为

如图3 所示，B1B2为实际啮合线长度，内外齿轮在K点接触啮合。N1、N2分别为外齿轮和内齿轮的曲率中心。ra1、ra2分别为外齿轮和内齿轮的齿顶高半径；vK1、vK2分别为外齿轮和内齿轮啮合点处的速度。啮合点K到节点P的距离为

图3 齿轮啮合示意图Fig.3 Schematic diagram of gear meshing

由于每一个不同的rk值都对应着渐开线上的一个啮合点，所以由式（14）就可以得到任意啮合位置处内外齿轮的相对滑动速度。如图4 所示，当啮合点在外齿轮的齿根和齿顶附近时，相对滑动速度比较大，节点处的相对滑动速度为零。

图4 啮合点处的相对速度Fig.4 Relative velocity at different meshing positions

2.3 齿面间的平均接触应力

根据赫兹理论，内齿轮和外齿轮啮合时可以等效为两个圆柱体接触，圆柱体的半径为啮合点处的等效曲率半径［12］。齿轮的参数如表1 所示。

表1 齿轮基本参数Table 1 Basic parameter of gear

式中：T为外齿轮上的输入转矩；αK为接触点处的压力角；K为载荷分布系数，取0.5。

齿面平均接触压力为

2.4 啮合周期内平均热流量的计算

由式（7）所确定的摩擦热流量在内外齿轮上不是均匀分布的。此时需要引入摩擦热流量的分配系数β来确定内外齿轮上的热流量。

式中ω2为行星轮角速度。

当齿轮系统达到稳态热平衡状态时，把内、外齿轮在啮合面上实际接触时间内产生的热流量等效为一个啮合周期内的平均值。内、外齿轮上的平均热流量为

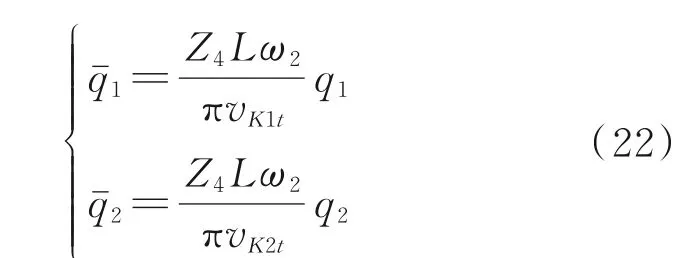
利用MATLAB 绘制外齿轮摩擦热流量分布曲线，如图5 所示。总体来看，在齿根附近的摩擦热流量比较大。

图5 外齿轮摩擦热流量的分布Fig.5 Distribution of frictional heat flux at external gear

3 轮齿表面对流边界的分析

当齿轮系统达到稳态温度时，润滑油的温度为70°时润滑油的性能参数如表2 所示。

表2 润滑油参数Table 2 Parameter of lubricant oil

根据表面在轮齿的部位不同，对流换热系数的计算分为以下3 种情况［5，13］。这里不再过多赘述。

3.1 端面对流换热

经计算此种工况下端面的雷诺数Re=2 673.1，润滑油在端面的流动属于层流，轮齿端面的对流换热系数hn可以表示为

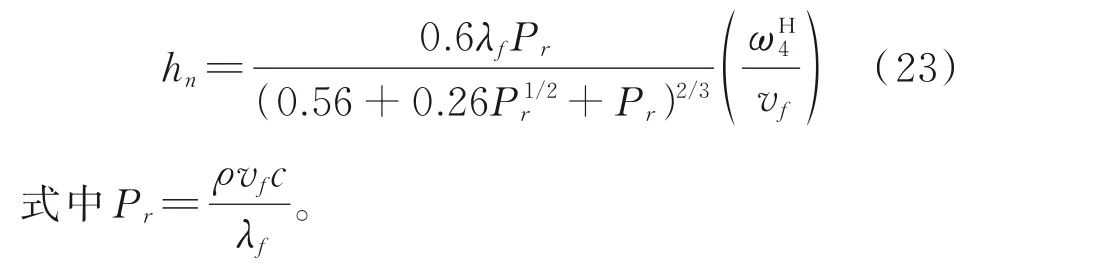
3.2 齿廓面对流换热

由于内外齿轮啮合的时间非常短，大部分时间齿廓的工作面和非工作面的散热情况是相同的，故认为两个面的对流换热系数相等。齿面的对流换热系数为

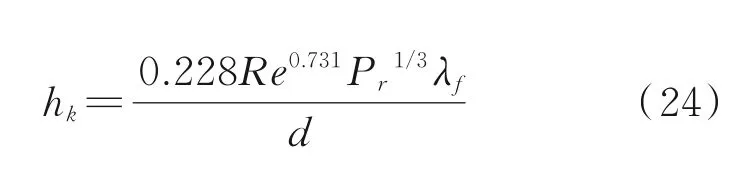
式中d为外齿轮节圆直径。

3.3 齿根面和齿顶端面对流换热

齿根面和齿顶端面均可以等效成细长平板，故它们的对流换热系数可以认为是相等的。

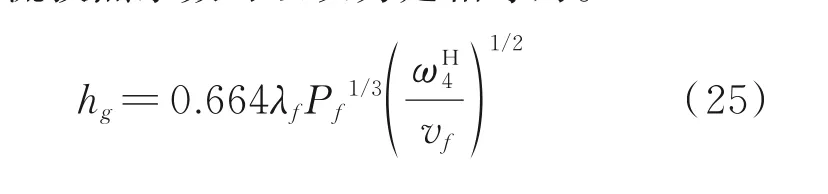
4 齿轮温度场有限元分析

利用Creo 软件绘制齿轮的三维模型，并切下单独一个轮齿导入Workbench，并将工作齿面沿齿宽方向划分成若干长条形区域，如图6 所示。

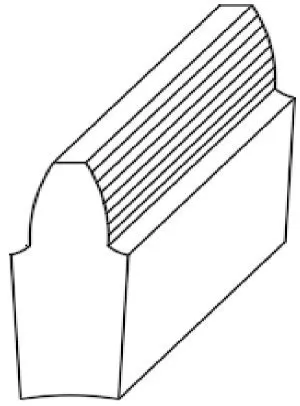
图6 条形区域的划分Fig.6 Division of the strip area

4.1 摩擦热流量的加载

经过上面分析可知，摩擦热流量的值随啮合点位置的不同沿着渐开线方向变化，而沿齿宽方向是不变的。所以，在加载热流量的时候可以取每个长条区域的两个端点处的摩擦热流量的平均值，将此平均值作为这个条形区域的热流量来加载［14］。

4.2 有限元结果分析

当条形区域的数量分别为15、30、40、60 时，轮齿的稳态温度场如图7 所示。由仿真结果可知，齿轮的稳态温度场沿齿宽方向是对称分布的，沿齿宽方向上中间位置温度高，两侧温度比较低。这是由于齿轮两侧的散热情况比较好且中间位置摩擦生热量比较大。

图7 齿轮稳态温度场Fig.7 Steady-state temperature field of gear

4.3 条形区域的数量对结果的影响

分别取条形区域的数量为10、15、30、40、50、60 时齿轮的最高温度和最低温度，如图8 所示。分析可知，随着条形区域数量的增多齿轮稳态温度场的分布大致不变，当划分的条形区域数量大于50份时，最低温度和最高温度变化幅度越来越小，基本趋于稳定。所以，以划分份数为60 的情况作为轮齿的稳态温度场。

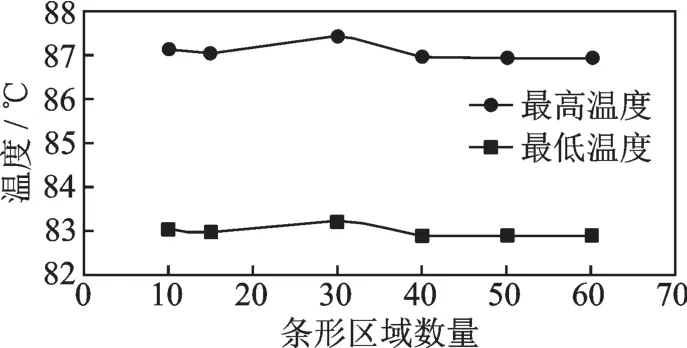
图8 不同划分份数的温度变化Fig.8 Temperature variation of different divisions

取条形区域数量为60 的轮齿进行分析，在啮合面上沿渐开线方向选取3 条路径线，如图9 所示，每条路径上点的温度分布如图10 所示。

图9 齿面上的3 条路径Fig.9 Three paths on tooth surface

图10 沿渐开线方向的温度分布Fig.10 Temperature distribution alone involute

由图10 可知，3 条曲线的走势一致。说明沿着渐开线方向，不同位置的温度变化趋势是一样的且最高温度出现在齿根靠近节圆的部分。

5 结论

（1）摩擦热流量的值和啮合点的位置有关，并不是恒定不变的值。当齿轮处于热平衡状态时，温度沿着齿宽方向是对称分布的，两侧温度低，中间温度高。

（2）划分的条形区域数量越多，结果越精确。当数量达到50 时，继续增加划分的数量，齿轮的温度场基本不变。

（3）在齿宽方向上的不同位置，温度沿着渐开线方向的变化趋势是一致的，最高温度出现在齿根附近。