等效弹性铰接体模拟单个桥节的海上浮桥计算方法
陈徐均, 黄 恒, 计 淞, 陈启飞
(陆军工程大学 野战工程学院,江苏 南京 210007)
作为一种应急交通工程设施,浮桥通常由多个桥节拼组而成。内河浮桥通常只需考虑水流和车辆荷载的作用,而架设在海上的浮桥则需要考虑波浪荷载的影响。由于海洋环境复杂多变,多个桥节连接而成的浮桥在复杂海洋环境中的动态响应是一个具有挑战性的科学问题。多位学者对此展开了研究,其中,Tajali等[1]对波浪荷载作用下不同连接方式的浮式栈桥进行了水动力分析。Raftoyiannis等[2]基于桥节为刚体的假设,研究了铰接浮桥在浮力、波浪力以及移动荷载作用下的动态响应问题。王志东等[3]基于Sesam软件计算并分析了柔性连接浮式栈桥在不同有义波高、不同谱峰周期波浪下的运动响应特性。苗玉基等[4]考虑地形的影响,对浮式栈桥在复杂地形下的运动响应进行了频域分析。为了研究多模块浮桥在规则波作用下的水动力响应和弯矩分布情况,孙建群等[5]进行了相应的水动力模型试验,并进一步分析了桥节接头非线性的影响。此外,Viuff等[6]基于短期极值方法对端部锚碇长浮桥进行了数值模拟,并且重点分析了浪向和周期等波浪参数对浮桥动力响应的影响。
实际作业时,增大浮桥单个桥节构型可以减少架设时的拼组作业量、提高车辆通行时浮桥的稳定性。但随着桥节构型的增大,其自身弹性变形将更加显著,这将导致基于刚体假设来计算铰接浮桥结构响应的方法会产生较大误差。在静水环境中,利用弹性基础梁模型可以分析求解浮桥的结构变形和受力[7],但是在波浪环境中,基于该模型求解浮桥的结构响应以及水动力问题则较为复杂。为了综合考虑波浪环境中浮桥的结构响应问题,本文提出了一种基于等效弹性铰接的多浮体模型模拟单个桥节的铰接浮桥动力响应计算方法。
1 理论模型
1.1 模型简介
图1为一个300 m长的浮桥布置示意图,该浮桥共由3个长度为100 m,宽度为16 m的桥节拼组而成,桥节之间通过光滑铰连接(释放桥节间相对纵摇运动、约束其他5个自由度相对运动)。浮桥垂直于海岸布设,波浪沿桥轴线方向入射。浮桥两端采用“八字形”布锚方式,内部采用平行布锚方式。在波浪荷载的作用下,不仅浮桥的各个桥节之间会产生相互运动,桥节自身也会发生弹性变形。为了解决波浪环境中浮桥的结构响应问题,提出了一种基于等效弹性铰接的多浮体模型模拟单个桥节的计算方法。

图1 浮桥布置图
如图2所示,该铰接浮桥的每个桥节均可以简化为一段弹性基础梁模型,并进一步离散为多个刚性浮体,桥节内部的刚性浮体之间通过弹性铰连接。在外部荷载作用下,浮桥将产生垂向变形。由于刚体本身不会发生变形,桥节结构变形通过弹性铰的转动来体现。因此,弹性铰的转动刚度对于结构的弹性变形至关重要。在同一荷载的作用下,弹性基础梁方法和铰接多浮体方法求解浮桥垂向位移会产生相似的结果,弹性铰的转动刚度便可通过这两种方法的位移等效模型进行求解。之后,将弹性铰的转动刚度以及离散后各个浮体的参数作为已知条件输入到水动力计算模型中,便可进行整个浮桥的水动力响应分析。

图2 弹性基础梁模型与铰接多浮体模型的转换关系
1.2 位移等效模型
1.2.1 弹性基础梁模型
单个浮桥桥节可以简化为一段两端自由的弹性基础梁。图3(a)为一段弹性基础梁模型,其在外部荷载作用下产生垂向变形。梁的左端为原点o,ox轴沿水平方向并与梁的长度方向重合,ou轴竖直向下。根据图3(b)中的本构关系,弹性基础梁上的任意位置x处的垂向位移u(x)、转角θ(x)、弯矩M(x)和剪力Q(x)具有式(1)中的微分关系和平衡条件[8]。

图3 弹性基础梁模型

(1)
式中:EI为弹性基础梁的抗弯刚度,E为弹性模量,I为梁横截面的转动惯量;p(x)为分布荷载,K为Winkler弹性基础梁模型的弹性刚度。对于水上浮体梁,其定义为
K=ρbg
(2)
式中:ρ为水的密度,b为梁的宽度,g为重力加速度。
当p(x)=0时,可以求得垂向位移u(x)的通解为

(3)

根据式(1)中的微分关系,对位移u(x)进行求导,可分别得到θ(x)、M(x)和Q(x)的表达式。
当一个外部荷载P作用在一段两端自由,长度为L的弹性基础梁的中间时(L/2处),梁的函数表达式将被分成两部分,对于荷载左侧的梁而言,其边界条件为

(4)
对于荷载右侧的梁,其边界条件为

(5)

(6)
相应地,θ(x)、M(x)和Q(x)也能通过代入相关系数得到。
1.2.2 多浮体模型
如图1所示,单个桥节被离散为由多个弹性铰连接的多浮体系统。假设一个两端自由的桥节被平均分为n个刚性浮体,所有浮体均为质量均匀分布的长方体。在进行多浮体模型分析之前,首先对单个浮体进行分析。如图4所示,每个浮体设置局部直角坐标系,坐标系原点F为水线面的中心,x轴和y轴分别沿浮体的纵向和横向,z轴垂直向上。点B和点G分别表示浮体的浮心和重心。l、b和h分别为浮体的长、宽和高,m为浮体的质量,t0=m/(ρbl)为浮体的初始吃水深度。

图4 单浮体几何示意图
根据浮体稳性计算原理,可以得到单个浮体的纵稳心高度为[9]

(7)
式中:Iy=bl3/12为浮体水线面平面相对于y轴的转动惯量;V=blt0为浮体的排水体积;实际情况中,浮体只产生小角度的倾斜,为简化计算,忽略浮体发生倾斜时几何非线性的影响,假设浮心B和重心G的位置相对于浮体保持不变,其垂向坐标可分别表示为zB=-t0/2和zG=h/2-t0。
基于纵稳心高度,可求得浮体绕y轴转动单位弧度(实际只产生小角度倾斜)所需要的力矩为
Ms=ρgVHx
(8)
外荷载作用下,多浮体系统中的所有浮体都将发生小角度倾斜。计算过程中,假定所有浮体的水平位移为零,且弹性铰的尺寸忽略不计。此外,相邻的两个浮体在铰接处具有相同的垂直坐标,对于第i个浮体,其底部两端的垂直坐标分别为wi-1和wi。第i个浮体的受力分析如图5所示,其主要受到自身重力、浮力、外部载荷以及相邻浮体的作用,当多浮体系统处于平衡状态时,可以得到力和力矩平衡方程分别为
mg+Pi-Qi-1+Qi-Ff=0
(9)

图5 多浮体系统受力模型


(11)
式中:k为弹性铰的转动刚度。

图6 相对转角与弯矩的线性关系
代入相关参数,式(9)和式(10)可分别化简为
位于两端的第1个浮体和第n个浮体,其边界条件均为一端自由,另一端与相邻浮体通过弹性铰连接,其约束方程的基本形式与第i浮体是一致的,只需要通过变换相应的边界条件就能得到它们的约束方程。
1.2.3 转动刚度的求解
式(12)和式(13)表示了所有浮体的边界条件,联立这些方程可得到多浮体系统的力学平衡方程组,并进一步用矩阵形式表示出来,可以得到
CU=P
(14)
式中:C为系数矩阵,U为未知数列阵,P为荷载列阵。其中未知数列阵和荷载列阵分别如式(15)和式(16)所示。
如1.1节中所描述的,当单个桥节中间位置(L/2处)施加荷载P时,其垂直位移可通过弹性基础梁模型和多浮体模型计算。桥节不同位置的垂直位移可以通过1.2.1节的弹性基础梁模型求得,对于多浮体模型,桥节各处垂直位移与弹性铰的转动刚度密切相关。假设基于两种模型的垂向位移变化近似相等,即多浮体模型中各节点的垂向位移wi-t0与弹性基础梁对应位置处的垂向位移u(il)的差值尽可能小,并将所有差值进行求和,建立位移等效模型,则可表示为

(17)
基于式(14)中的边界条件,利用最小二乘法对式(17)进行求解[10],便可得到弹性铰转动刚度k的值。
1.3 多浮体水动力模型
1.3.1 三维势流理论
图7为多浮体系统的坐标系,其中OXYZ为固定坐标系,oixiyizi和orxryrzr分别为第i浮体和第r浮体的局部坐标系。假定浮体所处的流域为理想流体,即流体无黏、无旋且不可压缩,波浪为微幅波,且只单向传播。多浮体周围流场的速度势可以表示为[11]


图7 多浮体系统的坐标系
流场中的速度势需要满足拉普拉斯方程和拉格朗日方程,此外,还需要满足物面边界、流体自由表面、海底边界面和无穷远处边界条件等。其中,入射势φI(X,Y,Z)作为已知条件,在有限水深中可以表示为
式中:Aw为入射波幅值,d为水深,α为波浪相位角,β为波浪入射角,η为波数,且满足色散关系ω2=gηtanh(ηd)。
绕射势和辐射势可以通过格林函数法求解。在得到流场速度势后,可进一步求解浮体所受的一阶波浪力和水动力系数。由于水动力计算部分主要基于ANSYS-AQWA软件完成,相关理论可参考文献[12],具体求解过程不在此处赘述。
1.3.2 运动方程
基于频域计算得到的浮体附加质量和辐射阻尼是随波浪频率发生变化的,因此可采用卷积形式建立浮体的时域计算方程[12]
式中:M为浮体的质量矩阵,A∞为浮体的附加质量矩阵,X(t)为浮体的运动位移列阵,C为浮体的静水恢复力矩阵,F(t)为浮体所受到的外部荷载,包括波浪力、水流力、系泊力等,h(t)为时延函数。h(t)可以表示为
式中:A(ω)和B(ω)分别为由频域计算求得的附加质量和辐射阻尼。
2 浮桥结构计算
基于等效弹性铰模拟浮体梁的相关理论方法的合理性已经在文献[13]中得到验证,本节主要对一个300 m长的铰接浮桥在波浪荷载作用下的动力响应进行研究。对于铰接浮桥来说,整个浮桥存在两种特性的铰,一种是基于位移等效原理得到的桥节单元多浮体模型之间的弹性铰,另一种为桥节之间的光滑铰,如果把光滑铰的转动刚度设置为0,则可以利用分析单个桥节的多浮体模型分析整座铰接浮桥。
2.1 模型参数设置
图1中展示了该浮桥的布置图。根据理论计算模型,将每个桥节平均划分为5个刚体,桥节内部的铰为弹性铰,其转动刚度可根据理论模型计算得到,桥节与桥节之间的连接通过光滑铰连接,浮桥计算主要参数如表1所示。图8为在ANSYS-AQWA中建立的浮桥模型,锚泊系统选用链径为32 mm的锚链,锚链的编号分别为M1~M18,其中端部锚的投锚距离为113 m,与桥轴线成45°夹角,中间锚的投锚方向与桥轴线垂直,相互平行的锚的投锚距离为80 m,波浪为0°规则波。图中P1~P5为浮桥上5个关键位置,它们分别为浮桥迎浪端(P1),第一个桥节的第二个弹性铰处(P2),桥节连接位置(P3和P4)和浮桥尾端(P5)。
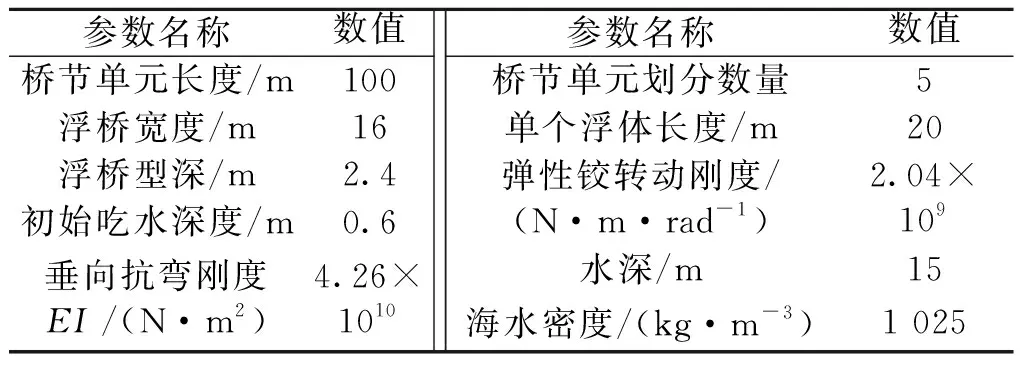
表1 浮桥主要参数

图8 浮桥ANSYS-AQWA模型
2.2 计算结果与分析
图9展示了波长分别为50、100、150和200 m的0°规则波作用下,浮桥不同位置处的垂向位移、弯矩和剪力分布的统计结果,其中,横坐标表示浮桥的不同位置,纵坐标为单位幅值响应结果(计算值除以波幅)。观察图中结果可以得到:波浪作用下,浮桥两端和桥节连接部位的垂向位移明显大于桥节中部,且迎浪端垂向位移最大,随着波长的增加,垂向运动也随之增加;桥节中部承受的弯矩最大;剪力的最大值通常出现在浮桥的连接部位。与垂向位移类似,随着波长的增加,浮桥承受的弯矩和剪力也都增大,但它们在某一波长波浪作用下出现峰值后又有所减小,这主要与结构和波浪的振动频率有关。

图9 浮桥不同位置结构响应幅值
为了研究波浪入射频率对浮桥结构响应的影响,统计了浮桥上5个关键位置(P1~P5)在不同频率波浪作用下的结构响应,结果如图10所示。图10(a)中结果显示,在低频波浪作用下,第一个桥节P2处的垂向运动响应幅值明显小于各个桥节的端部;高频波浪作用时,浮桥迎浪端(P1)的垂向运动响应明显大于其他位置,而此时P2处的运动响应与其他位置相差不大。图10(b)和图10(c)中结果显示,随着波浪频率的增大,P2处的垂向弯矩以及P2、P3、P4处的垂向剪力均为先增大,后减小,并在波浪频率为0.6 rad/s(波长为130 m)附近出现峰值,这也解释了图9(b)中波长150 m时弯矩响应幅值大于波长为200 m时相应值的原因。同时,该现象也提示我们,浮桥等浮式结构物需要依据架设海域波浪特性进行合理设计,以避免弯矩和剪力出现过大峰值。

图10 不同频率波浪下浮桥结构响应
锚链受力也是浮桥计算的重要部分,由于系泊系统对称布设,选取位于一侧的M1、M3、M9和M17四条锚链的受力进行分析。图11中展示了波高为1.0 m的不同波长规则波入射时,这4条锚链拉力的时域计算结果。在规则波的作用下,锚链力呈周期性变化,随着入射波长度的增加,锚链力的变化幅值也随之增大。当入射波长较小时,锚链拉力主要为预张力,波浪对锚链拉力影响较小,为减少作业量,此时可适当减少布设锚链的数目。


图11 锚链受力情况
由于M1和M17为“八字形”布锚方式,其受力不仅与波浪周期有关,还会受到浮桥纵荡的影响,故出现了锚链力随波浪和浮桥纵荡周期共同变化的情况。
3 结论
本文研究了基于等效弹性铰接多浮体模拟单个桥节的铰接浮桥动力响应计算方法,该方法可有效预测铰接浮桥在波浪环境中运动响应问题,文中计算了在不同波长的规则波作用下浮桥的垂向位移,弯矩和剪力分布特性以及系泊系统受力情况,可为浮桥的结构设计提供相应的理论参考。本文水动力计算借助了成熟的商用软件ANSYS-AQWA,在建模可视化,水动力系数计算以及结果后处理等方面均具有较为明显的优势。

