基于离散裂缝模型的页岩油储层压裂渗吸数值模拟

徐荣利，郭天魁✉，曲占庆，陈 铭，覃建华，牟善波，陈唤鹏，张跃龙

1) 中国石油大学(华东)石油工程学院，青岛 266580 2) 新疆油田公司勘探开发研究院，克拉玛依 834000 3) 新疆正通石油天然气股份有限公司，克拉玛依 834000

在当今页岩油等非常规油气商业开发的时代背景下，国内外普遍采用“大排量+大液量”的水平井分段压裂开发模式[1]. 与一般砂岩地层不同，页岩储层尽管注入大量压裂液，但压后返排率普遍较低，通常只有不到30%[2-3]，如加拿大Horn River盆地页岩储层的返排率在20%～30%之间[2]，北美的Haynesville页岩气田返排率低至5%[3]. 实践发现，较低的返排率并未给增产带来负面影响，相反关井时间越长，返排率越低，初期日产量却增加[4-7].研究压裂及关井阶段压裂液的渗吸作用机理及影响规律对关井及返排设计具有重要意义.

目前主流观点认为渗吸存在两种形成机理：毛管力和渗透压. Meng等[8]、Wang等[9]、张涛等[10]认为毛细管力是引起渗吸的主要作用机制，而Dehghanpour 等[11]认为页岩储层对压裂液的吸收不仅仅与毛细管力有关，渗透压也有显著影响.渗透压是半透膜两侧由于化学势差形成的压力差，包括两个要素：半透膜和化学势差. 页岩黏土扩散双电层在表面吸附和扩散运动的作用下形成“半透膜”，起到允许水分子透过、对盐离子限制的作用[12]；注入地层的低矿化度压裂液与地层高矿化度水存在浓度差，在页岩黏土形成“半透膜”后，即可在地层内出现化学渗透压. 渗透压的研究以实验和数值模拟为主. 杨柳[12]通过岩心实验研究了渗吸和离子扩散的相互关系. Zhou[13]等通过实验监测渗吸中页岩质量变化，发现渗吸过程中起初受毛管力控制，之后逐渐由渗透压主导.Fakcharoenphol[14-15]等将页岩基质分为有机质和无机质，通过数值模拟分析了岩石润湿性、重力、毛管力、渗透压等参数对返排率和产量的影响. 王飞和潘子晴[16]根据化学势差推导了渗透压公式，建立了考虑毛管力及渗透压的气水两相流动数学模型，分析了含水饱和度和盐浓度随返排时间的变化. 在渗吸的复杂裂缝的模拟方面，Almulhim等[17]和王家禄等[18]使用正交裂缝模型，将复杂的裂缝网络简化为正交的主次裂缝，通过局部对数加密技术精确模拟裂缝中的流动过程，但是复杂裂缝网络往往是不规则的，所以会造成模拟结果偏差较大. Fakcharoenphol等[14]以及王飞和潘子晴[16]采用双重（三重）孔隙介质模型，可以很好的研究多尺度渗流效应，但是未考虑复杂裂缝形态.

综上，目前国内外学者研究以毛细管力驱动的渗流机制研究为主[7,17-20]，虽然已有渗透压驱动的渗吸研究，但存在以下不足：（1）主要研究一维两相流[14-15]；（2）主要以返排率和生产效果为中心，因素分析中没有对关井渗吸引起压力、饱和度、浓度场进行深入研究[21]；（3）考虑渗透压的模型未考虑复杂裂缝形态[14-16,21].

基于此，本文采用离散裂缝模型，建立考虑毛管力和渗透压渗吸作用的二维油水两相流模型，通过对COMSOL Multiphysics进行二次开发，实现渗流场和化学场进行双向耦合，模拟压裂液注入和关井的过程，分析压裂水平井中的渗流和离子扩散过程，从而对压裂液在储层中运移和滞留机理和优化压裂返排制度提供理论和技术支撑.

1 数学模型

1.1 模型概述

本文采用离散裂缝模型，其可有效避免由于基质和裂缝之间毛管力相差悬殊，而导致在基质和裂缝界面计算困难的问题[22-23]. 建立了考虑渗透压的离散裂缝网络油水两相流动模型，包括渗透压方程、油水两相流动控制方程、盐离子运移控制方程以及边界条件. 对裂缝进行降维处理[24]，将裂缝简化为线性单元，研究区域（Ω）由基质（Ωm）和裂缝（Ωfi）组成，如图 1 所示.

图1 离散裂缝示意图Fig.1 Discrete fractures

1.2 渗透压

渗透压是由于半透膜两侧存在化学势差而形成的，理论计算公式为[25].

式中，V是水的摩尔体积，取 1.8×10-5m3·mol-1；R是气体常数，取 8.31×103Pa·L·mol-1·K-1；T是温度，K；aⅠ表示低盐度水的活度，aⅡ表示高盐度水的活度.

Fritz提出对于正负离子比例为1∶1的电解质（本文假设储层中只存在Na+和Cl-），渗透压的公式可以简化为[26]

式中：v是组成溶液的离子数量；C是溶液的盐浓度，mol·m-3.

1.3 盐离子运移控制方程

盐离子运移包括对流和扩散两部分. 盐离子扩散与浓度梯度相关，一般描述扩散的本构方程[15]：

由于流动引起的离子运移为[15]：

基质中盐离子守恒方程[16]

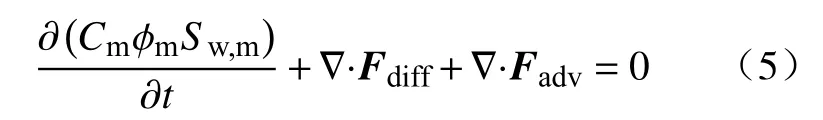
裂缝中盐离子守恒方程

式 中 ：Fdiff为 扩 散 作 用 产 生 的 通 量 ， mol·m-2·s-1；Eop为半透膜的效率，理想半透膜的效率为1，即不允许任何物质通过；D为扩散系数，m²·s-1； ∇为梯度算子，∇ ·为散度算子，Fadv为扩散通量，mol·m-2·s-1；u为流体流动的速度，m·s-1，Sw为含水饱和度；φ为孔隙度；下标m表示基质，f表示裂缝.

1.4 油水两相流动控制方程

储层中流体的质量守恒方程为[27]:

式中：m为流体质量，kg；t为时间，s；ρ为流体的密度，kg·m-3；Q为源汇项，kg·s-1.

式中：Sα为流体的饱和度；φ为孔隙度；下标α为流体种类，w表示水相，o表示油相. 孔隙度与密度都可写为压力的函数：

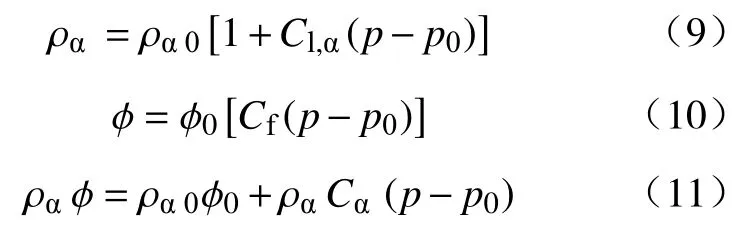
式中：Cl,α为储层流体压缩系数，Pa-1；Cf为岩石压缩 系 数 ，Pa-1；Cα为 综 合 压 缩 系 数 ，Cα=Cf+ φ0Cl,α；ρα0为 油藏 初 始压 力下 的 流体 密度 ，kg·m-3； φ0为压力为p0时的岩石孔隙度；p0为初始油藏压力，Pa.

渗流是在压力差和渗透压差两种压力作用下的渗流，考虑渗透压差作用下的流体渗流的运动方程:

式中：下标β表示基质或者裂缝（m或者f）；k为储层的渗透率，m2；krα为流体的相对渗透率；μα为流体的黏度，Pa·s；pα为油或水相的压力，Pa；Eop为半透膜效率.

再借助饱和度方程和毛细管力方程就可求解方程：

式中：pc为毛细管力，MPa.

渗透压是水相基质黏土孔隙流动的特有属性，因此，基质水相控制方程为：

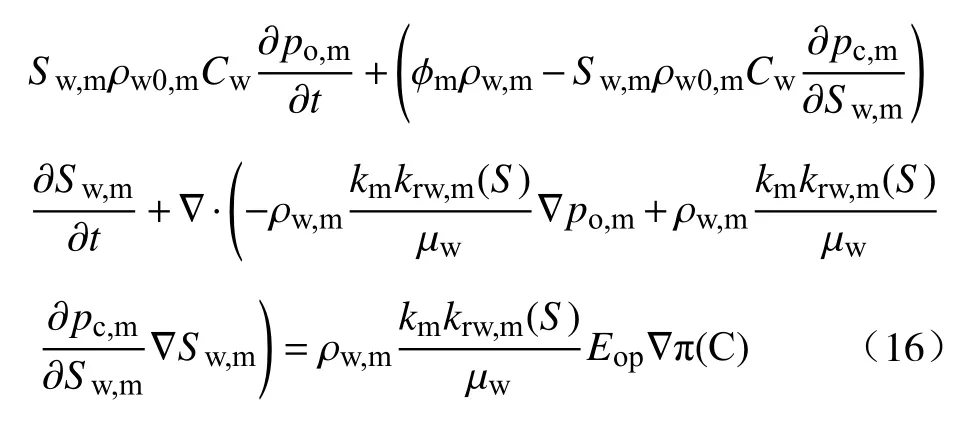
基质油相方程为：

裂缝水相方程为：

裂缝油相方程为：

页岩基质和水力裂缝采用不同的相渗曲线.基质相渗、毛细管力采用以下公式：

式中，krw,m表示基质水相相对渗透率；kro,m表示基质油相相对渗透率；pc,m表示基质毛细管压力，MPa；Se表示有效饱和度.

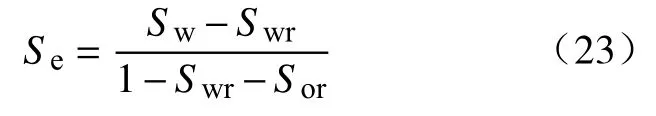
式中，Swr为束缚水饱和度，Sor为剩余油饱和度.

裂缝具有高导流能力，所以相对渗透率采用的“X”型相渗曲线，裂缝中的毛细管压力可以忽略不计.

为了更加真实的模拟压裂过程，需要在一定的压力下，短时间向地层注入大量滑溜水压裂液，注入过程中，近井筒周围的地层压力激增，裂缝宽度和基质孔径会增加，导致渗透率随着增大，所以可以下用如下的经验公式来表征[28]：

式中，km0为基质初始渗透率，m2；b基质应力敏感系数，取 0.101，MPa-1；Pnet净压力，MPa.

1.5 初始条件和边界条件

假设初始时刻为0时刻，注入时间t1，关井时间t2.

（1）初始条件.

模型未开始运行时，整个模型处于原始地层压力状态，初始条件为：

模型未开始运行时，整个模型处于原始地层含水饱和度状态，初始条件为

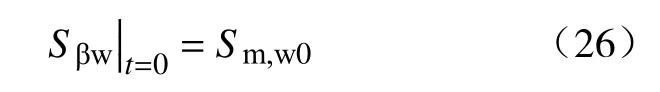
模型未开始运行时，页岩储层的盐度初始条件为：

（2）边界条件.

外边界为封闭条件，因此外边界条件为：

式中：n表示垂直于边界的向量，Γ表示边界.

恒定流量注入，渗流方程的内边界条件为:

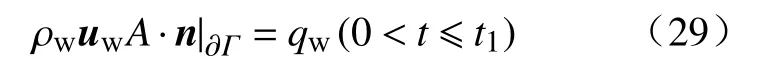
式中，A为横截面积，m2；qw为注入压裂液的流量，kg·m3·s-1.

压裂液盐离子浓度恒定，盐离子运移方程的边界条件为：

式中，Ci表示压裂液的盐离子浓度，mol·m-3.

2 模型有限元求解

使用COMSOL Multiphysic软件求解，该软件基于有限元法，针对多物理场提供了全耦合求解方法，能够在耦合分析中将耦合的各物理场联立起来形成一个统一的耦合方程组进行求解，同时计算得到各个独立场的因变量. 这种方法全面考虑了场与场之间的耦合效应，更接近于真实情况[21].

上文给出的各方程、边界条件以及初始值，构成了基于离散裂缝网络的油水两相流动-扩散控制方程. 通过式（5）～（6）、（16）～（19）对流体流动与浓度扩散进行双向耦合，流体运动会引起盐离子浓度的变化，由于页岩半透膜作用，盐离子对流扩散作用又会影响渗透压的大小，导致流体运动速度变化. 使用偏微分方程接口的对流-扩散方程对浓度场进行求解，两相流使用偏微分方程接口的系数型微分方程实现. 针对复杂裂隙网络的两相流模拟，一般采用厚度极小的薄层单元模拟[29]，但是这样会造成网格数量极大而难以运算. 本文对裂缝采用低维无厚度单元的形式[21]，将裂缝看作为整个域的内边界，在求解前通过在裂隙区域添加相应的控制方程的弱形式[30]来表征裂隙方程.

3 模型验证

3.1 渗透压验证

为表明本文建立的渗透压模型的正确性，使用COMSOL进行有限元数值求解，与Takeda等[25]的化学渗透压实验结果和Fakcharoenphol等[15]数值模拟结果进行对照. 图2和图3所示是储层1和储层2压力与盐浓度随时间变化曲线，其结果基本吻合，该模型反映了页岩储层盐浓度和压力的变化规律. 渗吸主要发生在注水初期，由于储层之间的盐度差较大和页岩的半透膜作用，只允许水进入储层1，所以造成了储层1的压力急剧升高，在0.5 d的时候达到顶峰. 因为页岩具有非理想半透膜的特性，浓度差还造成了离子扩散，由高浓度向低浓度扩散，随着时间推移，最终浓度达到平衡（如图3所示）.

图2 储层压力随时间变化图Fig.2 Reservoir pressure varies with time

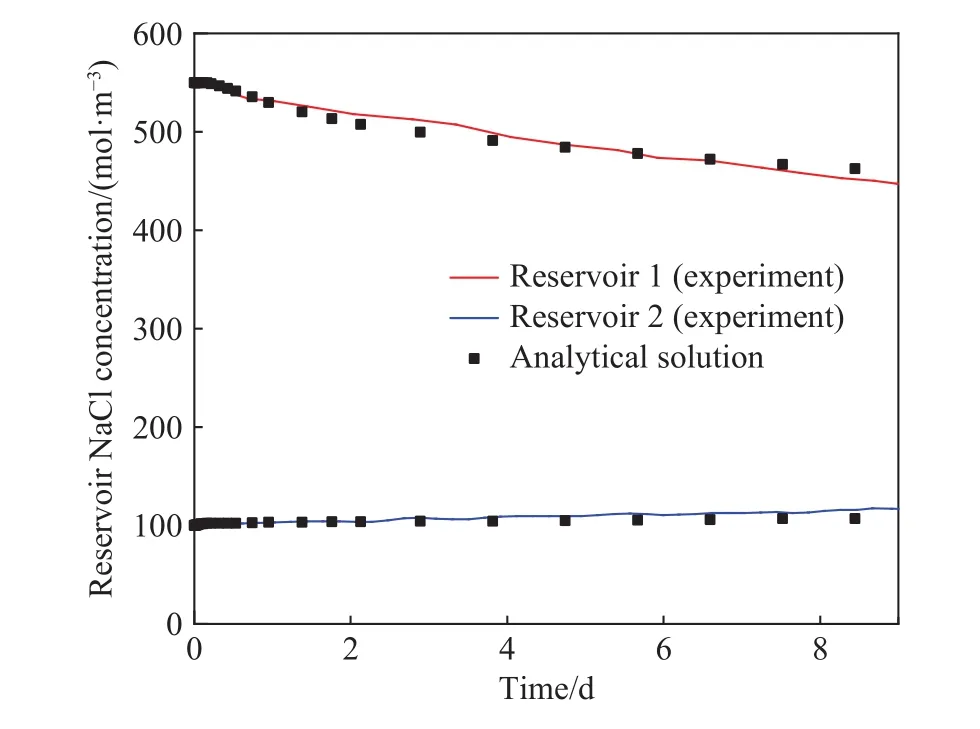
图3 NaCl浓度随时间变化图Fig.3 NaCl concentration varies with time

3.2 两相流验证

对复杂裂隙网络的模拟一直是两相流数值模拟的难点，为了验证本模型的有效性，将本模型使用的有限元方法与文献[31-32]提出的多尺度有限元方法及其实验结果进行对比分析，本次模拟左下角为注水井，右上角为生产井，模型中间一条“竖缝”，来模拟注水驱油的过程，见图 4（a），模型采用三角形网格进行剖分，见图4（b），使用文献[31]的基础参数，其模型中忽略了毛管力，基质和裂缝的相渗均采用X型相渗.

图4 物理模型（a）及网格剖分（b）Fig.4 Physical model (a) and mesh division (b)

图5（a）、（b）和（c）中分别为文献 [32]的实验结果，文献[31]的多尺度有限元法数值解和本文的有限元数值解，这些图中分别对0.1PV，0.3PV，0.5PV的含水饱和度剖面进行比较（PV为孔隙体积），可以发现本文的数值解与文献[31]实验结果有着高度相似的含水饱和度剖面，值得注意的是，在注入0.3PV时，裂缝下端稍微向左倾斜，在注入0.5PV时，油水前缘为圆弧状，这些特性都与本文的模拟是一致的，所以验证表明，该方法能够准确、有效的模拟含裂隙两相流动.

4 算例分析

页岩储层一般通过水力压裂技术短时间将大量滑溜水泵入井底产生大量连通裂缝，然后关井一段时间，再进行返排. 本文通过预置复杂裂缝和向地层泵入压裂液模拟压裂后的饱和度分布，然后进行一段时间的关井，观察其压力场，饱和度场，浓度场的变化.

4.1 模型参数

本文以新疆准噶尔盆地一口页岩油试验先导水平井为例，其采用密切割压裂方式实现体积改造. 文中裂缝采用随机建模，见图6，油藏、压裂参数参考文献[33-34]，盐离子运移参数参考文献[14-15].其中与水力裂缝连通的裂缝叫次级裂缝；随机分布且与水力裂缝、次级裂缝没有连通的裂缝叫未沟通天然裂缝. 考虑到运算速度，选取水平井其中1段（5簇）进行探究，簇间距15 m，见图7. 储层尺寸长度取3段段间距，探究压力波及范围，储层深2000 m，假设缝高50 m，注入1500 m3滑溜水压裂液，模型输入参数见表1.

图6 水平井多簇密切割分段压裂示意图Fig.6 Horizontal well-staged fracturing

图7 复杂裂缝几何模型图Fig.7 Complex fracture model

表1 模型参数Table 1 Simulation parameters

4.2 结果分析

4.2.1 毛细管力、渗透压与关井时间

为了探究页岩储层中毛细管力和渗透压在不同关井时间下对渗吸的影响作用，注入压裂液1500 m3. 通过设置4种情况来分析：（1）无毛管力，无渗透压；（2）无毛管力，有渗透压；（3）有毛管力，无渗透压；（4）有毛管力，有渗透压. 关井时间分别设置不关井，关井15 d，关井30 d，关井50 d.

图8为注入总液量的10%，50%，75%和100%时含水饱和度分布图，注入水首先沿着水力裂缝流动，之后分支流入次级裂缝，最后充满整个裂缝，图中在水力裂缝远端周围会出现低于初始含水饱和度的情况，这是因为注入水将油驱替出了裂缝，造成主缝远端附近含水饱和度下降. 随着注入水的增加，含水饱和度逐渐向两侧扩散，这表明了从注入开始已经发生了滤失作用，部分水进入基质.

图8 压裂施工注入过程中的饱和度分布图Fig.8 Saturation during injection in a fracturing operation

图9和图10分别为不关井和关井50 d后的饱和度，压力，盐浓度分布图，从图中可以看出关井50 d和不关井相比，发生渗吸的区域占据整个压裂段长，压裂段内的含水饱和度由1降至0.7左右，很好的解释了返排初期日产量与不关井相比较高. 图10压力分布图中中间裂缝的压力稍大于两边裂缝，这是由于裂缝压力向两侧扩散，中间簇裂缝压力发生叠加现象，造成了中间压力高于两端的现象. 并且压力波及范围显示，压力扩散会影响两侧压裂段.

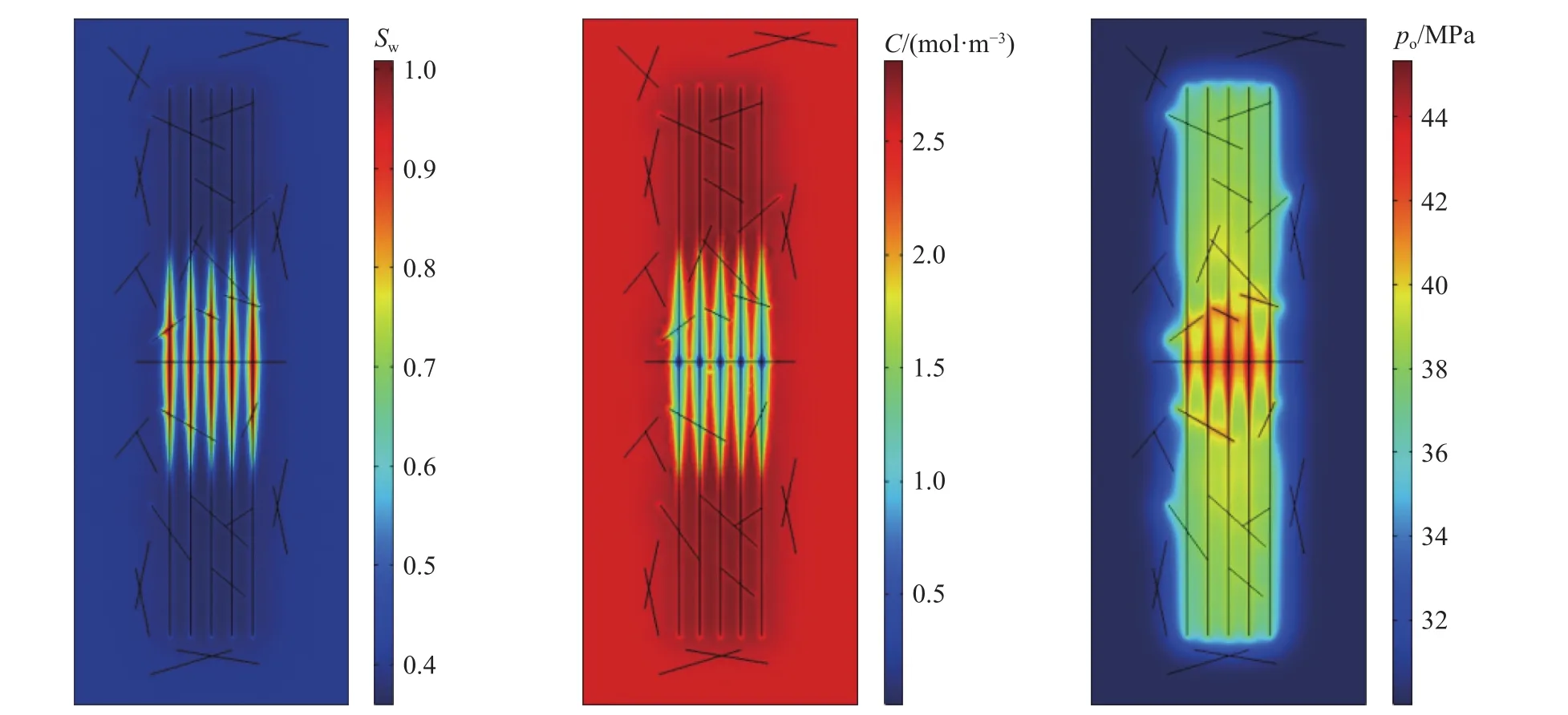
图9 不关井情况下的饱和度，压力，盐浓度分布Fig.9 Saturation, pressure, and salt concentration without shut-in

图10 关井50 d后的饱和度，压力，盐浓度分布Fig.10 Saturation, pressure, and salt concentration distribution after 50 days of shut-in

图11为不同关井时间沿裂缝中心x方向的含水饱和度剖面图，模拟结果表明压裂结束后，随着关井时间增加，裂缝处的含水饱和度迅速下降，裂缝两侧的饱和度逐渐升高，关井30 d后，渗吸量接近饱和，关井50 d后，根据最外侧簇含水饱和度分布，发现距离裂缝中心25 m的范围内发生了地层水重新分布，25 m之外的基质饱和度保持0.4，表明没有水侵入. 另外，15 d渗吸量可达总渗吸量的78%左右.

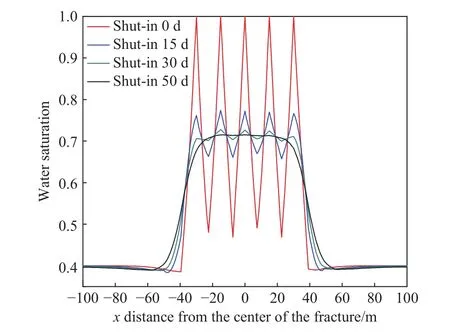
图11 不同关井时间下的饱和度Fig.11 Saturation at various shut-in times

图12为不同关井时间距压裂裂缝不同距离的盐浓度剖面图，两侧压裂段盐浓度的扩散范围大约30 m，比水的渗吸范围多5 m，这是由于盐离子的扩散作用造成的，虽然页岩储层存在半透膜，但是半透膜效率只有10%，所以只会阻隔小部分离子通过. 盐浓度关井15 d和关井50 d后分别为279.5 mol·m-3和 353.5 mol·m-3，表明前 15 d 盐浓度即可提高了80%.

图12 不同关井时间下的盐浓度图Fig.12 Salt concentration at various shut-in times

图13为不同时刻下距压裂裂缝不同距离的压力剖面图，在注入结束后，中间簇受到两侧压力叠加达到45 MPa，高出初始地层压力12 MPa.随着关井时间的增加，裂缝处压力不断降低，并逐渐向两侧扩散，扩散速度随与裂缝两侧的距离增大而减慢. 关井50 d后沿着水平方向距离裂缝100 m左右的位置压力降至31 MPa，与地层压力接近.

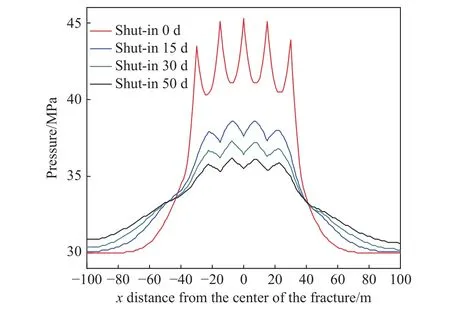
图13 不同关井时间下的压力图Fig.13 Pressure at various shut-in times

图14对比了有无毛细管力和渗透压在关井50 d后含水饱和度的变化，模拟结果显示，毛细管作用和化学渗透作用都有助于水进入储层基质，加剧水向地层的滤失. 关井50 d后，当驱动力仅仅为压差时，裂缝处的含水饱和度由1降至0.79，当驱动力分别为毛细管力和渗透压时裂缝处的含水饱和度由1降至0.76和0.74，这说明了在压裂液关井渗吸过程中由压力驱动的流动占主导地位，当驱动力同时包含毛细管力和渗透压时，裂缝处的含水饱和度由1降至0.71，表明当渗透压和毛细管力联合作用，会使更多的水滞留在地层中，这也是压裂返排率过低的原因.

图14 不同关井时间下的饱和度图Fig.14 Saturation at various shut-in times

4.2.2 盐浓度

对于含黏土矿物较高的页岩储层，发生反向渗透和蒸发等作用，随着时间的积累，储层水的矿化度可高达4.78×103mol·m-3. 由于注入低盐度压裂液与地层水产生巨大的浓度差，形成渗透压驱动水进入地层深处. 此外返排液中离子浓度明显升高，因此分析储层盐浓度对渗吸的影响作用和盐浓度在储层中的扩散规律很有意义.

图15是不同时期不同矿化度沿x轴的盐浓度剖面图，其中注入水的盐浓度为17.1 mol·m-3，地层水盐浓度分别取171、2.565×103和4.786×103mol·m-3，图中可以看出不同地层水盐浓度导致扩散速度不同，扩散距离也有所差距，盐离子的运动主要受到对流和扩散的共同作用，盐浓度差较大时，扩散速度较快，并且高盐度差会强化渗透压的渗吸效果，增加水的波及的范围，使得裂缝处含水饱和度较低（图 16）. 地层水矿化度 4.786×103mol·m-3时，关井50 d后，裂缝附近的矿化度接近600 mol·m-3.

图15 不同矿化度下的盐浓度分布. （a）泵注后；（b）关井后Fig.15 Distribution of salt concentration under various salinity levels: (a) after pump injection; (b) after the shut-in

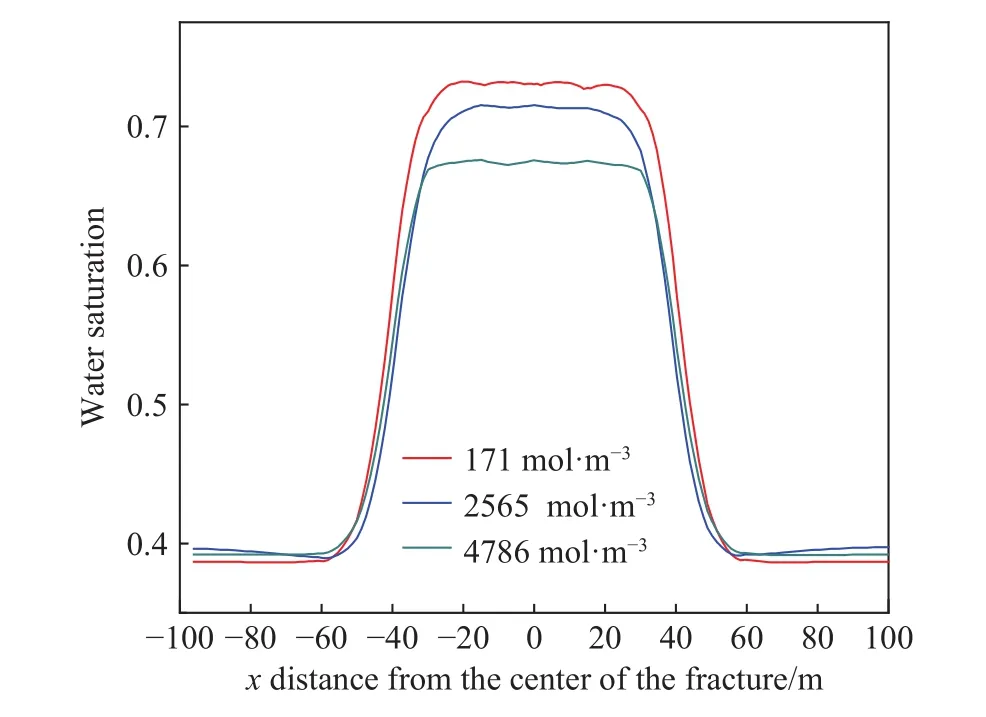
图16 关井后不同矿化度下的饱和度分布Fig.16 Distribution of saturation under various salinity levels

4.2.3 膜效率

页岩具有非理想半透膜，水分子可以自由通过半透膜，而压裂液中盐离子不能或者只能部分通过半透膜，Schlemmer等[35]测试发现页岩膜效率位于0.11～0.31之间，有些甚至低于0.1. 而膜效率会影响渗透压的大小，进而影响渗吸作用，所以选取膜效率为5%，15%，30%来探究其对渗吸效果的影响.

图17可以看出关井结束后，膜效率为5%和10%含水饱和度几乎相同，比膜效率为30%含水饱和度仅高出0.03，表明膜效率对渗吸影响不大.这是因为渗吸主要由压力主导，而页岩的非理想半透膜效应，进一步弱化了渗透压的驱动作用.

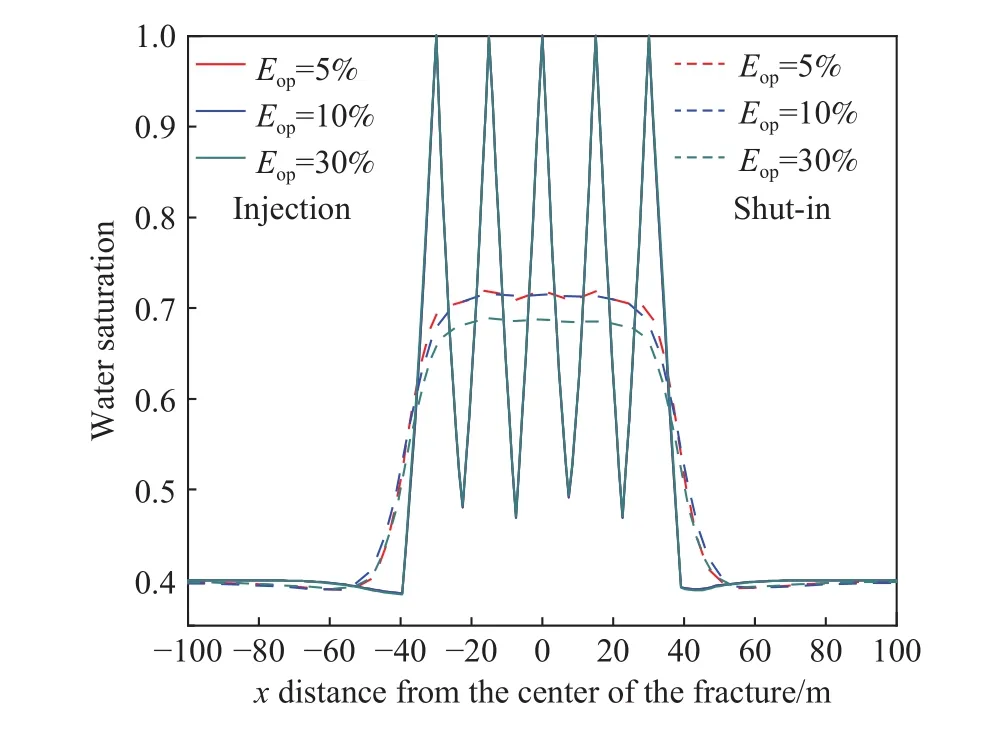
图17 不同膜效率下的饱和度分布Fig.17 Saturation distribution at various membrane efficiencies

图18为膜效率分别为5%、10%和30%时沿x轴方向的盐浓度变化，由于非理想半透膜的作用，膜效率越高，可以穿过半透膜的离子越多，所以裂缝处盐浓度越高.

图18 不同膜效率下的盐浓度分布Fig.18 Salt concentration at various membrane efficiencies

4.2.4 分支缝面积占比

图19对比了分支缝面积占比（Pbf）为0%（只包含主缝），30%，60%的含水饱和度和盐浓度剖面图，其中复杂裂缝与单一主缝相比，裂缝改造面积增加了30%，含水饱和度降低了0.008，对于复杂裂缝，分支缝面积占比60%与30%相比，含水饱和度降低0.003，这说明了在目前密切割压裂的背景下，裂缝复杂程度对渗吸效果的影响作用不明显，主要原因是簇间距小于压裂液的波及范围，所以分支缝的作用受限.

图19 不同分支缝面积占比的剖面图. （a）含水饱和度；（b）盐浓度Fig.19 Sectional views of various branch joint area proportions: (a) water saturation; (b) salt concentration

5 结论

（1）针对高黏土矿物含量的页岩储层中，滤失作用主要由压力差，毛管力和渗透压3种作为驱动力，在关井期间起着关键作用，其中压力差对滤失的影响最大.

（2）关井时间对压裂液的渗吸作用影响较大，前期渗吸作用明显大于后期，15 d的渗吸量达到了总渗吸量的80%左右，且关井压力扩散会波及到两侧压裂段. 关井50 d，发生渗吸的区域占据整个压裂段，这也是关井后返排初期产量与不关井相比较高的原因.

（3）当低盐度压裂液进入高盐度地层中时，盐浓度差越大，扩散速度越快，并且高盐度差会强化渗透压的渗吸效果，增加渗吸作用波及的范围，使裂缝处含水饱和度越低. 对于地层水矿化度为4.786×103mol·m-3的情况，裂缝附近的矿化度达到600 mol·m-3左右所需关井时间为50 d.

（4）页岩半透膜的膜效率对渗吸影响较小，膜效率30%与5%相比渗吸量增加4%. 这是由于地层中流体的流动主要由压力差主导，而页岩的非理想半透膜效应会进一步弱化渗透压的驱动作用.

（5）目前页岩油储层大多使用密切割压裂，由于簇间距小于注入压裂液的波及范围，关井后含水饱和度受小间距水力裂缝控制，分支缝对渗吸含水饱和度的影响有限.