四足机器人软硬地面稳定过渡的腿部主动变刚度调节策略

刘 帅，赵 慧，刘清宇✉

1) 武汉科技大学冶金装备及其控制教育部重点实验室，武汉 430081 2) 武汉科技大学机械传动与制造工程湖北省重点实验室，武汉 430081

相比传统的轮式和履带式，四足仿生机器人因腿部多关节构造及运动落足点离散等特点，理论上在非结构化的环境中具备优势[1]. 随着人工智能和接触动力学等专业领域研究的不断深入，四足机器人逐渐向智能化、柔性化和多样化的方向发展. 因此，在仓储物流、家庭娱乐、军事侦察和核电巡检等场合的应用前景广阔[2-4].

然而，多场景的使用也对机器人的运动控制性能提出了较高的要求. 众所周知，大陆地表形态各异，不仅有较硬质的沥青马路和塑胶跑道等人工路面，而且还存在着松软的草原等自然表面(地面的软硬概念表征其在受到外部压力作用时发生弹性形变的难易程度). 人和动物的足端在与地面接触过程中其关联腿部如同一个机械弹簧，而最简单的奔跑、跳跃模型可以利用弹簧负载倒立摆(Spring loaded inverted pendulum，SLIP)进行等效[5].当机器人在软硬程度不同的地面环境下运动时，足端也受到了地面大小不等的反作用力. 实验表明，人类和动物会根据足端所处地形的刚度调整自身腿部刚度的大小，处于柔软的表面上会增大腿部刚度，在坚硬的表面上则会减小腿部刚度，以此达到主动顺应的效果[6-7]. 同时，大量研究发现，变刚度腿部顺应性能够提高自主动态运行机器人移动速度和效率，以适应地形和有效载荷的变化[8-12].足式机器人在不同地面刚度环境中快速运行时，腿部刚度的及时调整对自身稳定性具有重要意义[13-14].

Bosworth等[15-16]进行了超级迷你猎豹(Super mini cheetah，SMC)机器人在软硬地面间的动态跳跃实验，通过原地测量地面阻抗和摩擦力提高了SMC在未知多变地形下的动态运动性能，发现从硬质到软性表面的过渡需要实时的地面特性测量和控制器的自适应. Miller等[17]提出了腿刚度控制策略，通过实时估计地面刚度并及时调整腿部刚度，成功实现了SLIP模型在地面刚度相差三个数量级的不同地面间的稳定过渡. 还有学者基于深度学习的方法对机器人足端与地面交互过程中的力和力矩数据进行了分类和归纳，通过新的聚类技术使机器人不仅能识别不同的地形，还能判定腿与相关地形之间的相互作用[18]. 但是，上述研究并未给出能及时有效调控机体姿态的理论或方法，特别是在面对突变地形的时候，机体偏转的情况是较为常见的，姿态角的误差一旦累积过量，容易导致整体重心不稳，出现倾覆的可能性大大增加.

目前，学界针对多变地形适应性问题，能有效调控运动姿态的理论主要有3种. 一种是基于零力矩点(Zero moment point，ZMP)的稳定性判据的方法[19]. 周坤等[20]基于此原理研究了爬行步态，通过机器人摆动腿的落地感知未知地形的高度、坡度等信息，实时控制各支撑腿长并用以调整质心高度和机身姿态，实现了在未知地形的自适应稳定行走. 但这种方法多应用在低速静步态的情况，机器人高速奔跑时往往是双足甚至单足支撑，无法满足判据中的支撑多边形的条件. 还有采用中枢模式发生器(Central pattern generator，CPG)的方法，借鉴动物的节律运动[21]. 韦中等[22-23]在此基础上采用仿生的脊柱结构，提出一种适用于粗糙可变地形的对角小跑运动控制策略，通过感知机器人本体状态和足端接触力对所规划的步态进行了调节. 基于CPG的方法通常需要一个复杂的非线性振荡器来建立控制器，并且对参数有很强的依赖性. 应用较为广泛的还有虚拟模型控制(Virtual model control，VMC)的方法. 这种方法认为机器人与环境的交互并非刚性，而是柔性连接，通过引入虚拟刚度、虚拟阻尼等概念对关节力矩进行分配，以此实现目标轨迹上的运动[24]. Ding等[25]基于虚拟模型控制和模型预测控制的思想，提出了一种适用于四足机器人在粗糙地形上行走的控制算法. 张国腾等[26]利用虚拟模型对四足机器人对角小跑步态进行了控制，并在仿真环境下实现了平地上的移动并跨越了不规则的地形环境. 难点在于该方法对比例、微分等参数的精确整定要求较高. 其他还有如谢惠祥等[27]采用支撑腿的侧摆关节力矩对机身姿态进行控制的方法，但这也容易引起额外的侧向运动，加剧机身振荡.

因此，本文为了解决机器人在变刚度地面行进过程中易出现的姿态角偏差的问题，力图在足端着地时采用合理有效的调节腿部刚度的方法对机身翻转量进行补偿，通过提出一种腿部主动变刚度调节策略，在着地时检测机身姿态的变化量，同时估计着地腿与地面的耦合刚度，根据前后两着地腿与所接触地面耦合刚度差，将差值补偿到相关支撑腿刚度计算公式中，得到的力矩用以驱动机器人各着地腿对应的膝关节转动，从而改变足端反作用力的大小，以此实现对机身姿态偏移纠正的目的，同时得到了更加适用于在软硬地面稳定过渡的控制策略.

1 对角双足支撑下的足-地耦合动力学

拥有腾空相的对角小跑步态高度对称并具有较快的速度，在马、狗等四足哺乳动物中常见. 本文对四足机器人以对角步态在软硬程度不同的变刚度地面间的过渡情形进行了研究. 当机器人以对角双足支撑着地时，由于支撑腿的前摆髋关节的反作用力导致机器人绕自身对角线发生偏转，机身姿态角会出现偏差. 如图1所示，机器人以对角步态在软硬程度不同的变刚度地面间进行跨越运动，此时，前腿(Front leg)和后腿(Hind leg)的足部会分别落在较软的前着地面(Front ground)和硬质的后着地面(Hind ground). 前腿支撑在软性地面，后腿支撑在硬质地面. 本文研究的重点在于其中一对支撑对角腿①、④对机体姿态的调节作用，因此将腾空的另外一对对角腿②、③并未画出.

图1 在变刚度地面上的姿态偏转Fig.1 Attitude deflection on the ground with variable stiffness

图1中，坐标系{GXYZ}是固定在地面的全局坐标系，坐标轴X的正向是机器人的水平前进方向，坐标轴Z的负向与地球重力加速度g的方向一致，采用右手定则确定第三个坐标轴Y的方向.L、m、J分别是机器人纵向体长、质量以及机身转动惯量；khard、ksoft、chard、csoft分别是硬质表面与软性表面的刚度和阻尼；kleg1、kleg4、cleg1、cleg4分别是前后腿①、④的足部到各自髋关节部分的等效虚拟弹簧腿的刚度和阻尼；θpitch、θ1(t)和θ4(t)分别是机身俯仰角以及前后虚拟弹簧腿的等效摆角；发生柔性接触的前后足端与各自所处表面可视为两个弹簧串联的物理等效模型. 于是可以得到，k1、k4、c1、c4分别是虚拟弹簧腿①、④与各自着地面的耦合刚度和耦合阻尼. 其中，耦合刚度k1、k4计算公式如下：

由式(1)、(2)可知，前后支撑的虚拟腿刚度一致时，若两着地面的地面刚度差异较大，前后腿的足-地耦合刚度也会随之不同.

机器人在此情况下的着地相运动方程为：

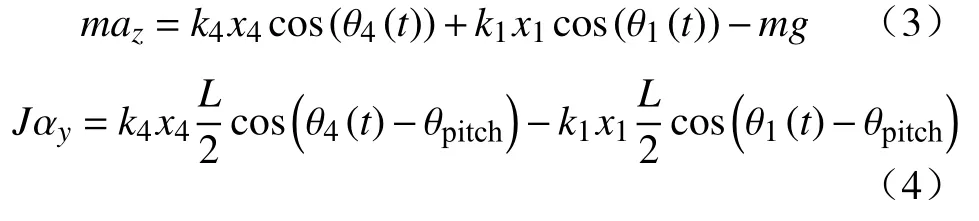
式(3)、(4)中，az、g分别是机器人质心加速度在垂直方向上的分量以及地球的重力加速度，αy是俯仰角加速度，其数值的测定采用了近似的思想，即俯仰角θpitch对时间的二阶导.x1、x4是前后支撑腿与各自着地面的等效压缩量. 由于两足端受到地面反作用力的不同，会造成等效压缩量存在区别，支撑腿长的不等导致机身出现翻滚，因此产生了姿态偏差的问题.

2 四足机器人腾空相控制

Raibert[28]教授针对足式机器人的动态运动，提出了著名的“三分法”解耦控制的理念，分别是前进速度、跳跃高度以及身体姿态.

对于前进速度的控制，机器人足端在腾空结束后的触地位置直接影响了后续着地状态下的加速度. 因此，为了达到使机器人加速或减速的目的，控制系统引入了不对称性，以调节前进速度大小，使其能从一种前进速度变化到另一种前进速度. 如图2所示，各个腿的序号依次是①、②、③、④，其中①、④互为对角腿，②、③是另一对.

图2 各腿序号Fig.2 Serial number of each leg

通过在腾空阶段规划落足点位置实现对前向速度控制. 即：

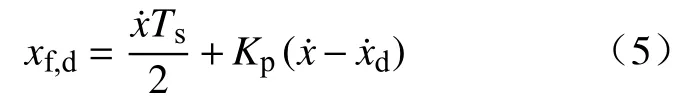
式中，xf,d为虚拟弹簧腿期望落足点位置，、d分别是机身的实际水平速度和期望水平速度，Kp为速度反馈增益，Ts是着地时间.

这里以单腿①为例，研究腾空腿关节力矩的作用，单腿示意图见图3所示.

图3 单腿示意图Fig.3 Diagram of one leg

图3中， τi1、 τi2、 τi3分别是第i条腿(i取1、2、3、4中的一个值)的侧摆髋关节、前摆髋关节和膝关节的驱动力矩；L1、L2、r1(t)分别为大腿(Thigh)、小腿(Calf)和单腿①的虚拟弹簧腿(Virtual spring leg)的长度； φi1、 φi2、 φi3、 θi(t)分别是第i条腿的侧摆髋关节角度、前摆髋关节角度、膝关节角度和等效摆角， γi是第i条腿的虚拟弹簧腿与自身小腿之间的夹角. φi1则由安装在侧摆关节处的角度传感器测量得到， φi2和 φi3可根据数学几何关系推出.以第①条腿为例，如式(6)、(7)所示：

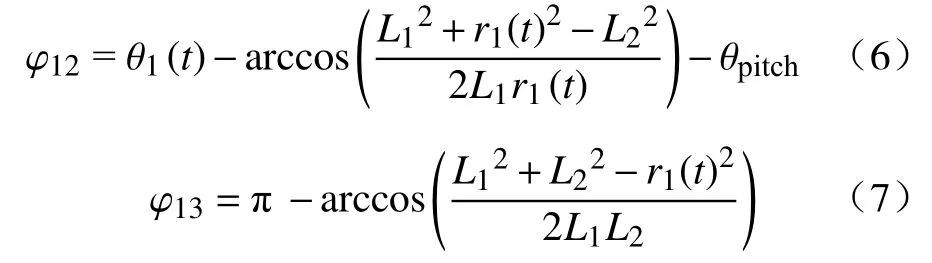
四条腿的运动状态以足-地接触力作为判定标准，引入有限状态机(Finite state machine，FSM)对各状态进行监控和条件转移. 基于位置控制的思想，利用多项式函数对腿部的目标摆动角进行规划，通过逆运动学求解得到对应的各个期望关节角(Desired joint angle,φD)，此数据与实时的关节角(Actual joint angle，φA)进行比较，得到的误差输入比例微分(Proportion differentiation，PD)控制器并进行及时处理，换算得到的力矩值作为电机参数，驱动机器人关节运动. 使其中一对对角腿(这里以腿①、④为例)以一定的角度触地. 落足点远离或接近中性点，机器人得到的净向前加速度，使整体加速或者减速，以便达到期望的水平速度. 同时，另外一对对角腿②、③摆动到合适的位置，为下一周期的着地状态做好准备，依次循环往复. 腾空相流程见图4.

图4 四足机器人腾空相控制Fig.4 Control of the quadruped robot in flight phase

3 四足机器人着地相控制

3.1 跳跃高度控制

机器人在着地过程中会进行跳跃高度与身体姿态的控制. 足端与地面的非弹性碰撞以及各关节运动阻尼等因素均会导致系统能量的损失. 为了保证四足机器人持续稳定运动，需要及时对其进行能量补充. 在忽略空气阻力影响的前提下，当机身下落到最低点时利用势能与动能之间的能量关系，计算得到相应的系统能量补偿值，这部分能量是通过对虚拟弹簧腿刚度的修正实现.

3.2 姿态控制

3.2.1 常规姿态反馈控制

影响四足机器人机身姿态偏差的因素不仅仅存在于对角着地的情况，还有外部难以避免的额外干扰、机器人自身结构的非对称性又或是腾空相摆动腿所产生的反作用力无法得到及时补偿等. 机体姿态偏移角的合理控制是实现机器人持续稳定运动的前提条件. 在腾空相，机器人的角动量守恒，为了解决在对角步态下产生的翻转问题，应选择在着地时采用一定的手段对姿态偏差进行纠正. 通常的解决办法是在足端着地时利用腿部的侧摆髋关节和前摆髋关节对机身施加相对应的反作用力用以纠正姿态角偏差，即常规姿态反馈控制(Conventional attitude feedback control，cAFC)：

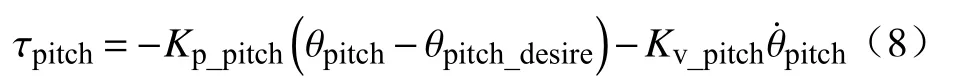
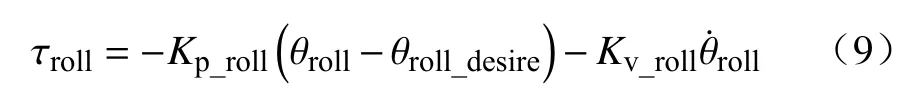
式(8)、(9)中，τpitch、τroll分别为机身俯仰角、滚转角调节力矩，Kp_pitch、Kp_roll 、Kv_pitch、Kv_roll分别是机身俯仰角和滚转角的位置和速度反馈增益，分别是机身俯仰角和滚转角以及相对应的俯仰角速度和滚转角速度，θpitch_desire、θ roll_desire是期望俯仰角和滚转角，一般设置为0.

3.2.2 主动变刚度调节策略

这里提出一种新的姿态调控方案.

令Δk=k4-k1，代入式 (3)、(4)中，整理得：

由式(10)、(11)联立求解得到：

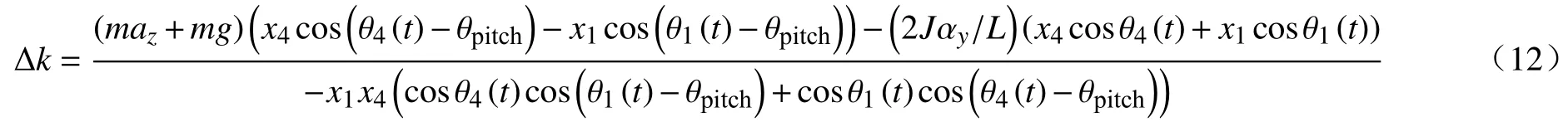
其中，等效压缩量x1、x4计算公式分别为：

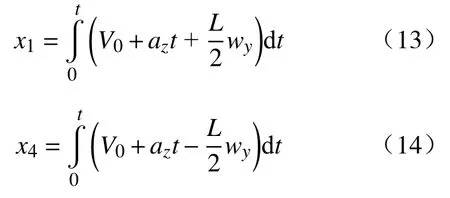
式(13)、(14)中积分下限为当前步态周期下四足机器人对角双足刚触地时的时刻，积分上限为着地过程中的任意时刻. 考虑到等效压缩量x1、x4在整个着地阶段不断变化，因此，以刚触地的时刻作为上述积分的“零时刻”，之后的着地过程中积分上限值t便是相对于该“零时刻”的时间. 换言之，从对角腿着地瞬间开始，等效压缩量就已经进行计算.V0是机器人在当前步态周期刚着地时的机身质心垂直方向的速度分量.wy是机身的俯仰角速度. 着地过程中，腿部会受到地面反作用力，这个力又作用于机身，使得机身得到一个竖直方向的加速度az.

从上一周期下落至最低点到足端离地的时间内，以下落至最低点的时刻作为积分下限，以离地腾空瞬间的时刻作为积分上限，对机身竖直方向的加速度az进行积分可以得到上一步态周期离地瞬时的垂直速度. 离地开始腾空后，忽略空气阻力等外部因素的影响，此时机器人整体只受到自身重力的影响，上一周期离地到当前周期着地的时间差与重力加速度g的乘积便可得到当前周期着地时刻与上一周期离地时刻的速度变化量，从而得到V0：

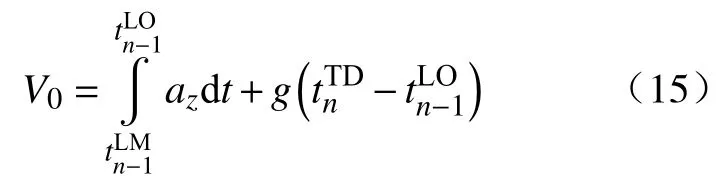
将计算得到的x1、x4和其他可测量值代入公式(12)中，得到等效刚度变化量 Δk.

3.2.3 着地腿关节力矩设置

在着地相，机身的滚转姿态调整是利用常规姿态反馈控制实现，通过施加力矩 τ11、 τ41在相应对角着地腿的侧摆髋关节上. 其中：

俯仰姿态调整则有所不同，在着地相时，对角着地腿的前摆髋关节力矩值 τ12、 τ42使之为0. 即：

通过对角着地腿的膝关节力矩来对机身姿态施加影响. 将公式(8)中常规姿态反馈控制方法得到的俯仰角调节力矩 τpitch转换为前后着地腿力的差值 ΔF：

以图1所示情况为例，着地腿①、④沿虚拟等效腿的方向上的力分别为：

式(19)、(20)中，kregister是三分法中为保证四足机器人跳跃到目标高度，由能量关系计算得到的腿部刚度补偿量，在机身下落到最低点时添加到沿虚拟等效腿的方向上的力的计算表达式中，r0是等效弹簧腿的初始长度，分别为着地腿①、④的实时腿长及其变化率.

结合常规姿态反馈和主动变刚度调节策略得到沿虚拟弹簧腿的方向上的力，其计算表达式为：

两着地腿①、④的膝关节驱动力矩 τ13、 τ43如下：

将计算得到的侧摆髋关节力矩、前后摆髋关节力矩以及膝关节力矩值输入到关节力矩指令控制器中，驱动各关节的运动. 需要注意的是，用于姿态调控的关节力矩从对角腿触地就开始施加，而用于高度控制的虚拟腿刚度补偿量kregister只会在机身下落到最低点才会增加到公式(19)、(20)中，在着地的其他时间段内kregister视为0. 足端对腿部产生的力反作用于机身，使机身在侧向和俯仰方向的姿态偏移量得以纠正，从而实现对机器人着地相控制.

对于身体姿态的调整，本文提出采用腿部主动变刚度调节策略(Active and variable stiffness adjustment strategy for legs，aVSL)与常规姿态反馈控 制 (Conventional attitude feedback control，cAFC)相结合的方法. 通过传感器和陀螺仪测得机身高度、角度等信息，将腿地耦合过程中的刚度差通过主动变刚度调整策略补偿到着地腿中，并在着地阶段增加常规姿态反馈控制作为腿部主动变刚度调节策略的补偿，以此期望达到更好的姿态控制效果. 相关控制流程如图5所示.

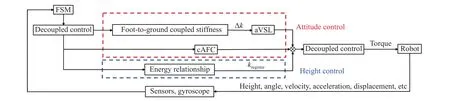
图5 四足机器人着地相控制Fig.5 Control of the quadruped robot on the ground

4 四足机器人对角小跑仿真平台

四足机器人对角小跑仿真平台的搭建采用Simulink-SimMechanics模块，SimMechanics为多体动力机械系统及其控制提供了直观有效的建模分析手段，一切工作均在Simulink环境中完成，避免了多种软件联合仿真交互过程中容易产生的不兼容问题.

如图6所示，四足机器人整机模型共12个关节，单腿由髋关节(包括前摆和侧摆两个转动关节)、膝关节、足部以及大小腿等组成. 机身形状设置为长方体，髋关节形状是球体，膝关节为圆柱体，足端的形状为球体.

图6 三维实体模型Fig.6 Three-dimensional solid model

仿真模型中有关初始速度、关节角度等重要参数设置则可见表1所示.

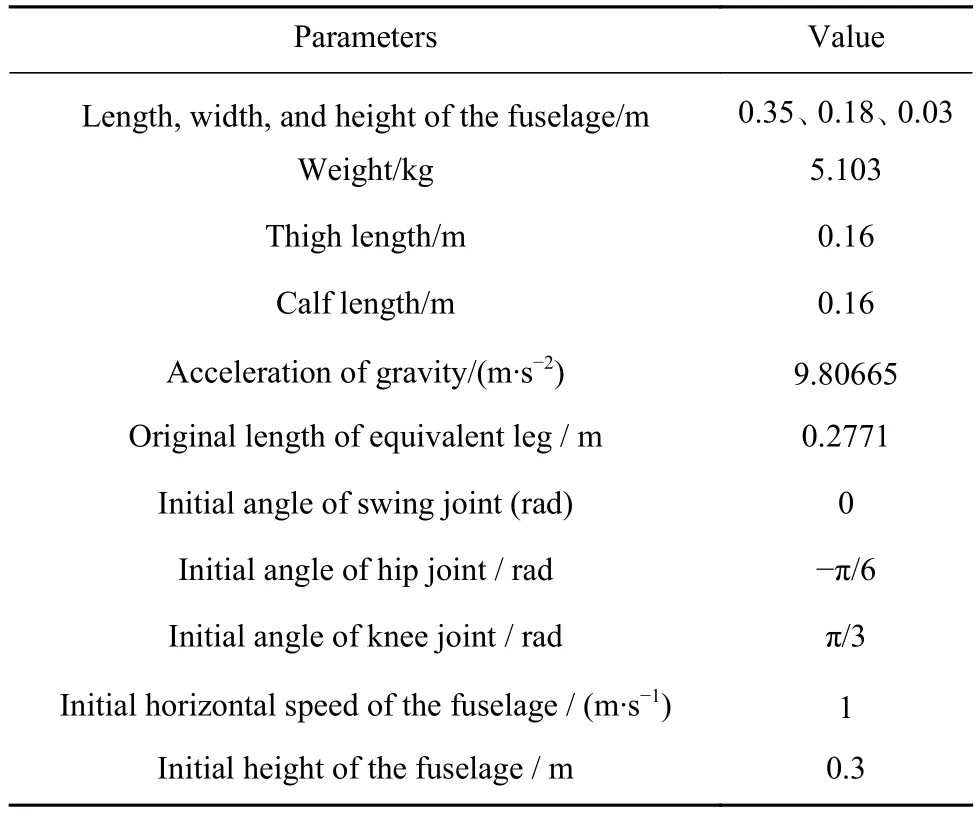
表1 模型的重要参数Table 1 Important parameters of the model

5 仿真实验结果对比与分析

5.1 同一刚度地面下四足机器人对角小跑姿态控制

为了验证常规姿态反馈对于四足机器人对角小跑姿态偏转的调控效果，这里将落地面刚度和阻尼分别设定为 107N·m-1和 2000 N·s·m-1的环境，保持各腿部的虚拟刚度为2000 N·m-1. 一个重约5.103 kg的四足机器人以1 m·s-1的水平初速度从离地0.3 m高的位置开始进行对角双足着地支撑运动. 仿真视频截图如图7所示.

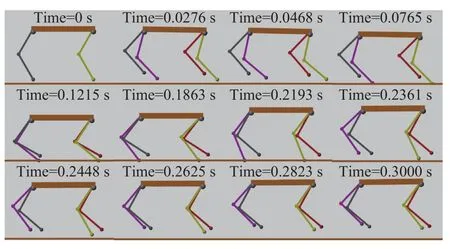
图7 仿真视频截图Fig.7 Screenshot of the simulation video

仿真平台的存储模块记录了各个腿部的足端随时间变化的运动状态(腾空或着地)，见图8. 其中，状态标记值(State)为0时表示着地相，状态标记值为1表示腾空相. 由此可以看出在0到0.0764 s的时间段内，腿①、④处于腾空相，而0.0764 s到0.2192 s的时间段内，腿①、④处于压缩与起跳的着地相，0.2193 s后腿①、④离地重新进入腾空相.仿真时间内，腿②、③一直处于腾空相，未与地面接触.

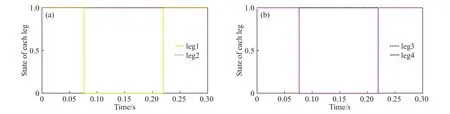
图8 腿部状态. (a) 腿 1、2 状态; (b) 腿 3、4 状态Fig.8 State of each leg: (a) states of the first and second legs; (b) states of the third and fourth legs

结合运动状态相图和图9的机身侧向运动变化曲线可以获知，腾空相时的机身滚转角接近于0，在①、④着地压缩阶段，滚转角有一定的负向增大，最大值为-0.00865 rad(≈-0.4956°)，同时机身质心的侧向位移也在增大，最大值约为5×10-4m. 当进入着地相起飞阶段后，通过常规姿态反馈一定时间的作用，机身的滚转偏移量逐渐减小，并在离地时刻 (Time：0.2193 s)调整到 0.001 rad(≈0.0573°)，并且侧向位移也减小到0值附近，这是在一个可以接受的范围内. 离地后摆动腿的力矩干扰等因素，其俯仰角又开始有所增大，需要在下一周期的着地阶段进行控制.

图9 机身侧向运动. (a) 机身侧向位移; (b) 机身滚转角; (c) 机身滚转角速度Fig.9 Lateral movement of the fuselage: (a) lateral displacement of the fuselage; (b) roll angle of the fuselage; (c) roll angular velocity of the fuselage

图10为机身俯仰运动变化曲线，俯仰偏移在四足腾空相时较为明显，最大值达到-0.0235 rad(≈-1.3465°)，通过在着地相对角腿腿力补偿的方式，俯仰角及角速度逐渐减小并稳定，离地时已恢复到0值附近. 可以看出，对于同一刚度地面下的对角双足支撑，在着地相时利用常规姿态反馈控制的方法是可以稳定机身姿态的.

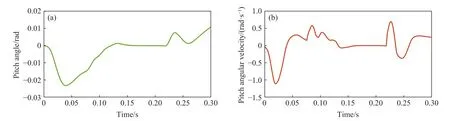
图10 机身俯仰运动. (a) 机身俯仰角; (b) 机身俯仰角速度Fig.10 Pitching motion of the fuselage: (a) pitch angle of the fuselage; (b) pitch angular velocity of the fuselage

因此，当四足机器人在同一刚度的水平地面上进行对角步态运动，在着地相的对角双足支撑过程中，常规姿态反馈对机身俯仰和滚转姿态偏斜可以起到有效的控制作用.

5.2 变刚度地面下四足机器人对角双足支撑时姿态控制

当两对角腿各自落足点处于不同刚度的表面上，即较硬质表面(khard和chard分别是107N·m-1、2000 N·s·m-1)和 较 软 性 表 面 (ksoft和csoft分 别 是2×104N·m-1、20 N·s·m-1). 在着地相期间分别进行常规姿态反馈、常规姿态反馈与主动变刚度调节策略对机身姿态进行联合调控的仿真对比实验.得到的仿真视频截图如图11、12所示.

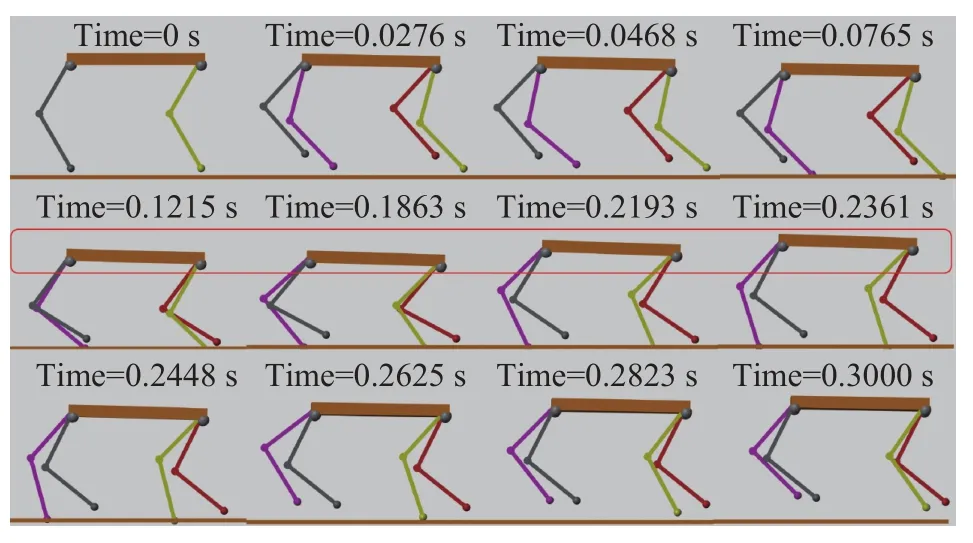
图11 变刚度地面下单独采用cAFC的仿真视频截图Fig.11 Simulation video screenshot of the cAFC alone under the ground with variable stiffness

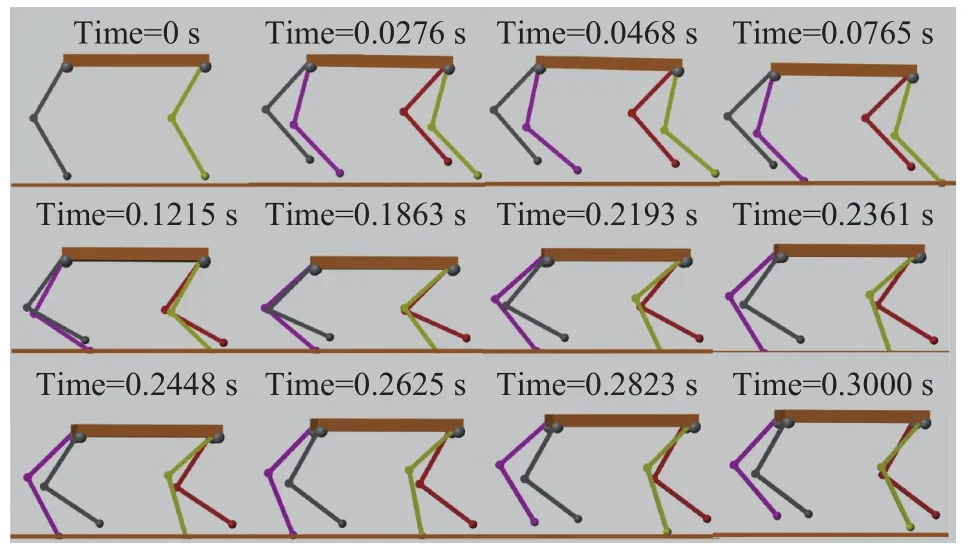
图12 变刚度地面下cAFC与aVSL联合作用的仿真视频截图Fig.12 Simulation video screenshot of the combined action of cAFC and aVSL under the ground with variable stiffness

变刚度地面下的机身侧向滚转姿态变化曲线如图13所示，在0到0.0764 s的时间段内，机器人处于腾空相，腿部的摆动对机身侧向运动的影响可忽略不计. ①、④腿着地后，对角双足支撑在两地面刚度差异较大的环境下，在仅仅采用常规姿态反馈进行控制时，机身滚转角偏差有明显的增大趋势，在 0.3 s时达到-0.027 rad(≈-1.547°). 而在作为对照组的常规姿态反馈与主动变刚度调节策略联合调控机制下，滚转角及其角速度曲线虽然在着地后的短时间内发生了一定的波动，但这是因为对于滚转角的控制依然是基于常规姿态反馈的方法，而当腿部施加以主动变刚度调节策略后，着地腿的腿力补偿较快，关节力矩的变化在较短时间内完成，导致机身侧向姿态出现了明显改变，然后，通过常规姿态反馈的方法，机身滚转姿态偏移量逐渐得以补偿，并在0.15 s时，机身的滚转角速度减小到仅为 0.1 rad·s-1(≈5.73°·s-1)，并稳定在这一值附近，直至足端在下一周期离地腾空. 由此说明，对角落足点在两个刚度相差较大的地面上运动时，仅采用常规姿态反馈对侧向姿态的调控作用并不理想，而当常规姿态反馈控制与主动变刚度调节策略联合时取得了更好的作用效果.

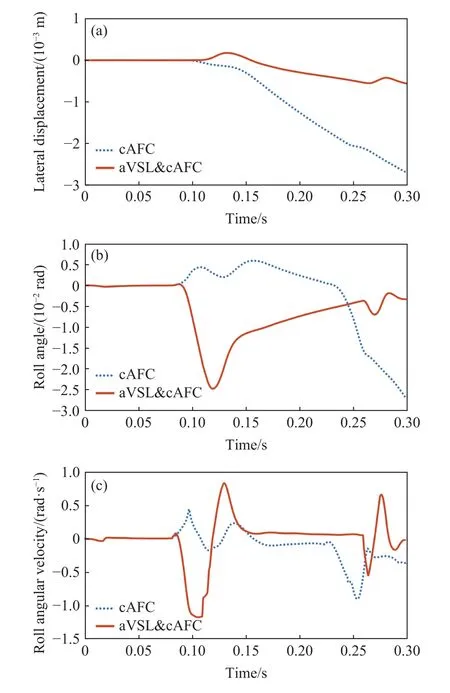
图13 变刚度地面下的侧向运动. (a) 变刚度地面下的侧向位移; (b)变刚度地面下的机身滚转角; (c) 变刚度地面下的机身滚转角速度Fig.13 Lateral motion under the ground with variable stiffness: (a)lateral displacement under the ground with variable stiffness; (b) roll angle under the ground with variable stiffness; (c) roll angular velocity under the ground with variable stiffness

变刚度地面下的机身俯仰姿态变化曲线如图14所示. 对于机体俯仰姿态控制，姿态调整发生在着地相，因此未施加主动变刚度调节策略和施加主动变刚度调节策略的机身俯仰角及角速度曲线变化与腾空相是一致的. 在着地瞬间机身的俯仰角约为-0.015 rad(≈-0.859°). 在未施加主动变刚度调节策略时，机身俯仰姿态变化曲线波动明显，0.2155 s时俯仰角最大值为-0.033 rad(≈-1.891°)，离地瞬间(Time：0.2448 s)的俯仰角为-0.0279 rad(≈-1.5986°). 作为对照组，施加主动变刚度调节策略时，俯仰角速度变化曲线在着地过程较为平滑.同时，因为对软性地面着地的等效腿施加了刚度补偿，对角腿的腿力差作为机身关节力矩输入，使得俯仰姿态偏差得到了较好的调整，离地时机体的俯仰角为-0.004 rad(≈-0.2292°)，这是一个可以接受的值.

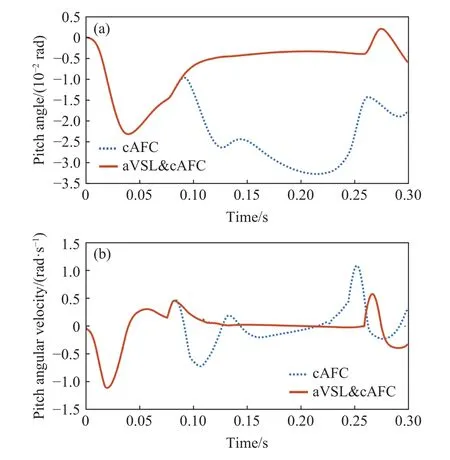
图14 变刚度地面下的机身俯仰运动. (a) 变刚度地面下的机身俯仰角; (b) 变刚度地面下的机身俯仰角速度Fig.14 Pitching motion under the ground with variable stiffness: (a)pitch angle under the ground with variable stiffness; (b) pitch angular velocity under the ground with variable stiffness

综合上述实验数据对比与分析，可以得出，当四足机器人以对角步态在两地面刚度相差较大的环境下过渡时，仅仅通过常规姿态反馈难以对机身姿态偏移量得到理想的调控效果，利用腿部主动变刚度调节策略并加以常规姿态反馈控制作为补充的方法，在侧向滚转姿态得以稳定的前提下，俯仰姿态的平衡控制取得了较好的实验效果.

6 结论

针对四足机器人在变刚度地面过渡时易出现姿态不稳定的问题，本文提出了一种基于足-地耦合动力学运动方程推导得到的腿部主动变刚度调整策略，通过仿真结果对比与分析，发现与仅利用常规姿态反馈控制方法相比，该策略与常规姿态反馈控制相结合的方式使机身俯仰姿态取得了更好的控制效果，同时能够保证机身侧向滚转姿态保持在一定的误差范围内. 该方法不需要对机器人实际关节进行结构性的改变，避免了整体冗余，对于对角小跑等动步态也能实现调整过程的自适应.

然而，对该策略的效果验证目前依然停留在仿真环境下，缺乏对现实情况下的实验测试，因此下一步是搭建物理样机，对所提控制策略进行真实变刚度地形下的四足机器人姿态控制实验，期望能得到更具说服力的结果.