降雨和地震条件下浅层黄土滑坡三维稳定性评价

李泊良，张帆宇

兰州大学土木工程与力学学院, 兰州 730000

黄土遇水和加载下，极易发生结构性崩塌和强度降低，导致黄土滑坡广泛分布且频发. 统计数据显示，我国有1/3的滑坡灾害发生在黄土地区，已经造成大量的人员伤亡和财产损失[1-2]. 降雨和地震是浅层黄土滑坡最常见的诱因. 降雨在黄土高原诱发了大量浅层黄土滑坡，诸如兰州、天水、宝鸡等地主要是降雨型滑坡[3-6]. 然而，这些地区还是历史地震的高发区和强影响区[7]. 诸如1718年甘肃通渭地震、1920年宁夏海原地震、1995年甘肃永登地震都引起了大量的黄土滑坡[8-10]. 作为滑坡的两大重要的诱因，两者耦合作用下能诱发更大范围、更广分布、更强破坏的黄土滑坡事件. 近年来，这类灾害链效应在黄土高原已有发生. 2013年天水持续降雨诱发大量浅层黄土滑坡后，该地区又突遇7.22彰县岷县6.6级地震. 震后调查显示诱发以浅层黄土滑坡为主的斜坡灾害2000多处[11-12].已有研究表明，震前的极端降雨事件会严重加剧同震滑坡的发生概率和灾害程度[13-16]. 因此，加强降雨和地震耦合效应下滑坡灾害的评价，对于不同尺度滑坡的防灾、减灾、应急都具有重要的指导作用. 然而，这类研究在黄土高原滑坡灾害评价中仍不多见.

滑坡灾害危险评价通常包括定性和定量两类方法. 定性方法主要是基于研究区地质条件和专家的经验对滑坡进行评级，而定量方法是依据物理模型和数学模型对滑坡进行分析[17]. 定性方法依赖专家的主观性，缺少重复性. 尽管定量方法可不同程度消除主观性的影响，且具有更好的适用性，但是需要大量数据的支持和输入. 尽管如此，定量方法已成为滑坡灾害评价中主要的方法[18].在各类定量评价的技术中，基于数字高程模型并结合岩土力学参数的确定性模型，已成为流域尺度滑坡灾害评价的重要方法.

物理确定性模型是通过无限斜坡稳定性模型，计算不同水文条件下的坡体稳定性，通常能获得准确客观的结果[17-19]. 根据计算斜坡的维度，可分为二维和三维确定性模型. 目前大多数确定性模型都是基于二维无限斜坡模型评估斜坡稳定性，常见的有基于区域栅格的瞬时降雨入渗的TRIGRS与考虑稳态水文分布的SHALSTAB[20-22].这些模型均可模拟降雨过程中土体中水的渗流场，评估降雨条件下斜坡的稳定性. 尽管这些二维确定性模型能一定程度考虑地质条件、水文条件和气候条件，还可较为准确预测滑坡稳定性，但是在计算过程中他们不考虑滑动面的方向，只假设滑动体沿坡体方向移动，这与实际情况不完全相同[23]. 为了弥补这些二维确定性模型存在的不足，有学者指出三维模型得到的预测结果能更符合实际情况. 例如Bromhead等[24]指出二维模型很难准确地表示岩土性质、地下水条件的空间变化和滑动面的形状，三维模型则能更准确的表示这些条件. 此外，Xie等[25]指出三维模型得出的结果要比二维方法更可靠. 因此，三维确定性模型当前成为滑坡稳定性评价中更为关注的方法.

Scoops3D是美国地质勘探局开发的三维确定性模型，用来评价和预测研究区内每个栅格的稳定性[26]. 目前，Scoops3D已经成功预测了沿海地区火山灰地层的滑坡稳定性[26]. 而黄土地层和火山灰地层具有一定的相似性，所以考虑利用该模型评价黄土滑坡的稳定性. 此外，该模型还可将其他水文模拟软件输出结果作为直接参数输入，具有将区域复杂水文条件耦合到稳定性评级模型中的优势[27]. Tran等[28]应用TRIGRS计算降雨过程中斜坡动态水文条件并输入到Scoops3D，对韩国Umyeon山区进行降雨条件下的稳定性评价，实现了降雨诱发滑坡的实时早期预警. Scoops3D模型还引入了水平地震加速度系数，用来计算地震条件下的滑坡稳定性. 因此，采用Scoops3D三维确定模型耦合降雨和地震条件，进而评价黄土地区的滑坡稳定性.

本文首先介绍了TRIGRS模型和Scoops3D模型的基本原理，并分析了模型各类参数在稳定性评价中的敏感性. 然后，选择兰州市大沙沟流域作为研究对象，结合TRIGRS和Scoops3D评价降雨、地震和两者耦合条件下区内浅层黄土滑坡的稳定性. 最后，结合滑坡点分布图，用混淆矩阵法和受试者工作特征（ROC）曲线法对预测结果进行评价，检验了降雨与地震触因及其耦合条件下对黄土高原流域尺度黄土滑坡稳定性评价结果的适用性.

1 模型方法

1.1 降雨渗透场模拟

TRIGRS模型是一种基于栅格数据计算降雨入渗的斜坡稳定性模型，该程序能计算降雨入渗引起的孔隙水压力变化以及随之变化的安全系数[20]. 该模型结合降雨入渗和地表径流的方法计算饱和与非饱和条件下的一维垂向渗流过程，能够获得降雨过程中土体压力水头和含水率的空间分布规律. 本文采用了降雨入渗的非饱和无限斜坡模型，在计算过程中将基底面以上的土体分为非饱和区和毛细饱和区，并通过Richards方程计算降雨过程中压力水头空间分布. Alvioli等[29]开发的TRIGRS 2.1提供了输出空间分布的孔隙水压力和体积含水量的功能，并可直接输入到Scoops3D模型使用.

1.2 Scoops3D模型

Scoops3D模型由美国地质勘探局开发，是基于数字高程模型，通过三维简化毕肖普法计算各滑动面上的栅格安全系数[26]. 该模型最初是为了评估火山灰地层中的滑坡稳定性，在尼加拉瓜的卡西塔和圣克里斯托瓦尔火山等多个地点进行了成功测试[26]. 随后还应用到华盛顿等区域的滑坡稳定性评价中，结果显示也具有较好效果[27].

Scoops3D通过圆弧检索法定义滑动面，模型根据检索参数定义若干检索点，以每个检索点为球心绘制半径递增的球体，球体与数字高程模型相交，相交面定义为滑动面,如图1所示.

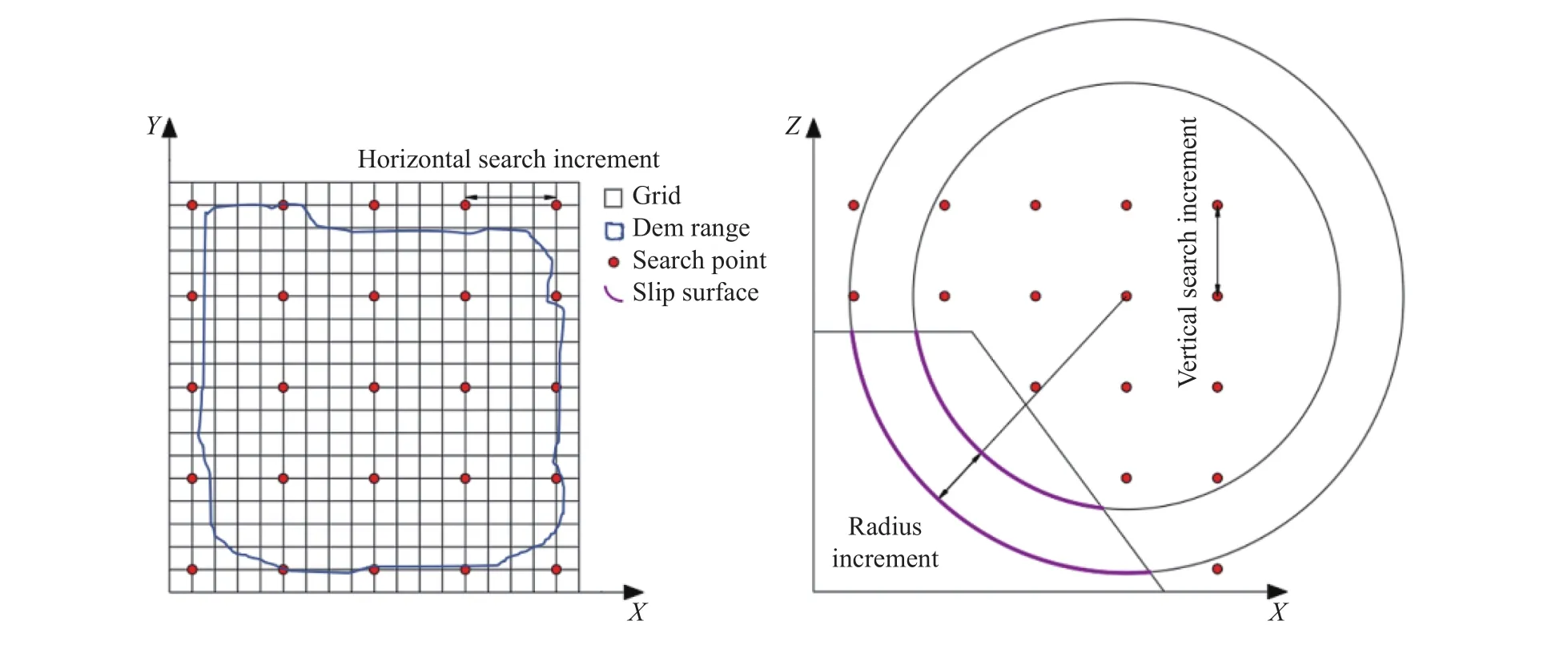
图1 Scoops3D检索原理图Fig.1 Retrieval principle of Scoops3D

在该模型的弯矩平衡法中，安全系数可以表示为抗剪强度s与剪应力τ之比，安全系数越大则滑块越稳定，安全系数计算如下式

土体的抗剪强度s通过摩尔库伦准则计算：

式中，c为土的黏聚力，φ为土的内摩擦角，σn为滑动体受到的正应力，u为切面的孔隙水压力.

Scoops3D稳定性模型对地震荷载是通过定义水平地震加速度系数Keq实现的，被视为作用在滑动体上WKeq的水平力. 根据单元栅格内滑动体受力矩平衡（图2），重力W、地震荷载WKeq、切向力S=τA对于球心产生的力矩和为0，e为球心到滑体重心的垂直距离，其余参数已在示意图中标出：

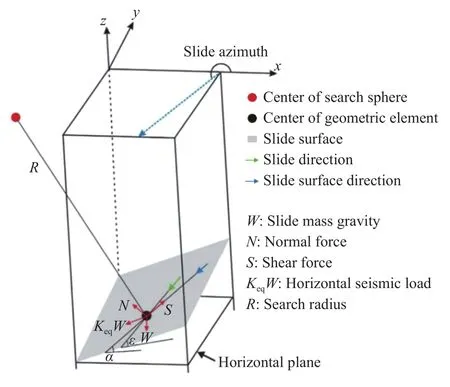
图2 单元栅格示意图Fig.2 Schematic diagram of cell grid

根据垂直方向的力平衡，重力W、法向力N=σnA的垂向分力、切向力S的垂向分力的合力为0：

通过式（3）和式（4）求解剪应力τ和正应力σn，带入式（2）和式（1）整理后得到三维稳定性系数计算公式：

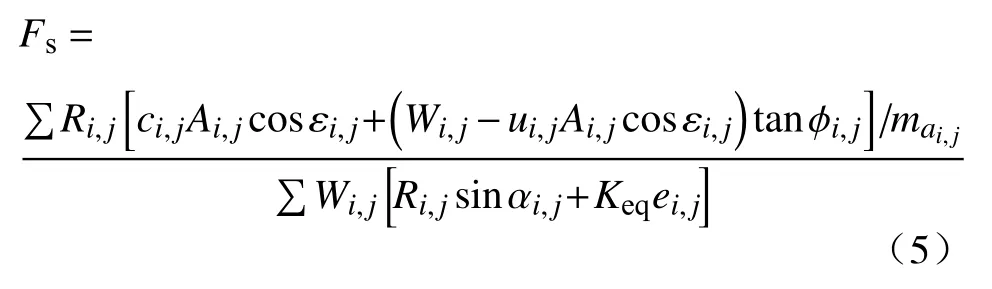
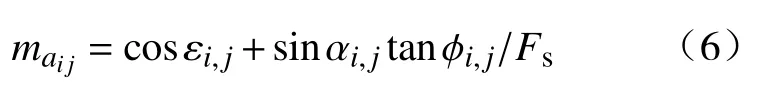
模型输入参数敏感性分析可直接地反映各参数对模型影响程度的大小，从而确定每个参数的重要性[30]. 本文基于稳定性系数计算公式，开展参数的敏感性分析，目的是分析各输入参数对Scoops3D模型影响程度程度，更重要的是指导在试验测试基础上确定输入参数的取值. 根据研究区的实际地层分布和试验测试的结果，确定了输入参数的标准值和取值范围（表1），保持其他参数为标准值，在取值范围内改变待分析参数，得到系数变化率，得到Fs对输入变量的相对敏感性变化规律（图 3）.

表1 敏感性分析参数变化范围Table 1 Variation range of sensitivity analysis parameters

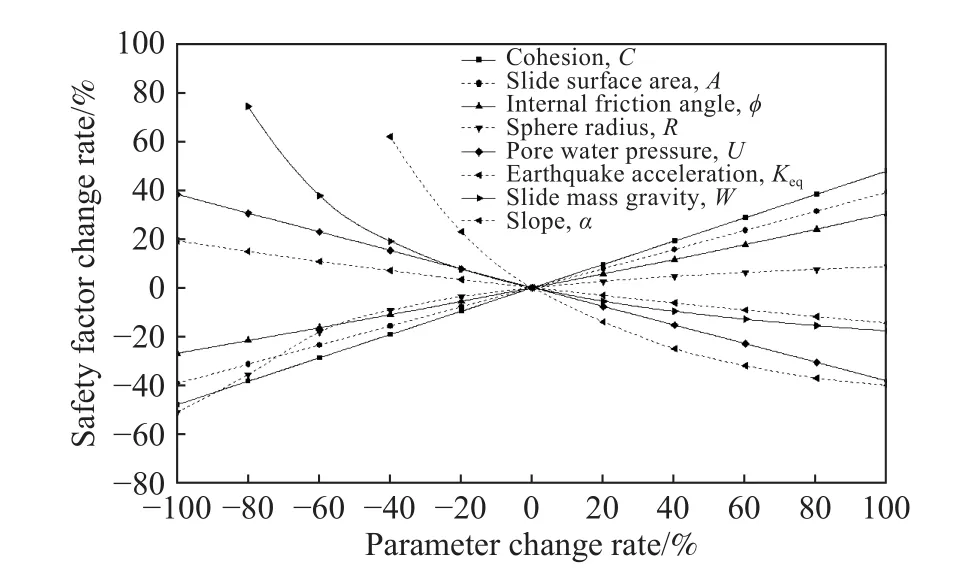
图3 参数敏感性分析结果Fig.3 Sensitivity analysis results of parameter

安全系数随黏聚力、内摩擦角、滑动面面积、球体半径、坡度的增大而增大，随地震加速度、孔隙水压力、滑块重量的增大而减小，这表明地形地貌和土体性质共同控制着斜坡稳定性（图3）. 在土体性质和地形条件基本确定的情况下，孔隙水压力和地震加速度在更大程度的控制斜坡的稳定性. 而降雨和地震也是触发滑坡最常见的要素. 因此，下文重点分析了研究区降雨、地震及两者耦合条件下斜坡的稳定性.

2 研究区概况

选择甘肃省兰州市大沙沟流域作为研究区.它处于黄土高原，地貌单元复杂，坡体坡度在0°到61°之间，海拔在1575 m到2023 m之间，区域面积100 km2. 研究区属于半干旱气候，平均年降水为293.3 mm，降雨主要集中在7～9月. 研究区出露地层主要为第四系马兰黄土. 研究区内新构造运动较为强烈，以垂直升降运动为主，具有明显的继承性、差异性特点. 基于1∶5000地形图，通过详细的现场调查和GPS现场测量，绘制了61处浅层滑坡点，如图4. 根据王恭先滑坡滑动面分类标准[31]，这些滑坡厚度均小于10 m，属于浅层黄土滑坡. 据历史地震资料记载，兰州市历史上曾多次遭到地震破坏，地震基本烈度为Ⅷ度，地震动峰值加速度系数为0.2[32].

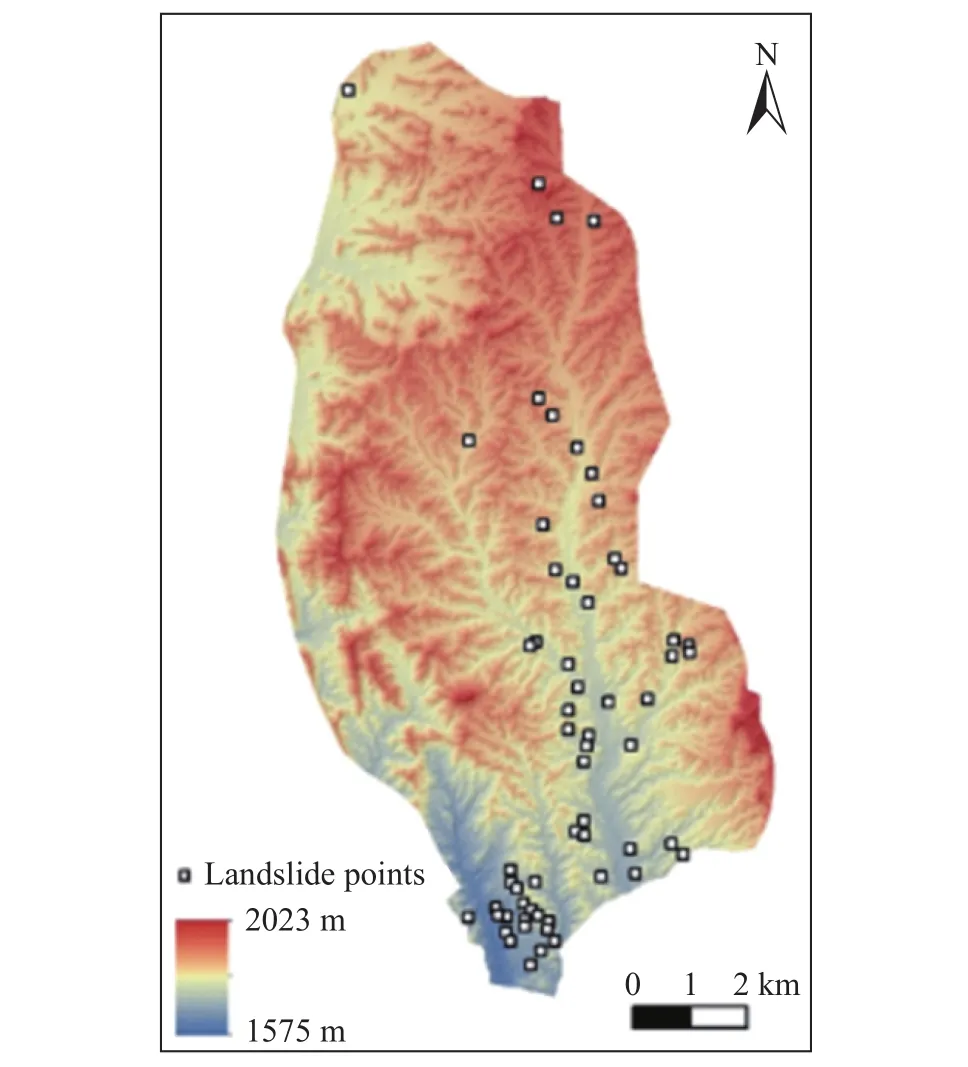
图4 研究区的数字高程模型和滑坡分布图Fig.4 Study area digital elevation model and landslide distribution map

3 材料和方法

3.1 数据和参数

Scoops3D模型和TRIGRS需要研究区的强度参数，本文参考了Wen和Yan[33]对马兰黄土强度的研究，两个模型所需的黄土参数设置如下表2.

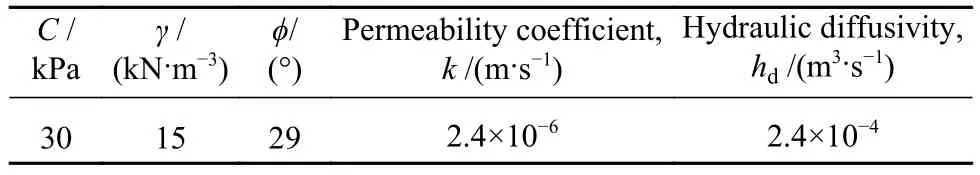
表2 土参数取值表Table 2 Soil parameter value table

降雨增加土体含水量，从而降低土体强度，斜坡稳定性随之降低. 土的抗剪强度在斜坡中起着重要作用，而非饱和黄土的基质吸力对抗剪强度有重要影响，Scoops3D中通过含水率与土水特征曲线共同计算基质吸力，然后计算非饱和土的抗剪强度. 本文用Fredlund和Xing的土水特征曲线模型（F-X）[34]对实测数据进行拟合，图5为土水特征曲线结果和F-X曲线参数，其中θs为饱和含水率，θr为残余含水率，α为进气值，n和m为曲线的形状参数.

图5 土水特征曲线图Fig.5 Soil water characteristic curve

TRIGRS和Scoops3D计算需要研究区的数字高程模型. Scoops3D对不同分辨率数字高程模型数据的预测结果存在差别，高分辨率数字高程模型显示的地貌更加接近真实环境，预测结果的准确性也随之提升. 已有研究发现，5 m以上分辨率的数字高程模型可以得到准确的结果，然而程度不显著，但是会显著增加计算量[35]. 因此，本文利用5 m分辨率的数字高程模型，结合绘制的滑坡点进行研究区的斜坡稳定性评价.

3.2 评价方案

本文首先利用TRIGRS渗流场模型计算体积含水率的空间分布规律，结合Scoops3D模型进行研究区斜坡稳定性评价，并分别评价了降雨、地震、及降雨与地震耦合条件下的斜坡稳定性. 结合气象局对降雨强度的分级标准，本文选择天然情况（无降雨），中雨情况（日降雨量25 mm，降雨时长24 h），暴雨情况（日降雨量100 mm，降雨时长24 h）3种方案分别对研究区进行斜坡稳定性评价. 研究区地震基本烈度为Ⅷ度，地震动峰值加速度系数为0.2. 本文评价地震加速度系数Keq在0～0.2范围内变化时研究区的稳定性情况. 最后结合降雨和地震的耦合条件，评价研究区的斜坡稳定性.

通过Scoops3D确定性模型得出各种条件下研究区各栅格的安全系数，本文按照安全系数的大小将稳定性等级分为4个等级，即不稳定区（Fs＜1.00），基本稳定区（1.00≤Fs＜1.25），稳定区（1.25≤Fs＜1.50），极稳定区（1.50≤Fs）. 随后使用GIS软件对结果进行统计和分析，最后用ROC曲线法和混淆矩阵法对各种条件下的预测结果进行评价.

4 结果与讨论

4.1 降雨作用下的稳定性评价结果

降雨是诱发浅层黄土滑坡的关键因素. 根据已有数据得到不同降雨条件下的稳定性评价结果（图6）. 无降雨条件下失稳面积为0.20 km2，中雨条件下失稳面积为1.33 km2，暴雨条件下失稳面积为5.35 km2. 根据图6（a）可发现无雨条件下的研究区的斜坡稳定性较好. 降雨发生后，大量斜坡在降雨入渗的作用下出现失稳现象. 预测结果显示降雨触发的浅层滑坡大多处于沟谷区域，中雨触发的滑坡面积是无雨状态的6.65倍，暴雨触发的滑坡面积是无雨状态的26.75倍. 可见，随着降雨量的增加，滑坡发生的区域呈现增加的趋势，这与其他学者得出的结论相吻合[28]. 研究区半干旱气候导致天然黄土多数处于非饱和状态，但当降雨发生后，随着降雨的入渗越来越多的黄土处于饱和或接近饱和的状态，高含水率的黄土抗剪强度显著降低，黄土斜坡的稳定性也随之降低. 结合敏感性分析结果，TRIGRS与Scoops3D的组合能考虑到降雨入渗会增加滑动体质量和孔隙水压力，从而导致土体强度降低，坡体的稳定性随之降低，因此预测的滑坡发育程度与降雨量呈正相关.

4.2 地震作用下的稳定性评价结果

地震是诱发浅层黄土滑坡的又一重要外因，根据已有数据得到地震情况下的稳定性评价结果（图7）. 地震加速度系数为0.05时失稳面积为0.39 km2，地震加速度系数为0.1时失稳面积为0.66 km2，地震加速度系数为0.2时失稳面积为2.26 km2. 预测结果表明失稳面积随地震加速度的增加而增加，烈度越大的地震越容易诱发滑坡，这与敏感性分析得出的结果相同. Scoops3D模型通过预定水平地震加速度的方式考虑地震对斜坡的影响，相当于增加滑动体所受切应力，使坡体的易滑性增加.实际情况中地震对坡体的影响不止是切应力的增加，震动对黄土自身强度也有较大影响，所以预测得出的结果比实际更保守.

4.3 降雨地震耦合作用下稳定性评价结果

结合降雨条件和地震条件，分别对中雨条件和暴雨条件的研究区增加3个级别的地震加速度，评价降雨地震耦合作用下的斜坡稳定性，结果如图8所示. 对比图6～8，预测结果显示，双因素失稳区面积远大于单因素失稳区面积. 对比图8（a）～（c）和（d）～（f），发现暴雨触发失稳面积远大于中雨触发失稳面积，暴雨和地震耦合的情况下触发的滑坡分布范围更广. 暴雨条件下，随着地震加速度的增加不稳定区的面积增加幅度更大，说明在暴雨的影响下坡体对地震加速度的响应更敏感.这与其他学者的研究成果相符合，即受雨水入渗影响的土体在地震动荷载作用下，由于孔隙崩塌和颗粒重排导致骨架重构而产生残余变形，孔隙体积的压缩使得孔隙水压力上升，有效应力降低，土体结构强度进一步下降并在动荷载的持续作用下产生液化破坏[13]. 预测结果显示地震和降雨的持续影响效应会对黄土斜坡稳定性产生耦合削弱作用，引发大量的浅层黄土滑坡.

图6 降雨作用下稳定性评价图. （a）无雨状态；（b）中雨状态；（c）暴雨状态Fig.6 Stability evaluation under rainfall: (a) no rain; (b) moderate rain; (c) heavy rain

图7 地震作用下稳定性评价图. （a）Keq=0.05；（b）Keq=0.10；（c）Keq=0.20Fig.7 Stability evaluation under earthquake: (a) Keq=0.05; (b) Keq=0.10; (c) Keq=0.20

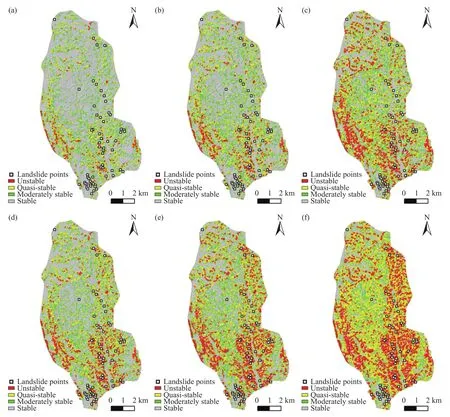
图8 降雨地震作用下稳定性评价图. （a）中雨+0.05；（b）中雨+0.10；（c）中雨+0.20；（d）暴雨+0.05；(e)暴雨+0.10；（f）暴雨+0.20Fig.8 Stability evaluation under rainfall and earthquake: (a) moderate rain +0.05; (b) moderate rain +0.10; (c) moderate rain+0.20; (d) heavy rain +0.05;(e) heavy rain +0.10; (f) heavy rain +0.20

4.4 预测结果分析

图9显示了降雨、地震、及其两者耦合条件下稳定等级的滑坡体积和面积大小分布. 图9（a）显示了滑坡体积大小分布情况，研究区滑坡体积大多分布在103～106m3，且降雨强度和地震加速度的增加会使滑坡体积分布更分散，即降雨和地震会诱发更多极大或极小型的滑坡. 滑坡体积的中位数随地震和降雨条件的增加呈增加状态，说明降雨和地震的增加会诱发更大规模的滑坡. 图9（b）显示了滑坡面积大小的分布情况，研究区在无雨情况下，地震的发生只能触发少量的滑坡；但当降雨发生时，地震的发生会触发大量滑坡发生. 两种条件中雨水的入渗是诱发滑坡的主要原因，在此条件下土体的抗剪强度降低、且自重增加，耦合地震条件会触发部分濒临失稳的坡体，引发更多的滑坡.

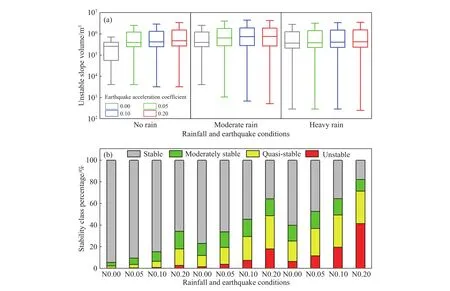
图9 失稳斜坡体积统计图（a）和稳定性分级面积堆积图（b）（图中N指无雨，M指中雨，H指大雨，如M0.05指中雨和0.05地震加速度系数耦合情况）Fig.9 Volume statistics of unstable slopes (a) and stacking diagrams of the graded area of stability (b) (N refers to no rain, M refers to moderate rain, and H refers to heavy rain. For example, M0.05 refers to the coupling of moderate rain and 0.05 earthquake acceleration coefficient)

为了进一步分析降雨和地震对滑坡的影响并验证预测结果的可靠性，本文根据对比预测失稳区与实际失稳区，用混淆矩阵法和ROC曲线法对评价结果进行精度检验. 通过预测精度来评价降雨或地震对黄土斜坡稳定性的影响，并确定研究区浅层滑坡的实际触发条件.

混淆矩阵法通过对比模拟结果和真实发生结果，将结果分为真正（预测失稳且实际失稳）、真负（预测稳定且实际稳定）、假正（预测失稳但实际稳定）、假负（预测稳定但实际失稳）4类，计算得到真正率（真正与真正和假负的和的比值）和假正率（假正与假正和真负的和的比值）和精度（真正和真负的和与总样本数的比值）来评价模型适用性.一般认为真正率/假正率大于1的模拟符合标准，真正率越大、假正率越小、精度越高的模拟结果更精准[32]. 结果表明暴雨情况下的预测结果与实际滑坡点分布最为接近，暴雨且不发生地震的情况下模拟结果最好，真正率为0.67，假正率为0.20，精度为0.74，真正率/假正率为3.35，符合预测精度指标（图10）. 这说明TRIGRS和Scoops3D组合模式能较准确预测流域尺度的浅层黄土滑坡.

对2种地震情况的指标分析表明，真正率与地震加速度呈正相关，原因是地震加速度的增加导致预测结果中失稳点的数目增加，实际情况中微地貌、人类活动等模拟中没有考虑的因素已经触发部分地震滑坡，导致真正类的点数增加. 同时，假正率与地震加速度也呈正相关，当地震加速度系数为0.2时假正率高达0.46，高地震加速度条件下得到的失稳区在实际环境下难以触发，导致假正类的点数增加. 此外，预测精度与地震加速度呈负相关，原因是地震加速度小的条件与实际条件更为接近. 这表明与实际条件更接近的预测条件能得出更高精度的预测结果. 对3种降雨情况的指标分析表明，在无雨条件下结果呈现出低真正率的特点，原因是无雨条件只能预测最容易失稳的滑坡，而实际大多数滑坡是在降雨、地震、河流冲刷、地下水活动及人工活动等复杂因素的影响下触发，这部分滑坡没有被无雨状态下的模拟预测到. 暴雨条件比无雨和中雨条件真正率大，原因是实际的滑坡更多是由比中雨更大的雨触发，暴雨条件下的结果包含更全面的降雨滑坡.

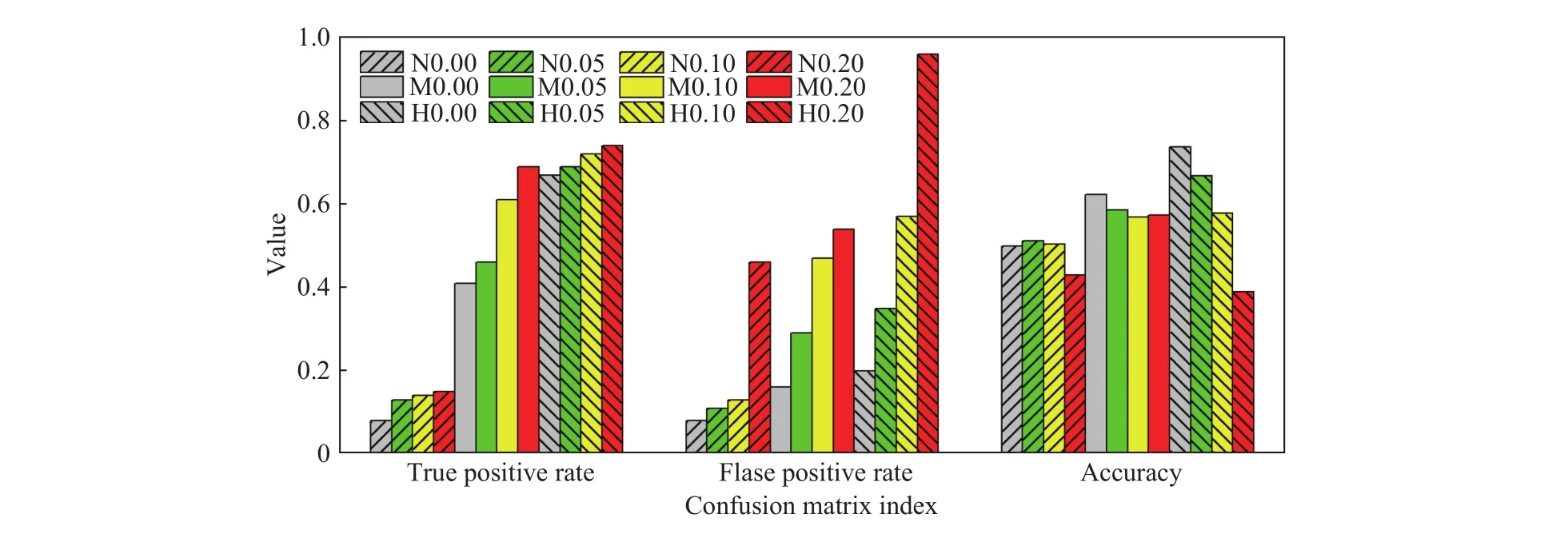
图10 混淆矩阵结果Fig.10 Confusion matrix result

3种降雨情况中（N0.00，M0.00和 H0.00），暴雨条件下的精度是最高的，说明暴雨条件预测结果与实际情况更吻合，实际触发的滑坡多数是由更大降雨触发，这也与其他研究相吻合[36].

ROC曲线法可以反应预测结果与实际结果的拟合情况，广泛应用于各种领域[37]. 对于滑坡预测，利用Arcgis软件统计预测结果中的不同稳定性等级，并计算不同稳定性等级区中实际滑坡点的数量，以稳定性等级占比为横轴，滑坡点占比为纵轴，绘制ROC，通过计算曲线下面积AUC来评价模拟结果，AUC越大说明预测结果越准确. 对于本文研究的问题，AUC越大说明预测结果与实际结果拟合度更好，与实际触发滑坡的条件越接近.

对比3种降雨条件下的ROC，图11（a），发现降雨强度越大的预测结果与实际情况更匹配，这也与混淆矩阵法得到的结果相同，说明已有滑坡点大部分由高于中雨条件的降雨触发. 暴雨条件下的预测结果AUC为0.73，也证明此次研究结果是比较可靠的.

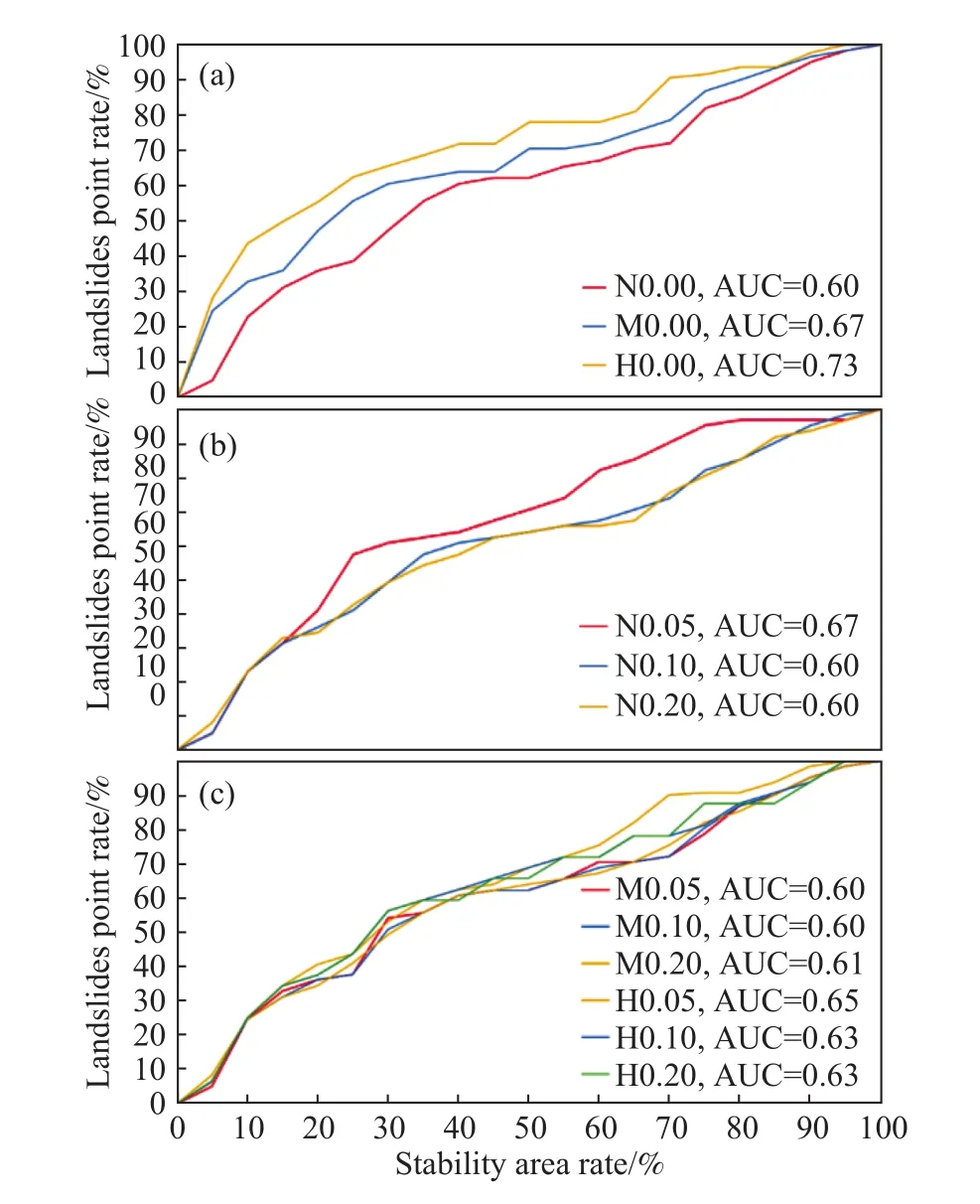
图11 ROC 曲线评价结果. （a）降雨情况；（b）地震情况；（c）耦合情况(图中N指无雨，M指中雨，H指大雨. 如M0.05指中雨和0.05地震加速度系数耦合情况）Fig.11 ROC curve evaluation results: (a) rainfall; (b) earthquake; (c)coupling (N refers to no rain, M refers to moderate rain, and H refers to heavy rain, M0.05 refers to the coupling of moderate rain and 0.05 earthquake acceleration coefficient)

对比3种地震条件下的ROC，图11（b），地震加速度系数为0.05时得出的结果与实际情况拟合程度最高，推测此类亚稳定滑坡已经被其他因素触发. 地震加速度大时AUC较小，原因是高地震加速度触发的滑坡在实际情况中触发条件严苛，其他因素不容易触发此类滑坡，这与混淆矩阵法得到的结论相同. 较小的地震加速度条件更符合实际条件，得到的预测结果也就更符合实际结果.

对比耦合条件，图11（c），下的ROC的AUC都较低，说明耦合条件产生的滑坡点与实际滑坡点差别较大，前文混淆矩阵结果也显示耦合条件下假正率较高，大量假正类的点导致AUC偏小，这类滑坡点在极端特殊条件下是不稳定的，需要加强对此类滑坡的监测预警.

5 结论

（1）组合TRIGRS渗流模型和Scoops3D确定性模型评价降雨或地震条件下的浅层滑坡稳定性，其优点在于可以考虑到黄土的非饱和特性与水分的差异性分布，进而模拟不同降雨和地震条件下触发滑坡的场景.

（2）混淆矩阵法和ROC曲线联合验证表明，TRIGRS和Scoops3D的组合方法可用于预测浅层黄土滑坡稳定性，且暴雨条件下的结果评价精度最符合要求. 这说明该组合方法能作为预防降雨或地震诱发滑坡的工具，对黄土地区的防灾减灾具有重要参考价值.

（3）降雨事件中，随着土壤含水量的增加，土自重的增加，土体抗剪强度也随之降低，导致斜坡驱动力增加. 对于该研究区，大部分已经触发的滑坡是由强降雨条件触发. 地震作用在坡体上也会使坡体稳定性降低，预测结果表明两者耦合的情况下会出现大面积黄土滑坡失稳现象，比起单一触因产生更多的浅层黄土滑坡.