循环水养殖池内鱼类运动数值模型的建立——以许氏平鲉为例

刘海波，任效忠*，张倩，毕春伟

(1.设施渔业教育部重点实验室(大连海洋大学 )，辽宁 大连 116023；2.大连理工大学 海岸和近海工程国家重点实验室，辽宁 大连 116024)

工厂化循环水养殖系统(recirculating aquaculture system，RAS)具有占地面积少、资源高效利用、不受自然环境影响和制约等特点，被认为是21世纪水产养殖业发展的主导方向之一。养殖池作为工厂化养殖系统主要的生产单元，是鱼类赖以生存的场所，其流态和水质能够直接影响鱼类的生长质量[1]，甚至鱼类在特定的水动力环境下可以达到最佳的生长效果[2]。而水动力条件不良对固体废弃物管理、水质，以及鱼类的生理和行为均会造成影响，进而影响生产潜力和经营效益，因此，养殖池的水动力性能是养殖池设计的重要关注点。目前，有关循环水养殖池系统流场研究中以假设不考虑养殖生物的影响建立简化的纯流场研究模型为主流，循环水养殖主要特点之一是高密度养殖，简化的研究与循环水养殖实际仍有一定差距。探索不同鱼类对水动力条件的差异需求，已成为工程水动力学与循环水养殖交叉结合研究的必然发展方向。研究鱼类与系统水动力特性间的相互影响，不仅可以为鱼类的福利化养殖、系统设计优化及养殖标准建立奠定前期理论基础，而且可为养殖生产提供理论和技术支持。

近些年，养殖鱼类与水动力特性之间的相互影响被越来越多的学者所关注，而鱼的存在对养殖池流体特性的影响已得到证实[3]。Masaló等[4]通过声学多普勒测速法(ADV)的监测量化研究，以斑马鱼为对象，分析了鱼密度与鱼游泳活动产生的湍流之间的关系，结果表明，由鱼类游泳活动引起的湍流与养殖密度呈正相关关系。Plew等[5]分别在有大西洋鲑和无大西洋鲑的养殖池内使用声学多普勒测速仪测量养殖池内流速，发现有鱼养殖池的湍流动能、湍流强度和湍流耗散率高于无鱼的情况，鱼的存在改变了养殖池水体的平均速度、湍流和氧气的分布，并增加了溶解氧的湍流输送。Masaló等[6]通过研究鱼类对圆形水池平均流速和流速剖面的影响，发现由于鱼类游动引起的紊流增加了运动涡流黏度，进而导致靠近出口的养殖池中心速度显著降低。

随着计算机技术和计算机流体力学(CFD)技术的逐渐成熟，CFD具有计算快捷、成本较低、同一数值模型可开展大量工况研究、获取流场信息丰富等优点，被广泛应用于工程水动力研究中，也成为循环水系统流场研究的主要技术手段之一。Labatut等[7-8]采用CFD技术对养殖池流场特性开展了数值模拟研究，结果与试验数据具有良好的一致性。Ji等[9]设计了一种水下自主机器人，采用CFD分析方法，分析了机器鱼周围的流量和压力。为减少机器鱼功率消耗，冯亿坤等[10]将仿生鱼作为研究对象，基于CFD方法利用动网格技术建立了鱼体-流体耦合的三自由度(3-DoF)自主游动计算模型，对仿生金枪鱼模型从静止开始到稳定巡游的过程进行了模拟。

随着中国水产养殖业发展，养殖品种不断变化，许氏平鲉Sebastesschlegelii逐渐成为中国北方沿海地区新兴的养殖对象之一，因其肉质鲜美，受到越来越多的关注。因此，以许氏平鲉作为研究对象，探索鱼类运动对养殖池内的流场影响具有一定的生产价值。目前，国内外关于鱼类运动对养殖池内流场影响的研究相对较少，鱼类与流体相互影响的研究成果主要基于试验研究获得，鱼类仿生模型及其与流场的相互影响模型的构建仍是难以解决的科学问题之一。本研究中，通过建立二维、三维鱼类的仿生运动模型及鱼类-流体间的流固耦合数值模型，模拟鱼类与养殖池流场的相互影响，以期为循环水养殖系统水动力的设定提供参考依据。

1 仿生鱼运动方法

Breder[11]将鱼类游动模式划分为摆动尾鳍模式(ostraciiform)、鳗鲡模式(anguilliform)和鲹科模式(caragiform)。Barrett等[12]提出鱼体运动可以通过二次曲线和正弦曲线合成得到，鱼体的运动可以近似看作从鱼头部向尾鳍传递波幅逐渐增大的正弦曲线。本文中采用CFD方法对鱼类摆尾运动进行数值模拟，采用的鲹科运动方程[13]为

y(x,t)=a(x)sin(kx-ωt),

(1)

a(x)=a0+a1x+a2x2。

(2)

其中：x为体长方向的坐标；y(x,t)为t时刻x处的纵向位移(m)；a(x)为鱼体横向波幅包络(m)；k1为波数(m-1)，k1=2π/λ，λ为体波波长(m)；ω=2πf，f为尾鳍摆动频率(Hz)。本文中各常数取值[14]：a0=0.02，a1=-0.008，a2=0.16，λ=0.95 m，f=1 Hz。

使用MATLAB软件将各参数带入鱼体运动方程，并取4个不同时刻仿生鱼中心线位置(图1)。

图1 仿生鱼体波曲线Fig.1 Bionic fish body wave curve

为实现仿生鱼运动，首先要指定运动区域，定义仿生鱼的运动类型。Fluent可以通过编写自定义的UDF宏文件定义指定区域的运动类型。由于柔性鱼体的波动既包含了节点运动也包含了区域变形，故本文采用UDF宏中DEFINE _GRID_MOTION来控制每一个节点的运动。对于尾鳍的运动，考虑其做周期性的波动，故基于鲹科运动方程来拟合尾部的摆动。运动方程为

y=(0.02-0.008x+0.16x2)×

sin(k1x-ωt)。

(3)

其中：x为点坐标；t为时间；y为x点处t时刻的增量(m)。尾鳍在y轴方向的位移与x的坐标相关，k1t通过生成不同的波数构造相位差，ωt使得相位随着时间变化，从而造成鱼体波的传播，实现鱼体尾鳍波动。在编写仿生鱼三维运动方程时，在二维的基础上转换坐标，将y轴方向上的运动转换为z轴方向的运动。同时输入头部坐标及三维鱼体长度，确定鱼体波动的起点坐标及波动距离，最后对UDF宏进行编译和加载。

2 鱼类-流体流固耦合数值模型建立

2.1 湍流模型

RNG k-ε模型在标准k-ε模型的基础上提供了考虑低雷诺数流动黏性的解析公式，提高了湍流漩涡的模拟精度，这一优点使得RNG k-ε模型在模拟养殖池的流态时有更高的可信度和准确度。本文的仿真计算中，循环水在养殖池流态中易引起湍流和漩涡，加入鱼类尾鳍的摆动则更易形成漩涡。由于仿生鱼尺度较小，属于低雷诺数范围，因此，采用RNG k-ε模型能更准确地模拟养殖池内流态特性。

RNG k-ε模型的表达形式为

Gk-ρε，

(4)

(5)

μeff=μ+μt，μt=Cμρε2/k。

其中：μt为湍流黏度(Pa·s)；μ为运动黏度(Pa·s)；ε为湍流耗散率(m2/s3)；k为湍流动能(m2/s2)；ρ为流体密度(kg/m3)；Gk为由层流速度梯度产生的湍动能项(kg/(m·s3))；Cμ、C1ε、C2ε为经验系数。计算时各经验常数[15]：Cμ=0.084 5，αk=αε=1.39，C1ε=1.42，C2ε=1.68。

2.2 二维运动模型

2.2.1 二维仿生鱼模型选择 选择最常见的NACA-0012翼型剖面用于二维鱼体模型的仿真。仿真运动模型建立过程如下：首先使用Profili软件将翼型数据点导入Excel表格中，然后用CAD软件中的SPLINE命令粘贴各数据点坐标并将各点闭合，生成如图2所示封闭曲线，生成面域并导出ACIS文件，最后将ACIS文件导入ANSYS Design Modeler中(图3)。

图2 CAD中二维鱼体模型Fig.2 2D fish body model in CAD

图3 ANSYS中生成的流体域Fig.3 Fluid domain generated by ANSYS

鱼的二维运动区域设为一矩形区域，左侧设为速度进口(velocity-inlet)用来定义流场运动方向，进水流速v=0.1 m/s，右侧设置为压力出口(pressure-outlet)，上、下壁面命名为wall。二维鱼体长(l)=0.1 m，在0.2 m×0.3 m的区域内运动(图4)。

图4 计算域示意图Fig.4 Schematic diagram of calculation domain

2.2.2 网格划分及模型计算参数设定 使用ICEM-CFD软件划分计算区域网格，为提高数值模拟的精确性，采用三角形网格对二维平面内鱼体轮廓周围进行网格加密处理，通过添加膨胀层(inflation)处理因尾部运动产生应力高度集中的区域，膨胀层网格通过延边界的法向拉伸提高网格精度，可由三角形和四边形网格组合形成(图5)。选用正交质量(orthogonal quality)对网格进行质量评定。网格的节点数为3 816，网格数为7 198。网格的平均正交质量为0.980 36，最大正交质量为1，网格质量满足要求。

图5 流体域网格划分Fig.5 Fluid domain meshing

采用瞬态(transient)模型模拟鱼类运动随时间的变化过程，流体材料设定为液态水(water-liquid)，压力速度耦合方式选择SIMPLE算法。压力、动量基于二阶迎风离散格式(second order upwind)求解，其余选项按默认设置。

2.3 三维运动模型

2.3.1 三维仿生鱼模型的选择 以许氏平鲉作为仿生对象建立三维仿真运动模型，许氏平鲉属于暖温性底层鱼类，在循环水养殖系统中除觅食外大部分时间处于静止状态，因此，本文中的运动模型设置为仿生许氏平鲉在循环水养殖系统中克服水流做原地摆尾运动。

本文中基于Solidworks建立三维鱼体模型，主要研究尾鳍摆动对养殖池内流场的影响，考虑到实际鱼体外形复杂，在动网格计算中边界运动幅度较大，因此，在建模过程时对除尾鳍外的所有部分做了简化处理。首先，选择在前视基准面中生成实体草图，绘制一条中心线并通过智能尺寸命令确定鱼的体长，然后用草图工具添加许氏平鲉原型图片(图6)。使用样条曲线绘制许氏平鲉轮廓，通过放样曲面生成三维鱼型实体，模型呈现出在自然状态下直线型的仿生鱼(图7)。然后将鱼体模型保存为IGES文件，导入ANSYS中进行后续建模。

图6 许氏平鲉Fig.6 Schlegel’s black rockfish Sebastes schlegelii

图7 Solidworks中仿生鱼三维模型Fig.7 3D model of bionic fish in Solidworks

2.3.2 养殖池模型的选择 在构建三维鱼类-养殖池模型时，以任效忠等[16-17]建立的方形圆弧角养殖池模型为基础，建立单向流-固耦合(unidirectional fluid-solid coupling)数值计算模型。方形圆弧角养殖池是养殖中应用较多且流态较好的养殖池型[18]，在方形圆弧角养殖池中嵌入许氏平鲉仿生鱼体，鱼体长l=10 cm，最大宽度b=0.85 cm，最大高度h=2.7 cm。仿生鱼做摆尾运动，鱼体前2/3轻微摆动，后1/3做正弦摆动，摆动频率f=1 Hz，周期T=1 s。尾鳍在尾柄的带动下做大幅度摇摆运动。本文中构建模型重点关注仿生鱼尾鳍摆动对流场的影响，不考虑浮力、重力等因素，选择水作为代替鱼体的材料，保证仿生鱼在水中摆动过程中保持位置不变。

养殖池模型采用方形圆弧角养殖池，长(L)×宽(B)=1 m×1 m(长宽比L/B=1∶1)，圆弧角半径R=0.25 m(相对弧宽比R/B=0.25)，水深H=0.2 m(径深比B/H=5∶1)。两个进水管分别布设于养殖池相对的直边壁中间位置，进水管垂向均匀开9孔，进水孔中心距池壁距离C=0.01 m(进径比C/B=0.01)。对养殖池其他结构参数进行简化处理，假设养殖池高等于水深，进水管与养殖池同高，射流速度v=1 m/s，流量Q=0.470 m3/h，如图8(a)所示。导入鱼体后系统模型如图8(b)所示，初始条件下鱼体位于距池壁0.25 m处，鱼体中心距池底0.1 m，头部方向与x轴方向相反，尾鳍相对于鱼体位于y轴的正方向，鱼体初始情况下处于直线状态。

图8 方形圆弧角养殖池模型Fig.8 A model of fish square arc angle aquaculture tank

2.3.3 网格的划分与计算 在划分三维鱼类-养殖池模型网格时，整体采用四面体网格，同时选择局部加密的方式对进水口、出水口及鱼体表面特别是鱼尾鳍处进行网格加密处理(图9)，鱼体内部不划分网格。对于远离鱼体和进出水口的流体区域，计算时不做网格加密处理(图10)。网格的节点数为267 973，网格数为1 489 817。网格的平均正交质量为0.863，最大正交质量为0.997，网格质量符合要求。

图9 鱼体表面网格划分示意图Fig.9 Diagram of mesh division on fish surface

图10 三维鱼类-养殖池网格划分结果Fig.10 Results of mesh division of 3D fish-aquaculture tank

动网格技术可以用于模拟流体域边界随时间改变的问题，本文采用动网格来实现鱼体的运动。常用的有3种网格更新方法，分别为光顺方法(smoothing)、动态层方法(layering)及网格重构方法(remeshing)。其中扩散光顺作为光顺的一种方法，适用于任何网格类型，而尾鳍的运动和变形主要是通过定义网格节点位置的变化来实现的，但尾鳍摆动具有大幅变形的特点，运动边界位移较大。因此，本文中选择扩散光顺和网格重构相结合的方法，在计算过程中将尺寸变化过于剧烈或畸变率过大的网格集中在一起进行局部网格重新划分，以保证网格运动后的质量。

2.3.4 模型计算参数设定 本文中计算模型假设为养殖池内水体为不可压缩黏性流体；只考虑鱼类运动对养殖池流场影响，无其他生物及颗粒等；养殖池内温度恒定，鱼类运动不影响池内水体温度；假设重力与浮力作用相抵，且鱼体不发生z轴方向位移。

本文中建立的模型重点关注鱼类运动对养殖池内流场的影响，鱼类位置随时间变化进而鱼体周围流态也发生相应变化，因此，选择瞬态(transient)求解方式。为建立仿生鱼运动对养殖池内流态的影响，建立单向流-固耦合计算模型，流体材料设置为液态水(water-liquid)。使用动网格技术中的扩散光顺和网格重构法实现尾鳍摆动，其中扩散系数(diffusion parameter)设置为1.5。连续相和离散相均采用压力隐式求解方法，选用SIMPLE算法对压力和速度进行耦合，压力、动量基于二阶迎风离散格式求解，湍流动能、湍流耗散率基于一阶迎风离散格式(first order upwind)求解。设定压力的亚松弛因子(under-relaxation factors)为0.3，动量的亚松弛因子为0.7，湍动能和湍流耗散率的亚松弛因子为0.8，其他项保持默认设置。计算系统模型具体初始边界条件设置如表1所示。

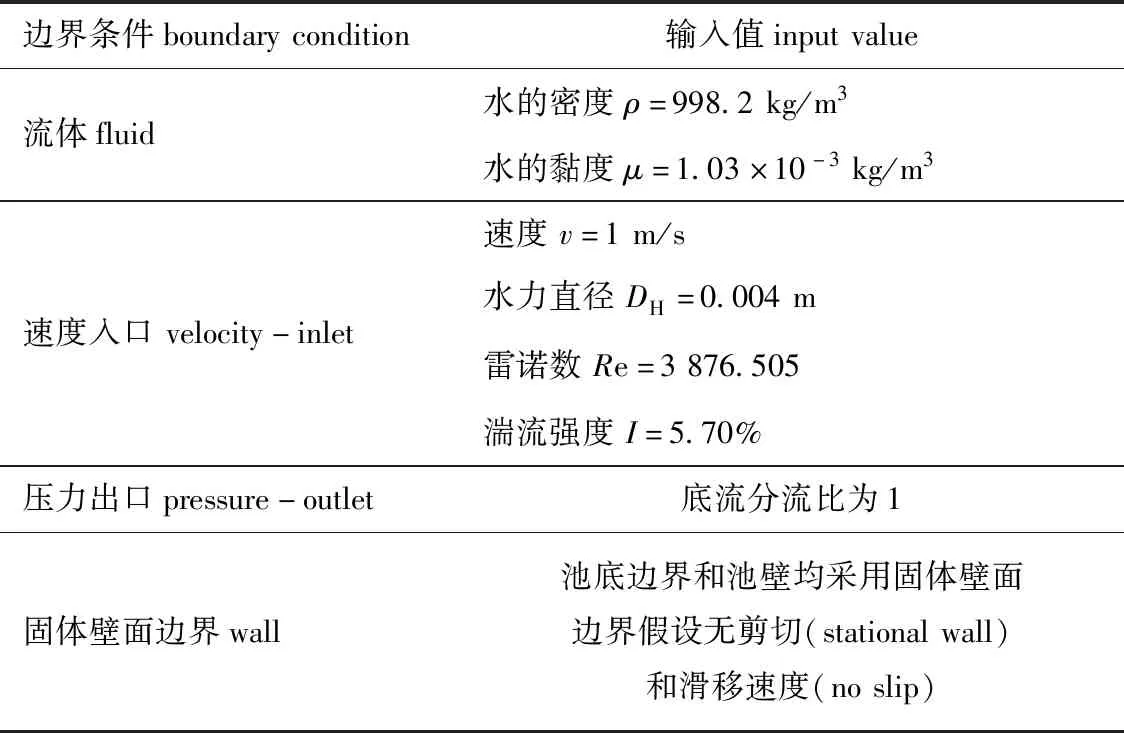
表1 数值计算初始边界条件Tab.1 Initial boundary conditions for numerical calculation

3 数值模型的仿真结果分析

3.1 二维平面仿生鱼运动模型

基于许氏平鲉仿生鱼运动的模型模拟计算了仿生鱼运动过程，监测了二维平面中仿生鱼运动对流场压力和速度的影响，提取仿生鱼一个摆尾周期内不同时刻的压力云图和速度云图(图11、图12)。

流体域内流场不仅受入口水流的影响，也受到鱼体运动的明显影响，通过动网格预览可以观察到，仿生鱼从静止状态开始做摆动运动，从鱼头位置到鱼尾位置波动幅度逐渐增大。从鱼头部位首先波动，鱼头位置波动幅度小因而对周围流场的影响也小，随着体波的传递波幅逐渐增大，鱼体对周围流场的影响也逐渐明显，尤以尾部波动幅度最大，其对流场的影响也相应更明显。

图11和图12显示了鱼一个摆尾周期内的流场压力和流场速度云图，在t=0时刻，鱼尾部由静止向y轴正方向摆动，摆动运动方向的鱼体压强总是高于另一侧，即摆动运动方向一侧由于摆动产生正的相对压强时，对称位置则会产生负的相对压强。由于仿生鱼尾部的摆动具有周期对称性，在T/4与3T/4，T/2与T时刻的压强场均呈相反关系。鱼在摆尾过程中尾部两侧周期性地交替出现高压区和低压区，是鱼体产生向前推力的主要来源。速度云图则能很好地体现流场内速度的变化情况。T/4与3T/4，T/2与T时刻的速度场不再具有对称性，在一个周期内高速度场始终出现在尾部摆动方向一侧，且随着摆尾次数的增加尾部周围的速度呈现出逐渐增加的趋势。鱼体周围速度监测现象直观地证明了鱼的存在改变了系统流场，这表明，鱼类是循环水系统流场构建中不可忽视的主体之一。

图11 二维仿生鱼周期T内的压力云图Fig.11 Contour maps of pressure with two-dimensional bionic fish in period T

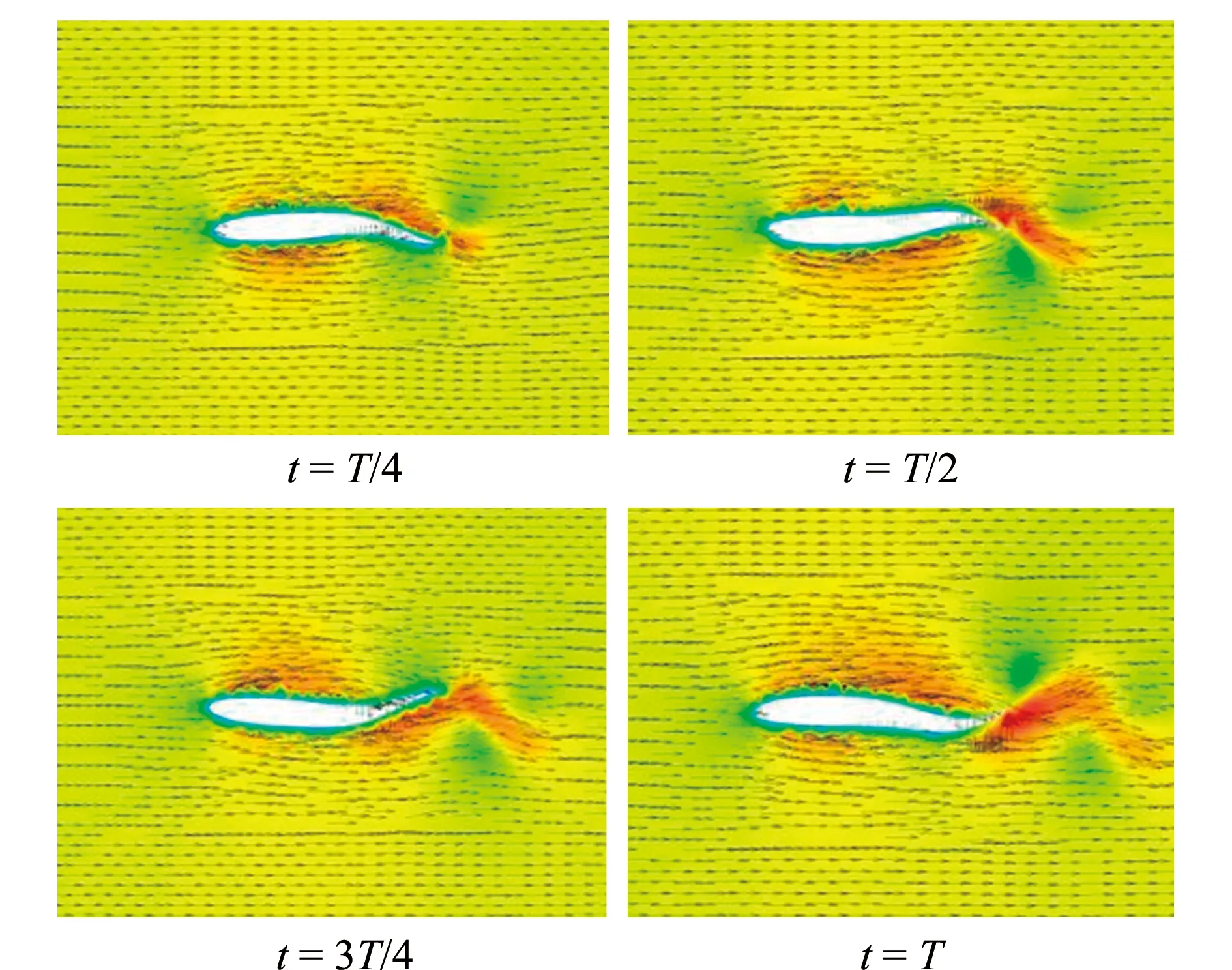
图12 二维仿生鱼周期T养殖池内流速分布特征图Fig.12 Contour maps of velocity with two-dimensional bionic fish in period T

由此可见，仿生鱼的波动对周围速度场和压力场均产生了不同程度地影响，这些影响在尾部最明显。随着仿生鱼尾部的摆动，一个周期内在鱼体后方逐渐形成一系列变化的压力场和速度场，压力和速度的影响在靠近尾部处最大，并随着逐渐远离尾部而逐步趋于消散。

3.2 三维空间仿生鱼运动模型

考虑到养殖池是一个三维的空间，鱼体的波动较为复杂。本文中以二维平面内尾鳍的波动为基础，x轴仍作为自变量，将尾鳍在y轴方向上的运动转换为z轴方向上的运动，而y轴则作为鱼体前进的方向。初始状态下养殖池中仿生鱼处于直线状态，t=0时刻，尾柄处向z轴负向摆动进而带动尾部的位移，在t=T/4时刻，尾部运动达到最大幅值，之后尾柄开始向z轴正向摆动，在t=3T/4时刻，尾部达到反向最大幅值(图13)。由此可见，鱼体由静止开始自主摆尾，由头部到尾部的摆动幅度逐渐增加，最终实现鱼体在相同周期下稳定波动。在整个运动过程中以仿生鱼的中心线为基准做周期性的正弦波动，从而带动整个鱼体的运动。

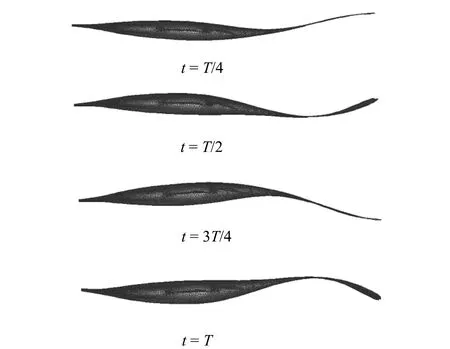
图13 三维仿生鱼运动俯视图Fig.13 Top view of 3D bionic fish motion

为监测三维仿生鱼尾鳍运动对养殖池流场的影响，以仿生鱼摆尾周期为时间单位，分别提取t=2T、4T、6T、8T时刻的系统无鱼工况和有鱼工况的速度分布云图(图14、图15)。尾鳍的摆动使尾部周围形成高流速区，随着时间的延长摆动对周围流场的影响逐渐明显且影响范围扩大。

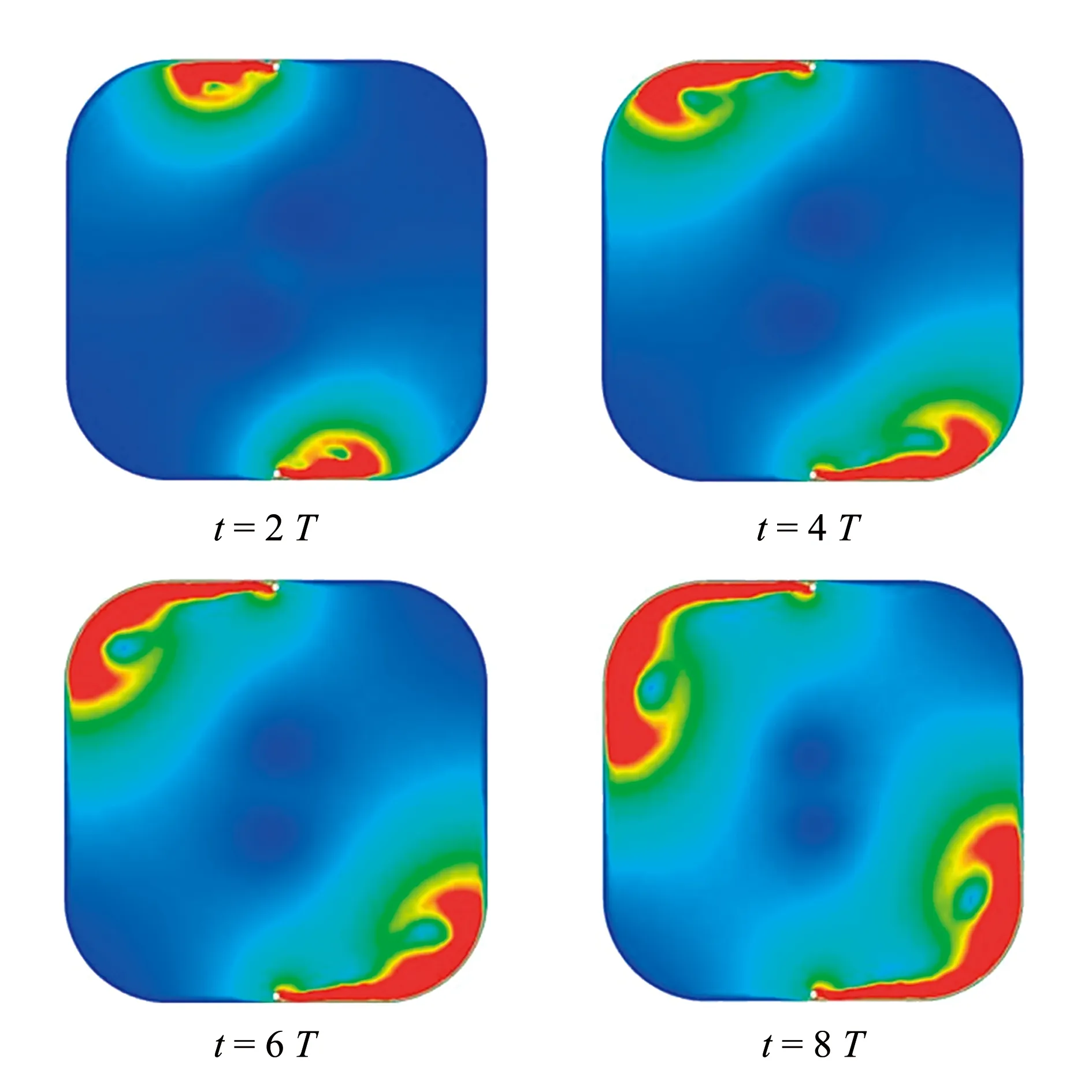
图14 无鱼工况池内横截面速度云图Fig.14 Contour maps of cross section in the tank without fish condition

图15 有鱼工况池内横截面速度分布云图Fig.15 Contour maps of cross section in the tank with fish condition

尾鳍摆动使周围流场产生一系列的脱落涡，一个周期内仅形成一个脱落涡(图16)。鱼尾摆动时形成的涡旋与养殖池中其他区域的水体相互碰撞造成能量消耗，进而影响养殖池内流速、紊动能等水力因子。尾鳍形成的涡旋与夏全新等[19]通过数值理论计算发现的“之”字形涡环链相吻合，进一步验证了运动模型的合理性。

图16 t=T/2时刻仿生鱼周围的三维涡量图Fig.16 Three-dimensional vorticity diagram around the bionic fish at t=T/2

4 结论

1)使用CAD、Solidworks等软件建立的仿生鱼模型可直接通过软件接口与ANSYS实现数值模型的共享和交换。

2)基于鲹科运动方程编写的UDF宏文件可用于定义二维平面及三维空间内仿生鱼的尾鳍运动，由于运动方程具有普适性，因此，基于相应的鱼体模型可以定义任一种类的仿生鱼运动。

3)二维平面内鱼尾的摆动会使周围流场产生压强差和速度差，而三维养殖池内尾鳍的摆动会在尾部末端形成一系列的环形脱落涡，与周围水体产生碰撞形成能量消耗，进而对养殖池内流场产生影响。