基于板厚补偿的921A钢与Q345钢靶板在截卵形弹体侵彻下的等效方法

王逸南，张建伟，王治，姚熊亮，杨娜娜

(1.哈尔滨工程大学 船舶工程学院，黑龙江 哈尔滨 150001；2.哈尔滨工程大学 机电工程学院，黑龙江 哈尔滨 150001)

0 引言

弹体侵彻是近年来不断升温的研究领域，基于其广泛的研究背景，深受国内外学者的关注，其中侵彻试验是舰船防护装甲和反舰武器研制阶段中不可缺少的研究手段。由于需要投入巨大的人力和物力资源，原尺度的侵彻试验十分稀少，主要是通过相似理论与方法对侵彻问题进行研究分析。相似理论是研究模型实验和原型实验相似性的理论方法，对于一些原型实验难于开展的侵彻问题，如何设计与原型相似的缩比模型成为关键问题，而相似理论正是回答这一问题的方法。

针对侵彻问题，目前相似理论的研究主要针对缩比相似规律以及缩比相似中的尺度效应等。王树有等[1]基于相似理论，推导了混凝土侵彻实验相似准则，提出了用混凝土侵彻模型实验代替原型实验的方法，并建立验证了相似准则。Wen等[2]开展了钝头弹丸低速撞击圆板实验，实验中圆板产生大变形或穿孔，他们指出在其实验范围内几何缩比方法满足相似性。刘源等[3]针对弹体刚体过载相似性问题，研究了非等比例缩比侵彻/贯穿相似规律，提出了非等比例缩比侵彻实验设计方法。甘宏伟等[4]运用数值仿真方法，分析了均质靶板的厚度和加筋板架结构不同弹着点对弹头穿靶能力的影响，并基于剩余速度理论，运用数值模拟和统计概率分析的方法，建立了加筋板架结构与均质靶板之间的等效关系。Song等[5]针对不同材料和板厚的薄板垂直侵彻问题，基于实验数据和相似理论分析得出了弹体剩余速度的预报公式。Jones等[6]针对几类不同弹头的弹丸低速侵彻圆板和方板问题开展实验，并验证了几何相似缩比方法的正确性。

针对侵彻靶板的模型与原型采用不同材料的情况，目前还是缺少相似性理论研究与设计方法。此方面的研究是有意义的，在一些问题中，选择不同靶材的靶板，其相应的制作成本差异颇大。采用真实靶材进行实验取得的实验结果尽管是最真实和最可信的，但是实验费用太高。若能找到弹体侵彻不同靶材的靶板之间的等效关系，则可以利用成本较低靶板材料等效替代高成本靶材，在保证实验结果有效情况下，既可降低实验成本，又可增加实验效率。目前国内外已经开展了一定程度的对于材料等效相似性的理论研究。Baker等[7]首先在书中第8节对侵彻材料相似方法做了简要而意义重大的介绍。Mullin等[8]通过实验和数值计算主要研究了锌和铝两种材料靶板侵彻的速度缩比方法，但没有给出速度缩比设计理论公式。此后，Mullin等[9]分析了高速侵彻问题影响因素并建立了π项，其中关键π项为v2/n，v为弹丸冲击速度(m/s)，n为靶板材料融化热量(kJ/kg)，这个无量纲量代表着弹丸动能与靶板融化能量的比值，他们通过保证此π项相等，设计不同材料靶板的撞击速度，并通过实验验证了“速度缩比方法”的有效性。Alves等[10]找到比例模型中冲击弹体质量比βg作为考察π项，通过修改初始弹体质量来达到等效目的。Mazzariol等[11]则对比了不同学者总结的等效方式，如MLT等效法、Calladine等效法、VSG等效法后，找到了一种新的修改初始速度理论公式来考察不同材料的相似性问题。但仍然不够充分，并没有等效材料靶板的有效设计方法，相关研究亟待开展。

本文针对截卵形弹体正侵彻均质钢板问题，采用补偿模型理论，以剩余速度为相似目标建立不同材料钢板侵彻的相似设计方法。首先针对文献[15]中的实验结果验证数值计算方法的有效性，然后对于921A钢和Q345钢两种材料不同厚度靶板进行侵彻计算，基于剩余速度数值计算结果探讨侵彻过程项的选取，最后基于补偿模型方法建立不同材料钢板侵彻的相似设计方法，找到材料等效工程化设计公式。

1 靶板等效的研究方法

1.1 靶板等效原则

若反舰导弹侵彻原型材料靶板消耗能量与弹体侵彻模型材料靶板消耗的能量相等，则认为二者之间的等效关系成立[12]。即在一定初速度条件下，侵彻过程中弹体消耗的能量相等，可用穿靶后弹体的剩余速度相等原则来表述靶板之间的等效关系。

基于剩余速度对侵彻建立起等效原则后，仍需通过理论公式找到具体等效设计的方法和思路。由于侵彻问题涉及因素众多，难以全部描述清楚，因此需要找到合理的简化方式，突出其中的主要影响因素，从而给出相似性设计方法的工程化预报公式。为此，借助无量纲分析及补偿模型建立，开展研究工作。

1.2 靶板等效量纲分析及补偿模型

量纲分析法[13]是在研究现象相似性问题的过程中，对物理量的量纲进行考察时产生的，是解决近代工程技术问题的重要手段之一，相对于其他方法具有较高的适用性。对于垂直侵彻均质平板的问题，对影响弹体侵彻剩余速度结果的物理量进行量纲分析，可以写出剩余速度vr的函数表达式[5]为

vr=f(ρp,L,D,A,N,ρt,H,v0,Epy,Ety,

Yp,Yt,Ept,Ett,Yps,Yts,εpf,εtf,μp,μt)，

(1)

式中：ρp为弹体密度(kg/m3)；L为弹体有效长度(m)；D为弹体直径(m)；A为弹头截顶长度(m)；N为弹体形状因子；ρt为靶板密度(kg/m3)；H为靶板板厚(m)；v0为弹体初始速度(m/s)；Epy、Ety分别为弹体弹性模量和靶板弹性模量(Pa)；Yp、Yt分别为弹体屈服强度和靶板屈服强度(Pa)；Ept、Ett分别为弹体硬化模量和靶板硬化模量(Pa)；Yps、Yts分别为弹体极限强度和靶板极限强度(Pa)；εpf、εtf分别为弹体失效应变和靶板失效应变；μp、μt分别为弹体材料泊松比和靶板材料泊松比。

针对本文等效仿真情况进行分析，弹体材料强度远大于靶板强度，侵彻过程中变形损伤程度很小，且材料在不同工况中未发生变化，因此与弹体相关的物理量Epy、Ept、Yp、Yps、εpf、μp等因素影响可以不考虑。921A钢和Q345钢两种靶板靶材虽然不同，但均为低碳合金钢，因此，两种靶板弹性模量、密度和泊松比十分接近，ρt、Ety和μt影响可以忽略。由于两种靶板材料不同，Ett、εtf、Yts和Yt不同。在较高碰撞速度下，弹塑性体侵彻碰撞点附近区域靶板材料的破坏特性主要由材料密度和强度起主导作用，结构效应退居次要地位[14]。但除了靶板屈服强度Yt，Ett和εtf对材料等效的影响也不可以忽略。

选取弹体直径D、弹头截顶长度A和弹体速度v0作为基本物理量，对(1)式进行简化，得

vr=f(v0,D,A,H,Yt,Ett,εtf).

(2)

对(2)式进行无量纲分析，可以给出无量纲函数关系形式为

(3)

2 靶板等效数值仿真分析

2.1 计算模型

采用文献[15]中的截卵形弹体靶板模型进行数值仿真计算并验证本文数值仿真方法的正确性，弹体为截卵形弹体，由弹体壳体和填充物两部分组成，弹体长370 mm，直径105 mm，截顶直径为20 mm，弹头圆弧半径180 mm，质量约16 kg.截卵形弹体为变壁厚头壳，柱段壁厚取10～14 mm.靶板大小为1 400 mm×1 000 mm，厚度为15.2 mm，靶板材料为921A钢，弹体壳体材料为30CrMnSiNi2A.

弹体与靶板模型均采取Lagrange算法的solid 164单元，弹体头部网格尺寸为0.5 mm，尾部渐变为2 mm.靶板模型应用了逐步过渡方法改变网格在靶板上的分布，引入无量纲参数λ[16](弹靶接触位置附近的网格尺寸Δl与弹体直径D之比)来考察网格得适用性。吴子奇[16]经过计算发现当λ=0.05时，网格尺寸已经适用于侵彻问题的计算。本文中靠近弹丸侵彻的区域网格密度较大，尺寸为2.5 mm，λ仅为0.023，完全可以进行弹体与靶板的接触运算。远离弹丸侵彻的区域网格密度较小，尺寸为10 mm.厚度方向上网格尺寸为1.5 mm.中心加密区域为弹径的4倍，为了模拟实际的实验条件，对靶板的4个侧面施加了固定边界条件。弹体及靶板几何模型和有限元模型如图1所示。

图1 弹体几何模型及靶板有限元模型

计算过程中，弹体壳体和靶板均采用带Mises屈服准则且与应变率相关的双线性弹塑性模型，应变率用Cowper-Symonds模型来考虑，填充物材料为线弹性模型，弹体和靶板的具体材料参数[16]如表1所示。

表1 弹体和靶板材料模型参数

在描述船用钢的高应变率强化效应时，Cowper-Symonds模型具有很好的有效性。其动态屈服应力与应变率的关系为

(4)

观察(4)式可以发现，考虑应变率的动态屈服强度峰值与屈服强度、硬化模量和失效应变相关，即

σy∝Yt+βEpεtf，

(5)

因此，(3)式中π项可以进行相应简化：

(6)

(6)式改写为π项的形式为

π=f(π1,π2,π3,π4)，

(7)

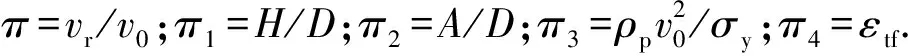
根据相似第二定理(π定理)，如果模型与原型相似，则需满足独立的π项相等，即

(8)

(9)

(10)

(11)

式中：上标p和m分别表示原型和模型。

对于本文研究的原型与模型材料不一致的情况，原型与模型π3、π4不相等，模型产生畸变，导致πp≠πm，物理过程不相似。因此需要采用补偿模型理论，设定π项之间是乘积关系[13]，建立原型与模型之间的相似关系，即

(12)

(13)

(14)

(14)式为不同材料等效关系的一般形式，本文中着重研究921A和Q345两种钢材之间的等效，失效应变均取为常数，因此(14)式右边第2项为一定值，可以进行如下简化处理：

(15)

式中：c1为应力项的幂次项系数。

(15)式代入(14)式中，得到

(16)

式中：x为等效系数。

由(16)式可以看出，只需根据数值仿真方法得到的已知等效板厚确定等效系数x，即可确定两种靶材靶板之间的等效关系。

2.2 数值仿真结果正确性验证

弹体侵彻靶板过程中会产生整体和局部的变形与破坏。平头弹丸对均质金属薄板的侵彻会产生碟型变形的拉伸与剪切混合失效模式[18]。截卵形弹丸对均质金属薄板的侵彻主要呈现为扩孔过程，最终产生花瓣型失效模式[19]。弹体正穿甲均质靶板毁伤过程如图2所示：弹体首先挤凿靶板，在靶板出现与弹体截顶面积大小相当的隆起(见图2(a))，继而形成塞块从靶板上脱离(见图2(b))；随后进入扩孔阶段，破口不断增大，靶板花瓣型失效模式逐渐形成(见图2(c))；最后随着弹体的飞出，破口形状趋于稳定。数值仿真得到的侵彻破口形状与文献[15]实验结果对比情况如图3所示。

图2 毁伤过程图

图3 数值仿真结果与文献[15]实验破口形状图

由图3可以看出：均质靶板垂直侵彻的仿真结果与实验结果接近，均出现花瓣型的失效模式；侵彻产生的破口基本呈现圆形，文献[15]中指出破口与弹体直径基本相同，破口直径约为115 mm.数值模拟结果中破口尺寸为113.3 mm，与实验结果十分接近。为了进一步验证数值仿真结果的正确性，对文献[15]中其他垂直加筋靶板的实验工况进行仿真计算，其中：大筋高度为68 mm，宽度为15.2 mm，两筋之间间距为600 mm；小筋高度为26 mm，宽度为7 mm；两筋之间间距为125 mm.与文献[15]实验结果进行对比，工况设置及计算结果分别如表2和图4所示。

本文建立的数值仿真模型计算得到的弹体穿靶后的剩余速度与文献[15]中的实验测定值比较接近，如表2中所示剩余速度相对误差控制在0.24%～0.73%之间。图4(a)中靶板破口直径为117.86 mm，图4(c)中靶板破口上下测量为117.9 mm，左右测量为112.2 mm.由于大筋强度较高，对底板支撑力度更大，因此图4(c)中破口左右长度较之上下长度略小一些。对比数值模拟毁伤图和实验结果，可以发现底板整体出现碟型隆起。弹体顶端挤压靶板，超过材料屈服强度后，截顶处四周产生星型裂纹，裂纹不断扩展最终形成花瓣型破口。

表2 数值仿真结果与文献[15]实验实测结果比较

图4 加筋板工况数值仿真结果与文献[15]实验破口形状图

加筋处毁伤破坏大致呈现两种：1)加强筋与底板连接处产生撕裂，撕裂后加强筋中的剩余能量使其继续弯曲变形达到图4中的毁伤效果；2)加强筋受弹体冲击直接产生剪切折断。数值模拟得到毁伤模式与实验结果相一致，验证了本文所建立的数值仿真模型的正确性。

2.3 靶板等效性数值仿真

首先，将舰船多采用的921A钢靶板的板厚分别选取为设计常用板厚8 mm、10 mm、12 mm、14 mm和16 mm.再通过选取Q345钢做为921A钢的等效材料，进行不同材料靶板侵彻作用下的等效规律研究。选择上文的截卵形弹体在初速度550 m/s下，垂直侵彻单层921A钢与8.5～19.5 mm板厚Q345钢靶板进行剩余速度的等效分析，两种靶材靶板剩余速度等效板厚拟合结果如图5所示。

图5 弹体侵彻921A钢与Q345钢后的剩余速度等效曲线

由图5可以得出，当弹体侵彻速度为550 m/s时，8 mm、10 mm、12 mm、14 mm和16 mm板厚的921A钢分别可以用8.9 mm、11.3 mm、13.5 mm、16.1 mm和18.9 mm板厚的Q345钢进行等效。为了排除数值等效的偶然性，通过将初速度设置为250～650 m/s考察得到的两种钢材靶板等效板厚，验证所得到等效板厚在不同速度下的等效性，各个速度下剩余速度计算结果如表3所示。

表3 垂直单层靶板剩余速度结果

从表3中可以看出：921A钢靶板与等效的Q345钢靶板在250～650 m/s初速度下，所得到的剩余速度相近；当弹体初速度为650 m/s时，针对12 mm厚921A钢靶板及13.5 mm厚Q345钢靶板的毁伤进行分析，当弹体初始接触到靶板时，不同钢材靶板的应变云图如图6所示。

通过图6(a)可以发现，由于在初试阶段中(1.5×10-2ms)921A钢靶板板厚比Q345更薄，应力波在其中传播时间更短，导致在其靶板背侧首先达到屈服应变极限从而发生失效。除此之外，两块靶板整体的应变趋势一致，随之观察两块靶板与弹体接触中心点的应力关系如图7所示。

图7 两种钢材侵彻中心点应力曲线

从图7中可以看出：921A钢靶板中应力更快达到峰值点后归于零点；基于不同的材料属性，921A钢的应力峰值会更高，但整体的应力变化曲线效果相同。靶板所受外力如图8所示，具体毁伤模式如图9所示。

图8 两种钢材靶板受力曲线

由图8可以看到：初始时刻弹体接触到靶板瞬时达到压力峰值；随着弹体的继续向前移动，会出现很短暂的坍塌和硬化循环，导致受力消失[20]；弹体随之逐渐稳定，靶板受力逐渐恢复，两块靶板所受外力形式一致。由图9可以看到：不同靶板均呈现出花瓣状破口形式，由于材料及板厚的区别，花瓣个数及形状会有微小的差异，但总体毁伤形式一致。因此，基于上述结论，判断所得到的13.5 mm厚Q345钢可以用来等效12 mm厚921A钢。

根据(14)式和(16)式，考察基于补偿模型的材料等效问题，主要是找到板厚H和动态屈服强度σy、失效应变εtf之间的关联。根据(4)式计算两种靶材的动态屈服应力，对于高强度船用钢侵彻问题属于材料高应变率问题，取应变率为1 000 s-1，计算得921A钢与Q345钢的动态屈服应力分别为1 004.3 MPa和655.5 MPa.采取上述等效板厚与计算结果，通过(14)式进行拟合可以得到方程如下：

(17)

本文着重针对921A钢与Q345钢进行分析验证，考察它们之间的材料等效板厚设计方法，因此可以将(17)式进行一定简化，将公式右侧第2项归入第1项中，如2.1节中所描述的针对(16)式中x参数进行拟合分析，得到两种钢材的等效性拟合曲线如图10所示，拟合后方程为

图10 921A钢与Q345钢等效性拟合曲线

(18)

921钢靶板8 mm、10 mm、12mm、14 mm和16 mm不同板厚代入(18)式，进行经验公式的可行性验证，与数值仿真计算结果进行对比，结果如表4所示。由表4可以看出，二者差异小于3.5%，验证了经验公式的正确性。

表4 数值仿真与经验公式计算等效板厚结果对比

2.1节中提到，补偿模型分析过程中如果原型和模型的弹头形式一致，那么将不会对等效结果产生影响。因此引入4种不同截径比的弹头，分别为尖卵形、10/105、30/105和40/105(其中前面数值代表截顶直径，后面数值代表弹体直径)，分别侵彻12 mm厚921A钢和13.5 mm厚Q345钢。他们的剩余速度如表5所示，毁伤云图如图11和图12所示。

表5 不同截径比弹头侵彻靶板剩余速度结果对比

图11 不同截径比弹体侵彻921A钢靶板的毁伤云图

图12 不同截径比弹体侵彻Q345钢靶板的毁伤云图

由表5中数据可以看到：两种材料靶板在对应板厚下受到侵彻冲击作用，剩余速度差别很小，满足等效条件。观察图11可以发现：随着截顶尺寸的增加，侵彻初始阶段的塞块也随之变大，而毁伤模式还是主体呈现出花瓣形破坏。对比图11和图12中两种不同厚度的921A和Q345靶板，发现毁伤模式几乎相同，只是撕裂过程中花瓣形状稍有不同，因此满足上文中有关侵彻问题无量纲π项的不同材料等效关系分析。

3 结论

本文针对截卵形弹体侵彻921A及Q345钢靶板的等效性问题展开研究。采取数值仿真的手段对侵彻问题进行模拟，并与文献[15]中的实验结果进行对比验证了其有效性。针对板材等效问题，建立起基于量纲分析的侵彻补偿模型，并与后续的数值仿真计算相结合。得出以下主要结论：

1)基于剩余速度相等原则及相应的受力和毁伤分析，得到了与多种板厚的921A钢靶板等效的Q345钢靶板厚度。8 mm、10 mm、12 mm、14 mm和16 mm板厚的921A钢靶板可以分别用8.9 mm、11.3 mm、13.5 mm、16.1 mm和18.9 mm板厚的Q345钢靶板进行等效替换。

2)基于量纲分析的侵彻补偿模型，引入数值计算结果获得拟合函数关系式，如(18)式所示。此公式表明921A钢板与Q345钢板的板厚之比等于材料动态屈服强度反比的0.330 78次方。

参考文献(References)

[1] 王树有，顾晓辉，赵有守.混凝土侵彻试验相似准则验证分析[J].南京理工大学学报，2005，29(5):43-46.

WANG S Y，GU X H，ZHAO Y S.Verification and analysis of similarity criteria for concrete penetration test[J].Journal of Nanjing University of Science and Technology，2005，29(5):43-46.(in Chinese)

[2] WEN H M，JONES N.Experimental investigation of the scaling laws for metal plates struck by large masses[J].International Journal of Impact Engineering，1993，13(3):485-505.

[3] 刘源，皮爱国，杨荷，等.非等比例缩比侵彻/贯穿相似规律研究[J].爆炸与冲击，2020，40(3):63-75.

LIU Y，PI A G，YANG H，et al.Study on similarity law of non-proportionally scaled penetration/perforation test[J].Explosion and Shock Waves，2020，40(3):63-75.(in Chinese)

[4] 甘宏伟，陈威，李吉峰，等.加筋板架结构与均质靶板等效关系的数值分析[J].四川兵工学报，2010，31(11): 20-22.

GAN H W，CHEN W，LI J F，et al.Numerical analysis of the equivalent relationship between the stiffened plate frame structure and the homogeneous target plate[J].Journal of Sichuan Or-dnance，2010，31(11):20-22.(in Chinese)

[5] SONG Q，DONG Y X，CUI M，et al.A similarity method for predicting the residual velocity and deceleration of projectiles during impact with dissimilar materials[J].Advances in Mechanical Engineering，2017，9(7):168781401770559.

[6] JONES N，BIRCH R S.On the scaling of low-velocity perforation of mild steel plates[J].Journal of Pressure Vessel Technology，2008，130(3):031207.

[7] BAKER W E，WESTINE P S，DODGE F T.Similarity methods in engineering dynamics:theory and practice of scale modeling[M].Newnes，North-Holland:Elsevier Science，1991.

[8] MULLIN S A，LITTLEFIELD D L，ANDERSON C E，et al.An examination of velocity scaling[J].International Journal of Impact Engineering，1995，17(4/5/6):571-581.

[9] MULLIN S A，ANDERSON C E，WILBECK J S.Dissimilar material velocity scaling for hypervelocity impact[J].International Journal of Impact Engineering，2003，29(1/2/3/4/5/6/7/8/9/10):469-485.

[10] ALVES M，OSHIRO R E.Scaling the impact of a mass on a structure[J].International Journal of Impact Engineering，2008，32(7):1158-1173.

[11] MAZZARIOL L M，ALVES M.Scaling the impact of a mass on a plate using models of different materials[C]∥Proceedings of the 4th International Conference on Impact Loading of Lightweight Structures.Cape Town，South Africa: Blast Impact and Survivability Research Unit，2014.

[12] 周岩，唐平，常敬臻，等.舰舷结构与均质靶板等效关系的基本方法[J].弹道学报，2008，20(1):30-34.

ZHOU Y，TANG P，CHANG J Z，et al.Basic method of equivalent relationship between ship side structure and homogeneous target plate[J].Journal of Ballistics，2008，20(1):30-34.(in Chinese)

[13] 徐挺.相似理论与模型试验[M].北京:中国农业机械出版社，1982.

XU T.Similarity theory and model test[M].Beijing:China Agricultural Machinery Press，1982.(in Chinese)

[14] 李建广，尹建平，任杰，等.超高速半穿甲战斗部侵彻多层间隔板缩比实验设计方法[J].兵器装备工程学报，2019，40(10):21-25.

LI J G，YIN J P，REN J, et al.Research on design method of scaling experiments for ultra-high-speed semi-armor-piercing warhead penetrating multi-layer spacer[J].Journal of Ordnance Equipment Engineering，2019，40(10):21-25.(in Chinese)

[15] 段卓平，张中国，李金柱，等.半穿甲战斗部对加筋靶板和均质靶板垂直侵彻的实验研究[J].弹箭与制导学报，2005，25(2):148-150，157.

DUAN Z P，ZHANG Z G，LI J Z，et al.Experimental research for warhead vertically penetrating homogeneous ribbings structural targets[J].Journal of Projectiles，Rockets，Rockets and Guidance，2005，25(2):148-150，157.(in Chinese)

[16] 吴子奇.弹目结合的反舰导弹对目标舰船靶标侵彻毁伤研究[D].哈尔滨:哈尔滨工程大学，2019.

WU Z Q.Research on the penetration and damage of anti-ship missiles on target ships[D].Harbin:Harbin Engineering University，2019.(in Chinese)

[17] 朱锡，张振胡，梅志远，等.舰船结构毁伤力学[M].北京：国防工业出版社，2013.

ZHU X，ZHANG Z H，MEI Z Y，et al.Damage mechanics of warship structure subjected to explosion[M].Beijing:National Defense Industry Press，2013.(in Chinese)

[18] 徐伟，侯海亮，朱锡，等.平头弹低速冲击下薄钢板的穿甲破坏机理研究[J].兵工学报，2018，39(5):883-892.

XU W，HOU H L，ZHU X，et al.Investigation on the damage mechanism of blunt projectile against thin plate[J].Acta Armamentarii，2018，39(5):883-892.(in Chinese)

[19] 宋卫东，宁建国，张中国，等.多层加筋靶板的侵彻模型与等效方法[J].弹道学报，2004，16(3):49-54.

SONG W D，NING J G，ZHANG Z G，et al.Penetration model and equivalence method of multi layered stiffened plates[J].Journal of Ballistics，2004，16(3):49-54.(in Chinese)

[20] VIJAVAN V，HEGDE S，GUPTA N K.Deformation and ballistic performance of conical aluminum projectiles impacting thin aluminum targets:influence of apex angle[J].International Journal of Impact Engineering，2017，110:39-46.