基于生成对抗网络的水声目标识别算法

薛灵芝，曾向阳，杨爽

(西北工业大学 航海学院，陕西 西安 710072)

0 引言

水声目标识别是水声探测领域的关键技术，近年来，随着人工智能的进一步发展，研究人员开始尝试将深度学习方法应用于水声目标识别。基于深度学习的目标识别方法可将传统的特征提取与分类识别相结合，实现特征自动提取与自适应学习，完成从输入信号到输出类别的一体化处理。

Park等[1]和Zhang等[2]利用卷积神经网络(CNN)对水声目标进行分类识别，其中CNN网络的输入样本为时频信号的图像信息，没有直接使用时频信息。江伟华等[3]针对非合作水声信道，提出一种基于人工神经网络的水声信号调制分类器，Zeng等[4]利用多任务贝叶斯稀疏学习算法提取水声目标特征，实现目标类型识别，实验过程采用多阵列任务学习，对于水声的采集方法要求太高。王强等[5]对于不同的深度学习网络，直接输入水声的时域信息，对比CNN与深度置信网络(DBN)对水声数据的分类识别能力，并分析CNN的滤波器结构与原始水声信号之间的关系。文献[6]提出基于CNN的水声小样本识别方法，利用不同的输入特征验证方法的识别性能，网络结构简单，对于不同的输入样本，需要进一步验证网络的泛化能力。Huang等[7]和Sheng等[8]针对水声目标噪声数据的特点，改进深度学习中的DBN，提升水声目标识别率，DBN可以利用概率模型学习原始数据的另外一种表征，尽可能保留原始数据中的概率分布特征，但在概率模型比较单一的样本下无法避免冗余特征带来的计算量增加。Xie等[9]提出基于玻尔兹曼机的水声目标识别方法，并利用实验数据对比，证实识别率由于DBN，Yang等[10]在深度自编码(DAE)网络的基础上加入深度长短时记忆网络，对海洋背景噪声、客船、货船3类水声目标进行识别，得到了较好的效果，但该方法在小样本训练集条件下识别性能还需要进一步验证。Chen等[11]对比5种典型的机器学习方法在水声目标识别中的识别效果，并分析了网络模型的特性。这些工作均表明了深度学习可以应用于水声目标识别。

生成对抗网络(GAN)模型是一种基于生成模块与对抗模块的深度学习网络模型，通过两个模块之间的极小极大博弈(Minimax Game)实现对模型的优化，在模型达到纳什均衡[12]时，生成器能够很好地学习到真实数据样本的潜在分布，从而使得判别器无法精准地判定样本的真假性。GAN对于生成式模型具有重要的意义，相对于DBN，GAN只用到了反向传播(BP)算法而不需要复杂的马尔可夫链。相比于DAE网络的优化目标是对数似然的下界而不是似然度本身，GAN是直接从数据的分布距离去进行优化，因此理论上如果判别器训练良好，生成器可以完美地学习到真实数据的分布，即GAN的训练是渐进一致的，而DAE是有偏差的，从而导致在生成的实例质量上DAE比GAN低。

Jin等[13]和Gao等[14]将水声信号的LOFAR谱输入GAN模型中实现目标识别，得到了较好识别效果，但实验中使用了庞大数量的样本进行训练，这对于很多实际水声识别应用而言实现较困难。本文提出的GAN模型首先预训练生成模块和对抗模块，然后对带标签样本进行监督训练来优化整个网络的参数，以便在小样本训练集中得到较好的识别效果。

本文首先介绍所提出的GAN模型，利用可视化方法对GAN模型的分类效果进行分析，并与DBN模型和DAE网络模型进行比较；然后用实测水声数据验证GAN模型在目标识别中的效果，并与DBN、DAE等方法进行对比分析。

1 生成对抗网络模型

经典的生成对抗网络模型基于博弈思想，包含生成模型与判别模型两部分，生成模型与判别模型可以由深度神经网络构成。随机噪声z经由生成模型变换得到与真实样本相同长度的序列z′，再交由判别模型去判定样本的真假性。判别模型最终输出一个介于(0，1)之间的数：当判定输入样本为真时，模型输出接近1的值；判定输入样本为假时，模型输出接近0的值。网络优化两个目标：1)判别模型对于样本的真假性尽量判断准确；2)生成模型尽量生成足以造成判别模型判断失误的假样本。因此GAN模型的目标函数定义为

Ez～pz(z)[lg(1-D(G(z)))]，

(1)

式中：V(D，G)表示生成对抗网络模型函数；D、G表示判别模型和生成模型；Ex～pd(x)表示真实数据经过判别器以后取对数的期望值，x～pd(x)表示x服从真实数据分布；D(x)表示判别模型的输出；Ez～pz(z)表示随机数据经过生成器、判别器以后取对数的期望值，z～pz(z)表示z服从随机生成的样本分布，本文方法中z服从高斯分布；G(z)表示生成模型的输出。下面将该目标函数拆成两项，分别讨论判别模型与生成模型的优化问题。

对判别模型D进行优化时，固定生成模型G的参数。当样本来源于真实样本集时，判别模型D(x)需尽量接近于1；当样本来源于生成模型生成的假样本集时，判别模型D(G(z))需尽量接近于0，即1-D(G(z))接近于1，故判别模型目标函数为

Ez～pz(z)[lg(1-D(G(z)))].

(2)

对生成模型G进行优化时，固定判别模型D的参数。生成模型的目标函数只有一个，判别模型D在判定生成样本z′的真假性时，使其输出为真，即D(G(z))趋近于1，1-D(G(z))趋近于0.故生成模型目标函数为

(3)

GAN能够学习原始真实样本集的分布，无论数据分布的复杂性多高，理论上只要GAN训练得足够好，便可以学习。利用GAN的生成对抗特性，在经典GAN上做出改进，使其不仅能够判别样本的真伪，还能够对样本的类别进行判断。

用于识别的GAN模型由两部分组成，生成模型和判别模型。随机噪声z进入生成模型中，生成一组与输入相同大小的序列，该序列与真实的有标签样本、真实的无标签样本分别作为判别模型的输入，判别模型输出3组不同的结果，具有C类的真实样本，在判别模型的输出中可以表示为C+1类。完整模型如图1所示。

图1 GAN识别模型

模型的目标函数推导如下。

对于判别模型D，目标函数包含两个部分：

1)对于有标签真实数据的监督学习损失Ls，

Ls=-Ex,y～pd(x,y)lg(pm(y|x,y∈{1,…,C}))，

(4)

式中：Ex,y～pd(x,y)表示有标签的真实数据经过判别器以后取对数的期望值，(x，y)～pd(x，y)表示数据(x，y)来源于真实样本；pm(y|x,y∈{1,…,C})表示真实样本属于对应标签的概率。

2)对于无标签真实数据和生成样本的无监督损失Lu，

Lu=-Ex～pd(x)lg(1-pm(y=C+1|x))-

Ez～pz(z)lg(pm(y=C+1|z))，

(5)

式中：pm(y=C+1|x)表示无标签样本属于C+1类的概率；Ez～pz(z)表示随机数据经过生成器、判别器以后取对数的期望值，z～pz(z)表示样本来源于生成模型。将生成样本的标签定为C+1，对于无标记真实样本，只需计算样本不属于第C+1类的概率，即1-pm(y=C+1|x)；对于生成样本，需计算样本属于C+1类的概率，即pm(y=C+1|x)。

监督目标函数和无监督目标函数结合起来，得到判别模型目标函数为

LD=Ls+Lu=

-Ex,y～pd(x,y)lg(pm(y|x,y∈{1,…,C}))-

Ex～pd(x,y)lg(1-pm(y=C+1|x))-

Ez～pz(z)lg(pm(y=C+1|z)).

(6)

无监督与有监督训练的训练过程均在判别器模块，对于生成模型G，目标函数与经典GAN相同，即

LG=Ex～pz(z)(lg(1-D(G(z))))=

Ex～pz(z)(lg(1-pm(y=C+1|z))).

(7)

训练中使用交叉熵作为损失函数，利用梯度下降算法优化交叉熵，由于交叉熵使用Sigmoid函数，在训练过程中容易引起梯度消失现象，为了避免梯度消失现象[15]，将目标函数做如下改进：

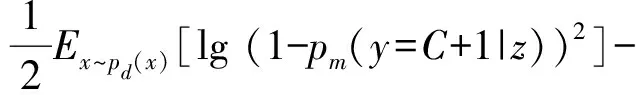
(8)

(9)

2 基于实测水声数据的实验验证

实验过程基于3类实测水声数据，每类标签上有相同的样本数量，每一类数据包含15个水声片段，每一个水声片段时长约10 s左右。实验中，DBN模型、DAE模型与GAN模型均输入分帧以后的水声时域信号，分帧的帧长为10 ms，帧间重叠5 ms.数据集包含1 785个样本数据，其中300个无标签样本数据，1 485个有标签样本数据。有标签样本数据为3类水声数据，每一类495个样本，分别从每一类水声数据中随机选取一段相同长度的数据，其频谱图如表1所示。由表1可知：第1类水声数据的能量集中在0～100 Hz和300～1 000 Hz；第2类水声数据的能量集中在500 Hz左右；第3类水声数据的能量比较分散，在0～100 Hz与1 000 Hz附近的频段上都有较强的能量分布。

表1 输入水声数据的频谱图

2.1 可视化分析实验

用于识别的GAN模型包含生成模块和判别模块。生成模块由卷积层与全连接层组成，对卷积层的16个滤波器进行随机初始化，滤波器大小为1×32，步长为1，滤波器可以反映不同的水声结构特征。生成模块由3个卷积层组成，滤波器个数分别为64个、128个、800个，3层网络的滤波器大小均为1×4，步长为4.判别模型由单层卷积神经网络构成，滤波器个数为16，大小为1×4，步长为4.训练采用循环训练方法，每一次循环随机选取1 485个样本中的600个样本作为训练集，其余为测试集，每次迭代过程中每个样本点只有一次被划入训练集或测试集的机会，对生成对抗模型进行训练，训练的学习率为0.001，根据多次训练的经验，训练迭代终止条件为误差值的差小于0.000 4.训练过程分为两部分：第1部分用真实的有标签数据与无标签样本训练判别模型，将无标签数据标记为C+1类；第2部分训练生成模型，生成器生成数据的分布接近分类器中的C类时输出为0，否则输出为1.训练循环1 000次，训练集与测试集的误差曲线如图2所示。由图3可知，误差在小范围内有抖动，大范围内呈现下降趋势。GAN模型可以认为是一种非参数的产生式建模方法，如果鉴别器训练良好，则生成器可以对数据的联合分布进行建模，生成器数据与无标签样本数据的分布相似。

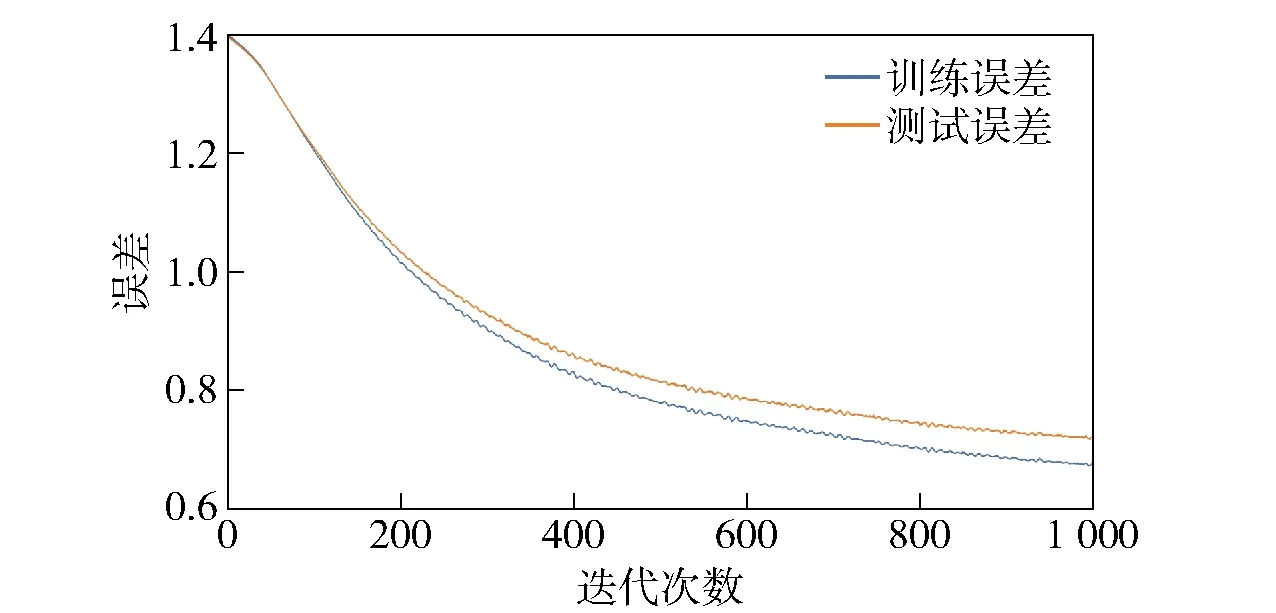
图2 误差曲线

图3 GAN网络层输出的t-SNE特征可视化图形

GAN模型是以判别模型的输出作为分类的特征向量，由于判别模型只有一层输出，所以判别模型只有一层的输出特征，如图3(a)所示，图中t-SNE表示t分布随机领域嵌入算法。为了在三维图中的不同视角下观察分类结果，实验中多角度、多方向旋转图3(a)，选择其中的3幅图形，如图3(b)、图3(c)、图3(d)所示。由图3可知，GAN模型能很好地分离出不同类型的特征数据。

DAE网络模型采用分层训练的方式进行预训练，训练的学习率取0.1，模型的参数采用随机初始化。网络由4个全连接层组成，每一个全连接层做一次有监督训练，将上一个全连接层的特征提取单元作为下一个全连接层的输入。每一个全连接层单独训练以后，对整个网络进行微调，微调时将网络最后一层分类结果与原始样本的标签求交叉熵作为BP算法的优化依据，对整个网络的参数进行优化。其中，第1层网络的输入节点为199，第2层网络的输入节点为150，第3层网络的输入为100，第4层网络的输入节点为80，输出节点为样本类别数3.

图4展示了与图3(a)在相同视角下每一个全连接层提取的特征经过t-SNE降维以后的结果以及第4个全连接层微调后的特征经过t-SNE降维以后的结果。图4给出了DAE模型各个全连接层的输出特征，展示了每一层对不同水声结构特征的提取效果，最后经过微调以后的特征可以很好地分离出3类不同特征。

图4 DAE网络层输出的t-SNE特征可视化图形

DBN网络模型由输入层和3个隐含层和输出层组成，其中输入节点为199，3个隐含层节点数分别为100、50和20，输出层节点数为样本类别数3.每相邻两层组成受限玻尔兹曼机(RBM)网络，首先分别对3个RBM网络进行训练，由于RBM的每一层网络单独训练时采用无监督学习方法，最后应用BP算法对整个网络进行微调，微调的过程将网络最后一层分类结果与原始样本的标签求交叉熵作为BP算法的优化依据，对整个网络的参数进行优化。图6分别给出了DBN中每层网络经t-SNE降维后的结果。由于RBM网络是一种无监督的能量概率模型，t-SNE的输出图形描述了t分布于距离之间的非线性映射，3类水声数据在通过概率模型训练以后会出现在一条线上。图5(b)、图5(c)、图5(d)的逐步变化表示在训练的过程中，相同类型的点在逐步聚集。

对比图3、图4、图5可知：GAN模型对不同类型的样本聚合度优于DAE模型与DBN模型；DAE模型与DBN模型微调后的输出，不同类型之间均有交叉点，DBN模型的交叉点最多。

图5 DBN网络层输出的t-SEN特征可视化图形

为了说明3类方法的有效性，对原始数据数据做t-SNE可视化分析，图6所示为不同视角下3类输入数据应用t-SNE降维后的效果图。由图6可知，原始数据的可分性较差，应用深度学习算法对数据特征进行有效提取后，数据的可分性有了明显提高。

图6 原始数据的 t-SNE特征可视化图形

2.2 识别率对比实验

进一步用GAN模型对3类实测水声数据进行识别，识别率为识别正确的帧数除以总帧数。选取895个随机样本作为训练集，其余样本做测试，所有实验均重复5次，然后取平均值。GAN模型、DBN模型、DAE模型以及MFCC+softmax分类方法的识别结果如表2所示。

由表2可知，基于深度学习的识别效果优于传统MFCC+softmax方法，其中，GAN识别率高于DBN与DAE网络训练的结果。就识别率而言，本文提出的GAN方法明显优于现有的方法。

表2 识别结果

2.3 不同训练样本数量的识别率对比实验

为了进一步分析小样本条件下的识别性能，分别取895、600、300个样本作为训练集，对GAN、DBN、DAE模型进行训练，识别实验结果如表3所示。

由表3中结果可知，当训练样本减少时，DAE网络与DBN识别率随着样本数下降而减小，而GAN的识别率相对较高且比较稳定。在样本数为600时，GAN的识别率达到最优，这表明GAN在小样本范围内存在一个最优样本数匹配，因此，更适合小样本数据的训练与识别。

表3 不同样本数量的识别结果

2.4 模型泛化能力对比实验

实际水声目标识别中，数据集失配是常态，已拥有的数据与待测试的数据在分布上往往是不同的，能否在数据失配情况下获得较好的识别效果是衡量网络模型对水声数据泛化能力的重要指标。本实验分别分析GAN模型与DAE网络模型、DBN模型在数据集失配下的识别能力。实验分为两组：第1组仅对训练集加入不同信噪比的噪声，研究在训练数据质量较差(带噪样本)情况下训练网络模型，并对质量较好的测试数据(干净样本)的识别能力；第2组仅对测试集加入不同信噪比的噪声，研究在训练集数据较为纯粹的情况(干净样本)下训练网络模型，模型是否能够针对含噪声量较大的数据(带噪样本)具有很强的识别能力。

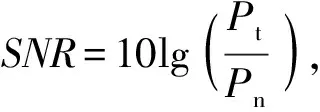
本文实验研究了分别对训练数据与测试数据加噪声，信噪比范围在-20～20 dB时GAN、DAE网络以及DBN的识别能力。图7描述了用不同信噪比的训练数据分别训练3种网络模型，测试每种网络模型对不加噪声测试数据的识别能力。图8描述了用不加噪声的训练数据分别训练3种网络模型，测试网络模型对不同信噪比下的测试数据的识别能力。

图7 训练集加噪声的识别结果对比图

图8 测试集加噪声的识别结果对比图

由图7和图8可以看出：

1)3种网络的识别率均随着训练集信噪比的增加而增大，在信噪比范围内，GAN的识别率始终高于DAE网络与DBN，并且在信噪比-10～20 dB范围内，识别率的变化相比于DBN和DAE也更加平稳。

2)对训练数据加入不同的信噪比时，GAN在信噪比为20 dB时便与不加噪声时的结果相当，而DAE网络与DBN在实验范围内未能达到与无噪声时相当的结果，这表明GAN在提取特征时能够自适应的优化特征提取模型参数，从而能够在信噪比较高时，达到与无噪声时识别正确率相当的结果。

3)对测试数据加噪声时(见图8)，3种网络的识别率均随着训练集信噪比的增加而增大，其中GAN的识别率在整个信噪比范围内显著高于其他两个网络。测试集信噪比低于0 dB时，DAE网络与DBN的识别率迅速下降，且在信噪比低于-5 dB时，识别率下降到33%左右，随着信噪比的进一步减小识别率没有明显的变化；而GAN的识别率随着测试集信噪比的减小平稳下降。图8表明GAN可以在干净的样本中学习到样本的内在特征，从而在遇到加入低信噪比的样本时，依然可以识别样本的类型，网络的泛化能力较好。

3 结论

本文提出一种基于GAN的水声目标识别方法，在实测数据验证实验中将其与另外两种深度学习方法进行了比较。所得主要结论如下：

1)本文方法从可视化的分类效果，小样本的识别率以及系统在数据失配条件下的鲁棒性均优于另外两种识别方法。

2)实验结果表明GAN网络对水声目标信号的分类识别更为有效。

考虑GAN的生成网络与对抗网络是由卷积网络组成，卷积层数量与每一层卷积核的选取都会影响GAN的识别率，因此，后续还将进一步研究在不同实测数据集中，网络参数对识别率的影响。

参考文献(References)

[1] PARK J，JUNG D J.Identifying tonal frequencies in a lofargram with convolutional neural networks[C]∥Proceedings of the 2019 19th International Conference on Control，Automation and Systems.Jeju，Korea: IEEE，2019:338-341.

[2] ZHANG J M，DING Y Y.Underwater target recognition based on spectrum learning with convolutional neural network[C]∥Proceedings of the IEEE 5th Information Technology and Mechatronics Engineering Conference.Chongqing，China: IEEE，2020:1520-1523.

[3] 江伟华，童峰，王彬，等.采用主分量分析的非合作水声通信信号调制识别[J].兵工学报，2016，37(9):1670-1676.

JIANG W H，TONG F，WANG B，et al.Modulation recognization method for non-operation underwater acoustic communication signals using principal component analysis[J].Acta Armamentarii，2016，37(9):1670-1676.(in Chinese)

[4] ZENG X Y，LU C Y，LI Y.A multi-task sparse feature learning method for underwater acoustic target recognition based on two uniform linear hydrophone arrays[C]∥Proceedings of INTER-NOISE and NOISE-CON Congress and Conference Proceedings.Seoul，Korea:IEEE，2020:4404-4411.

[5] 王强，曾向阳.深度学习方法及其在水下目标识别中的应用[J].声学技术，2015，34(2): 138-140.

WANG Q，ZENG X Y.Deep learning methods and their applications in underwater targets recognition[J].Technical Acoustics，2015，34(2):138-140.(in Chinese)

[6] LIS C，JIN X，YAO S B，YANG S Y.Underwater small target recognition based on convolutional neural network[C]∥Proceedings of Global Oceans 2020: Singapore-U.S.Gulf Coast.Biloxi，MS，US:IEEE，2020.

[7] HUANG S Z，XU H S，XIA X Z.Active deep belief networks for ship recognition based on BvSB[J].Optik，2016，127(24):11688-11697.

[8] SHENG S，YANG H H，SHENG M P.Compression of a deep competitive network based on mutual information for underwater acoustic targets recognition[J].Entropy，2018，20(4)：243-256.

[9] XIE J W，CHEN J，ZHANG J.DBM-based underwater acoustic source recognition[C]∥Proceedings of 2018 IEEE International Conference on Communication Systems.Chengdu，China: IEEE，2018: 366-371.

[10] YANG H H，XU G H，YI S Z，et al.A new cooperative deep learning method for underwater acoustic target recognition[C]∥Proceedings of OCEANS 2019.Marseille，France: IEEE，2019.

[11] CHEN Y C，XU X N.The research of underwater target recognition method based on deep learning[C]∥Proceedings of 2017 IEEE International Conference on Signal Processing，Communications and Computing.Xiamen，China:IEEE，2017.

[12] DEUTSCH Y.A polynomial-time method to compute all nash equilibria solutions of a general two-person inspection game[J].European Journal of Operational Research，2021，288(3):1036-1052.

[13] JIN G G，LIU F，WU H，et al.Deep learning-based framework for expansion，recognition and classification of underwater acoustic signal[J].Journal of Experimental & Theoretical Artificial Intelligence，2020，32(2):205-218.

[14] GAO Y J，CHEN Y C，WANG F Y，et al.Recognition method for underwater acoustic target based on DCGAN and DenseNet[C]∥Proceedings of the IEEE 5th International Conference on Image，Vision and Computing.Beijing，China:IEEE，2020:215-221.

[15] PASCUAL1 S，BONAFONTE1 A，SERRJ.SEGAN: speech enhancement generative adversarial network[C]∥Proceedings of the 18th Annual Conference of the International Speech Communication Association.Stockholm，Sweden: International Speech Communication Association，2017:3642-3646.