基于正交基函数的矢量磁梯度异常探测

马剑飞，颜冰，林春生

(海军工程大学 兵器工程学院，湖北 武汉 430033)

0 引言

磁异常探测技术具有不受空气、海水、泥沙、土壤等介质影响的优势，在勘探矿物、航空反潜以及未爆弹探测等方面具有广泛而深入的应用，其作为一种被动探测技术具有隐蔽性好的特点[1-3]。

目前主要的标量磁异常探测技术大致分为两类:第一类是目标磁模型正交基函数(OBF)与测量信号乘积的积分方法。文献[4]提出以磁偶极子为模型的标量OBF检测器，该方法基于磁偶极子模型并结合目标与测量系统的相对运动信息对信号进行正交基分解，适用于隐蔽磁性目标的检测；文献[5]提出了以线列阵偶极子为模型的主成分检测器，该方法的OBF是在特定距离条件下仿真计算得到，不适用于对未知距离条件下的目标检测。第二类是基于信号和噪声统计特性不同的检测方法，包括最小熵检测器(MED)[6]以及高阶过零检测器[7]，这类方式相对于OBF检测器具有计算量较小的优点，但需要对环境噪声进行长时间的统计特性分析，而且检测能力比较有限。在实际的地磁环境中，噪声功率谱一般为1/fα结构(f表示信号频率，α表示功率谱衰减常数)，文献[8]以自回归(AR)模型白化滤波器对环境噪声以及OBF进行了校正，该方法在1/fα环境噪声条件下相比于OBF检测器取得了更优的检测结果，但是求解AR模型白化滤波器需要对噪声进行长时间的统计特性分析，也要求噪声是平稳的，但实际的测量难以满足这一条件。

目前主要的磁性目标远程探测方法主要是基于磁标量或者标量磁梯度的测量，标量测量所获取的目标磁场信息较为有限，不能从磁场信息的角度充分解释目标；矢量磁测量虽然可以提高对目标磁场信息的解释能力，但地磁场相对于磁性目标产生的磁异常为强磁场，测量平台轻微的晃动就会导致矢量磁传感器输出产生很大的变化。

随着超导磁力仪技术的发展，基于矢量磁梯度的磁异常探测方式愈发受到重视[9-10]。矢量磁梯度相对磁标量探测以及磁矢量探测的优势在于：1)测量结果当地磁倾角和地磁偏角无关；2)具有更丰富的磁场信息，可以利用几个测量点的磁梯度张量快速反演目标的位置和磁矩[11-13]；3)具备很强的共模抑制能力，特别是当测量平台晃动时，测量值可以有效避免地磁场和背景磁场噪声影响[14]；4)日变效应会导致假的磁异常，需要使用额外的基站进行校正，磁梯度张量不受日变效应影响，自然环境的磁梯度一般小于0.02 nT/m，而且在一个区域内的值相对稳定[15]。

在磁梯度OBF探测算法层面，文献[4]提出了一种基于5个正交基的标量磁梯度OBF检测方法，该方法能够有效消除环境磁噪声的影响，可以显著提升检测的信噪比。文献[16]在此基础提出了一种基于4个正交基的标量磁梯度OBF检测方法，该方法消耗更小的计算资源，而且具有更好的鲁棒性，限制条件是目标与系统之间距离大于磁梯度阵列基线长度的3倍(一般情况下此条件是很容易满足的)。文献[17]进一步研究了消除观测信号趋势和偏差的方法，并评估了观测窗长度对算法性能的影响，发现当观测窗长为最近点(CPA)距离的1～4倍时，算法的检测性能相对于最优窗长(2～2.5倍CPA距离)的检测性能不会发生明显下降。

本文旨在研究一种基于矢量磁梯度测量的磁性目标远程探测技术，可以在低信噪比条件下能够提高提升探测的稳定性(降低检测虚警率)以及准确估计目标的位置参数和磁矩参数。

1 OBF检测器

1.1 传统的磁标量OBF检测器

当探测距离大于2.5倍磁性目标长度时，磁性目标可以视为一个磁偶极子[18]，此时距离磁性目标r处的磁场矢量B可以表示为

(1)

式中：μ0为空间磁导率，μ0=4π×10-7H/m；M表示目标磁矩矢量；r表示磁性目标到传感器的位移矢量r的模值。当B≪T时(T表示地磁场矢量)，标量磁场S的测量可视为磁场矢量在地磁场方向上的投影，即

(2)

图1所示为运动载体沿直线运动时与磁性目标(目标视为偶极子)的相对几何关系。图1中，坐标原点O表示目标的位置(偶极子)，X轴表示运动载体沿直线运动的方向，Y轴表示运动载体的左舷方向，Z轴表示竖直向上方向，R0表示传感器和磁性目标之间的CPA距离，D0表示传感器当前位置和CPA点之间的距离，θM表示目标磁矩方向与Z轴的夹角，θT表示地磁场方向与Z轴的夹角，φM表示目标磁矩矢量在OXY面的投影与X轴的夹角，φT表示地磁场方向在OXY平面的投影与X轴的夹角。

(1)式代入(2)式，标量磁场可表示为基函数φ(ω)的加权和形式：

(3)

对基函数φ(ω)进行施密特正交化，可得

(4)

图2所示为磁偶极子模型对应的正交基函数f1(ω)、f2(ω)与f3(ω)。

图2 正交基函数

由(4)式可知，正交化系数aj*可通过OBF与测量信号乘积的积分进行解算：

(5)

对(5)式离散化处理，可得能量系数

(6)

式中：Δω表示空间采样长度，Δω=ωi+1-ωi，ωi表示i时刻X轴方向距离与CPA距离的比值，i的取值范围为[-k,k]。在[ω-k,ωk]观测窗区间内，信号的能量Eb可以表示为能量系数的平方和

(7)

1.2 磁矢量OBF检测器及性能分析

当目标磁场远小于地磁场时，磁标量的测量可等效于目标磁场矢量在地磁场方向上的投影，同理三分量磁场的测量SX、SY和SZ也可以看作是目标磁场在X轴、Y轴和Z轴方向上的投影。以磁矢量测量SX为例，结合(3)式可知

(8)

式中：bX,j为分量SX对应的基函数系数，bX,1=3sinθM·cosφMsinθXcosφX，bX,2=3(cosθMsinθXcosφX+sinθMcosφMcosθX)，bX,3=3cosθMcosθX，bX,4=-sinθM·sinθXcos(φM-φX)-cosθMcosθX，θX表示矢量磁力仪X轴方向与坐标系Z轴的夹角(θX=π/2 rad)，φX表示矢量磁力仪X轴方向与坐标系X轴的夹角(φX=0 rad)。在[ω-k,ωk]的观测窗区间内，X轴方向的OBF能量检测器为输入信号的OBF加权能量：

(9)

式中：αX,j*为分量SX对应的能量系数。

同理，也可以构造Y轴方向的OBF检测器EY以及Z轴方向的OBF检测器EZ，则矢量OBF能量检测器的输出可以构造为

Ev=EX+EY+EZ.

(10)

下面以X轴的分量SX为例(无晃动条件下与磁标量测量等效)，推导OBF检测结果所服从的概率分布并对检测性能的影响因素进行分析。

假设X轴测量的环境噪声服从高斯独立同分布SX(ωi)～N(0,σ2)，σ为高斯噪声的标准差，代入(6)式可得

(11)

由于

(12)

故

αX,j*～N(0,σ2Δω).

(13)

进一步有

(14)

下面证明αX,1、αX,2和αX,3之间相互独立，以αX,1和αX,2为例，αX,1和αX,2的期望分别为

E(αX,1)=0，E(αX,2)=0，

(15)

αX,1和αX,2乘积的期望为

(16)

又因为

(17)

故

E(αX,1αX,2)=0，

(18)

E(αX,1αX,2)-E(αX,1)E(αX,2)=0.

(19)

由高斯分布相互独立的充要条件可知，αX,1、αX,2和αX,3之间相互独立，联立(14)式，可得

(20)

由卡方分布的性质可知，X轴测量噪声经过OBF加权后其能量的期望EX,n和方差DX，n分别为

(21)

(22)

进一步，综合(9)式和(21)式可知，噪声OBF加权能量与信号OBF加权能量的比值可表示为

(23)

式中：EX为X轴测量的信号能量；η越小，表示信号与噪声的区分度越高。

联立(9)式、(21)式可知，信号OBF检测能量仅与信号本身的能量相关，而高斯噪声的OBF检测能量却与空间采样长度有关，因此空间采样长度Δω越小则OBF检测器对噪声和信号的区分度越高。另外由(22)式可知，空间采样长度越小则同分布噪声经过OBF检测器后概率分布的方差越小。因此不难得出结论：1)在同样测量环境条件下，空间采样长度越小则OBF检测器对环境噪声和目标信号的区分越明显；2)空间采样长度越小则检测器的稳定性越好。

假设三轴测量的噪声服从独立同分布且三轴测量的信号能量相同，对于矢量检测器而言，

(24)

(25)

式中：En和Dn分别为矢量检测器噪声经OBF加权后其能量的期望和方差。则矢量检测器的噪声OBF加权能量En和信号OBF加权能量Ev的比值为

(26)

由(26)式可以看出，在同等空间采样长度条件下，矢量测量相对于标量检测并不能改变区分度，但联立(22)式和(25)式可得

3D

En=DX,n/EX,n.

(27)

1.3 磁梯度OBF检测器

鉴于矢量磁梯度测量兼具磁标量检测的抗晃动性以及磁矢量检测信息丰富的优势，据此在传统标量磁梯度OBF检测器的基础之上提出了一种矢量磁梯度OBF检测器，该算法可在低信噪比以及平台晃动条件下可靠检测磁性目标，并能够反演得到目标的矢量磁梯度信号。文献[16]提出了一种基于4个OBF的标量磁场梯度的OBF检测器，标量磁梯度测量等效于磁场矢量在地磁场方向上投影的差分G，即

(28)

式中：Br+ΔZ为距离磁性目标r+ΔZ处的磁场矢量；Br为距离磁性目标r处的磁场矢量。

磁梯度传感器由两个相距ΔZ的磁传感器构成，图3所示为磁梯度传感器沿直线运动时与磁性目标(目标视为偶极子)的相对几何关系，其中X轴为运动载体沿直线运动的方向，Y轴为运动载体的左舷方向，Z轴为竖直向上方向，R0为传感器和磁性目标之间的CPA距离。

图3 磁梯度传感器与目标的相对运动关系

标量磁梯度的正交基形式为

(29)

图4 磁梯度正交基函数

(30)

标量磁梯度检测器的输出Es可表示为能量系数的平方和，

(31)

记矢量磁梯度的三分量分别为GZ,X、GZ,Y和GZ,Z，结合矢量磁场OBF检测器的推导过程可知，矢量磁梯度OBF检测器的输出可以构造为矢量磁梯度三分量对应能量系数的平方和形式

(32)

由(27)式可知，矢量磁梯度OBF检测器相比于标量磁梯度OBF检测器改善了检测的稳定性，矢量OBF检测器反演的磁梯度信号可以表示为

(33)

2 磁性目标参数估计

反演的磁梯度信号虽然相比于原始的测量信号在很大程度上提高了信噪比，但受检测器窗长以及噪声非严格高斯等因素的影响，反演信号相较于真实信号产生了一定的畸变。注意到由目标产生的信号是可通过偶极子模型进行拟合的，而信号畸变的部分则不可以，因此可以通过偶极子模型对反演信号进行拟合从而实现对目标磁矩参数和位置参数的估计。

以磁性目标中心为原点建立坐标系，X为运动载体沿直线运动的方向，Y为运动载体的左舷方向，Z为竖直向上方向，磁性目标等效于单偶极子模型，设磁传感器l的坐标为(xl，yl，zl)，则i时刻磁传感器l的测量为

(34)

式中：MX、MY和MZ分别表示目标在X轴方向、Y轴方向和Z轴方向的磁矩；磁偶极子系数的计算系数分别为

bX,i,l=aY,i,l，cX,i,l=aZ,i,l，cY,i,l=bZ,i,l，

Fi·M=ΔBi=Bi,1-Bi,2，

(35)

式中：

进一步，联立N个测量点的磁梯度信号接收模型，可得

F·M=ΔB，

(36)

式中：F=[F1;F2; …;FN]；ΔB=[B1,1-B1,2;B2,1-B2,2; …;BN,1-BN,2].

显然，(36)式中的方程个数为3N，G的列数为3.磁性目标参数估计问题可表示为

(37)

式中：U为估计向量。

由于载体做直线运动且各测量点在X轴方向的相对坐标为已知参数，故U=[YCPA,ZCPA,MX,MY,MZ]。当N>1时测量模型为超定方程组，利用最小二乘法求解(36)式可得

M=F+ΔB，

(38)

式中：F+为F的M-P广义逆矩阵，由于F是列满秩矩阵，F+存在且唯一，

F+=(FTF)-1FT.

(39)

(39)式代入(37)式，磁性目标参数估计问题可转换为

(40)

式中：I为单位矩阵；U=[YCPA,ZCPA].(40)式是一个典型的多变量优化问题，相比于(37)式表述的优化模型，其估计的向量维数由5维降到了2维，极大地降低了算法的运算量。

粒子群优化[19](PSO)算法是一种群体智能优化算法，算法中的每个粒子都代表一个问题的潜在解，粒子速度决定了粒子移动的方向和距离，速度随自身和其他粒子的移动经验进行动态调整，从而实现个体在可解空间内的动态寻优，故采用PSO算法能够解算(40)式表述的多变量优化问题。估计向量U代入(38)式可以得到目标的磁矩参数，进一步将位置参数和磁矩参数代入偶极子模型，可得到磁性目标的拟合信号，而且磁拟合信号的能量就可以作为区分目标信号和噪声的检测量。

3 仿真实验

设磁性目标的中心为空间直角坐标系的原点，X轴与平台的轴线重合并指向平台的艏部，Y轴指向左舷，Z轴竖直向上。仿真条件设置为：初始时刻目标的位置为(-200 m，-50 m，5 m)；目标的磁矩为(-3×103A·m2,1×103A·m2,5×103A·m2)，磁梯度张量系统测量基线的尺寸为0.5 m；空间采样长度为0.1 m；观测窗区间为[-2R0,2R0]。下面分5个层面对本文算法的性能进行仿真实验验证。

3.1 与传统检测方法性能的对比

图5(a)和图5(b)所示分别为信噪比为6 dB和-6 dB时，磁标量OBF检测器、传统的特征值检测方法和MED检测方法的检测性能对比，此处的信噪比定义为

(41)

式中：Amax表示信号的峰值。OBF检测器和特征值检测器的凸出峰值越突出，表示检测的区分度越大；MED检测器向下的峰值越明显，表示此时的信息熵越小，即检测的区分度越大。在图5(a)和图5(b)中，可以看出在高信噪比条件下，3种检测算法都能准确检测目标，但OBF检测性能更加稳定而且具有更高的检测信噪比；在低信噪比条件下，特征值检测方法与MED检测方法皆已失效，此时OBF检测器可以准确检测目标，而且仍然具有较高的检测信噪比。

图5 标量OBF检测器与传统检测方法性能的对比

3.2 空间采样长度对OBF检测器的影响

图6(a)和图6(b)所示分别为信噪比为-6 dB和-12 dB时，空间采样长度为0.1 m、0.2 m以及0.5 m时所对应的磁标量OBF检测器性能。从图6中可以看出，在同等信噪比条件下，空间采样长度越小，则检测的信噪比越高而且检测的波动性越小，此结果与1.2节中“空间采样长度越小，则信号与噪声区分越明显以及检测稳定性越好”的理论证明是一致的。

图6 空间采样长度对标量OBF检测器性能的影响

3.3 矢量与标量OBF检测器对比

图7(a)和图7(b)所示为空间采样长度为0.1 m、信噪比分别为-6 dB和-12 dB时的标量OBF和矢量OBF检测器性能比较，从中可以看出在没有目标时矢量OBF的检测曲线的波动性较小，具有更稳定的检测性能，此结果与1.2节中“矢量OBF检测器相对于标量OBF检测器的优势是改善了标量检测的稳定性”的理论证明是一致的。

图7 标量和矢量检测器性能对比(空间采样长度0.1 m)

然而受地磁场的影响，当矢量磁传感器发生轻微晃动时，其输出就会产生较大的变化，晃动幅值为0°、0.01°和0.1°时的矢量OBF检测器性能如图8所示，轻微的晃动都会导致检测器性能发生恶化，当晃动幅值达到0.1°时，矢量OBF检测算法已经失效。

图8 矢量磁力仪晃动对矢量OBF检测器性能的影响

3.4 磁梯度OBF检测器的抗晃动性

图9(a)、图9(b)、图9(c)、图9(d)分别为信噪比为-6 dB和-12 dB时，矢量磁梯度OBF检测器与标量磁梯度OBF检测器的性能比较，从中可以看出在同等信噪比和空间采样长度条件下，当没有目标时，矢量梯度检测相对于标量梯度检测的波动要小得多，即矢量梯度检测具有更低的虚警率，此结果符合1.2节中“矢量OBF检测器相对于标量OBF检测器的优势是改善了标量检测的稳定性”的结论。

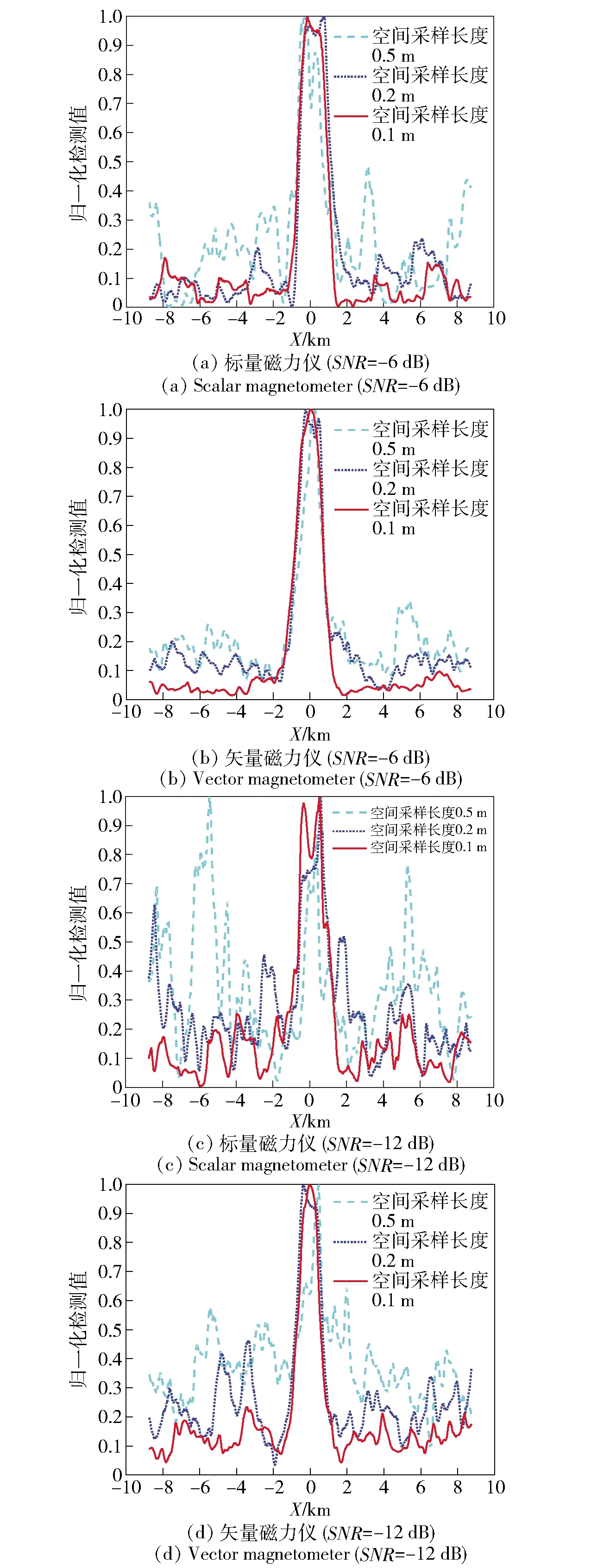
图9 标量和矢量磁梯度OBF检测器性能对比

图10所示为-6 dB信噪比时不同晃动角度对应的磁梯度矢量OBF检测曲线，从中可以看出在10°晃动角以下，算法的性能没有发生明显的变化，仍然保持较高的检测信噪比。通过与磁标量OBF检测器、磁矢量OBF检测器以及磁梯度标量检测器进行对比，可以发现矢量磁梯度OBF检测器既可以探测到更丰富的目标磁信息，同样也具有较好的抗晃动性能。

3.5 目标磁矩和位置参数估计

在信噪比为-12 dB、晃动幅度为1°时，PSO算法优化前后的检测性能对比如图11所示。由图11可以看出：PSO算法优化后的检测具有更高的信噪比；PSO优化前的峰值持续约为50 m，而PSO优化后其检测峰值更为尖锐，与真实CPA点在X轴方向的距离仅为3 m，意味着PSO优化后的检测器能够给出更为准确的目标范围。

图11 PSO优化前后检测性能对比(SNR=-12 dB，晃动幅度1°)

表1所示为基于矢量磁梯度OBF检测器的反演信号，利用PSO算法估计得到的目标位置参数与磁矩参数，可以看出该算法在-12 dB信噪比条件下，对目标的位置参数以及磁矩参数的估计误差皆小于20%.

表1 位置和磁矩参数估计结果

综上所述，磁梯度OBF检测方法可以克服平台晃动的影响以及提供丰富的目标磁场信息，与PSO优化算法相结合，不但能够提升进一步检测的信噪比，而且可以在低信噪比条件下准确估计目标的位置参数和磁矩参数，可应用于远程探测磁性目标与确定目标的搜索范围。

4 实测试验

图12所示为午夜时分在某消磁实验室进行的探测试验，磁梯度测量系统为4个传感器呈十字型布置的Mag-03磁通门传感器，采集设备为HIOKI高精度24位AD采集系统，受试验条件限制，探测的目标为一个运动的制式灭火器(几何尺寸与一般的未爆弹相近)，磁梯度测量的噪声标准差约为0.2 nT/m.

图12 高精度磁梯度测量

图13所示为HIOKI高精度采集系统采集的磁性目标磁梯度信号，其中GY,X、GY,Y和GY,Z分别表示矢量磁信号在Y轴方向上的梯度，磁梯度系统与磁力仪目标的CPA距离为1.2 m。图13中可以明显观测到目标的通过特性曲线，不适合检验算法在低信噪比条件下的检测性能。

图13 HIOKI高精度采集系统测量的磁梯度信号

为进一步检验算法的性能，如图14所示，中午时分在某院的小树林进行磁性目标磁梯度探测试验，AD采集设备为16位NI USB-6216采集卡，共进行了6航次测量试验，磁梯度测量的噪声标准差约为65 nT/m.

如图15(a)、图15(b)、图15(c)所示，分别是采样率为5 Hz、50 Hz以及500 Hz时，6个航次的磁梯度OBF检测结果，从中可以看出采样频率越高则检测器的检测能力越强，此结果验证了1.2节中“空间采样长度越小，则信号与噪声区分越明显以及检测稳定性越好”的理论证明。

表2所示为利用PSO磁性目标参数估计算法对目标参数的估计结果，其中位置参数的相对估计误差小于30%，受感应磁场的影响，横向目标的磁矩模值在2 A·m2左右，垂向目标的磁矩在0.3 A·m2左右。

表2 目标参数估计结果

这里通过磁梯度传播衰减理论来推算矢量磁梯度OBF检测器对水雷目标的探测距离(目标磁矩在102A·m2量级)，对比两次试验的磁梯度测量噪声可知，第1次磁梯度测量噪声为第2次测量噪声的1/320，其探测距离同等条件下会增加至之前的4.2倍。由图15可知，当目标磁矩在0.3 A·m2且测量噪声标准差在65 nT/m左右时探测的距离大于2 m，因此当目标磁矩大于100 A·m2且测量噪声标准差在0.2 nT/m左右时，磁梯度OBF检测器的探测距离大于35 m.

图15 不同采样率下矢量磁梯度OBF检测

5 结论

本文针对标量OBF检测器磁场解释性弱的问题以及磁矢量OBF检测器抗晃动性能差的缺点，提出了一种矢量磁梯度的OBF检测器，并分析指出空间采样长度是影响OBF检测器性能的关键因素且矢量OBF检测器相较于标量OBF检测器可以降低检测的虚警概率。得出主要结论如下：

1)OBF检测器相对于传统的检测算法具有更优的检测性能。

2)相对于传统的OBF检测器，矢量磁梯度OBF检测器的优势在于兼具抗晃动性和磁场解释性。

3)矢量磁梯度OBF检测器与PSO目标参数估计算法相结合，可以在低信噪比条件下比较准确地估计磁性目标的位置参数以及磁矩参数。

参考文献(References)

[1] LIN J，WANG M C，ZHAO J.Review: progress in SQUID-based geophysical precision measurement technology[J].Journal of Harbin Institute of Technology(New Series)，2020，27(3):101-115.

[2] ALLEN G I，MATTHEWS R，WYNN M.Mitigation of platform generated magnetic noise impressed on a magnetic sensor mounted in an autonomous underwater vehicle[C]∥Proceedings of MTS/IEEE Oceans 2001.Honolulu，HI，US: IEEE，2001.

[3] ALLEN G I，SULZBERGER G，BONO J T，et al.Initial evaluation of the new real-time tracking gradiometer designed for small unmanned underwater vehicles[C]∥Proceedings of MTS/IEEE Oceans 2005.Washington，DC，US：IEEE，2005.

[4] GINZBURG B，FRUMKIS L，KAPLAN B Z.Processing of magnetic scalar gradiometer signals using orthonormalized functions[J].Sensors and Actuators A: Physical，2002，102(1/2):67-75.

[5] SHEINKER A，MOLDWIN M B.Magnetic anomaly detection(MAD)of ferromagnetic pipelines using principal component analysis(PCA)[J].Measurement Science & Technology，2016，27(4): 045104.

[6] SHEINKER A，SALOMONSKI N，GINZBURG B，et al.Magnetic anomaly detection using entropy filter[J].Measurement Science and Technology，2008，19(4): 045205.

[7] SHEINKER A，GINZBURG B，SALOMONSKI N，et al.Magnetic anomaly detection using high-order crossing method[J].IEEE Transactions on Geoscience & Remote Sensing，2012，50(4):1095-1103.

[8] SHEINKER A，SHKALIM A，SALOMONSKI N，et al.Processing of a scalar magnetometer signal contaminated by 1/fαnoise[J].Sensors and Actuators A: Physical，2007，138(1): 105-111.

[9] SCHMELZ M，STOLZ R，ZAKOSARENKO V，et al.Field-stable SQUID magnetometer with sub-fT Hz-1/2resolution based on sub-micrometer cross-type Josephson tunnel junctions[J].Superconductor Science & Technology，2011，24(6):065009.

[10] SCHMELZ M，ZAKOSARENKO V，CHWALA A，et al.Thin-film based ultralow noise SQUID magnetometer[J].IEEE Transactions on Applied Superconductivity，2016，26(5): 1600804.

[11] 张光，张英堂，李志宁，等.载体平动条件下的磁梯度张量定位方法[J].华中科技大学学报(自然科学版)，2013，41(1): 21-24.

ZHANG G，ZHANG Y T，LI Z N，et al.Localizing method of magnetic field gradient tensor under carriers moving parallelly[J].Journal of Huazhong University of Science&Technology(Natural Science Edition)，2013，41(1):21-24.(in Chinese)

[12] 于振涛，吕俊伟，许素琴，等.运动平台的磁性目标实时定位方法[J].哈尔滨工程大学学报，2015，36(5): 606-610.

YU Z T，LÜ J W，XU S Q，et al.A real-time localization method of a magnetic target based on moving flat[J].Journal of Harbin Engineering University，2015，36(5):606-610.(in Chinese)

[13] 迟铖，任建存，吕俊伟，等.基于磁梯度张量的目标多测量点线性定位方法[J].探测与控制学报，2017，39(5): 58-62，70.

CHI C，REN J C，LÜ J W，et al.Linear localization method based on magnetic gradient tensor of muliti-points[J].Journal of Detection & Control，2017，39(5):58-62，70.(in Chinese)

[14] CHWALA A，SCHMELZ M，ZAKOSARENKO V，et al.Underwater operation of a full tensor SQUID gradiometer system[J].Superconductor Science and Technology，2019，32(2): 024003.

[15] 钟炀，管彦武，石甲强，等.利用IGRF模型计算全张量地磁梯度[J].物探与化探，2020，44(3):582-590.

ZHONG Y，GUAN Y W，SHI J Q，et al.The calculation method of full tensor geomagnetic gradient based on IGRF model[J].Geophysical and Geochemical Exploration，2020，44(3):582-590.(in Chinese)

[16] GINZBURG B，FRUMKIS L，KAPLAN B Z.An efficient method for processing scalar magnetic gradiometer signals[J].Sensors and Actuators A: Physical，2004，114(1):73-79.

[17] FRUMKIS L，GINZBURG B，SALOMONSKI N，et al.Optimization of scalar magnetic gradiometer signal processing[J].Sensors and Actuators A: Physical，2005，121(1):88-94.

[18] 张朝阳，肖昌汉，高俊吉，等.磁性物体磁偶极子模型适用性的试验研究[J].应用基础与工程科学学报，2010，18(5):862-868.

ZHANG C Y，XIAO C H，GAO J J，et al.Experiment research of magnetic dipole model applicability for a magnetic object[J].Journal of Basic Science and Engineering，2010，18(5): 862-868.(in Chinese)

[19] KENNEDY J，EBERHART R.Particle swarm optimization[C]∥Proceedings of the 4th International Conference on Neural Networks.Perth，WA，Australia：IEEE，1995：1942-1948.