弹载图像探测器广域协同探测算法

娄文忠，苏子龙，汪金奎，刘伟桐，赵飞

(北京理工大学 爆炸科学与技术国家重点实验室，北京 100081)

0 引言

作战毁伤效果评估的定义是，在对既定目标进行军事打击(包括致命和非致命)后，对目标进行及时和准确的毁伤估计[1]。基于图像的毁伤评估是战场毁伤评估的主要方法，通过对打击前后目标图像采集，分析目标毁伤前后图像变化特征，可获得直观准确的毁伤效果信息。

由于星载图像探测方式使用权限高、轨道周期长以及机载图像探测方式飞行周期长等缺点，弹载图像探测方式在区域作战的体系对抗中具有巨大潜力。基于弹载的目标毁伤图像捕获技术是作战毁伤信息获取的典型方法[2]。李从利等[3]研究了侦察弹图像质量评价方法，针对弹载侦察图像由于受成像平台和条件限制存在多类型混杂失真,提出了评价方法，为图像后续处理和成像系统性能优化提供了量化依据和指标参考；王正平等[4]针对炮射侦察弹的工作特性,提出了弹道设计方案，建立了炮射段、分离段、减速段弹道模型,推导了开伞时间与分离时间、降落伞面积与弹道末端约束的关系；李卉等[5]研究了电视侦察弹与舰炮武器系统的匹配问题，以武器系统综合作战效能为目标函数进行系统指标优化，对舰炮武器系统作战使用电视侦察系统提供参考。

弹载毁伤图像感知中存在多组约束条件，首先是视场角与评估图像清晰度的约束，视场角越小，获取的图像清晰度越高，但图像靶面上可获取的毁伤区域面积越小；探测到目标的概率可通过仿真及试验制定，是系统的输入参数;弹载图像毁伤评估系统通常不具备巡飞能力，获取毁伤图像信息的窗口窄，系统难以对毁伤过程的全局图像信息感知。多智能体系通过无线信息交联，实现广域视野协同探测，是现代战场中越来越重要的信息获取模式[6]，弹载图像探测器是通过弹药抛撒出多个子弹药，分时分区域获取毁伤图像信息，通过图像的时间拼接与空间拼接，获取大区域范围的高质量毁伤图像信息，可提供战场毁伤图像信息获取的有效解决方案。

1 多约束图像探测器建模

战场目标通常可以分为3种类型，已知固定目标、已知移动目标与临时目标。其中已知固定目标为作战前通过其他途径获取的固定目标，其坐标点已知；已知移动目标虽然可在战前获取，但目标可能在探测过程中移动位置；临时目标指在作战过程中临时发现的高价值目标，其坐标在目标发现后才能获取。本文主要讨论已知固定目标类型，并假定图像子探测器数量与目标数量一致，预设条件如表1所示。

表1 战场与图像探测器预设条件

为准确描述协同控制系统，需要定义以下预设条件：

预设条件1表示作战区域内的多个目标存在重要性差异；为简化系统设计和适应弹载环境，预设条件2、条件3、条件4将图像探测器定义为可完成简易修正，并可快速切换视场的系统模型。图像探测器的控制系统由于系统复杂度和设计成本，通常难以采用舵机等三维修正机构，本文假设图像探测器具备一维修正能力，同时可通过云台控制视线轴方向。修正力沿图像探测器轴线方向，因此探测器均在弹道平面内运动，二维动力学方程[7]表示为

(1)

式中：m为图像探测器质量；v表示图像探测器飞行速度；Fx和Fy分别为探测器的阻力和升力，x、y分别为探测器在弹道平面内的水平位置和垂直位置；g为当地重力加速度；θ为探测器弹道倾角；Jz为探测器对载体坐标系z轴的转动惯量；ωz为绕z轴的转动角速度；Mz为俯仰力矩；ϑ为俯仰角；α为攻角。

在图像探测器上采用增阻式一维弹道修正模型，其攻角为0°和升力为0 N，因此探测器动力学方程可简化为(2)式。

(2)

式中：C为探测器常态飞行下阻力系数，Ci为预设定增阻器开启后的C；ρ为空气密度；S为气动面积；k为放大倍数；ti为预设定增阻器开启时间。通过增阻可改变探测器阻力系数，当增阻器打开时，可认为其气动面积保持不变，阻力系数增大为原来的k倍[8]。

为保证目标不失一般性，面目标可定义为多个点目标构成的集合，表示为T={T1,T2,…,Tn}，其中：n代表探测区域中目标个数；Tj={Xj,sj,Wj},j∈{1,2,…,n}，j代表目标编号，协同探测模型如图1所示；Xj表示点目标的坐标点；sj表示点目标的有效信息面积，在此区域内的图像信息为毁伤评估的有效信息；此外还需对目标区域定义价值系数Wj.

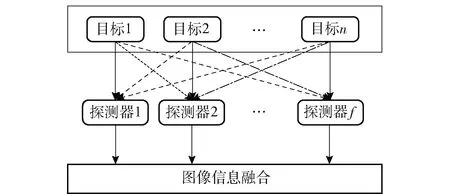
图1 协同探测模型

2 图像探测器探测能力评价准则

通常情况下，有效图像信息量不会随时间线性增长，且随时间增长获取新信息的速度会降低，在文献[6]中采用指数函数定义了在图像覆盖区域内，系统获取的有效信息的收益函数R(t)及收益增量函数ΔR(t)为

R(t)=1-(1-R0)e-λt，

(3)

ΔR(t)=λ(1-R0)e-λtΔt，

(4)

式中：R0表示目标区域内具备的初始信息量；Δt为采样周期；λ为传感器性能指数，即当时间趋于无穷大时，可对该区域实现完全探测，图像探测器探测面积模型如图2所示。

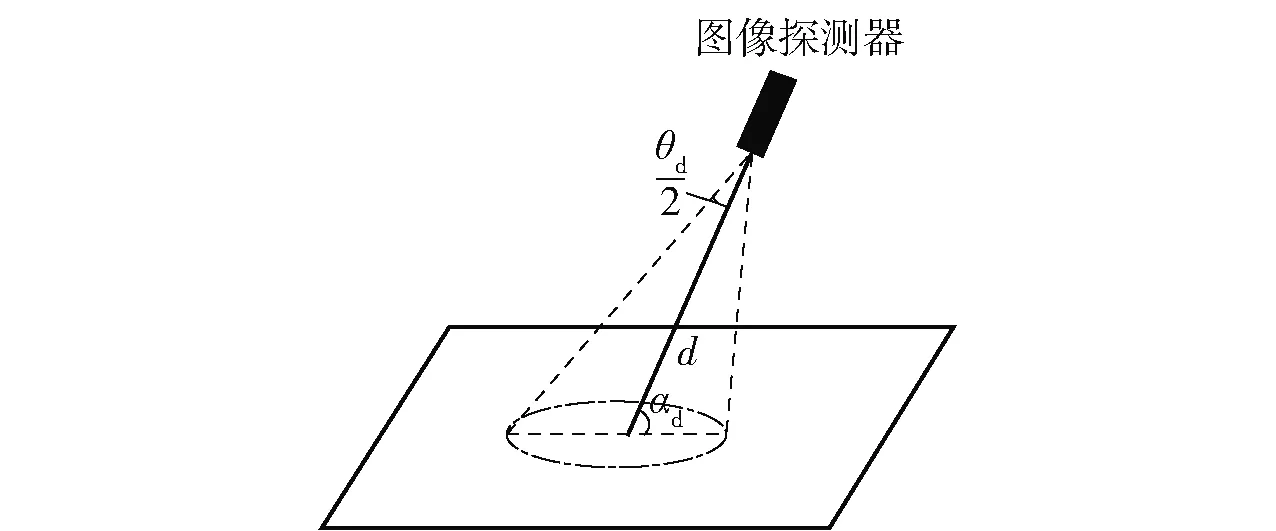
图2 图像探测器探测面积模型

图2中：d代表探测器到目标之间的距离；θd为探测器探测角度(为常量)；αd为图像探测器中线与地面夹角。为保证图像清晰度，通常αd远大于θd/2，将探测区域投影到地面，有效区域等效为圆形，其直径为

(5)

因此探测面积为

(6)

针对图像传感器而言，传感器性能指数λ通过图像传感器探测面积和分辨率共同决定。当探测面积s超过有效信息区域sj时，探测面积越大，则有效区域所占的比重越低，λ越小；当探测面积未超过有效信息区域时，探测面积越大，所占有效区域比重越高，λ越大。

(7)

协同探测系统对目标有效信息的信息熵增益作为系统的评价标准，有效信息的信息熵通过有效图像信息收益和收益信息权重共同描述[9]。在系统工作的tf时间区间内获得的信息熵增益D表示为

(8)

式中：i为探测器编号，i=1，2，3，…，f；ΔRij(t)为编号i的探测器对编号j目标的收益增量。弹载图像探测器通过合理分配修正时机与观测目标，使得系统工作阶段可获取的信息熵最大，图像探测器在切换目标后，收益函数中的初始信息量为切换之前系统对该目标所获取的信息总量，并假设目标在完成修正并稳定后具备目标信息获取能力，如图3所示，图像探测器可针对不同目标进行探测。

图3 目标分配及协同探测

3 图像探测器探测能力评价准则

3.1 二分图模型及标准Kuhn-Munkres算法

通过控制图像子探测器修正时间与观测目标，实现信息熵最大化，本质上是求解多变量的优化问题，本系统中涉及到多个探测器与多个目标之间的多边关系，可采用代数图[10]描述。图是由一组对象以及对象之间的关系构成的图形，其中每个对象可看作图的一个节点，对象之间的关系可看作图的边，由节点和边构成的图记为G(V,E)，其中：V表示节点构成的集合，V={1,2,…,u}，u为节点个数；E表示节点g、h的边构成的集合[11]，E={(g,h)∶g,h∈V}。多探测器观测多个目标，可将系统定义为二分图模型。

定义1若顶点集分成两个非空子集Xn和Yn，并且每条边都有一个顶点在Xn中，另一个顶点在Yn中，则称此图为二分图，模型如图4所示。

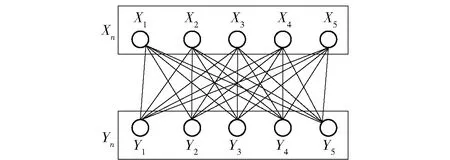
图4 不同观测方式构成的二分图

定义2设具有二分类(Xn，Yn)的赋值二分图G，其中两个顶点分别为Xn={X1,X2,…,Xu}，Yn={Y1,Y2,…,Yu}，任意边Xg、Yh赋权ωgh=ω(Xg，Yh)，设L为G的顶点集V到实数集R的映射，若对任意X∈Xn，Y∈Yn，均有L(X)+L(Y)≥ω(X，Y)，则L为G的可行顶点标记；令EL={XY|e=XY∈E(G)，L(X)+L(Y)=ω(e)}，e为顶点X、Y的映射边，则称EL为边集的二分图G的生成子图为G的相等子图[12]。

求得匹配M权值最大可使用Kuhn-Munkres算法求解，设G=(V,E)为赋权二分图，L是其中一个初始可行顶点标记[13]为

(9)

M是图G的相等子图GL的一个匹配，算法步骤见表2.

表2 Kuhn-Munkres算法

3.2 改进Kuhn-Munkres算法

探测器完成修正后其弹道即可完全预测，在时域空间内对多个目标观测收益可完全预测，二分图模型中赋值权重ωij可等效于i探测器对j目标的信息收益量，即

ωij(t)=[1-(1-R0j)e-λijt]Wj，

(10)

式中：R0j为目标j的初始信息量；λij为探测器i对目标j的性能指数。

Kuhn-Munkres算法可解决瞬时最佳观测目标分配问题，由于图像子探测器在修正后弹道确定，因此在全弹道过程中每时刻对目标探测的收益均为常量，可通过Kuhn-Munkres算法对每个采样点的最优分配方案计算并累加，获得全局最优探测方案，算法运算逻辑如图5所示。

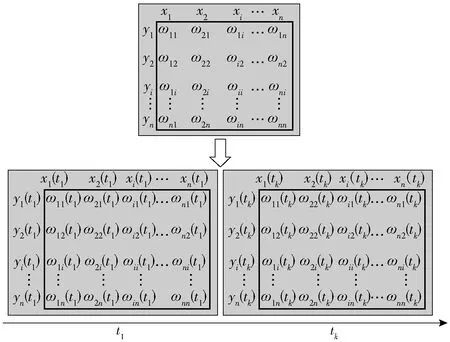
图5 改进Kuhn-Munkres算法模型

在此基础上，探测方案为系统修正时机的函数，即

(11)

式中：τ表示所有子探测器的修正时机；f为探测器个数。针对不同目标，(10)式难以求得解析解，因此考虑数值方法求取最大信息熵增益，将上述问题转化为多元函数在有界闭区间[0，tf]内的最值问题，其中tf为未修正情况下的图像子探测器理论飞行时间，采用Runge-Kutta求解图像子探测器的最优修正时机[14]。改进的Kuhn-Munkres协同探测算法步骤如表3所示。

表3 改进Kuhn-Munkres算法

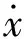
3.3 图像探测器协同算法仿真分析

假设当前战场有3个已知固定目标和3个图像探测器，分别为{x1,x2,x3}以及{y1,y2,y3}，初始数据如表4和表5所示。

表4 目标位置信息

利用表5中的数据带入(2)式中，利用Runge-Kutta算法可以解算出探测器的速度函数v(t)以及姿态函数P(t)，如图6所示。

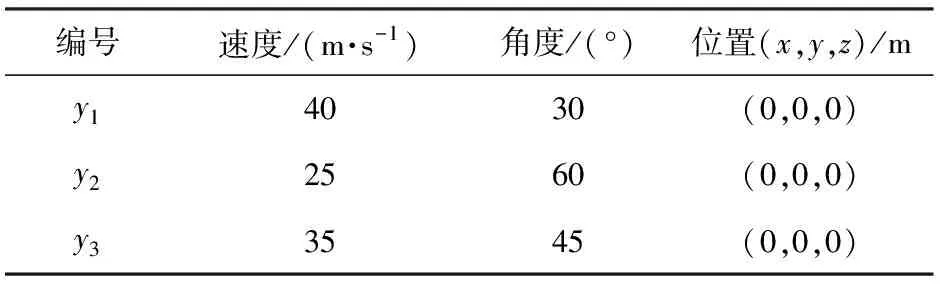
表5 图像探测器初始数据

图6 探测器运动参数

根据弹道参数回带(2)式中，计算出探测器位置函数x(t)和y(t)，如图7所示。

图7 探测器飞行轨迹以及目标位置

联立表4中的目标位置信息、表5中的图像探测器初始数据、速度函数v(t)、姿态函数P(t)和位置函数x(t)、y(t)，利用改进Kuhn-Munkres算法，实现传感器的最优目标分配，结果如图8所示。

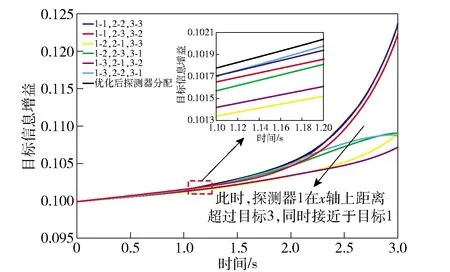
图8 不同探测器分配方式的目标信息增益

图8图例中：1-1，前一位数字代表目标编号1，后一位数字为图像探测器编号1；其他数字组合，以此类推。从图8中可以看出，当图像探测器越过检测目标时，改进的Kuhn-Munkres算法可以及时调整探测器的分配方式，目标信息熵增益同比增长24%。

由于战场环境错综复杂，弹载图像探测器在双方体系对抗中极有可能被摧毁，为了模拟战场环境，验证算法可靠性，做如下仿真实验，设定图像探测器2在1.7 s后被摧毁，结果如图9所示。

图9 探测器运动参数

计算出探测器的位置函数x(t)和y(t)，实现最优分配如图10、图11所示。

图10 探测器飞行轨迹及目标位置

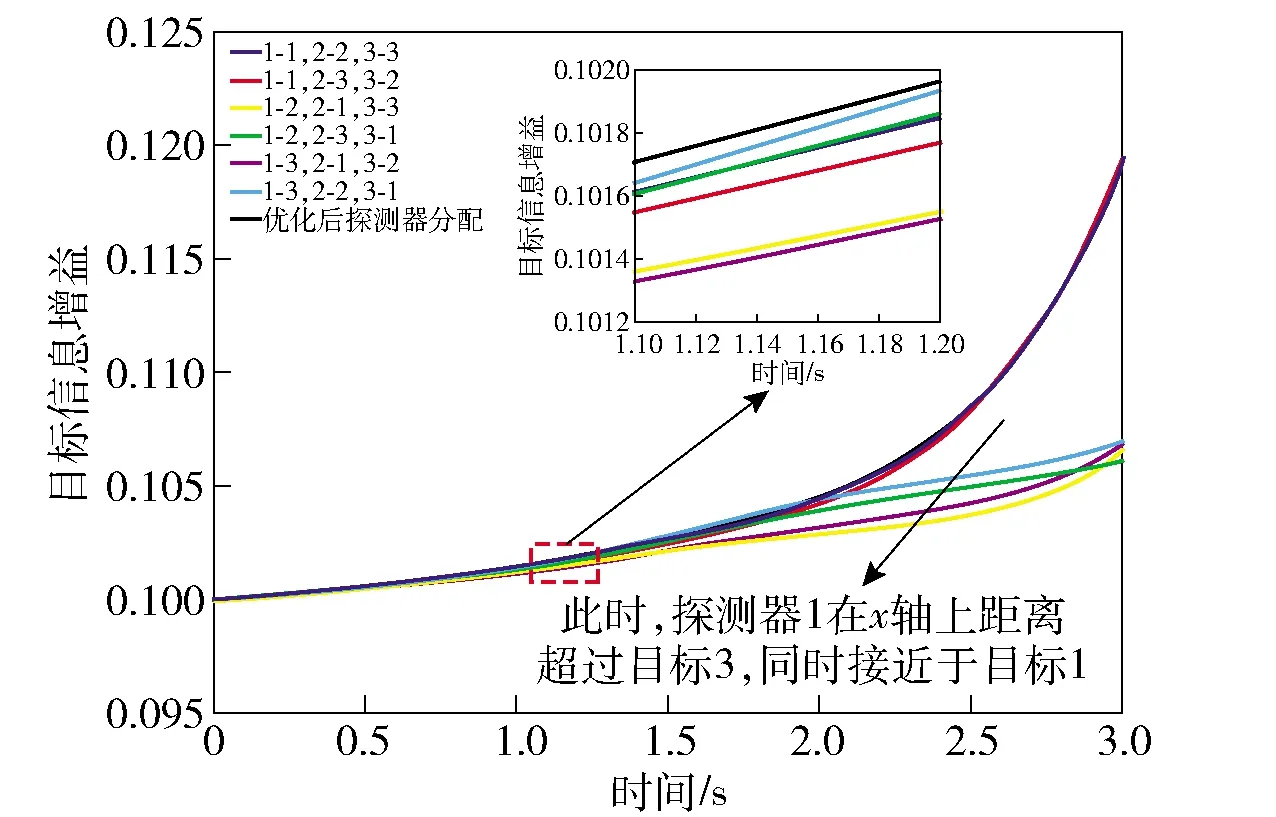
图11 不同探测器分配方式的目标信息增益

即使弹载图像探测器在飞行过程中被摧毁，改进的Kuhn-Munkres算法仍能够有效实现目标分配，实现目标信息增益最大化。

4 结论

本文从毁伤评估系统中弹载图像探测器对集群面目标的探测出发开展研究，针对图像探测器广域协同探测问题，建立了图像探测器的动力学模型，将系统可控变量定义为探测器观测目标分配方法，用集群图像探测器获取的总体信息熵为评价标准。以典型战场事件为例，得出如下主要结论：

1)针对图像探测器对集群面目标的广域协同探测问题，综合Kuhn-Munkres算法和Runge-kutta算法，提出一种改进的Kuhn-Munkres算法，获取最多有效毁伤信息。

2)在图像探测器与目标数量一致和不一致的条件下，实现了弹载图像探测器协同控制，解决了图像探测器协同探测的最优分配问题。

3)改进的Kuhn-Munkres算法有效解决集群图像感知系统对多目标感知中的最优控制策略问题，实现目标信息增益最大化。

本文未考虑更加复杂的战场环境因素问题，其最佳控制策略还有待未来进一步研究。

参考文献(References)

[1] 马春茂,孙卫平,李炎,等.武器装备毁伤评估研究进展[J].火炮发射与控制学报,2019,40(4):96-101.

MA C M,SUN W P,LI Y,et al.Research progress on damage assessment of weapons and equipment[J].Journal of Gun Launch & Control, 2019,40(4):96-101.(in Chinese)

[2] 方有培,汪立萍, 赵霜.信息侦察弹的国外发展及其设计构想[J].航天电子对抗, 2004(4):13-15,19.

FANG Y P,WANG L P,ZHAO S.Foreign development and design conception of information reconnaissance projectile[J].Aerospace Electronic Warfare, 2004(4):13-15,19.(in Chinese)

[3] 李从利,薛松,陆文骏,等.弹载侦察图像质量评价方法研究[J].兵工学报,2017,38(1):64-72.

LI C L,XUE S,LU W J,et al.Research on evaluation method of missile-borne reconnaissance image quality[J].Acta Armamentarii, 2017,38(1):64-72.(in Chinese)

[4] 王正平,刘莉,朱勇.炮射侦察弹炮射减速段弹道优化设计[J].弹道学报,2012,24(4):22-26.

WANG Z P,LIU L,ZHU Y.Optimal design of artillery-launched reconnaissance projectile’s artillery shooting deceleration phase[J].Journal of Ballistics, 2012,24(4):22-26.(in Chinese)

[5] 李卉,邱志明,王航宇,等.电视侦察弹与舰炮武器系统的优化匹配分析[J].兵工学报,2008,29(12):1462-1466.

LI H,QIU Z M,WANG H Y,et al.Optimal matching analysis of TV reconnaissance projectile and naval gun weapon system[J].Acta Armamentarii, 2008, 29(12): 1462-1466.(in Chinese)

[6] 向庭立，王红军,史英春.区域覆盖的多机协同探测任务分配策略[J].空军工程大学学报(自然科学版),2019,20(6):33-38.

XIANG T L,WANG H J,SHI Y C.Multi-aircraft cooperative detection task allocation strategy based on area coverage[J].Journal of Air Force Engineering University(Natural Science Edition), 2019,20(6):33-38.(in Chinese)

[7] 钱杏芳，林瑞雄，赵亚男.导弹飞行力学[M].北京：北京理工大学出版社，2000.

QIAN X F,LIN R X,ZHAO Y N.Missile flight mechanics[M].Beijing: Beijing Institute of Technology Press, 2000.(in Chinese)

[8] 陈俊.一维弹道修正弹修正机构及控制算法研究[D].南京：南京理工大学, 2013.

CHEN J.Research on correction mechanism and control algorithm of one-dimensional trajectory correction projectile[D].Nanjing: Nanjing University of Science and Technology, 2013.(in Chinese)

[9] PEI Y E, LI L I, XIAO Z, et al.Dynamic spectrum allocation based on Kuhn-Munkres algorithm to guarantee cognitive users’ QoS[J].Journal of Shanghai Normal University(Natural ences), 2013, 42(2):137-142.

[10] 王树禾.图论及其算法[M].合肥：中国科学技术大学出版社, 1990.

WANG S H.Graph theory and its algorithm[M].Hefei:University of Science and Technology of China Press, 1990.(in Chinese)

[11] TEMELSO B, MABEY J M, KUBOTA T, et al.ArbAlign: a tool for optimal alignment of arbitrarily ordered isomers using the Kuhn-Munkres algorithm[J].Journal of Chemical Information and Modeling, 2017, 57(5):1045.

[12] FRANCOIS B, LASSALLE J C.An extension of the Munkres algorithm for the assignment problem to rectangular matrices[J].Communications of the ACM，1971, 14(12):802-804.

[13] ZHU H B, ZHOU M C, ALKINS R.Group role assignment via a Kuhn-Munkres algorithm-based solution[J].IEEE Transactions on Systems, Man, and Cybernetics-Part A: Systems and Humans, 2012, 42(3):739-750.

[14] PAMELA M.B, KEVIN B.Structure-preserving Runge-Kutta methods for stochastic Hamiltonian equations with additive noise[J].Numerical Algorithms.2014, 65(3):519-532.

[15] DANG Q A, MANH T H.Positive and elementary stable explicit nonstandard Runge-Kutta methods for a class of autonomous dynamical systems[J].International Journal of Computer Mathematics, 2020, 97(10):2036-2054.