基于MATLAB的六轴机械臂运动学分析与验证

蔚芳鑫,孙明革,周海宇

(吉林化工学院 信息与控制工程学院，吉林 吉林 132022)

如今工业生产各领域都对机器人的控制精度提出了更高的要求，而机器人的运动学分析是机器人控制技术的重要理论基础，也是进行轨迹规划的前提，分析并建立正确的运动学模型是研究机器人问题中必不可少的重要先行环节[1-2].采用MATLAB作为运动学仿真验证平台，是目前广为使用的一种方法，利用其中的Robotics Toolbox机器人工具箱可以很好地完成对机器人运动学模型的仿真与验证，通过建模可以得到三维可视化的机器人本体模型，也可以很直观地看到机器人的运行效果[3-4].因此对Hyundai-Hs220型六自由度机械臂开展研究，建立理论正逆运动学模型，基于MATLAB平台及Robotics Toolbox进一步检验运动学模型的正确性与合理性.

1 机器人模型建立与运动学分析

1.1 建立运动学模型

本研究以韩国现代公司生产的Hyundai-HS220工业机器人为载体，它是典型的六自由度工业机器人[5-6]，较一般的机器人来说，其特点是负载能力较强，达220 kg.图1(a)为机械臂实物图.基于六自由度工业机器人运动特性的复杂度以及相关结构参数较多，为清晰、直观地表达机器人各关节的关系和位姿，采用改进的D-H建模方法建立如图1(b)所示的机器人各关节的坐标系[7]，建立步骤如下：

(1)确定原点

在相邻两关节轴i-1和i间的公垂线与i-1轴的交点或两轴交点处确定为原点.

(2)定出Zi-1轴及其方向

以关节轴i-1作为Zi-1轴，且其方向指向该关节轴.

(3)定出Xi-1轴及其方向

关节轴i和i-1间的公垂线方向即为Xi-1轴的方向

(5)依照右手定则确定Xi-1轴.

(a)

依据图1(b) 所建立的坐标系并按照D-H约定的规则推定出各连杆参数值并建立如表1所示的D-H参数表，表中i表示关节序号，θi为关节角度，di为两邻近关节偏移的距离，ai-1为邻近两关节连杆的长度，αi-1为关节扭转角.

表1 Hyundai-HS220型机器人D-H参数表

1.2 正运动学分析

正运动学分析过程，就是将机器人各连杆当作自变量，研究机器人末端执行机构的位姿相对于机器人基坐标系之间的变换关系，并推导出正运动学方程[8-9].依据齐次坐标变换的方法及D-H参数表，可以得到如式(1)所示求解相邻关节间坐标变换矩阵的一般表达式：

(1)

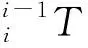
(2)

其中：

nx=c1[c23(c4c5c6-s4s6)-s23s5s6]+s1(s4c5c6+c4s6) ；

ny=s1[c23(c4c5c6-s4s6)-s23s5s6]-c1(s4c5c6+c4s6) ；

nz=-s23(c4c5c6-s4s6)-c23s5c6，

ox=[s23s5s6-c23(c4c5c6+s4c6)]c1-(s4c5s6-c4c6)s1；

oy=[s23s5s6-c23(c4c5c6+s4c6)]s1+(s4c5s6-c4c6)c1；

oz=s23(c4c5c6+s4c6)+c23s5s6；

ax=c1(c23c4c5-s23c5)-s1s4s5；

ay=s1(c23c4c5-s23c5)+c1s4s5；

az=s23c4s5-c23c5；

px=c1(a3c23-d4s23+a1+a2c2) ；

py=s1(a3c23-d4s23+a1+a2c2) ；

pz=-d4c23-a3s23-a2s2.

(3)

以上求解出的各表达式即构成了正运动学方程，若设置一组关节角度θ1～θ6，则通过上述方程的计算，就能得到机器人末端的位姿.

1.3 逆运动学分析

θ1=Atan2(py,px)或θ1=Atan2(-py,-px) ，

(4)

(5)

θ3=Atan2(a3n-d4m,a3m+d4n) ，

(6)

θ6=Atan2(m2s3+n1c3,m1s3-n2c3)或θ6=Atan2[-(m2s3+n1c3),-(m1s3-n2c3)] ，

(7)

θ5=Atan2[ayc1-axs1,(nyc1-nxs1)c6+(oxs1-oyc1)s6] ，

(8)

θ4=Atan2(s4，c4) ，

(9)

2 运动学仿真验证

为了验证所推导的正逆运动学方程的正确性，采用MATLAB Robotics Toolbox机器人工具箱进行运动学模型的建立，它能够提供多种运动学函数来支持建模[10].依据表1的D-H参数并通过调用相关函数编写程序完成建模.给定一组关节角度theta=[000000],得到如图2所示机器人的初始位姿模型.

图2 机器人模型

2.1 正运动学仿真

正运动学方程的仿真，主要是通过给定一组关节角度，用推导的正运动学方程和机器人工具箱的fkine运动学函数来分别进行末端位姿矩阵的计算，若结果一致则说明所建立的正运动学模型正确.由于手动计算较为复杂，所以将正运动学方程的推导过程在MATLAB中编写成函数脚本.首先给出一组关节角度theta=[0-pi/3pi/3000],由正运动学函数进行验证结果如下：

由Robotics Toolbox机器人工具箱验证结果如下：

通过数据对比发现，所建立的正运动学方程是正确的.

2.2 逆运动学仿真

逆运动学仿真，是通过工具箱算出位姿矩阵，由逆解方程运算得到机器人到达该位姿各关节所需的角度，并将该组角度作为输入，由工具箱中的正解函数fkine来进行验证，若解出的位姿矩阵与给定矩阵一致，则逆运动学方程建立正确.现给出用工具箱fkine函数算出的位姿矩阵：

同于正解仿真过程，将逆解推导流程通过MATLAB编写成函数脚本，运行程序并将得到的关节角度回代到工具箱中得到：

二者结果相同，验证了逆运动学方程的正确性.

3 轨迹规划仿真

轨迹规划基本方法主要归为关节空间和笛卡尔空间轨迹规划两种，无论选用哪种方法最终都要满足轨迹的平滑连续[11].关节空间轨迹规划由于其是以关节角变量的函数来规划轨迹的，可以直观并实时地看到各关节角的变化情况，不存在机构奇异性.所以本文选用关节空间轨迹规划方法来进行规划.随机设置空间中两点，即初始位姿点和终止位姿点，设定到达初始位姿点所需的关节转角为qs=[0 0 0 0 0 0]，到达终止位姿点所需的关节转角为qf=[pi/3,-pi/3,pi/6,-pi/6,-pi/7,-pi/4] ，调用机器人工具箱函数jtraj，其格式为：

[qqdqdd]=jtraj[qs,qf,t].

(10)

运行程序得到了如图3所示6个关节的角度位移、角速度及角加速度变化曲线.

t/s(a)关节角位移

对图3进行观察并分析得知，所有关节的角位移、角速度、角加速曲线均连续且平滑，机器人能够平稳地从初始位姿运动到终止位姿，各关节没有出现异位突变现象，没有产生较大的震荡，满足规划需求.

4 结 论

基于MATLAB的机器人工具箱平台，对所建立的运动学方程进行了验证，并完成了在关节空间的轨迹规划，得到了各关节运动参数的轨迹变化曲线.结果表明机器人运行效果良好，可以平稳地从初始位姿运动到终止位姿，所建立的运动学模型可以作为后续研究的理论支撑.