半潜式平台自由衰减时域运动数值仿真
祝 港,刘培林,黄福祥,田立锋,昝英飞,黄 阔
(1.哈尔滨工程大学 船舶与海洋工程学院,黑龙江 哈尔滨 150001;2.海洋石油工程股份有限公司,天津 300461)
0 引 言
近年来,海洋油气资源的勘探开发成为各国的重要战略目标,半潜式平台(简称“平台”)由于甲板面积大、环境适应力强、可移动性高等优点成为海洋油气开采的首选装备[1]。数值仿真已成功应用于海洋石油开采过程,海上作业平台运动学数值模型的准确性研究是海上作业数值仿真的重要环节。由于平台的自由衰减运动响应能较准确地反映平台的阻尼系数、固有周期等重要参数[2-3],横摇、纵摇和垂荡的自由衰减运动响应与平台自身结构有关,因此研究平台的自由衰减运动响应对校核其运动学数值模型有重大意义[4-6]。WANG等[7]通过CFD仿真研究平台纵摇自由衰减运动,根据自由衰减曲线计算阻尼系数与衰减周期,研究结果表明,在有系泊状况下自由衰减固有周期的仿真结果与模型试验结果基本一致,纵摇运动幅值在前半周期完全吻合,系泊装置会影响衰减阻尼,随着时间增加平台运动峰值差异逐渐增大。刘鲲[8]测量平台在微小幅度下六自由度衰减曲线,并采用频域方法获取结构固有周期和阻尼系数,与数值计算结果进行对比,研究结果表明:在纵荡、横荡自由衰减时刚度主要由锚泊系统提供,与模型试验结果相比误差较大;在横摇、纵摇、垂荡自由衰减时刚度由结构自身提供,较为准确。因此,可选取横摇、纵摇、垂荡等3个自由度进行研究。
本文以陵水17-2平台为研究对象,建立运动学数值仿真模型,完成平台横摇、纵摇、垂荡等3个自由度的自由衰减数值仿真,将数值仿真结果与模型试验结果进行对比,以验证仿真模型的准确性。
1 仿真模型搭建
1.1 时域运动模型
从平台运动学和动力学模型出发,根据牛顿第二定律,建立平台时域运动分析方程:
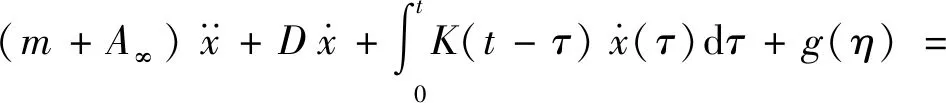
(1)
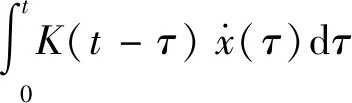
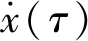
(2)
式中:Ar、Br、Cr分别为状态方程的3个常系数矩阵;xr为状态向量矩阵。
时域运动模型须满足稳定性、无源性,以及辨识方法便用性[10]。
1.2 阻尼系数获取
(3)
式中:Nθ为阻尼系数。
平台由横摇角θi变化至θi+1的势能ΔE为
(4)
式中:mp为平台质量;h为平台初稳心高。
横摇阻尼消耗能量W为
(5)
由式(4)与式(5)相等得:
(6)
式中:wθ为平台固有频率;θm=(θi+θi+1)/2,为相邻幅值的平均值。
θm与差值Δθ=θi-θi+1成线性关系,即
Δθ=aθm
(7)
式中:a为消灭系数。a与Nθ的关系为
(8)
无因次化后,无因次阻尼系数uθ为
(9)
自由衰减相邻振幅绝对值比值的减幅系数为η,阻尼比ξ可通过η进行求解:
(10)
式中:Ai为第i个振幅。
2 时域运动分析
2.1 目标平台参数
研究对象为陵水17-2平台,可用于1 500 m深水油气开采,是具有万吨储油能力的半潜式生产平台[12]。其由1座方形平台甲板、4根方形立柱和4个浮筒构成,具体参数如表1所示。
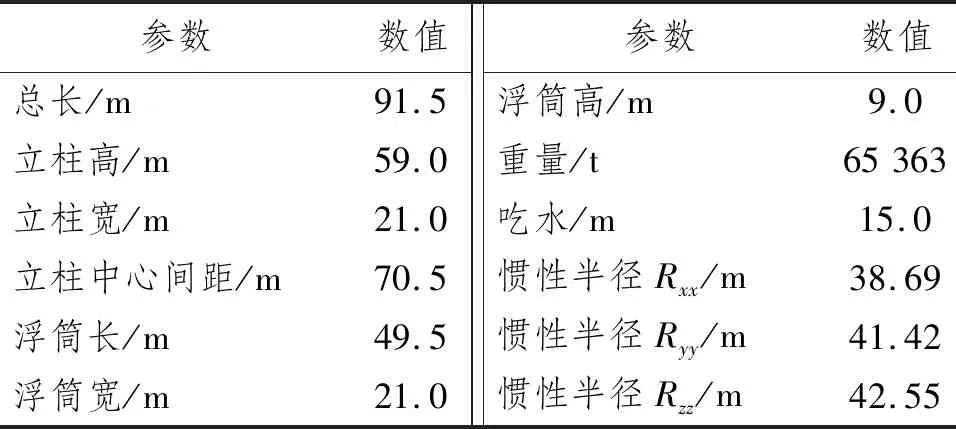
表1 陵水17-2平台参数
2.2 水动力模型
通过Sesam软件建立平台三维面元模型,分别设定网格密度为2.0 m、1.5 m、1.0 m,研究网格密度对深水平台附加质量和阻尼的影响,具体计算结果分别如图1和图2所示。
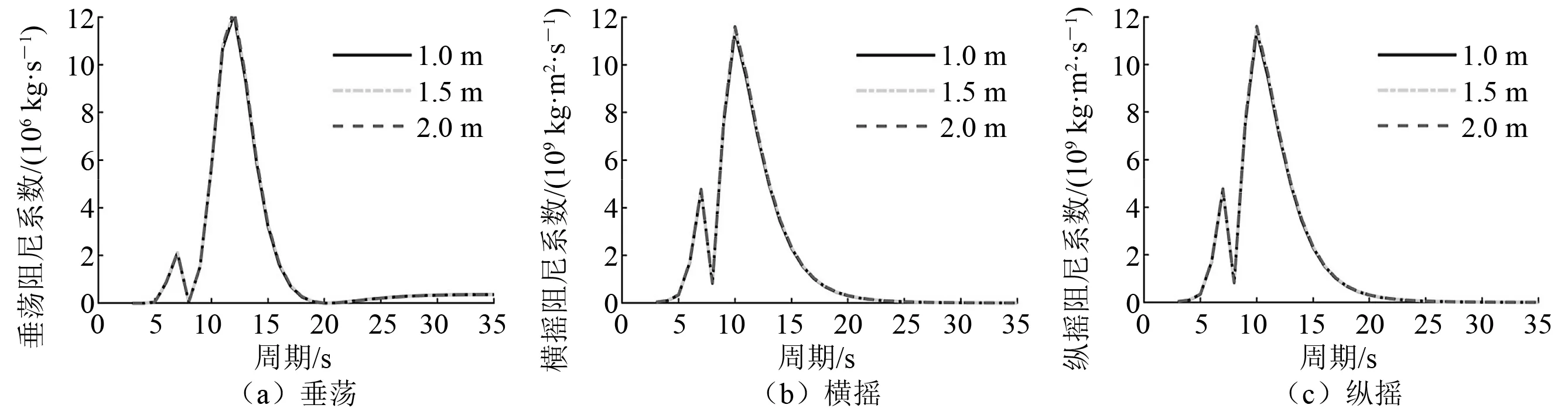
图2 平台不同网格密度的阻尼结果对比
由图1可知,平台附加质量曲线在不同网格密度下的趋势基本相同,网格密度越小,曲线振荡幅度越小,计算结果越精确。考虑到软件的网格数限制和计算效率要求,模型网格密度不能划分过细。当网格密度划分为1.0 m时,计算结果已满足精度要求。
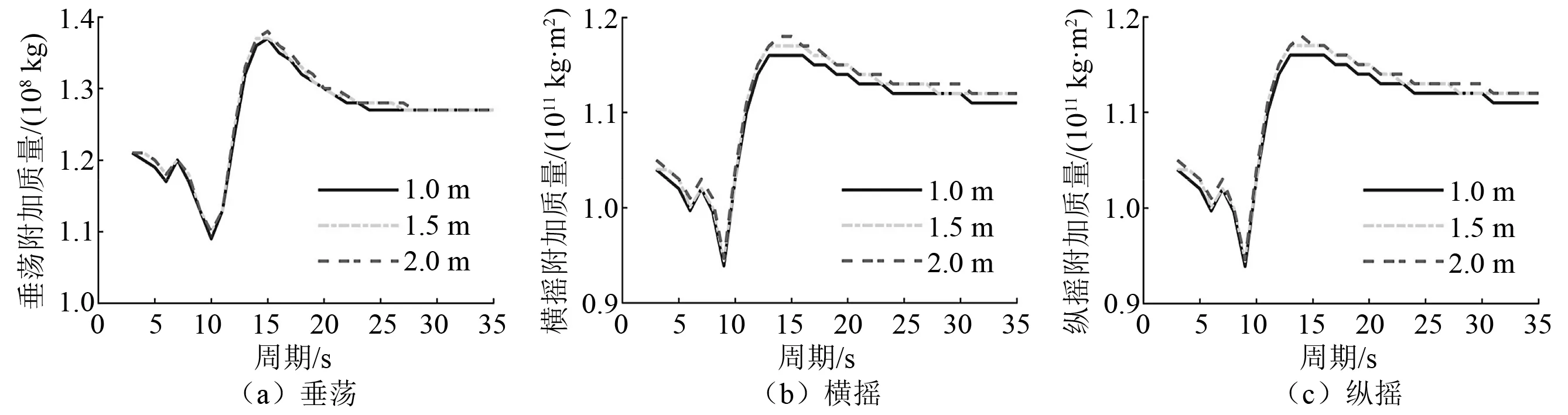
图1 平台不同网格密度的附加质量结果对比
由图2可知,平台在3种网格密度下的六自由度阻尼系数曲线几乎重合,证明模型在当前网格密度下的计算结果已足够精确,不用再细分。
结合平台不同网格密度的附加质量结果,选取1.0 m为单位划分网格。平台面元模型如图3所示。

图3 平台面元模型
2.3 仿真结果分析
模型试验在静水条件下进行,由于在平台运动过程中重力效应起主导作用,因此缩尺模型试验选取的基本理论是Froude相似准则,即保证平台模型与实物的Froude数相等:
(11)
(12)
式中:vp、Lp、Tp分别为平台实物的速度、长度和周期;vm、Lm、Tm分别为平台模型的速度、长度和周期;g为重力加速度。本模型试验缩尺比为60,海水与淡水密度比为1.025,水池最深位置达40 m。平台模型自由衰减初始值如表2所示。

表2 平台初始偏移量
平台垂荡、横摇、纵摇自由衰减运动响应结果对比如图4所示。
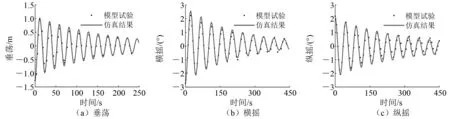
图4 平台自由衰减曲线对比结果
由图4可知,平台垂荡方向的自由衰减基本与模型试验结果一致,横摇、纵摇方向的自由衰减在前3个周期内拟合较好,在第4个周期往后出现一定程度的误差,但基本趋势一致。误差产生原因可能是在模型试验过程中平台横摇、纵摇方向的自由衰减产生的波浪对横摇、纵摇本身造成影响。在2个周期内,模型试验与仿真结果的周期与阻尼比如表3所示。
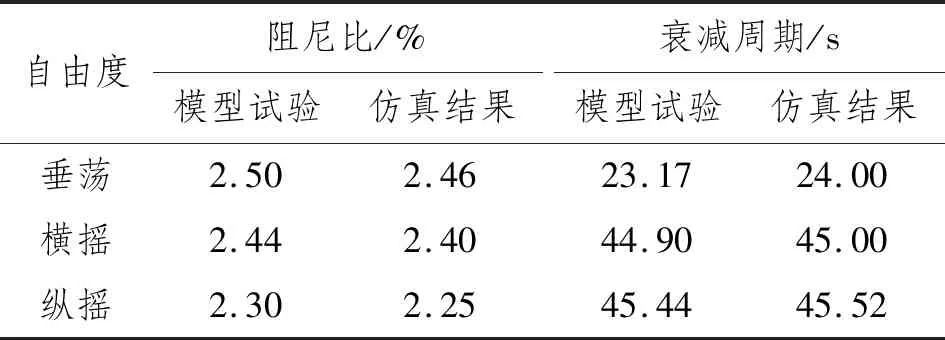
表3 自由衰减结果对比
由表3可知:在前2个周期内模型试验与仿真结果的垂荡衰减阻尼比误差为1.60%,横摇衰减阻尼比误差为1.60%,纵摇衰减阻尼比误差为2.20%,阻尼比误差均小于5.00%;在前2个周期内仿真结果与模型试验的垂荡衰减周期误差为3.50%,横摇衰减周期误差为0.22%,纵摇衰减周期误差为0.17%,衰减周期误差同样均小于5.00%。证明数值仿真结果与模型试验结果基本一致。
横摇和纵摇消灭曲线如图5所示。
由图5可知:根据平台横摇数据点拟合得到横摇消灭曲线函数为y=0.197 9x-0.013 24,横摇消灭系数为0.197 9,横摇无因次阻尼系数uθx为0.063;纵摇消灭曲线函数为y=0.143 2x+0.018 97,纵摇消灭系数为0.143 2,纵摇无因次阻尼系数uθy为0.046。
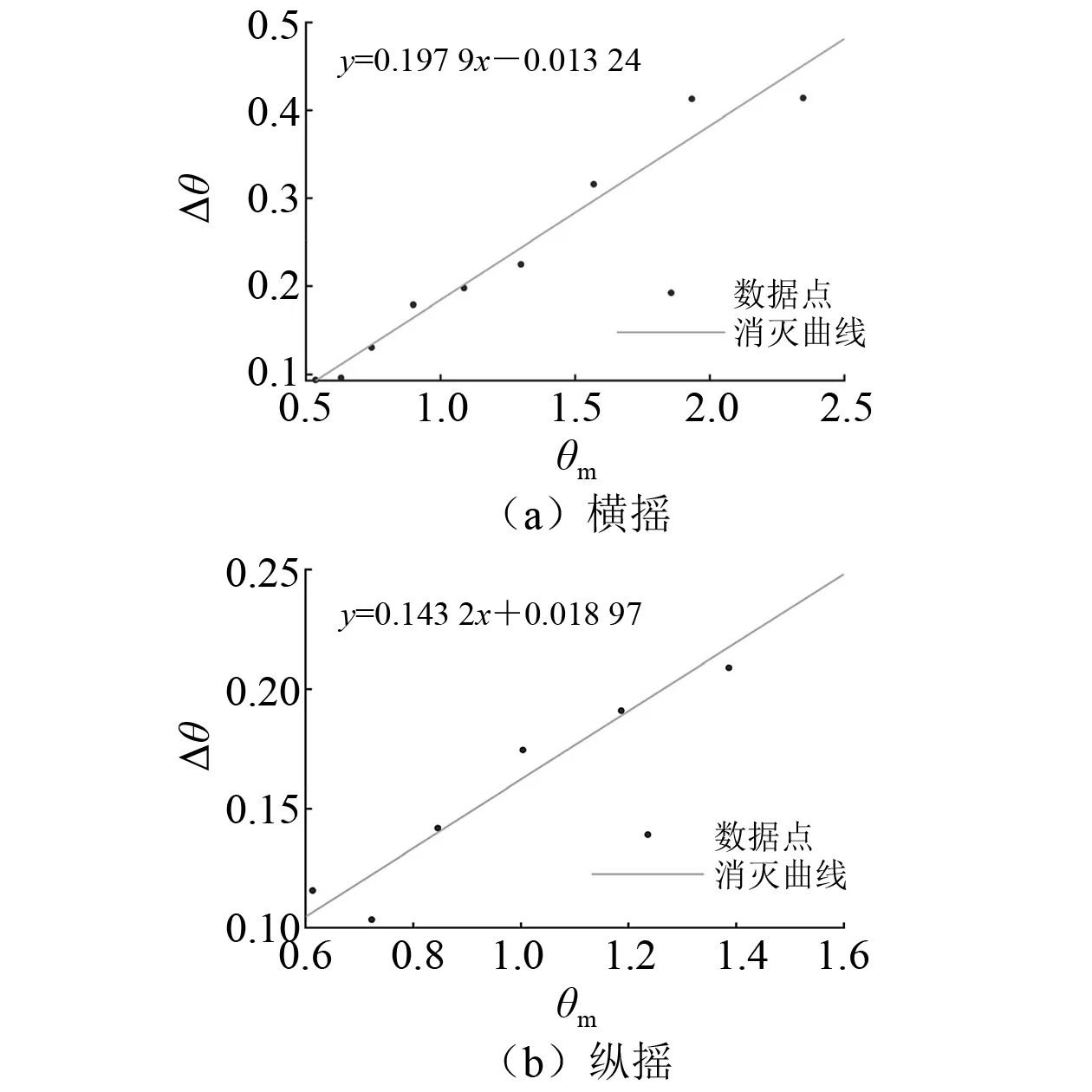
图5 横摇纵摇消灭曲线
平台自由衰减阻尼力(矩)时历曲线如图6所示。平台在自由衰减过程中阻尼力(矩)呈衰减状态,其衰减周期与自由衰减运动周期一致,衰减幅值呈二次曲线。在垂荡自由衰减过程中最大阻尼力为1.58×105N,在横摇自由衰减过程中最大阻尼力矩为1.7×106N·m,在纵摇自由衰减过程中最大阻尼力矩为106N·m。在衰减过程中阻尼力(矩)大小与平台的速度有关。由于阻尼力(矩)的存在,平台所能到达的速度幅值逐渐减小,阻尼力(矩)随之逐渐减小,平台衰减也逐渐减慢。
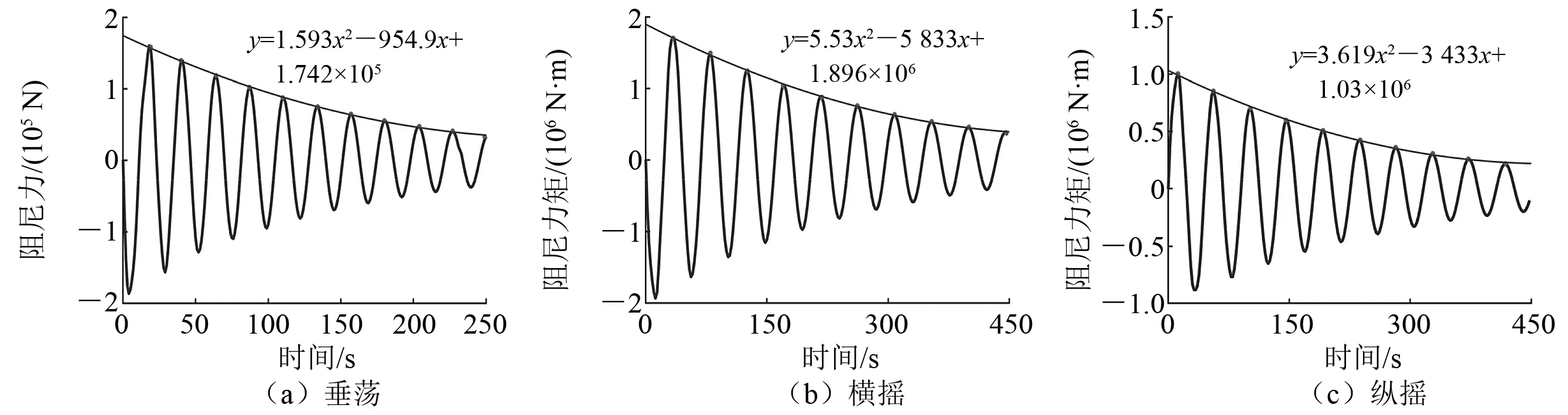
图6 平台自由衰减阻尼力(矩)时历曲线
3 结 论
搭建陵水17-2平台运动学仿真模型,并分析不同网格密度对平台六自由度附加质量和阻尼系数的影响,选取合适网格划分模型单元,针对平台的自由衰减运动开展数值仿真研究,并通过模型试验对仿真结果进行校核。具体结果如下:
平台自由衰减运动衰减仿真结果与模型试验结果基本一致,仿真结果的阻尼比和衰减周期与模型试验结果相比误差均在5%以内。根据自由衰减曲线得到横摇、纵摇消灭曲线,计算自由衰减线性阻尼系数。分析平台在自由衰减过程中阻尼力(矩)时历变化曲线,发现平台在衰减过程中阻尼力(矩)与平台的运动速度有关,在整个自由衰减过程中阻尼力(矩)幅值衰减呈二次曲线形态,与平台运动幅值衰减形态基本一致。研究结果表明,所搭建的陵水17-2平台运动学仿真模型具有一定的准确性,可用于开展其海上作业平台运动评估。

