FPSO典型舱段极限强度
谷家扬,冯湖川,渠基顺,李成军,李 荣,万家平
(1.江苏科技大学 a.海洋装备研究院;b.船舶与海洋工程学院,江苏 镇江 212003;2.中国船舶及海洋工程研究院,上海 200011;3.南通中远海运船务工程有限公司,江苏 南通 226001)
0 引 言
浮式生产储卸油装置(Floating Production Storage and Offloading,FPSO)作为海上油气开发的主力装备一直是国际海洋工程界的研究热点。以荷兰SBM Offshore公司为代表开发的通用型FPSO可在通用主结构上适配各种接口以满足更广泛海域的要求,批量生产主船体可缩短建造周期以提高经济性。因此,有必要对FPSO主船体的舱段结构进行极限强度分析以确定其承载能力与设计冗余度。
彭大炜等[1]归纳分析弧长法、阻尼因子法与准静态法在求解结构极限承载力中的计算特点与求解思路,通过结果对比验证准静态法在计算较大模型时具有较大优势。张水林[2]采用载荷/结构响应一体化分析系统研究某阿芙拉型远洋油船在规则波中不同浪向角作用下的船体梁极限强度,计算得到的极限强度较船体方法得到的极限强度偏小。林瞳等[3]采用Abaqus准静态分析法对纵剪和纵扭联合作用下的半潜平台进行研究,详细探讨加载点位置、网格尺寸和不同纵剪纵扭载荷比对计算结果的影响。王崇磊[4]、昝森[5]、袁梦等[6]研究超大型集装箱船在三向载荷联合作用下的极限强度及其相互影响模式,并提出表征集装箱船三维极限强度安全区域的公式。王醍等[7]利用非线性有限元法分别计算基于单跨梁与舱段模型的船体梁极限强度,并探讨上层建筑对极限承载力的影响。石宝雨[8]利用Smith简化计算法和非线性有限元法对破损船体的剩余极限强度进行计算分析,发现船舶破损后的不同浮态对极限承载能力有较大影响。
LEE等[9]参考船舶实际结构建立非等厚加筋板模型,采用有限元分析法与迭代增量法对模型极限抗压强度进行分析,为计算变厚度板的极限抗压强度的结构建模提供指导。TANAKA等[10]采用一系列薄壁梁单元对船体梁模型进行简化并采用Smith法计算截面在弯扭组合作用下的极限抗弯强度,将该简化方法应用于组合荷载作用下的缩尺模型连续破坏试验,对比试验和有限元结果,讨论简化方法的有效性。LEE等[11]研究3种不同尺寸集装箱船船体结构在垂向弯曲及扭转组合作用下的极限强度,采用ALPS/HULL3D程序计算船体结构的渐进崩溃行为,在此基础上给出船体梁极限强度与垂向弯矩和扭矩的关系。LIU等[12]采用LS-DYNA求解器对某集装箱船船体结构在单调和中拱中垂循环弯矩作用下的极限强度进行计算与对比,发现在循环荷载作用下由于塑性应变累积和塑性破坏交替发生,船体梁极限强度较单调弯矩作用时偏弱。
本文结合研究对象作业海域的波浪载荷情况,应用Abaqus准静态非线性有限元法研究舱段结构在垂向载荷与水平载荷联合作用下的极限强度及结构破坏失效模式。对比不同的弯矩转角曲线以确定适用于本模型的载荷加载速率,由整船波浪直接计算得到的弯矩传递函数比值确定联合载荷工况下中垂与水平载荷加载比例关系,比以往采用一系列载荷比例的计算方式更进一步。
1 FPSO舱段模型介绍
以荷兰SBM公司设计的深水通用FPSO为研究对象,该FPSO能满足墨西哥湾、巴西、西非等多个作业海域的工作要求,主尺度如表1所示。

表1 FPSO主尺度 m
结合各船级社规范对极限强度校核模型范围的要求且考虑到本FPSO的实际结构形式,建立1/2+1+1+1/2肋距(三档强框)有限元模型,如图1所示。按照相关规范要求,模型采用的网格尺寸为1/6纵骨间距。FPSO货舱区域纵向骨材皆由尺寸较大的T形板组成。为更真实地模拟货舱区域在极限状态下的受力情况,T形板腹板及尺寸较大的扁钢采用4节点或3节点壳单元模拟,T形板面板及尺寸较小的加强筋采用梁单元模拟。一般而言,船体梁的极限强度由纵向结构决定,横向构件并不直接承载外力,但由文献[13]可知横向构件会参与模型弯矩转角曲线的卸载段,且横向构件的缺失可能会导致纵向构件提前出现屈曲失效。为保证计算结果与实际情况更接近,所建立的3档强框模型包括强框架等横向结构。

图1 FPSO舱段3档强框有限元模型
初始缺陷及焊接残余应力对极限强度有一定的影响,但变形量大小的确定及加载方式较复杂,为重点关注结构在联合载荷下的极限强度响应,暂不考虑初始缺陷的影响。FPSO货舱区域结构由AH36、AH32、Q235等3种不同钢材组成,在计算时一般将材料假定为理想弹塑性,主要材料参数如表2所示。
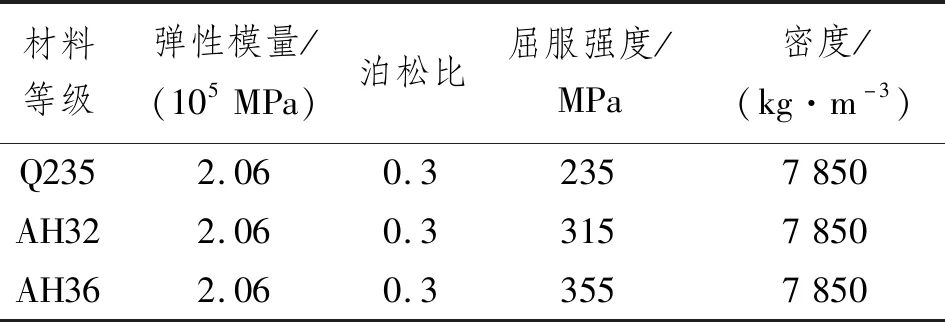
表2 模型材料主要参数
2 舱段结构在垂向载荷下的极限强度
2.1 加载速率对计算结果的影响
Abaqus/Explicit显式动力学分析需要准确追踪结构在短时间作用载荷下的应力响应,不同的载荷加载速率会导致结构响应的差异。因此,有必要对模型的加载速率进行探讨,选取模型转角加载速率分别为0.001 0 rad/s、0.002 0 rad/s和0.000 5 rad/s。以中垂计算工况为例,不同转角加载速率下弯矩-转角关系如图2和表3所示。
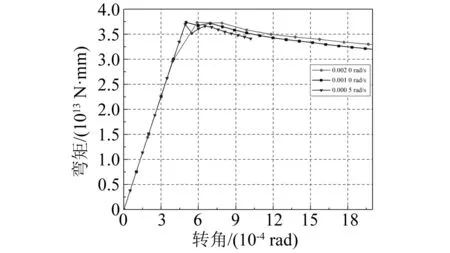
图2 转角加载速率对中垂计算结果的影响
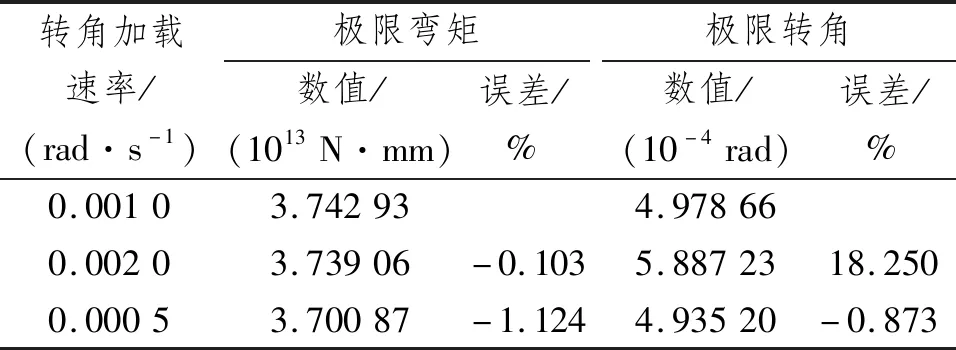
表3 不同转角加载速率下极限弯矩与转角对比
由图2和表3可知,3种转角加载速率下的极限弯矩相差并不大,误差都在2%以内,在转角加载速率为0.000 5 rad/s下捕捉到的极限弯矩最小。当转角加载速率为0.002 0 rad/s时,虽然极限弯矩相差不大,但在到达极限状态前出现2段斜率不同的曲线,不符合材料的线性特点。转角加载速率为0.001 0 rad/s与0.000 5 rad/s的计算区别主要体现在载荷曲线的卸载阶段。在此阶段舱段更多发生的是非纵向构件的变形等破坏,较慢加载速率对应的曲线走势变化较大,可进一步确定载荷卸载阶段的外力传递路径。且由于0.000 5 rad/s加载速率较慢,在线性变化阶段即结构达到极限弯矩前的数据更丰富,便于对结构开展后续分析。因此,最终选取的加载速率以0.000 5 rad/s为准。
2.2 垂向载荷作用下舱段结构极限强度
在中拱与中垂载荷作用下,舱段结构对极限强度的承载表现出不同的特点,对应的弯矩-转角曲线如图3所示。
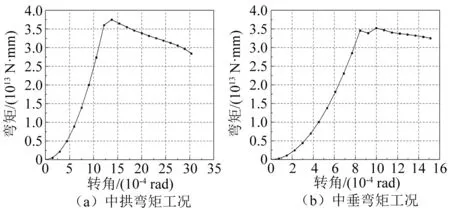
图3 中拱中垂载荷弯矩-转角曲线
在载荷加载初始阶段,曲线表现出非线性即刚度不一致的现象,这是由于模型采用3种不同屈服强度的钢材,结构处于初步确定传导路径的阶段。在后续的加载时刻曲线基本保持线性变化的特点。
中拱和中垂对应的极限弯矩分别为3.756×1013N·mm和3.525×1013N·mm,满足一般船型的极限强度规律即中拱极限承载能力强于中垂工况。极限状态时的结构应力分布如图4所示。在极限时刻受到压缩载荷的甲板与船底板中部发生明显的屈曲破坏且破坏区域贯穿整个船宽方向。在中拱极限时,整个舭部与甲板结构达到材料应力屈服点,但由AH36钢材构成的舷侧外板结构应力远未达到材料屈服应力。中垂极限弯矩发生时的破坏形式稍有不同,由弯矩-转角曲线可知极限承载力经历了先下降后上升至极值的阶段。对比极限弯矩前一时刻,此时甲板中部虽发生大面积破坏但并未左右贯穿,舷侧外板起到类似于甲板纵骨的作用且支撑效果更好,有效阻止了屈曲破坏的传导,但其自身结构在一定区域内也达到屈服极限。在中垂弯矩达到极值时,不仅整个甲板中部发生屈曲失效而且失效区域沿纵舱壁与内壳板向型深方向传导,内壳板破坏范围更大,向下延展至第3层平台板,舷侧外板的破坏区域也较前一时刻更大。
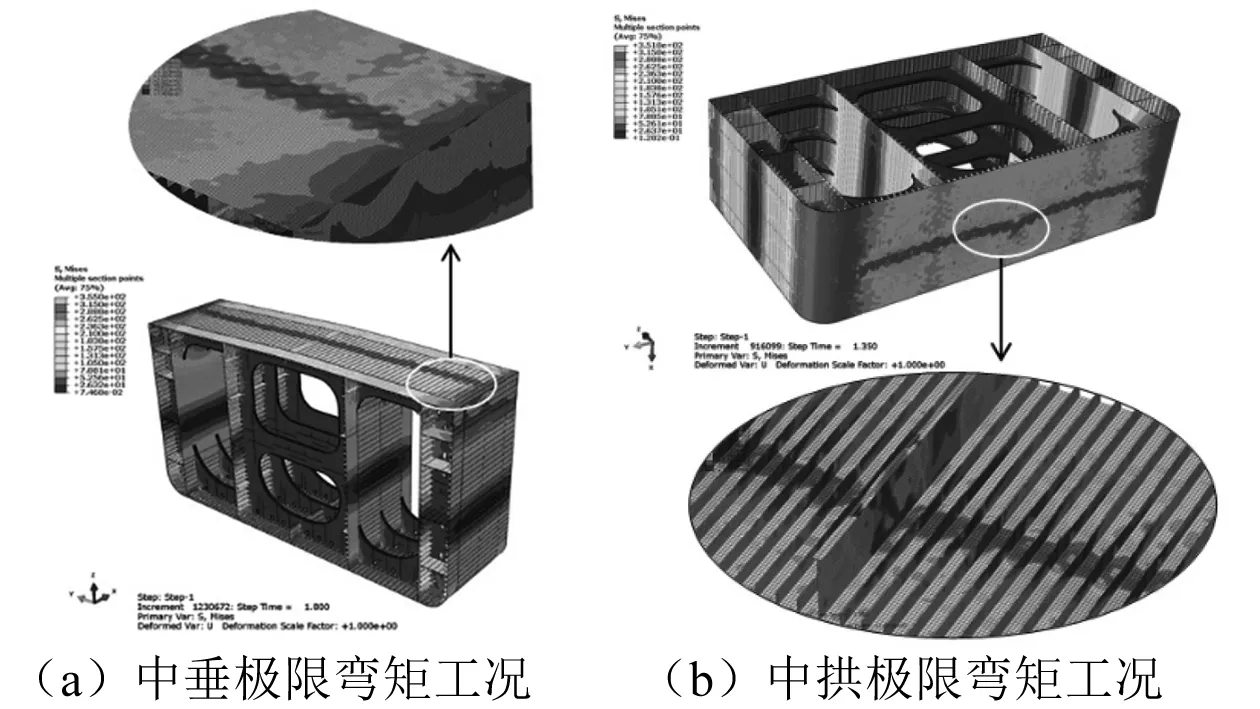
图4 中拱中垂极限弯矩时结构应力分布云图
3 舱段结构在联合载荷下的极限强度
3.1 联合载荷加载速率比例确定
目标FPSO主要承受垂向弯矩载荷,FPSO转塔系统产生的风标效应会降低结构受到水平弯矩作用的概率与角度,但在一定海况下仍存在水平弯矩与垂向弯矩联合作用于船体结构的情况。结合FPSO适用作业海域的海况,假定水平弯矩与船首夹角最大值为30°。为进行联合弯矩下极限强度研究,需要先确立模型在2个方向上的转角加载速率。采用FPSO整船在30°斜浪下的垂向与水平方向弯矩幅值响应算子(Response Amplitude Operator,RAO)比值作为加载速率之间的比例关系,计算得到的结果如图5和图6所示,图5和图6中站位与FPSO沿船长方向位置的关系如表4所示。
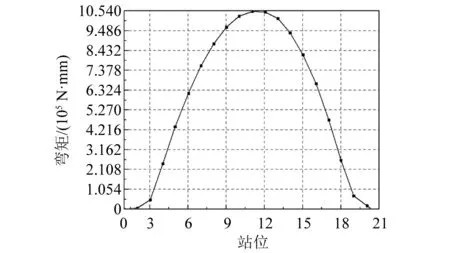
图5 30°艏斜浪下垂向波浪弯矩RAO值
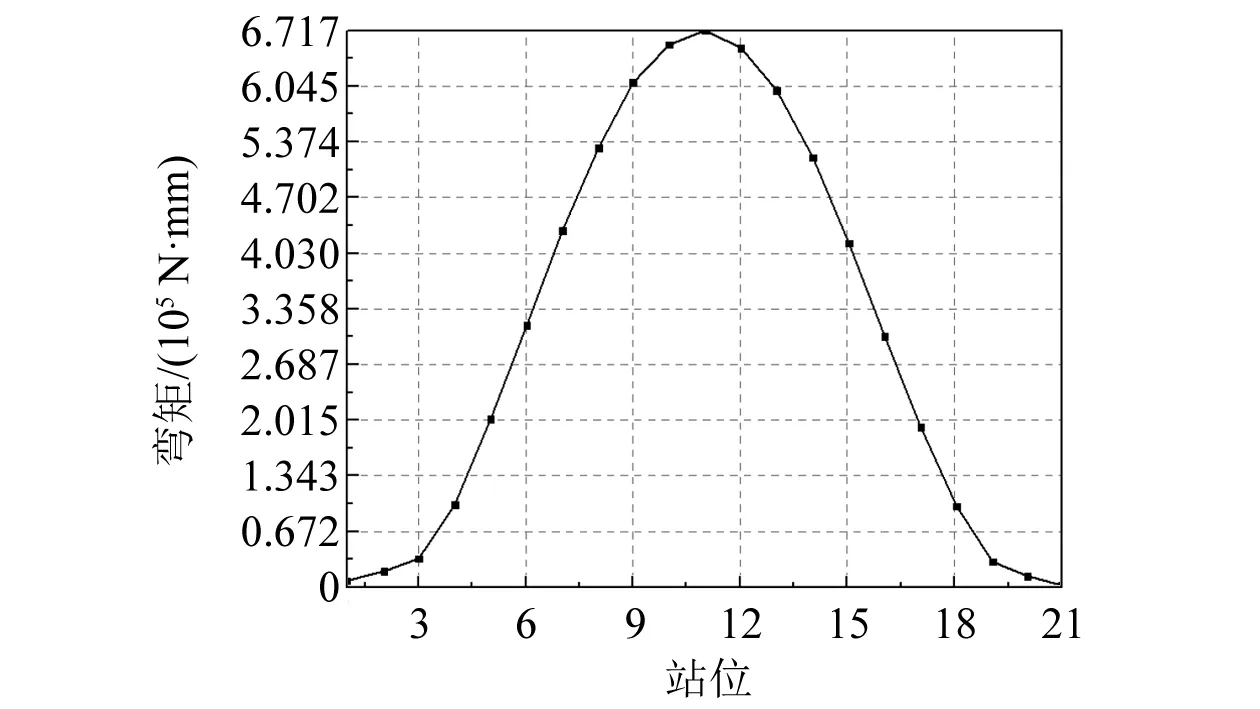
图6 30°艏斜浪下水平波浪弯矩RAO值
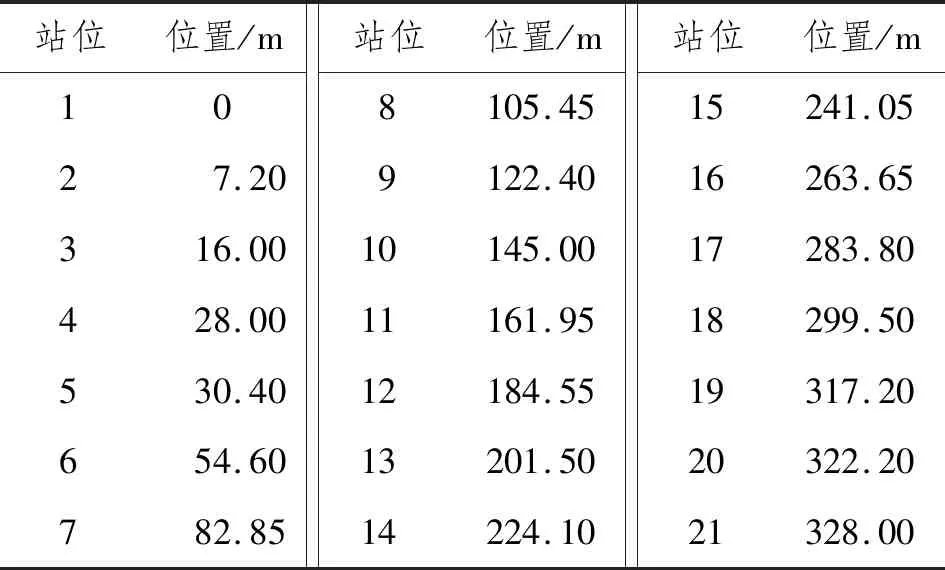
表4 站位沿船长方向位置关系
由图5和图6可知,在30°艏斜浪时,垂向波浪弯矩RAO为10.540×105N·mm,水平方向波浪弯矩RAO为0.672×105N·mm。由于此时波浪载荷预报为同一波高,可直接将两者RAO比值作为30°艏斜浪下船体受到的垂向波浪弯矩与水平波浪弯矩之比,约1.5∶1.0。计入静水垂向弯矩后的垂向弯矩与水平弯矩比值约3∶1。因此,模型最后确立的垂向弯矩与水平弯矩转角加载速率为3∶1,具体加载速率比为0.001 2 rad/s∶0.000 4 rad/s。
3.2 联合载荷极限强度
在计算时长为3 s时得到的模型在中垂/中拱与水平联合载荷作用下的弯矩-转角曲线如图7和图8所示。在2种计算工况下水平极限弯矩均比垂向极限弯矩提前出现,在中垂联合工况下两者出现时刻间隔较大(分别为1.05 s和1.80 s),在中拱联合工况下两者出现时刻接近(分别为1.05 s和1.50 s),这是由舷侧外板与甲板/船底板相比较小的纵向面积导致水平承载力较弱所决定的。中垂联合工况的弯矩-转角曲线在卸载阶段变化幅度较中拱联合工况小,这说明FPSO甲板与船底板对联合载荷的承载方式有较大不同。
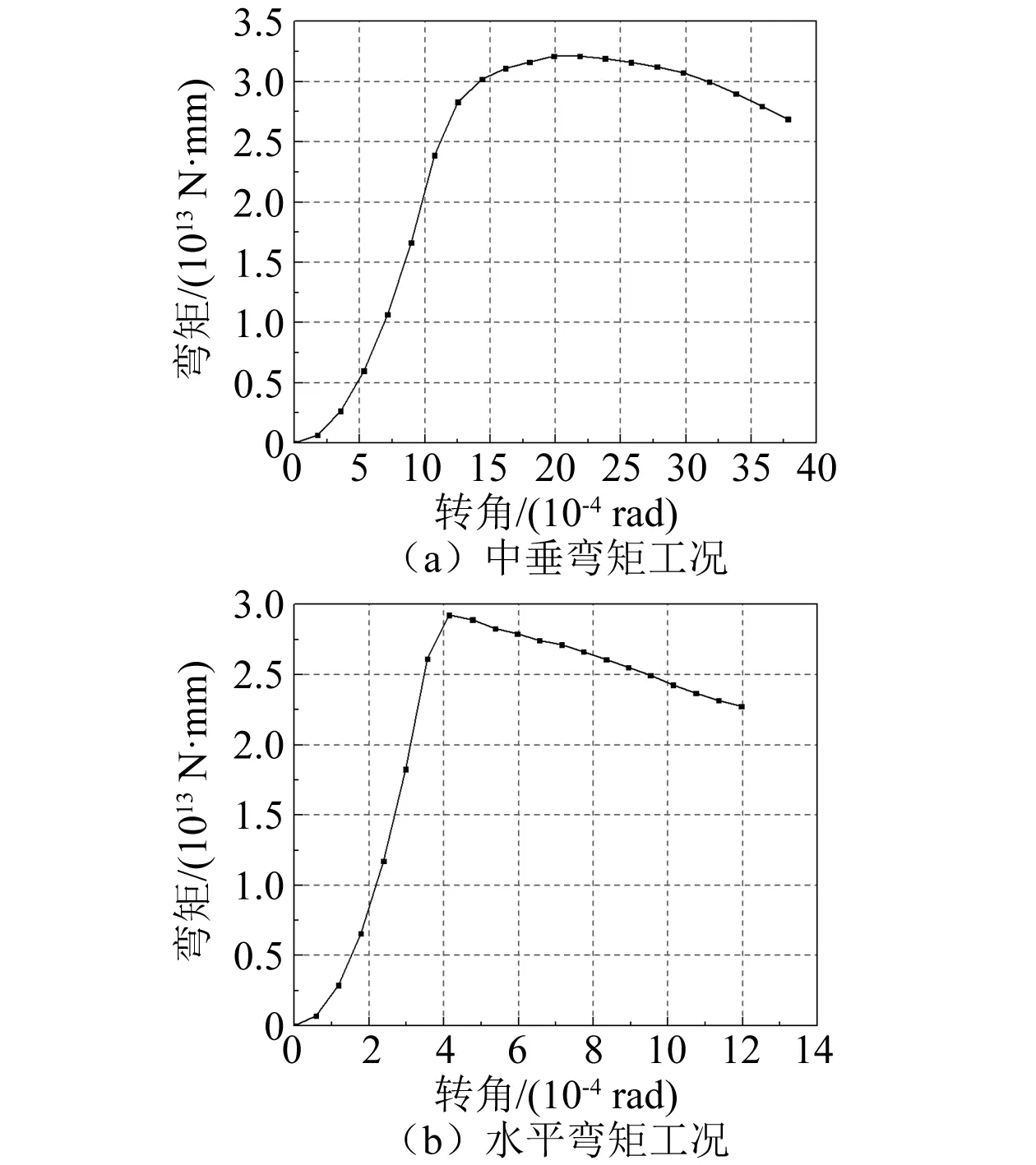
图7 中垂联合载荷弯矩-转角曲线
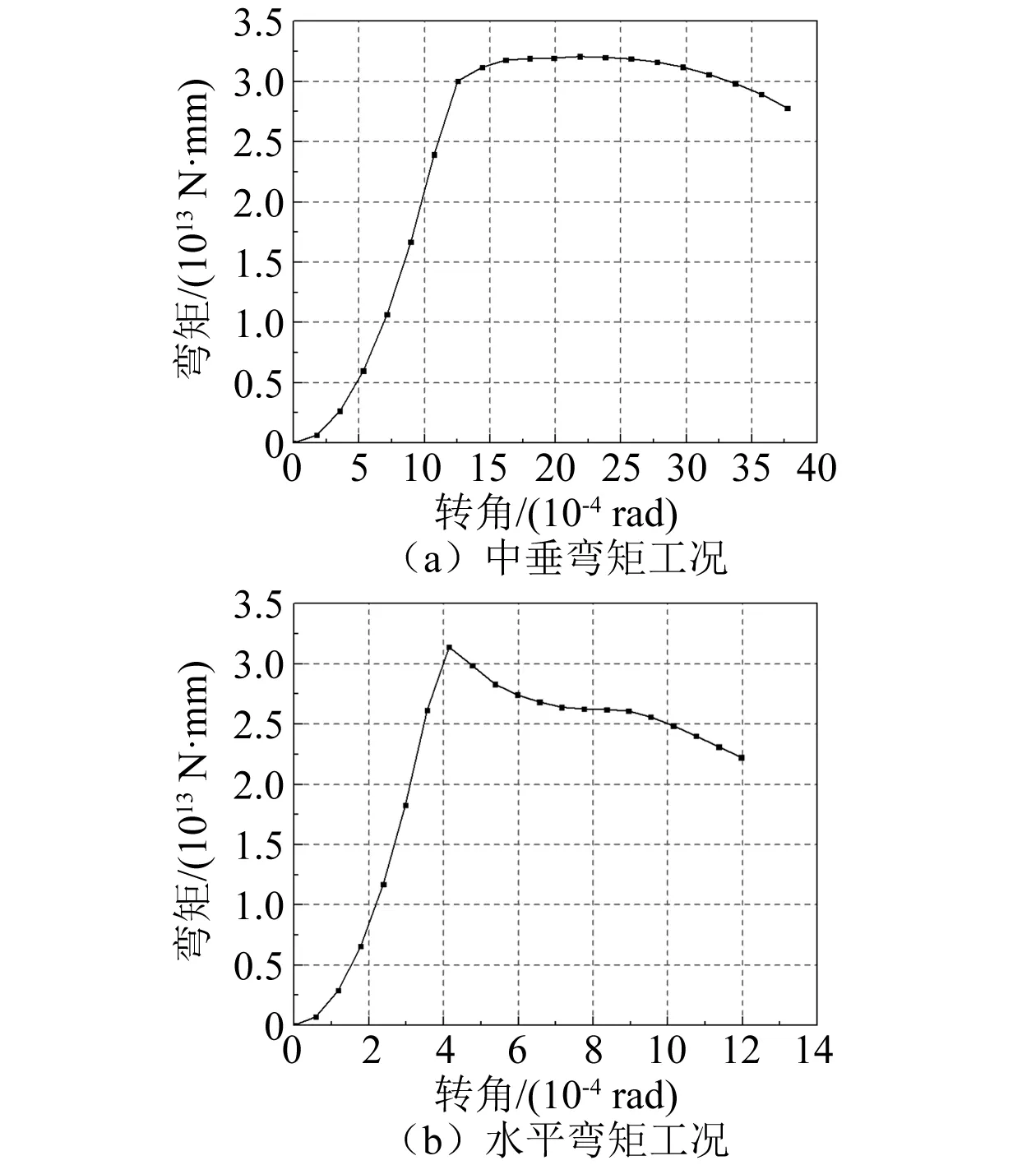
图8 中拱联合载荷弯矩-转角曲线
舱段结构在各方向上达到极限弯矩时的相应应力云图如图9~图11所示,在水平弯矩与垂向弯矩联合作用下整个模型的应力分布呈现反对称的受力特点,即在中垂联合弯矩作用下左上区域受压、右下角受拉,在中拱联合弯矩作用下结构右上侧受拉、左下角受压。在中垂联合工况下,水平弯矩先达到极值并使左舷侧外板失去水平承载能力,此时左舷侧受压发生贯穿式屈曲破坏且屈曲变形区域向甲板大面积延伸但未连通左右两舷。当甲板结构屈曲破坏区域左右贯通时,垂向极限弯矩也随之出现。此时水平载荷也在继续增加,由于舷侧外板失去抵抗能力,载荷传递至附近的平台板与内舷侧板并使其发生局部屈曲变形。在中拱联合弯矩作用下由于舭部结构的存在较好地承载了联合载荷,在水平极限弯矩发生时舷侧并未发生屈曲破坏,仅左舷外板与舭列板连接区域部分网格达到材料屈服极限。随着转角的增加及前期的应力累积,船底板与左舷外板结构发生从连接处向右向上扩展的屈曲破坏,但在达到垂向极限弯矩时船底板与舷侧板屈曲失效区域并未两边贯通。

图9 中垂联合工况水平极限弯矩时应力分布云图
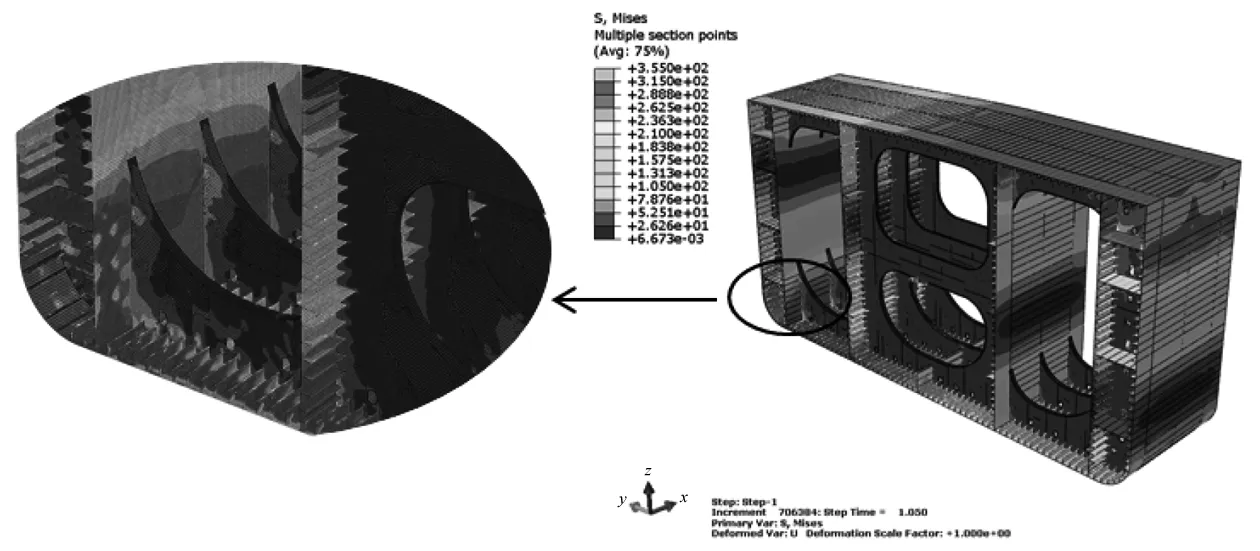
图10 中拱联合工况水平极限弯矩时应力分布云图
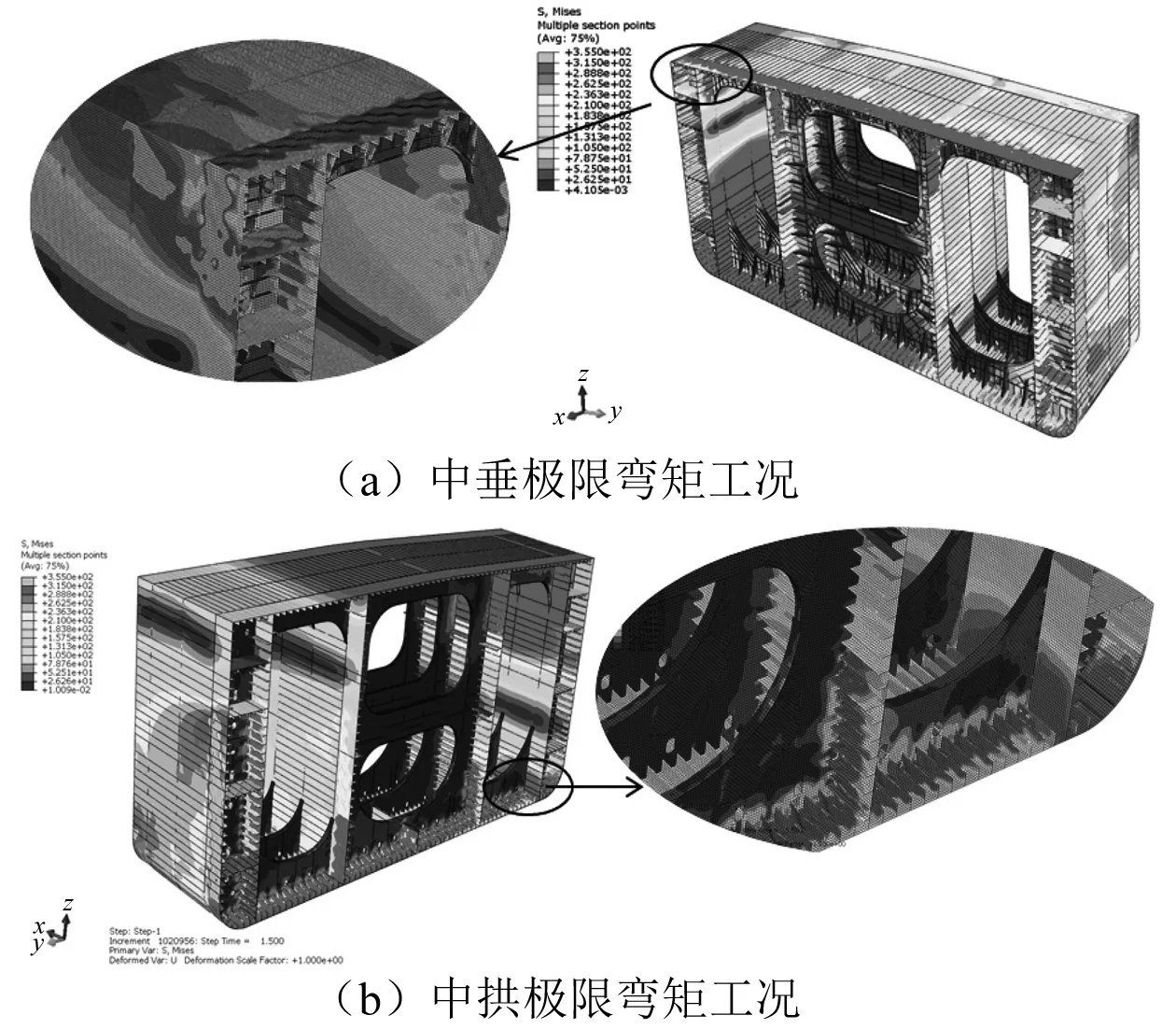
图11 中垂中拱极限弯矩时应力分布云图
将联合工况与单一方向上的极限弯矩进行对比,统计结果如表5所示。在单一载荷作用下FPSO舱段结构表现出一般船舶的规律即中拱工况极限强度大于中垂工况,且由于较大的型宽及舷侧结构采用AH36高强钢,水平极限弯矩明显强于垂向极限弯矩。在联合载荷作用下,由于引入另一方向上的变量,载荷均有所下降,其中:在联合工况下中拱和中垂弯矩较对应单向载荷时分别下降8.88%和19.52%,可见水平载荷的存在对中拱极限承载力的影响更大;在联合工况下中垂与中拱水平弯矩降幅接近,分别为52.57%和49.06%。
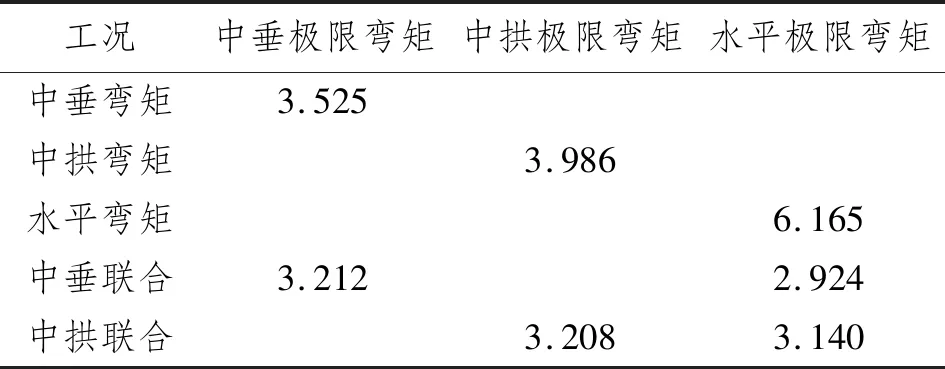
表5 联合工况与纯弯或水平弯矩结果对比 1013 N·mm
4 结 论
采用Abaqus准静态分析法对FPSO舱段结构3档强框模型进行非线性有限元分析,确定适用于本模型的转角加载速率及联合载荷作用时的速率比,得到模型在中拱、中垂和30°艏斜浪时水平弯矩与垂向弯矩联合载荷作用下的极限强度以及对应工况的破坏模式与载荷承载方式,得出以下结论:
(1)FPSO货舱段结构中和轴靠近基线,造成船底板的剖面模数大于甲板,舱段结构在仅受垂向载荷作用时中拱极限弯矩大于中垂极限弯矩,即船底板抵抗垂向载荷的能力强于甲板结构。
(2)在联合载荷作用下水平弯矩的存在使本通用型FPSO舱段结构垂向极限弯矩减小,对中拱极限弯矩影响更甚,使联合载荷作用下的中拱极限弯矩弱于中垂极限弯矩。
(3)中拱联合载荷下的结构响应情况比中垂联合载荷好,舭部结构有效起到了联合载荷的承载与传递功能,表现为水平载荷承载能力达极限时舷侧结构未发生屈曲破坏,且中拱极限弯矩发生时船底板和舷侧板屈曲失效区域并未贯通板架整体结构。

