考虑海上意外时间和合作协议的班轮运输船期设计鲁棒优化

杨华龙，赵帅奇，方旭，段静茹

（大连海事大学，交通运输工程学院，辽宁大连 116026）

0 引言

集装箱班轮运输具有客户多、货物价值高、运输时间性要求强等特征[1]。船公司需要在设定的航线上，以预先公布的船期(船舶到、离港时间)为客户提供稳定的班轮运输服务[2]。然而，由于受恶劣天气和海况等不确定性因素的影响，船长经常需要对各航行区段的航速进行调整，使得船舶实际航速与计划航速发生偏离，产生海上意外时间，导致船期不稳定。因此，考虑海上意外时间的班轮运输船期设计鲁棒(稳健)优化研究具有重要的现实意义。

航速是决定船期的重要因素，NG[3]在假定航速确定的条件下，构建了班轮运输船期设计问题的非线性混合整数规划模型。AYDIN 等[4]研究具有船舶限时到港情况下的航速优化和船期设计问题，建立了非线性规划模型。DULEBENETS[5]进一步基于船舶到港多时间窗、多装卸效率等合作协议，构建了航速和船期设计优化模型。

上述研究均假设船舶海上航行状态是稳定的。然而，海上意外时间造成的船期不稳定会对班轮运输运营组织造成不利的影响。为此，WANG等[6]通过按各航段距离的一定比例设定航段富裕航行时间，以缓冲海上意外时间造成的船期延误，建立了以船舶航次运营成本最小为目标的班轮运输船期，设计混合整数非线性规划模型。但该研究在对船期鲁棒性设计时，未考虑船期方案对港口装卸作业调度以及客户服务水平的影响[7]。

为此，本文针对海上意外时间所造成的船期不稳定问题，在文献[6]研究的基础上，进一步结合港船间合作协议，分析船期变化对港口装卸作业调度以及客户服务水平的影响，建立航速偏离与港口装卸成本、船舶迟到惩罚成本和集装箱货物库存成本的关系，构建班轮运输船期设计非线性混合整数规划鲁棒优化模型，为船公司船期设计决策提供参考。

1 问题描述

在航运供应链整合的背景下，船公司通过与各挂靠港口签署合作协议，可获得多时间窗、多起讫时刻和多装卸效率，某时间窗拥有的多起讫时刻如图1所示。

图1 多起讫时刻Fig.1 Mutiple start/end times

在图1中，某时间窗的3 个开始时刻分别为某日的18:00、次日0:00 和次日6:00，3 个结束时刻分别为第3日0:00、6:00 和12:00。由此可知，该时间窗可衍生出3×3 共9个子时间窗。

在船期设计时，依据港-船合作协议，船公司可以在各航段通过优化船舶航速，选择合适的船舶到港、离港时刻。同时，船公司需要结合各航段船舶海上意外时间经验数据，为各航段设置航行缓冲时间[8]，并在各航段船舶航行时间的细分区间(此区间内船舶航速保持不变)上。为了保证船期设计得到的计划航行时间满足海上意外时间出现于船舶航行在航段任意位置时的到港时间要求，应采用“先快后慢”的非匀速航行策略[1]，确保船舶在航行中有足够时间对冲海上意外时间。因此，本文提出考虑海上意外时间和合作协议下的集装箱班轮运输船期设计优化问题的解决思路为：依据船舶海上意外时间经验数据，设置缓冲时间比例系数，结合船舶驾驶操纵实际，细分各航段船舶航行时间区间，并根据“先快后慢”的航行策略，求解各细分区间优化航速，构建鲁棒性的班轮运输船期设计优化模型，实现班轮运输服务总成本最小的目标。

为便于建模，作以下基本假设：

(1)航线配置的船舶类型一致；

(2)船舶挂靠的港口及顺序已知；

(3)发船频率为周班。

2 模型构建

2.1 参数与变量

(1)集合

Ρ——航线上港口集合，亦为相邻港口间航段集合，Ρ={1,…,N}，N为港口数；

Δp——港口p的时间窗集合，Δp={1,…,Kp} ，Kp为港口p时间窗数，p∈P；

Φpt——港口p时间窗t的开始时刻集合，Φpt={Spt1,Spt2,…,Spts,…,SptKpt} ，Kpt为第p个港口第t个时间窗的开始时刻数量，SptKpt为港口p时间窗t的第Kpt个开始时刻，p∈P，t∈Δp；

Ψpt——港口p时间窗t的结束时刻集合，Ψpt={Ept1,Ept2,…,Epte,…,EptKpt} ，EptKpt为港口p时间窗t的第Kpt个结束时刻，p∈P，t∈Δp；

Ωp——港口p装卸效率集合，Ωp={Hp1,Hp2,…,Hph,…,HpMp} ，Mp为港口p装卸效率数，HpMp为港口p的第Mp个装卸效率，p∈P。

(2)参数

Cves——船舶每周运营成本(美元·周-1)；

Cph——港口p在装卸效率h下的装卸成本(美元·h-1)；

Cinv——集装箱货物的单位库存成本(美元·(TEU·h)-1)；

Cp——船舶在港口p迟到单位惩罚成本(美元· h-1)；

Cfeu——单位燃油成本(美元· t-1)；

Ccan——船舶过运河成本(美元·次-1)；

Lp——航段p的距离(n mile)；

Qp——船舶在航段p上装运集装箱的总量(TEU)；

Rp——船舶在港口p装卸集装箱的总量(TEU)；

Vmax——船舶的最高航速(kn)；

Vmin——船舶的最低航速(kn)；

Γp——船舶在航段p上航行缓冲时间比例系数(h·n mile-1)。

(3)决策变量

tp——船舶在航段p的航行时间(h)；

ap——船舶到达港口p的时刻；

dp——船舶离开港口p的时刻

hp——船舶在港口p的装卸时间(h)；

wp——船舶在港口p的等待时间(h)；

lp——船舶在港口p的迟到时间(h)；

m——航线上配置的船舶数量(艘)；

xpt——当船舶选择时间窗t到达港口p时为1，否则为0；

xpts——当船舶选择在港口p时间窗t第s个开始时刻Spts时为1，否则为0；

xpte——当船舶选择在港口p时间窗t第s个结束时刻Epte时为1，否则为0；

xph——当船舶在港口p选择第h个装卸效率Hph时为1，否则为0。

2.2 航段燃油消耗量最小化模型

设船舶在航段p时刻q的实际航速为vpq，则在航段p时刻q的燃油消耗速度函数g(vpq)[6]为

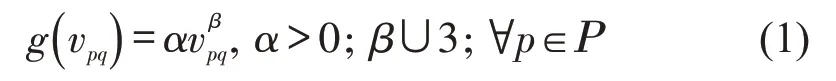
式中：α，β——船舶燃油消耗系数。

于是，在航段p船舶航行时间tp内的燃油消耗量C(tp)为

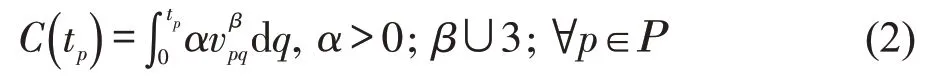
为了应对船舶在航段p的海上意外时间，船公司依据各航段船舶海上意外时间经验数据，预留缓冲时间，并在航段p航行时间tp内采取船舶航速先快后慢的策略。因此，需要确定船舶在航段p上使燃油消耗量最小的最佳航行速度v*pq，故有航段燃油消耗量最小化模型M1。

目标函数为

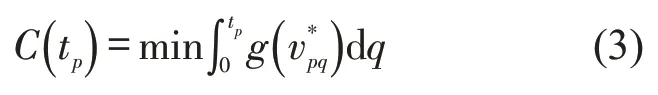
约束条件为

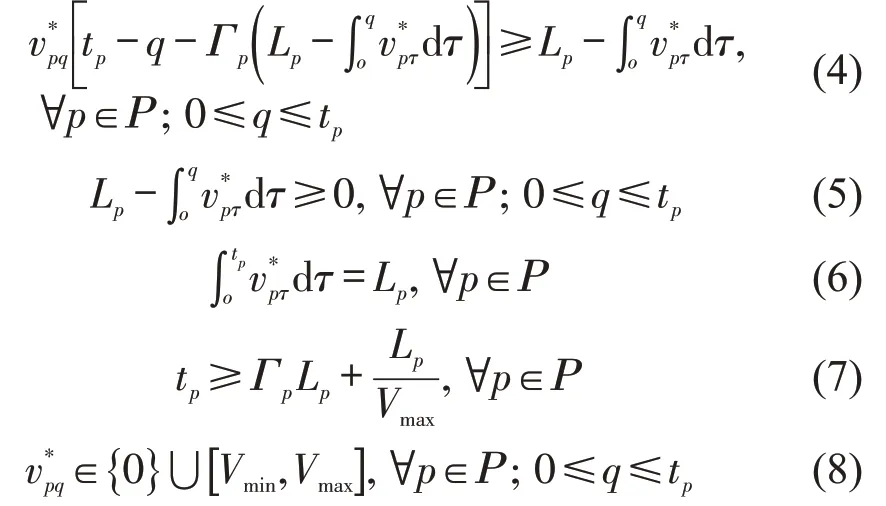
在M1 中，式(3)为航段燃油消耗最小；式(4)确保维持海上缓冲时间，式(5)和式(6)确保船舶在航行时间内到达下一港口；式(7)为船舶在各航段航行时间取值范围；式(8)为船舶航速取值范围。

2.3 船期鲁棒优化模型

根据问题描述，基于M1 得到的航段最小化燃油消耗量函数C(tp)，进一步以班轮运输服务航次总成本最小为目标，建立船期鲁棒优化模型M2。

目标函数为

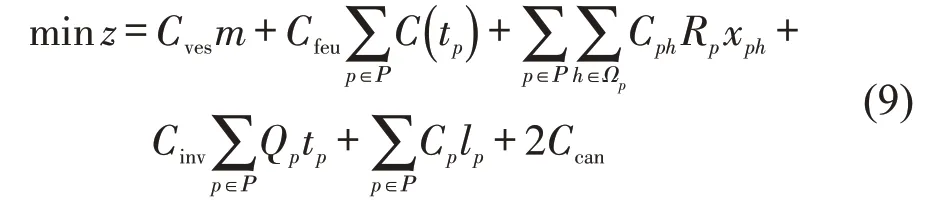
约束条件为

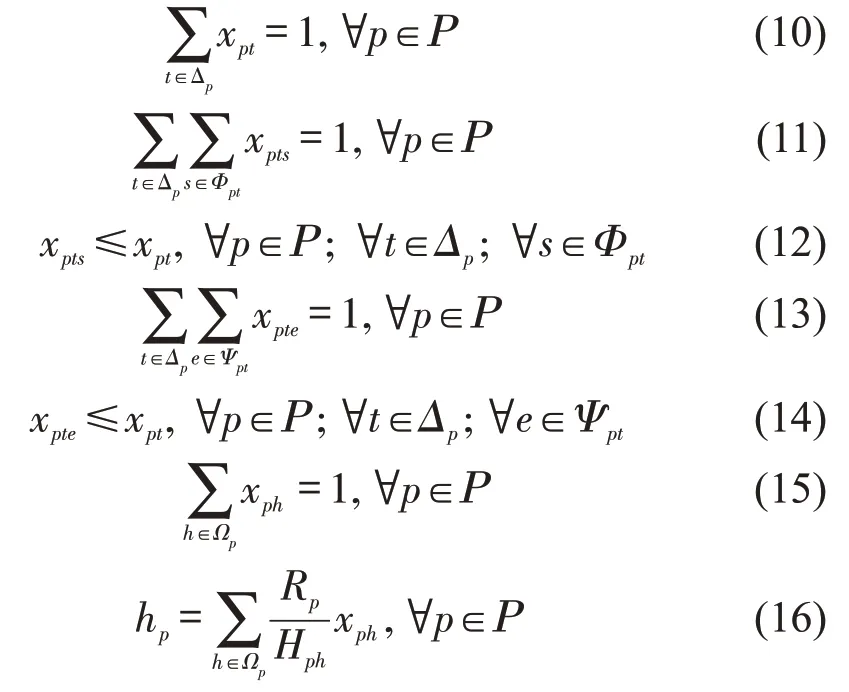
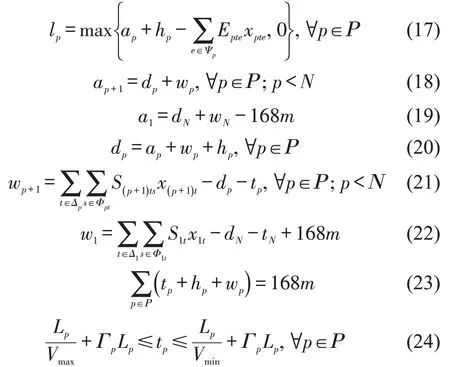
xpt,xpts,xpte,xph为0-1变量 ,

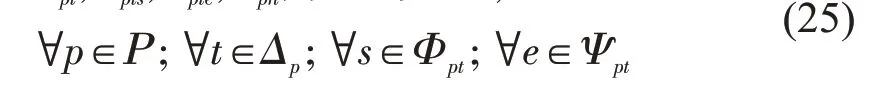
在M2 中，式(9)为班轮运输服务总成本最小化，其中，第1 项表示船舶运营成本，第2 项表示船舶航次燃油成本，第3项表示各港口装卸成本，第4项表示集装箱货物库存成本，第5项表示船舶迟到港口惩罚成本，第6项表示运河成本；式(10)～式(14)为船舶在港口的时间窗约束；式(15)和式(16)为船舶在港口的装卸时间约束；式(17)～式(20)为船舶到港、离港时刻约束；式(21)和式(22)为船舶在港口的等待时间；式(23)为船舶1 个往返航次总时间；式(24)为各航段船舶航行时间范围鲁棒性约束；式(25)为0-1变量约束。

3 算法设计

3.1 M1算法

M1 是连续最优控制问题的变体，可以用离散化逼近方法求解。为此，本文通过把船舶航段p的航行时间tp划分为多个等时区间，并假设船舶在每个区间内以恒速航行，将M1 进行转换并求解。具体步骤如下：

Step 1 把航段p的航行时间tp划分为λp个等时区间，并假设船舶在第ξ(ξ∈{1,…,λp})个区间内以恒速航行。其中，在航段p第ξ个时间区间开始时刻为，航段p剩余航行距离为，剩余航行时间为，剩余缓冲时间为Γp(Lp-Lpξ)。由此，在航段p第ξ个区间的航速为

Step 2 参照文献[6]，可得连续最优控制问题的优化条件为

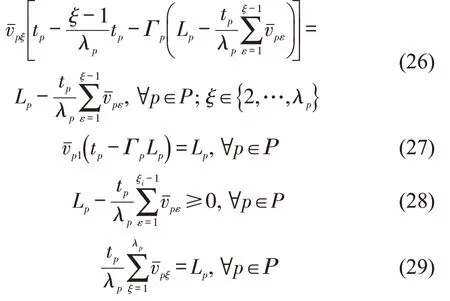
于是，将模型M1转化为模型M3。

目标函数为

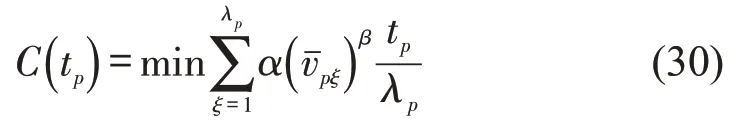
约束条件为式(26)～式(29)及

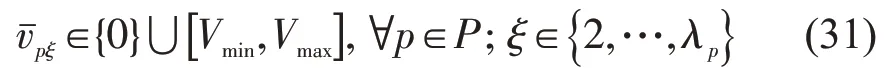
Step 3 若给定船舶在航段p航行时间tp，则在M3中，由式(27)可计算获得，由式(26)可依次计算获得其余的，∀p∈P,ξ∈{2,…,λp} 。

Step 4 由式(30)求解得到最小燃油消耗量函数C(tp)，∀p∈Ρ。

3.2 M2算法

由于M2 是一个非线性混合整数规划问题，难以直接求解。为此，本文通过将变量tp离散化，利用M3 在tp离散化取值时得到最小燃油消耗量函数的基础上，再对M2 进行线性化求解。具体步骤如下：

Step 1 将船舶在各航段航行时间tp的取值区间以分钟为时间单位划分成个等间隔小区间，其中，第j个小区间间隔点的值为j∈{0,1,…,Jp} 。

Step 2 令tp=Tpj，j∈{0,1,…,Jp} ，利用M3，便可求得最小燃油消耗量C(Tpj)。

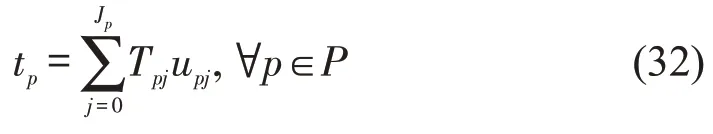
于是，模型M2转化为模型M4，即

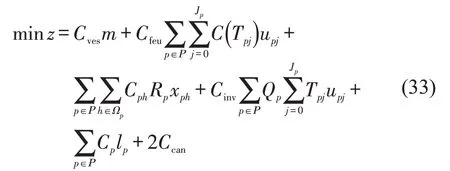
约束条件为式(15)～式(23)及

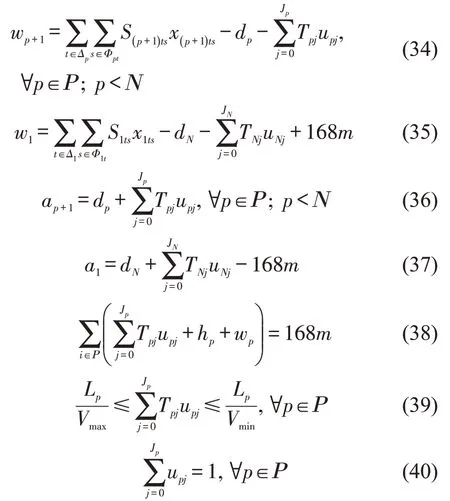
Step 4 利用商用软件求解混合整数线性规划模型M4，得到优化结果。

4 算例分析

4.1 数据选取

本文选取中国远洋海运集团有限公司(中远海运)经营的集装箱班轮运输AWE1 航线为例，航线配置载箱量为10036 TEU、最小和最大航速分别为15 kn和25 kn的多艘船舶，船舶通过巴拿马运河时间为15 h。该航线1 个往返航次船舶共挂靠12 个港口，其挂靠港口顺序如图2所示。

图2 AWE1航线Fig.2 Route of AWEI

由于在算例中不易获取各航段海上意外时间经验数据，故参照文献[6]，各航段船舶航行缓冲时间比例系数统一设定为0.01(h·(n mile)-1)；船舶燃油消耗系数数据取自文献[5]；船舶周运营成本、集装箱货物单位库存成本及燃油价格数据取自文献[4]；船舶延误单位惩罚成本数据取自文献[7]；船舶通过巴拿马运河的费用，各港口为船公司提供的4个时间窗，每个时间窗的3个开始和结束时刻，以及4 个装卸效率及对应的装卸成本数据取自文献[5]。由于OD流量数据属于商业秘密，故参照文献[5]，本文利用均匀分布分别随机生成各港口对间的集装箱OD流量数据，各航段的平均航速由均匀分布U[15,25] kn随机生成。结合船舶驾驶实际，本文假定每5 min为1个船舶航速调整区间。

4.2 计算结果

基于以上数据，本文利用均匀分布随机生成100 个参数场景，利用Gams 软件进行算例数值分析，得到1个往返航次的船舶到、离各港时间如表1所示。

表1 船舶到、离各港时间Table 1 Vessel arrival and departure time at each port（h）

由表1可见，船舶1 个往返航次的总时间为1344 h(8周)，配船数量为8艘。

将本文模型M2与文献[5]的模型M5(未考虑海上意外时间)及文献[6]的模型M6(无合作协议)进行算例对比分析，结果如表2所示。

由表2可知，本文模型M2 得到的班轮运输服务总成本最小，比M5 和M6 分别降低了14.65%和3.54%。究其原因，是由于与M5 相比，M2 通过为各航段预留船舶航行缓冲时间，使得当航段上海上意外时间造成航速减慢时，船舶有足够多的缓冲时间防止到港延误。而M5 船期设计的比较紧凑，在船舶航行中发生航速减慢时，就会导致即使在航段剩余航程上加快航速(增加燃油成本)和在下一港口选择较高效率进行装卸(增加装卸成本)，也会产生船舶迟到(增加迟到惩罚成本和货物库存成本)，同时，还容易降低客户服务水平；与M6相比，由于M2基于多时间窗、多起讫时刻和多装卸效率合作协议，使船公司可以灵活地选择合理的船舶到港、离港时间和装卸效率，从而有效地降低船舶迟到惩罚成本和装卸成本。

表2 成本对比Table 2 Comparison of costs（103 美元）

4.3 敏感性分析

本文对船舶航行缓冲时间比例系数进行敏感性分析，令Γ在0.006(h·(n mile)-1)～0.014(h·(n mile)-1)递增变化，构造9组算例，每组算例由100个随机生成的场景组成，求解得到班轮运输服务总成本和到港延误时间的敏感性，分析结果如图3所示。

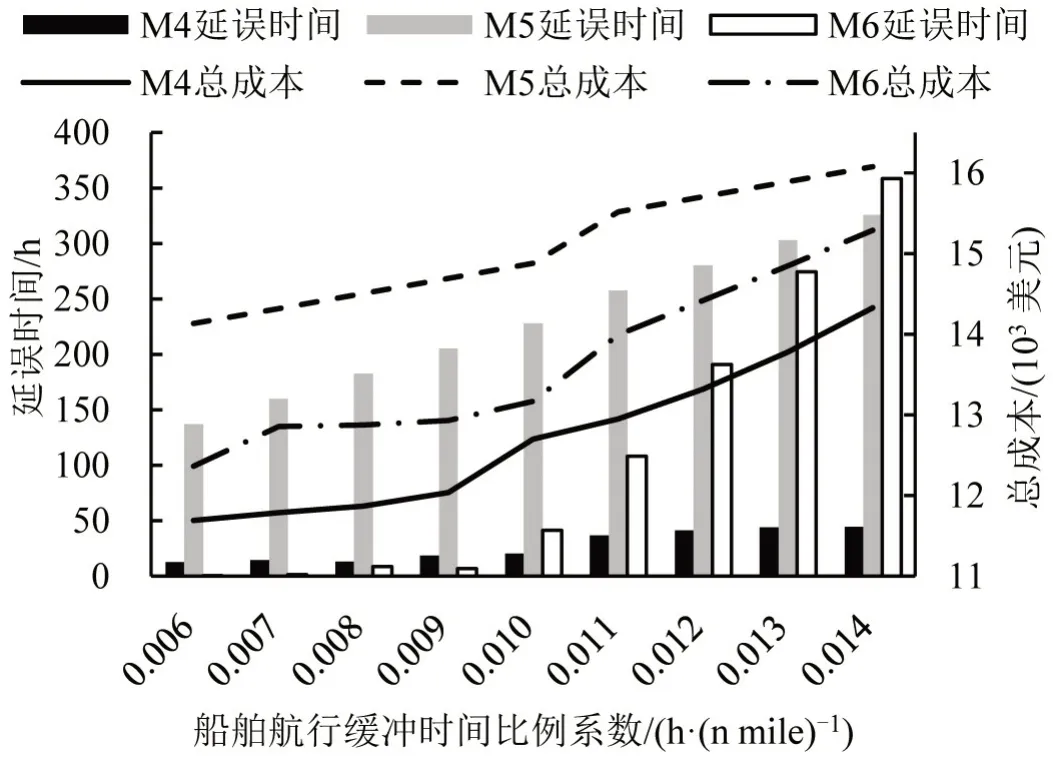
图3 比例系数的敏感性分析结果Fig.3 Sensitivity results of proportional coefficient

由图3可知，随着船舶航行缓冲时间比例系数的增大，M2、M5和M6得到的班轮运输服务总成本呈增加的趋势，本文模型M2 的结果始终最小；此外，M2、M5和M6得到的船舶到港延误时间也呈增加的趋势，在该系数超过0.01(h·(n mile)-1)时，M2得到的船舶到港延误时间始终最小，且随着该系数的增大，M2 的船舶到港延误时间始终呈现缓慢增加趋势，而M5 和M6 的船舶到港延误时间却呈现明显增加趋势。由此说明，海上意外时间越长，本文模型M2对降低班轮运输服务总成本和减少船舶到港延误的效果越显著。究其原因，是由于当航行缓冲时间比例系数增大时，为各航段按距离事先预留出的船舶航行缓冲时间越长，可以更有效地防止船舶到港延误，使船公司能够更灵活地调整航速，选择船舶到港、离港时刻和装卸效率。

5 结论

海上意外时间导致的船期不稳定，对船公司、港口及客户均造成极为不利的影响。本文基于合作协议，研究设计了考虑海上意外时间的船期鲁棒优化设计方案。结果表明，考虑海上意外时间，基于多时间窗、多起讫时刻和多装卸效率合作协议，开展鲁棒性船期设计，可有效地降低船公司班轮运输服务总成本，并减少船舶到港、离港时间延误对港口作业造成的不利影响，提高集装箱货物运送的准时率和客户满意率，实现班轮运输船公司、港口和客户三方共赢。