基于组合热源模型的中厚板MIG焊模拟

徐洲 李晓延 吴奇 王海东

摘要：为实现对复杂形状熔池下中厚板MIG焊过程的准确模拟，通过提取焊缝熔合线，拟合多项式方程，建立了具有特殊空间分布的电弧+熔滴组合热源模型。分别基于该模型和双椭球热源模型对6 mm厚6082-T6铝合金MIG焊进行了有限元模拟，计算了焊接温度场和焊后应力场。结合两种热源模型的模拟结果，从实际焊缝形状、热循环曲线、应力分布测量值三方面进行对比分析。结果表明，组合热源模型调节参数少，其温度场能更好地反映复杂形状熔池，应力场与实测值吻合度更高，适合开坡口的中厚板MIG焊过程模拟。

关键词：焊接模拟;热源模型;熔合线;中厚板

中图分类号：TG402      文献标志码：A         文章编号：1001-2003（2021）11-0044-06

DOI：10.7512/j.issn.1001-2303.2021.11.08

0 前言

铝合金因比强度高、耐腐蚀、高温性能好等特点，现已广泛应用于高速列车、航空航天等工业制造领域[1]。焊接作为一种主要的连接方法，在铝合金加工中占据着重要地位。焊接结构是工件的薄弱环节，通过有限元手段模拟焊接过程，能够快速全面地分析焊后应力分布[2]。

焊接有限元模拟的仿真精度在很大程度上取决于所采用的热源模型[3-4]。在铝合金中厚板焊接中，为保证单面焊双面成形往往需要开坡口，加上较大的热输入，使得最终熔池形状复杂，而已有的单一热源模型熔池模拟结果一般接近于半椭球、锥形等有限种类的熔池形状，使得模拟精度下降[5-6]。为了解决复杂熔池条件下传统单一热源难以匹配的问题，研究人员做了大量工作。Wu[7]等针对等离子弧焊过程的特点，建立了双椭球体+二次锥体的组合热源模型，并根据小孔深度的变化动态调整其分布参数;马悦[8]通过调整不同方向的热流密度分布参数值，得到焊缝成形系数较小的“ 柱状 ”熔池和成形系数较大的“ 碗状 ”熔池;李振江[9]对比了两种组合热源模型，最后选择工件的上部采用双椭球体热源，下部采用圆柱体热源。上述研究最终都获得了与各自熔池形状相符合的模拟结果，但是过于依赖热源参数的调整或者使用组合热源模型时引入了更多的热源参数，增加了模拟工作量。Wang[10]等提出了一种直接提取实验熔合线的旋转体热源，减少了热源参数，能够适应多种焊接方法的熔池形状，但是仅以形状匹配为参数调节标准，未考虑实际能量输入。

针对以往组合热源模型存在的调节参数过多、未考虑实际热输入等问题，文中在提取实验熔合线的旋转体热源基础上，开发了高斯面+双旋转体新型组合热源模型，并结合焊缝横截面宏观金相、温度曲线和应力测量结果，与传统双椭球热源进行对比，实现了热源参数调整的简化和6 mm厚铝合金板MIG焊的准确模拟。

1 实验材料与方法

1.1 焊接实验

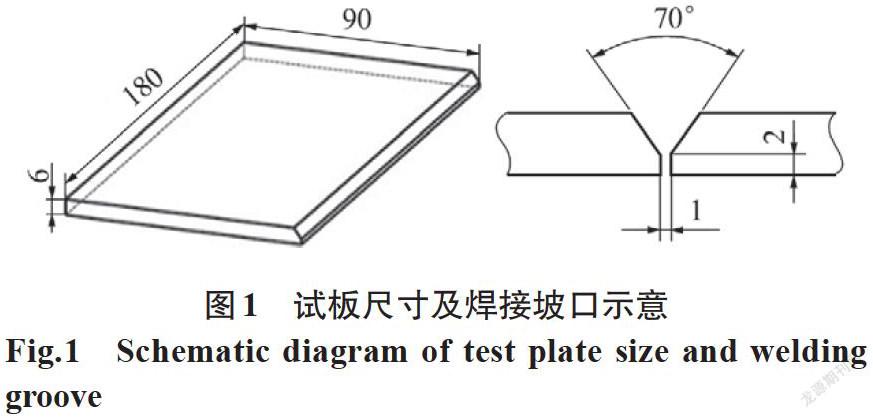
采用MIG方法对接焊接6 mm厚的6082-T6铝合金平板，采用福尼斯TPS 5000焊机，焊接材料为φ1.2 mm的ER5356焊丝，焊接过程通氩气保护，焊接参数为：电流175 A、电压23 V、焊速0.5 m/min。平板尺寸和坡口形式如圖1所示。

1.2 热循环曲线记录和残余应力测试

在焊接试板中心横截面与上表面交线上且距焊接坡口端10 mm以及15 mm位置处分别布置K型热电偶，采用UT-325测温仪实时记录焊接过程中特征点的温度数据，生成热循环曲线。焊后采用iXRD-MG40P型X射线衍射应力仪测量残余应力。

2 有限元模拟

2.1 网格划分

使用有限元软件Abaqus建立试板模型。由于平板对接中焊缝两侧的约束及边界条件对称，为节省计算时间，只模拟其中一侧。综合考虑计算准确度和计算效率，网格划分从焊缝到边缘由密到疏，网格模型如图2所示。

2.2 热源模型

热源模型的建立需要确定热流“ 以何种空间形式分布 ”和“ 以何种分布模式分布 ”两个要素[11]。其中“ 热流分布的空间形式 ”一般对应着不同焊接方法下的熔池形状特点，比如适用于大多数半椭球熔池的双椭球热源模型，针对电子束焊钉子状熔池的旋转高斯体热源模型[6，12]。在模拟结果的准确性评价中也多采用熔池边界准则，即在一定的焊接热输入条件下，模拟计算获得的熔池轮廓与试验所测相吻合，则证明所建立的热源模型是准确的[13]。以上经验说明，热源模型的空间形式需要从熔池形状出发。而在开坡口的中厚板MIG焊中，熔池形状复杂，传统热源模型不能反映该熔池形状，虽然有研究者通过结合多种传统热源的组合热源最终接近了熔池形状，但是大大增加了需要调节的形状参数，使得热源校准过程繁琐。基于此，文中在MIG焊模拟的热源模型中直接代入实验测得的焊缝熔合线，使输入热流分布在近似的实际熔池范围中;在“ 热流的分布模式 ”这一要素处理中，将焊接能量分为电弧和熔滴两部分，根据焊接参数分配热输入，建立组合热源模型。

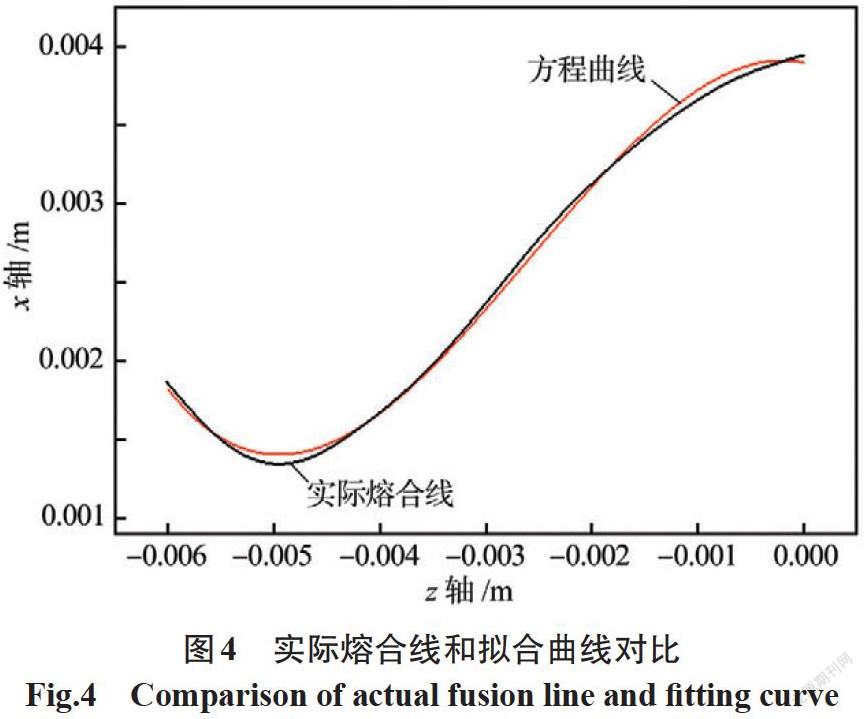
（1）以双旋转体均匀热源表示熔滴带入的热量。建立过程如下：首先取得实际的焊缝横截面熔合线轮廓，代入图像处理软件，建立坐标系，如图3所示，深度方向为自变量数轴z轴，水平方向为因变量数轴x轴，提取熔合线上的11个点坐标。

获得坐标后，在Origin中通过多项式拟合获得相应的多项式方程为x=-46 834z3-362.77z2-0.143 6z+0.003 9。该方程表示的曲线即为数学拟合出来的实际熔合线轮廓，其线形对比如图4所示。可以看出，采用三次多项式方程已经能够很好地表示焊缝熔合线，方差数值显示为0.998，说明拟合度较高。

下一步，以多项式方程曲线为边界构建旋转体，如图5a所示，以z轴为旋转轴，曲线旋转一周得到旋转体。将旋转体沿y轴（热源移动方向）拉伸一定倍数k，得到拉长的旋转体。类似双椭球热源模型，焊枪前端为拉伸前的旋转体的1/2（图5a中深色部分），后端为拉伸后的旋转体的1/2（图5b中深色部分），这一双旋转体空间（见图6c）就是熔滴热流分布的区域。

确定热源模型的空间形式后，还需确定热流“ 以何种分布模式分布 ”，即组合热源中各单一热源的热输入以及分布模式。MIG焊中熔滴热输入为

式中 ρ为焊丝密度，ρ=2 712 kg/m3;rw为焊丝半径，rw=0.0006 m;ω为送丝速度，ω=0.188 3 m/s;Hd为焊丝熔化热焓，焊丝从常温加热至2 000 ℃时 Hd=2 638 J/g[14]，计算可得Qm≈1 524 W。

热源模型中最常用的分布模式为高斯分布，其来自于对TIG焊电弧热分布的实验观察，而MIG焊过程中的熔滴进入有着快速搅拌效应的熔池，热量迅速均匀化，应假设热量均匀分布在双旋转体中，则该体中任意位置热流密度等于Qm/V，V为双旋转体的体积，可由式（2）计算得出。

熔滴热源模型建立完成，其热流分布在考虑实际熔合线的双旋转体中采用均匀分布模式，热输入由焊丝参数和送丝速度计算得出。

（2）以高斯面热源表示电弧带入的热量。半径为r的圆上热流密度呈高斯分布。电弧输入功率由总的热输入去除焊丝熔化功率获得，即Qa=ηUI-Qa，η为焊接热效率。

最终的组合热源热流密度分布表示为：

为了验证组合热源的准确性，同时还选择了双椭球热源进行模拟，表示为

式中 a、c、bf、br均为形状参数，分别指椭球的宽度和深度、前后半球的长度;ff、fr为前后半球的能量分配系数。

2.3 计算过程

为了得到准确的温度场计算结果，正式计算前需要以实际熔池形状为参考，试计算调整热源模型形状参数，双椭球热源模型的形状参数有a、c、bf、br，组合热源模型只有r。

确定热源参数后，分别代入两种热源模型。采用顺序耦合，即先计算温度场，再以温度场计算结果为初始条件计算应力场。

3 结果与分析

3.1 熔池形状与焊缝形貌对比

在温度场模拟结果中，输入铝合金熔点（660 ℃），得到模拟的熔池范围如图6所示。可以看出，组合热源模型中的熔滴热源模型部分由于代入了实际焊缝熔合线，即使在不包含形状参数、无参数校准步骤的情况下，仍然很大程度接近实际熔池形状，而双椭球热源受限于自身热流分布表达式，在不断调整形状参数后，熔深与表面熔宽能够符合真实情况，但熔合线以及下部熔宽与实际焊缝差别很大。组合热源模型能够调节深度方向的热流分布，考虑了熔池内部和熔池表面的差异。

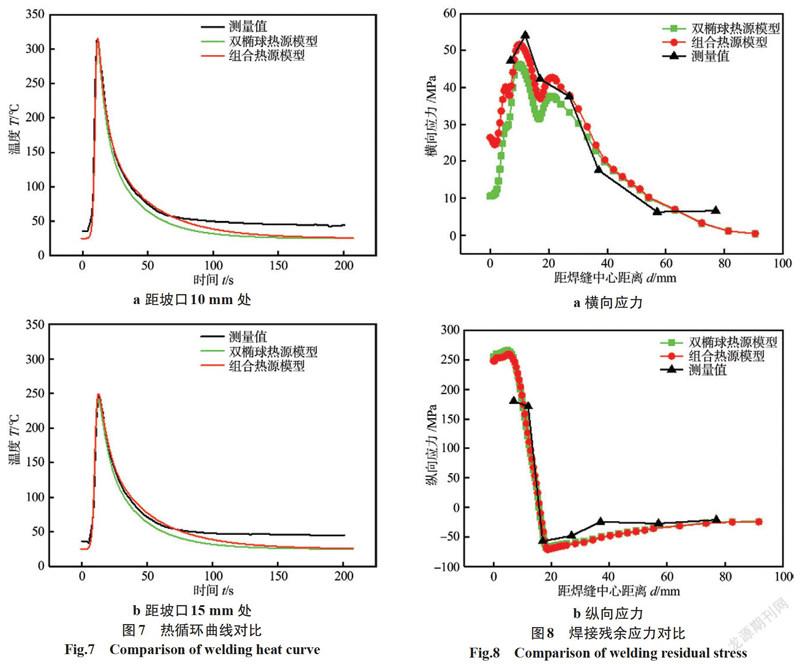
3.2 热循环曲线对比

选择热电偶测温对应点的温度变化历程，热循环曲线对比如图7所示，距离焊接坡口端10 mm和15 mm处特征点的焊接过程峰值温度分别为313.9 ℃和245 ℃。由图7可知，两种热源模拟的升温速率、峰值温度与实测值均较为一致;但在降温阶段，组合热源的降温速率和实际降温趋势更为吻合，这是因为在模拟熔池表面，组合热源模型热量来自于电弧热源和熔滴热源的共同作用，而双椭球热源模型只对它们进行了简单的统一处理;由于测温前工作台已经进行过数次焊接实验，使得压板、垫板温度较高，在75 s后的降温部分，模拟结果均与实测值有一定偏差。总的来看，组合热源的温度曲线与测温曲线更加符合，这是因为对电弧和熔滴能量分开考虑，并为它们选择了不同的热流分布模式，使得模拟热输入更加科学，更符合有熔滴过渡行为的MIG焊特点。此外需要说明的是，由于测温点设置在试板表面，温度曲线与焊接上部熔池较为相关，而从模拟熔池来看，双椭球热源在下部熔池的误差更大，可以推断组合热源模型在深度方向的温度场准确性具有更大优势。

3.3 残余应力对比

在应力场计算结果中，建立横向路径，模拟应力分布和实测值对比如图8所示。由图可知，横向应力的模拟值和实测值均呈拉应力分布，在距焊缝中心0～40 mm范围内，组合热源模型的应力水平更高，与实测值更为接近，远离焊缝区域，两种模型的横向应力差别不大。图8b为纵向应力沿横向分布，两种模型的模拟结果十分接近，均与实测值趋势相吻合。总的来看，双椭球热源模型和新型组合热源模型均能够模拟焊后应力場，应力分布趋势与实测值一致，但组合热源模型在靠近焊缝的横向应力模拟中具有更好的模拟精度。

4 结论

（1）高斯面+双旋转体组合热源模型能够模拟带有坡口的中厚板焊接温度场，模拟熔池形状与焊缝形貌相符。

（2）在有熔滴过渡行为的MIG焊模拟中，根据熔滴和电弧建立组合热源，相较传统的单一热源，能够获得更准确的应力模拟结果。

（3）在热源模型的建立中代入焊缝熔合线，能够在保证模拟准确度的同时减少热源参数校准工作。

参考文献：

吴奇，李晓延，王小鹏，等. 热处理工艺参数对2219铝合金焊接接头残余应力的影响[J]. 热加工工艺，2021，50（1）：131-135.

Du Pengfei，Chen Weishan，Deng Jie，et al. Effects of knurl tooth angle on mechanical and thermal behaviors of aluminum ultrasonic welding[J]. Ultrasonics，2020：108.

Chen Yuxi，He Yinshui，Chen Huabin，et al. Effect of weave frequency and amplitude on temperature field in weaving welding process[J]. Springer London，2014，75（5）：803-813.

Ke Wenchao，Bu Xianzheng，Oliveira J P，et al. Modeling and numerical study of keyhole-induced porosity formation in laser beam oscillating welding of 5A06 aluminum alloy[J]. Optics & Laser Technology，2021（133）：1-10.

Chukkan J R，Vasudevan M，Muthukumaran S，et al. Simulation of Laser Butt Welding of Aisi 316l Stainless Steel Sheet Using Various Heat Sources and Experimental Validation[J]. Journal of Materials Processing Tech.，2015：219.

Velaga Satish-K，Ravisankar A. Finite element based parametric study on the characterization of weld process moving heat source parameters in austenitic stainless steel[J]. International Journal of Pressure Vessels and Piping，2017（157）：63-73.

Wu C S，Zhang T，Feng Y H. Numerical analysis of the heat and fluid flow in a weld pool with a dynamic keyhole[J]. International Journal of Heat and Fluid Flow，2013（40）：186-197.

马悦. 双椭球焊接热源模型一般式的数值模拟研究[D]. 河北：河北工业大学，2015.