长宁超长水平井钻井摩阻数值模拟分析

李文哲，代 锋，曾 光，宁松岩，薛宪莹，阳文发，李 柯

1四川长宁天然气开发有限责任公司 2安东石油技术(集团)有限公司 3西南石油大学

0 引言

“超长水平井”一般认为是指水平段长大于3 000 m的水平井，可以实现1个井筒动用相当于2口井地下资源的目标，是提高单井产能、单井最终累计采出气量和提升经济效益的重要手段[1-3]。但同时给钻井施工带来一系列难题，如摩阻、扭矩将增大，对钻杆的抗拉、抗扭要求更高；水平段长，井眼清洁难度增大；井壁失稳风险增高，卡钻风险变大等[4-5]。

在高德利提出“井工厂”这一高效的页岩气开发模式以来[6]，大量学者从增加井场布井数量和水平井延伸长度这两个方面来研究页岩气开采如何实现降本增效。国外，Alfsen等[7]对部分长水平段钻井作业历史案例进行分析比较，主要从模拟钻井和实际钻井的参数进行对比。Mason等[8]通过案例对延伸钻进极限作业进行了讨论与展望。Allen等[9]从井身结构、定向控制、水力参数、井眼清洁和摩扭等方面对延伸钻进作业进行了全面分析。国内，高德利等[10]最早提出了详细的延伸钻进极限基本概念。汪志明等[11]根据大位移井的水力学原理，分析了岩屑床、泵功率以及环空压耗对大位移井水力延伸极限的影响规律，分析结果表明延伸极限与地层安全密度窗口和额定泵压成正相关，与环空压耗和岩屑床高度呈负相关。连威等[12]研究了高温高压情况下钻井液的密度与流变性计算模型，提高了高温高压环境下延伸钻进极限的计算精度。闫铁等[13]根据大位移井的实际参数，应用整体钻柱摩阻分析的间隙元理论，给出了大位移井的延伸极限判断准则和计算模型，得出了影响延伸钻进极限的因素从大到小依次为摩阻系数、井眼曲率、门限钻压和钻盘转速这一重要结论。罗伟等[14]分析了影响延伸钻进极限的几个主要因素，分别为钻机性能、泵性能、钻柱强度、目的层承压能力和井眼清洁能力。刘茂森等[15]根据长宁页岩气的钻井实际，分析了钻机承载、钻柱安全系数、地层承压能力和额定泵压等因素对水平井延伸钻进能力的影响。

业界对长水平段钻井以及延伸钻进做了大量研究。本文基于钻柱动力学模型，研究了井眼轨迹和钻具组合对摩阻扭矩的影响，为作业现场实施降摩减阻提供了理论指导。

1 CN-H21-5井基本情况

CN-H21平台位于四川省宜宾市兴文县，构造位置位于长宁背斜构造中奥顶构造南翼，构造主体区断层不发育，钻探目的层为志留系龙马溪组。该区块内地层层序正常，自上而下依次为三叠系、二叠系和志留系。目的层为龙一1亚段沉积外陆棚亚相黑色含硅碳质页岩、富有机质黑色碳质页岩，分布较稳定，有机质丰富，孔隙度和含气量都较高。CN-H21-5井是部署在本平台的一口超长水平开发井，设计井深为5 740 m，水平段长为3 000 m，井斜为84.38°；实际完钻井深为5 750 m，水平段长度为3 070 m；井斜为86.97°。CN-H21-5井井身结构如表1所示。

表1 CN-H21-5井井身结构

该井的施工难点主要有以下两点：① 水平段较长，钻具与井壁间的摩阻较大，钻压难以传递到钻头处；② 钻柱需要传递较大的轴向力来克服钻具与井壁间的摩阻，从而导致钻柱容易发生屈曲变形。

2 超长水平井摩阻扭矩分析方法

全井钻柱按弹簧—质量—阻尼系统(S-M-C模式)考虑，采用有限元思想，将无限自由度的问题转化为有限自由度问题进行求解[16-20]。

2.1 全井钻柱动力学模型

钻柱动力学模型是基于能量法中的哈密顿(Hamilton principle)原理建立的。该原理指出：运动质点动能、势能和非有势力做功应该满足如下公式：

(1)

式中:W—非有势力做功,J；δ—变分算子；T—系统总动能,J；V—系统总势能,J。

式(1)中的T-V为拉格朗日函数(L)，在钻柱系统中，钻柱的运动位移u(z,x,y,t)和转角变量θ(z,x,y,t)可以分别用T、V和W表示。在有限元法中将钻柱几何模型视为一个集合，钻柱各个单元包含于集合之中，模型中连续变量由所有单个钻柱单元的节点变量Ui代替(以内插值替换)。将其代入式(1)并逐步展开得到：

(2)

式中:Fi—系统广义非有势力,N；Ui—系统广义位移,m。

分析计算时，采用弹簧—质量—阻尼(S-M-C)系统，基于非线性动力学基本原理，建立钻柱系统的动力学方程，如式(3)。在引入边界和载荷条件后，采用常见的二阶偏微分方程数值解法中的HHT-α法对钻柱动力学方程进行求解，完成钻柱系统动力学分析。

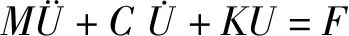
(3)

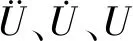
在井筒内部，钻柱的运动形态分为两种：自由运动状态,如图1；钻柱与井壁接触状态,如图2。

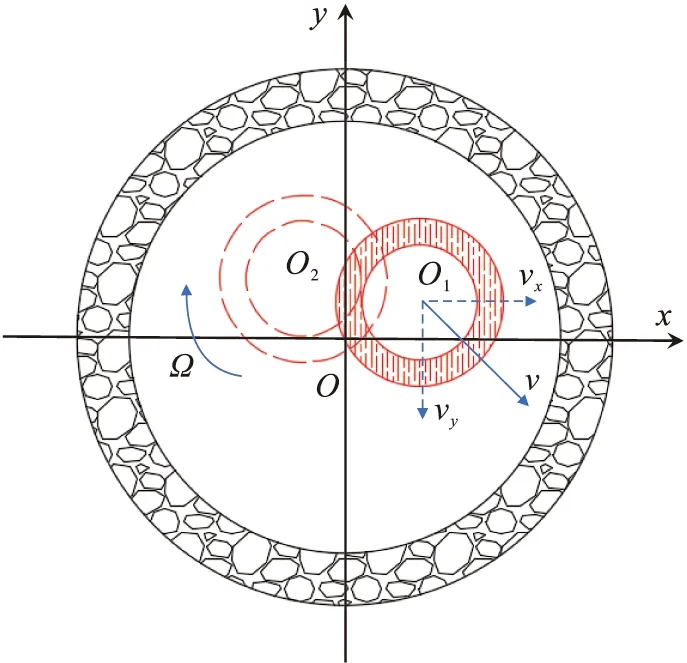
图1 钻柱自由运动状态图

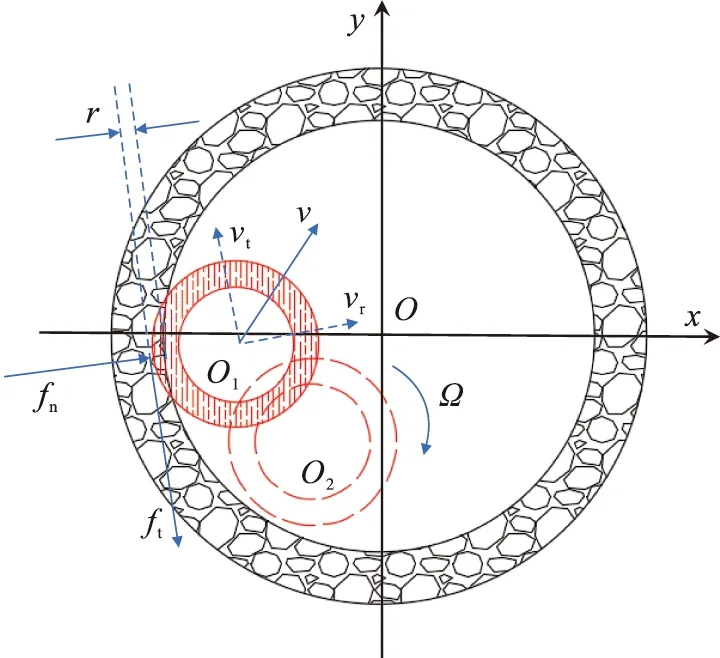
图2 钻柱与井壁接触状态图

钻柱与井壁未接触时，钻柱在井筒内自由运动，不会受到井壁给予的约束反力，处于自由运动状态；当钻柱与井壁临近，且其有向壁外运动趋势时，运动会受到井壁的束缚，表现为钻柱与井壁之间的碰撞，并产生接触和摩擦；当钻柱与井壁发生碰撞时，在接触位置会产生法向接触反力fn，以及在接触点处产生切向摩擦力ft、轴向摩擦力f等。

为了判断是否发生碰撞以及计算碰撞后接触力的大小。在钻柱与井壁之间构建接触元，接触元的厚度为0.001 m，则可以求得钻柱与井壁之间的互作用距离为：

(4)

通常采用赫兹接触理论来计算接触点处钻柱与井壁之间的接触力，设地层与钻柱的阻抗系数为k，阻尼系数为c，可求得钻柱与井壁之间的相互作用力为：

fn=kr+cvr

(5)

式中：r—钻柱与井壁之间的趋近距离,m；rd—钻柱单元节点的径向位移,m；Rw—井壁外径,m；fn—接触力,N；vr—钻柱节点处的径向速度,m/s。

由库伦摩擦定理可得，钻柱接触点处产生的摩擦力为：

f=-sign(v)ufn

(6)

ft=-sign(vt)utfn

(7)

式中：f—轴向摩擦力，N；u—轴向摩擦系数,无量纲；v—轴向速度,m/s；ft—切向摩擦力,N；ut—切向摩擦系数,无量纲；vt—切向速度,m/s。

2.2 仿真建模方法

利用有限元软件的预处理模块，建立三维有限元模型，如图3所示。采用空间双节点梁单元BEAM31、刚体壳单元R3D4、刚体壳单元R3D4和三维实体C3D8R分别对钻柱、井壁、钻头和井底岩石进行建模。采用数值计算方法，并通过工作站进行长时间计算，便可得到钻柱系统的运动受力情况。

模型中假设：① 分析过程中钻柱处于线弹性状态，不考虑塑性变形；② 初始时刻，钻柱的轴线与井筒轴线重合；③ 井筒假设为刚体，与钻柱发生接触时不产生变形。

图3为全井钻柱动力学模型的示意图。为了与现场的施工方式一致，将模型的井口边界设置为悬挂钻柱，在钻柱上施加上提力和转速。井底PDC钻头在下部钻具组合的带动下自由切削岩石。

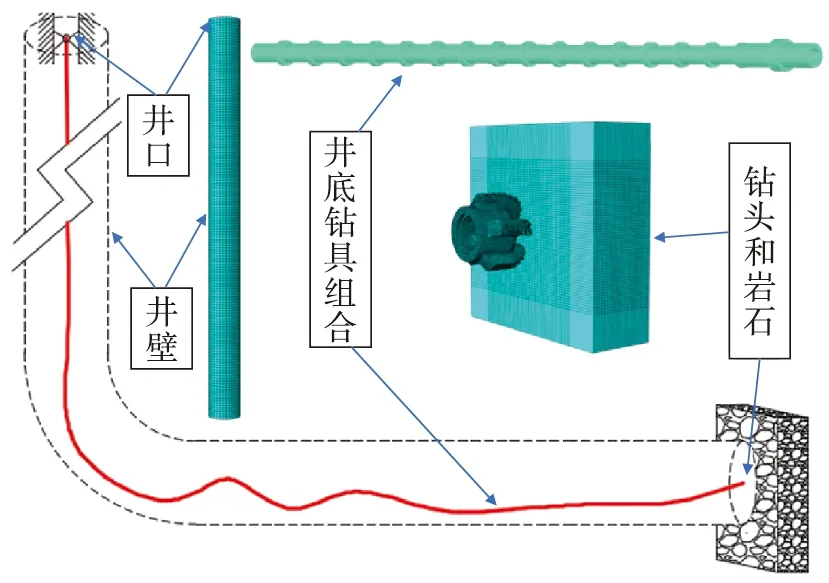
图3 全井钻柱动力学模型示意图

3 摩阻优化

3.1 井眼轨迹优化

水平井井眼轨迹优化，能够在一定程度上降低钻柱与井壁间的接触力，从而达到降摩减阻效果。与接触摩阻相关的水平井的轨迹优化重点以优化造斜段的造斜率为主，此处分别研究了造斜率4°/30 m、5°/30 m和6°/30 m时钻柱与井壁的接触摩阻。

从图4～图6可以看出，当造斜段造斜率为4°/30 m、5°/30 m和6°/30 m时，整体表现为造斜段后半段的接触力最大，接触摩阻最为严重，这是因为造斜段后半段钻柱位于造斜段和稳斜段交界处，受到两端钻柱挤压所导致的；而造斜率分别为4°/30 m、5°/30 m和6°/30 m时造斜段接触力总值分别为171.90 kN、110.26 kN和81.09 kN，即随着造斜率的增加，造斜段段长减少，造斜段的接触摩阻总值显著降低。

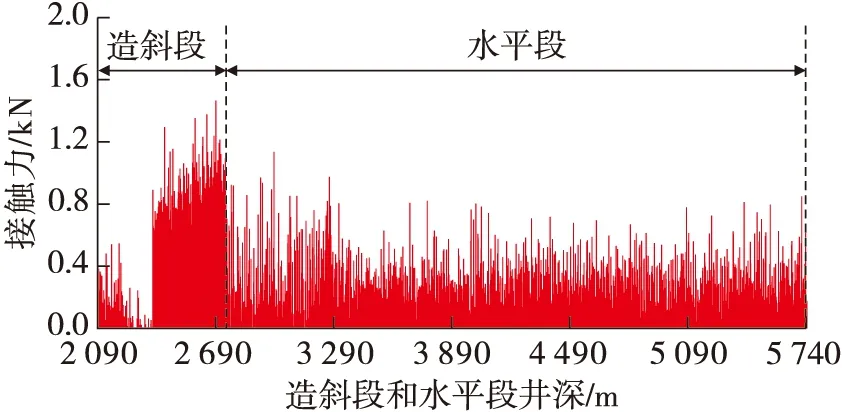
图4 造斜率4°/30 m钻柱与井壁的接触分布

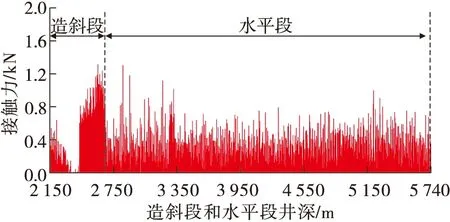
图5 造斜率5°/30 m钻柱与井壁的接触分布

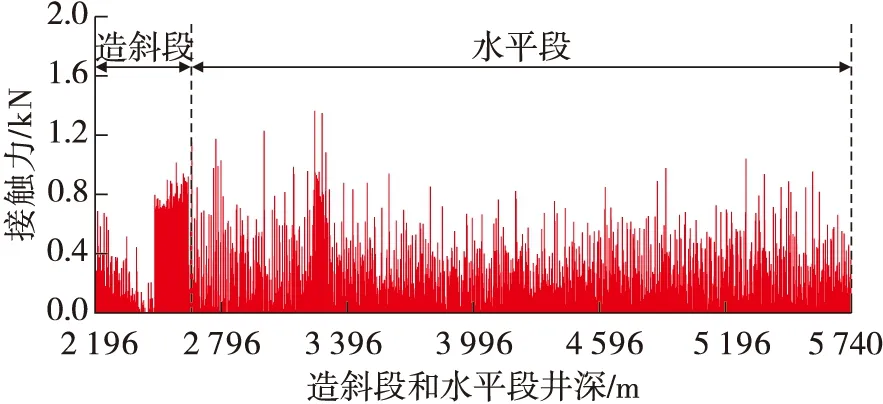
图6 造斜率6°/30 m钻柱与井壁的接触分布

当造斜段造斜率分别为4°/30 m、5°/30 m和6°/30 m时，计算得水平段接触力总值分别为393.56 kN、407.78 kN和414.94 kN。可见，当水平段段长增加后水平段接触摩阻总值将上升，但上升值明显低于造斜段减少的接触摩阻。因此，提高造斜率能够整体降低钻柱与井壁间的接触力，从而实现降摩减阻的效果。

当造斜段造斜率分别为4°/30 m、5°/30 m和6°/30 m时，水平井造斜段接触力总值加水平段接触力总值总和分别为565.47 kN、518.04 kN和496.03 kN。采用6°/30 m造斜率相较于4°/30 m造斜率的钻柱与井壁间的接触摩阻降低了12.28%，降摩减阻效果明显。

图7为造斜段造斜率4°/30 m～9°/30 m时，造斜段长度和造斜段接触力的变化情况。从图7中可以看到，随着造斜率的增加，造斜段长度的下降趋势逐渐放缓，同时，造斜段的接触力下降程度也逐渐降低。因此，在造斜段造斜率较小时增加造斜率，可以大幅降低造斜段长度，实现有效的降摩减阻。

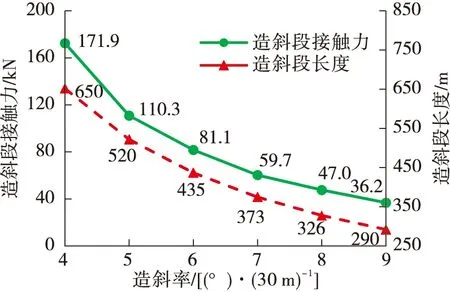
图7 不同造斜率情况下的造斜段长度和接触力大小

3.2 钻具组合优化

钻具组合是影响超长水平井摩扭的主要因素之一，优化钻具组合可以起到有效降摩减阻的作用。以往研究发现，相较于大尺寸钻柱，小尺寸钻柱凭借自身重量较轻的优势实现降摩减阻。但是，在超长水平井中，需要传递较大轴向力，小尺寸钻柱易发生屈曲变形，增大了钻柱与井壁间的接触面，摩阻大幅度上升，导致小尺寸钻柱丧失降摩减阻的优势，甚至发生钻柱螺旋锁死现象[17]。

图8～图10为水平段钻柱与井壁间的接触力分布情况。由图8显示，当水平段采用Ø139.7mm钻杆时，水平段的接触力总值为415.86 kN;图9显示，水平段采用Ø127 mm钻杆时，接触力总值为493.57 kN。原因在于Ø127 mm小尺寸钻杆在水平段前半段发生了严重屈曲变形，该处的接触摩阻急剧上升，在水平段未发生屈曲变形的后半段单节点接触力平均值为0.23 kN，较Ø139.7 mm钻杆在水平段后半段的单节点接触力平均值0.27 kN有所降低，但降低值不大。所以，在水平段全井段使用小尺寸的钻杆，接触摩阻相较Ø139.7 mm钻杆不减反增。

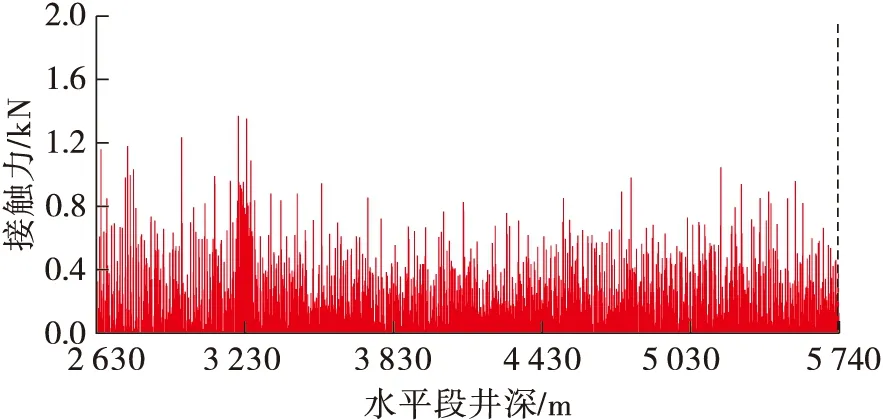
图8 水平段全部使用Ø139.7 mm钻杆时的接触力分布

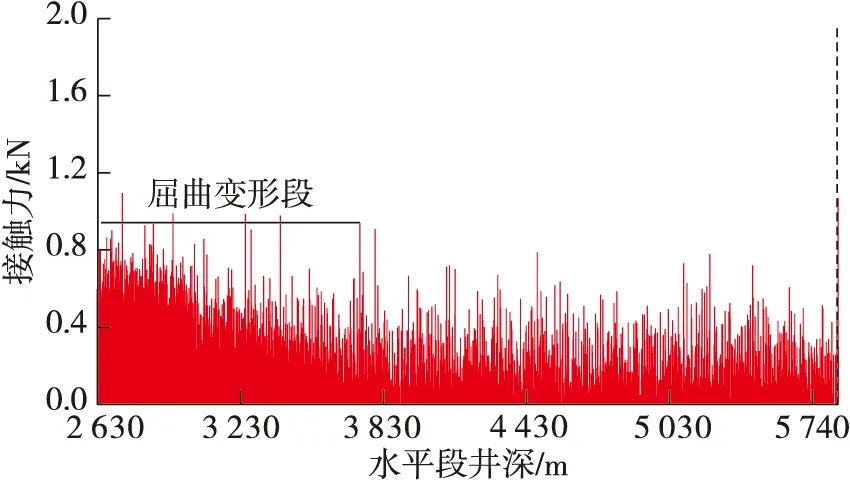
图9 水平段全部使用Ø127 mm钻杆时的接触力分布

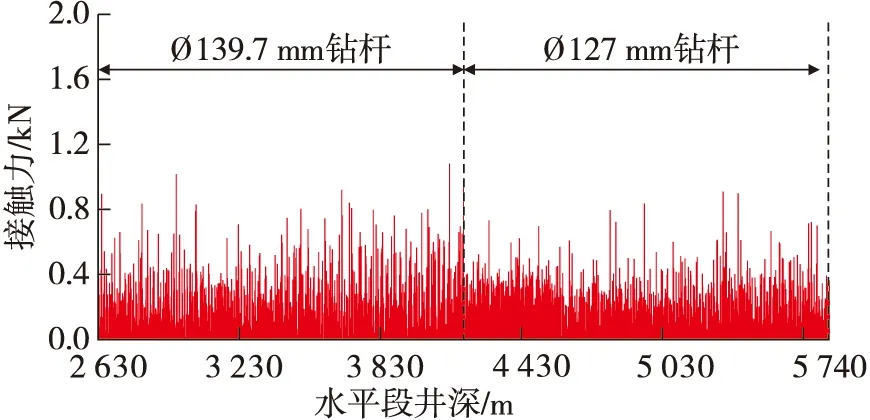
图10 水平段使用Ø139.7 mm+Ø127 mm钻杆时的接触力分布

为降低摩阻的同时控制钻柱屈曲变形，优化水平段钻具组合为“大+小”模式，即水平段前半段采用Ø139.7 mm钻杆抵挡屈曲变形，满足钻柱传递较大轴向力的需求，在水平段后半段采用Ø127 mm钻杆达到降摩减阻效果。组合钻具产生的接触力计算结果如图10所示，接触力总值为376.25 kN，相较于水平段全采用Ø139.7 mm钻杆降低了9.52%，同时避免了钻具发生屈曲的风险。

3.3 现场应用情况

根据井眼轨迹优化结论，在CN-H21-5井造斜作业时采用≥5°/30 m的造斜率，根据井口和目标靶体位置，本井井眼轨迹设计三维轨迹。根据上部地层自然造斜能力、横向靶前距、靶体倾角等因素，本井井眼轨迹剖面方案为：在石牛栏组可钻性较好的井段(1 550 m)提前造斜，以6.53°井斜稳斜到2 234 m，满足横向位移要求；穿过石牛栏组后开始第二次造斜，采用边扭方位边增斜模式，造斜率控制在5.5°/30 m左右；钻达入靶点后井斜角达到84.38°，稳斜钻至出靶点。水平段井斜角根据地质导向师临时指令实时调整。该井井眼轨迹剖面优化结果如表2所示。

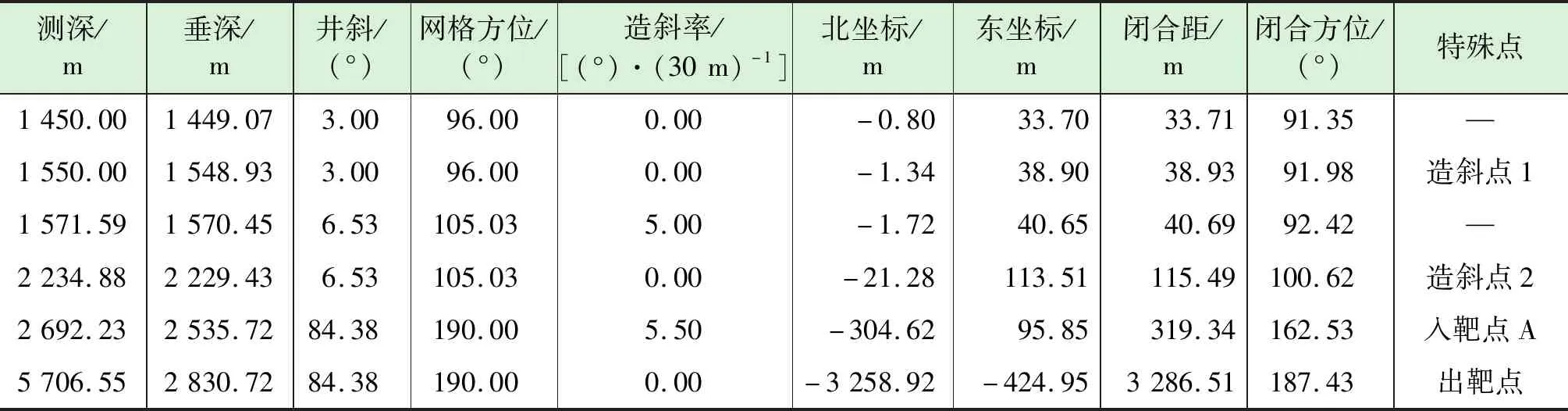
表2 井眼轨迹优化结果

根据钻具组合优化结论，在水平段采用“大+小”的钻具组合，即在水平段前半段采用Ø139.7 mm钻杆来抵挡屈曲变形，在水平段后半段采用Ø127 mm钻杆实现降摩减阻。具体钻具组合如下：

(1)韩家店—石牛栏组：Ø215.9 mm PDC钻头+Ø172 mm高效螺杆+浮阀+定向接头+无磁钻铤(MWD随钻测斜仪)+井下滤网短节+Ø127 mm加重钻杆+随钻震击器+Ø127 mm加重钻杆+Ø127 mm钻杆(造斜段)+变扣接头+Ø139.7 mm钻杆(直井段)。

(2)龙马溪组(双动力Archer旋转导向)：Ø215.9 mm钻头+PD Archer+定向短节+通讯短节+MWD随钻测斜仪+柔性短节+大扭矩螺杆+井下滤网短节+循环阀(多次开关)+Ø127 mm加重钻杆+随钻震击器+Ø127 mm加重钻杆+Ø127 mm钻杆(水平段后半段)+变扣接头+Ø139.7 mm钻杆(水平段前半段、直井段)。

(3)龙马溪组(备用—常规定向)：Ø215.9 mm PDC钻头+近钻头工具+Ø172 mm高效螺杆+浮阀+通讯接头+无磁钻铤(MWD随钻测斜仪)+悬挂短节+井下滤网短节+循环阀(多次开关)+Ø127 mm加重钻杆+随钻震击器+Ø127 mm加重钻杆+水力振荡器+Ø127 mm钻杆(水平段后半段)+变扣接头+Ø139.7 mm钻杆(水平段前半段和直井段)。

4 结论

(1)在造斜率较小时，增加造斜率能够显著降低造斜段的接触摩阻总值，同时也能实现全井段的降摩减阻。采用6°/30 m的造斜率相较于4°/30 m的造斜率，造斜段钻柱与井壁间的接触摩阻降低了52.83%，全井段钻柱与井壁间的接触摩阻降低了12.28%。

(2)小尺寸钻杆重量较轻，但在传递较大轴向力时容易发生屈曲变形导致接触摩阻显著上升。在水平段全部采用Ø127 mm钻杆时的接触摩阻相较于全部采用Ø139.7 mm钻杆上升了18.69%。

(3)在水平段采用“大+小”的钻具组合模式，能够有效降低钻柱与井壁间的接触摩阻。在水平段前半段采用Ø139.7 mm钻杆来对抗屈曲变形，在水平段后半段采用Ø127 mm钻杆实现降摩减阻。