双模量梁动力响应的时域GD法求解
黄春林 彭建设
(成都大学机械工程学院 成都 610106)
0 引 言
除了金属材料,工程材料的实际运用中的玻璃钢、塑料、混凝土、橡胶、粉末冶金材料、聚合材料及复合材料等等都具有一定的拉压弹性模量不等的性质.由于双模量材料的大量使用,学者们也对其展开了深入的研究。潘勤学等[1]探讨了不同模量理论广义弹性定律的意义并进行了讨论梳理.对于双模量梁的振动问题,刘相斌等[2]在平截面假定下提出了双模量梁振动过程中中性轴会发生跳变,并分析了双模量弯曲梁的固有频率和主振型.王铭慧等[3-4]在平截面假设下对拉压弹性模量不等材料简支梁的线性振动和非线性振动频率问题进行了研究.杨洋等[5]推导并分析不同模量铁木辛柯梁的自由振动频率特性.吴晓等[6]研究了考虑剪切效应及阻尼时双模量梁的自由振动固有频率问题.但对于双模量梁的受迫振动的时程响应鲜有研究。文中基于双模量理论,运用时域GD法研究均布交变载荷和均布突加载荷作用下简支双模量梁受迫振动的时程响应,讨论了拉压弹性模量不等对受迫振动的影响.
1 GD法简介
GD法(general differential method)是在利用泰勒展开的基础上来使用全域的节点函数值来表示某个基点处的导数值.将某连续函数在基点处做泰勒展开,用全域内节点函数值的加权和来表示基点的导数,从而将微分方程转化为可解的代数方程组,通过求解代数方程组来得到微分方程的解.在域内沿x方向取N个等间距为h节点xi(i=1,2,…,N),设f=f(x)是弹性体内某一连续函数,该函数只随x坐标变化而变化,以起点为基点,其余各点可展开为泰勒级数,则以第i个节点为基点,则任意第n(n≠i)点函数值可以用h表示为
(1)
称fi(i=2,3,…,N-1)为内节点,f1,fN为外边界节点.将各节点(N=1,2,…,i-1,i+1,…,N)整理为如下矩阵.
(2)
式中:
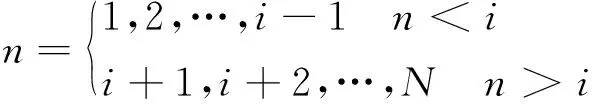
(3)
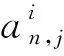
该表达式改写为
Aif=W
(4)
式中:Ai为第i个节点展开的系数矩阵;f为导数矩阵;W为展开点与基点的差值的矩阵.可得到导数矩阵:
f=MiW
(5)
式中:Mi为Ai通过Gauss-Jordan消元法得到的逆矩阵,详细推导过程参见文献[7],由之得到第i个节点的1,2,…,N-1阶导数值.其中第i个节点的k阶导数可表示为
(6)
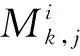
域内不同节点的同阶导数系数列阵可按不同基点展开分别求逆,然后将不同节点的同阶导数整理到一个矩阵C,详细内容参见文献[7].
由之可得任意i节点的k阶导数为
(7)
权系数矩阵C的表达式为
(8)
2 时域GD法解双模量梁的受迫振动问题
2.1 双模量梁的几何关系与本构方程
长度为L、宽为b、高为h,拉伸和压缩弹性模量分别为Et和Ec的矩形截面梁.考虑在线弹性小变形范围内,定义梁的中面层位移为(u,w),则梁的任意纵向截面层距离中面层为y的点的位移为(u′,w′),两者间的几何关系为
(9)
(10)
式中:ρ为梁弯曲变形后中性层的曲率半径.
于是在线弹性范围内,定义双模量梁中性层到几何中面的距离为y0,有
(11)
由材料的本构关系可得
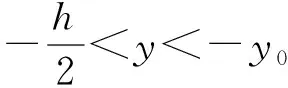
(12)
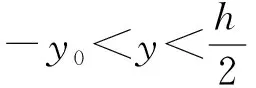
(13)
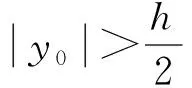
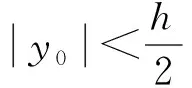
(14)
(15)
将式(12)~(13)代入式(14)~(15)分别可得
(16)
(17)
由式(15)可知,振动过程中即使中性轴位置发生跳变,弯矩M的表达式不变.
结合式(17)可得双模量梁的抗弯刚度为
(18)
设Ec/Et=λ,式(18)可改写为
(19)
当拉压弹性模量相等即λ=1时,式(19)可退化为经典的等模量梁的抗弯刚度.
2.2 双模量梁的振动控制微分方程
设双模量材料的密度为ρ1,则根据达朗贝尔原理,可以得到双模量梁的横向自由振动的控制微分方程:
(19)
式中:w为横向位移;A为横截面积。为方便求解,改写为按位移表达形式后,可得双模量梁的受迫振动控制微分方程.
(20)
式中:(EI)*为梁的抗弯刚度;x为梁沿轴向的自变量;t为时间;w(x,t)为梁的振动小挠度;y0为中性层相对于中面层的距离;ρ1为材料密度;q(x,t)为随时间变化的载荷.
2.3 双模量梁振动微分方程的时域GD法求解
针对均布载荷下梁结构的受迫振动响应问题,运用时域GD法求解此类问题,将该问题的控制方程和边界条件在时间域和空间域都使用GD法离散,得到全域内关于该振动问题的一次线性方程组,在权系数矩阵和广义载荷列阵融入边界条件,使线性方程组可解。通过求解融入边界条件和初始条件的可解一次线性方程组,可得全域内梁振动的位移响应场。
控制方程量纲一的量化,令X=x/L,X∈[0,1],τ=t/T,τ∈[0,1]可得量纲一的量控制方程.
(21)
在空间域取Nx个节点,在时间域内取Nτ个节点并使用GD法离散处理,则有:
(22)
(23)
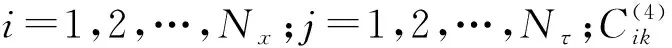
(24)
式中:i=1,2,…,Nx;j=1,2,…,Nτ.
由之可得,在全域内有Nx×Nτ个GD线性方程组,将式(24)改写成矩阵形式,
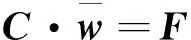
(25)
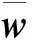
为求解GD线性方程组,需确定定解条件.梁在任意时间节点τj(j=1,2,…,Nτ)都有4个边界条件,在全域内有4Nτ个边界条件,以简支梁为例,其边界条件为
即
(26)
此外,梁在X空间域任意节点Xi(i=1,2,…,Nx)处有两个初始条件,在全域内有2Nx个初始条件,简支梁初始条件为
即
(27)
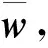
3 算例分析
例1两端简支的梁,长L=50 cm,横截面宽1 cm、高2 cm,质量密度ρ=0.008 kg·cm-3,弹性模量E=15 000 000 N·cm-2,上作用一q=10sin(500t) N·cm-1均布交变载荷.初位移和初速度均为零,求梁中点的位移响应.
例2两端简支双模量梁,其几何参数同例1,拉伸弹性模量Et=15 000 000 N·cm-2,质量密度ρ=0.008 kg·cm-3,在梁上作用一q=10sin(500t) N·cm-1均布交变载荷,初始位移和初始速度均为零,求当压缩与拉伸弹性模量之比Ec/Et=λ分别为0.7,1,2,4时梁中点x=25 cm处的位移响应.
例3两端简支双模量梁,其几何参数同例1,拉伸弹性模量Et=15 000 000 N·cm-2,质量密度ρ=0.008 kg·cm-3,在梁上作用一q=1 N·cm-1突加均布载荷,初始位移和初始速度均为零,求当压缩与拉伸弹性模量之比Ec/Et=λ分别为0.7,1,2,4时双模量梁中点x=25 cm处的位移响应.
三个算例数值结果如下:为说明方法的准确性,针对算例1相同节点用精确解,Newmark-β解和本文的时域GD解列出具体数值见表1,算例1~3对应的图像见图1.

表1 算例1精确解与两种数值解
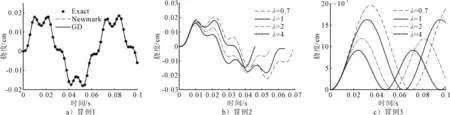
图1 三种方法对比结果
算例1为经典的单模量情况,使用2.3的方法解决问题时,将双模量梁的抗弯刚度(EI)*中λ取为1即可.
求解算例1,当使用时域GD法求解时,在空间域取13个节点,时间域取101个节点,时间步长为0.001 s;使用Newmark-β法求解时,在空间域取13个节点,取时间步长为0.001 s,使Newmark-β法与时域GD法的时间步长相等.由表1和图1a)可知,在相同的时间步长的情况下,时域GD法的解与精确解的误差小于Newmark-β法与精确解的误差.说明时域GD法解决该问题是可行的,所得结果是可信的.
由图1b)可知,λ=1时的结果与经典单模量理论E=15 000 000 N·cm-2时等效;从结果可以看出当λ=0.7时其受迫振动正向幅值相对于λ=1时增大13.5%,负向振动幅值增大22.9%,响应周期增大9.3%;当λ=2时,其受迫振动幅值相对于λ=1时减小但不明显,而响应周期减小14%;当λ=4时,其受迫振动幅值相对于λ=1时减小,其中正向幅值变化不明显,但负向幅值减小21.3%,响应周期减小28%.
由图1c)可知,λ=1时的结果等效于经典单模量理论时弹性模量梁E=15 000 000 N·cm-2的位移响应结果,与λ=0.7时的结果比较,λ=1时振动幅值减小17%,响应周期也减小8.6%;当λ=2时的结果与λ=1时相比,其受迫振动幅值减小27%,响应周期减小15.6%;当λ=4时的结果与λ=1时相比,其受迫振动幅值减小44.7%,响应周期减小25%;.这是由于弹性模量比λ的增大,使得使梁的抗弯刚度增大,最终导致梁的振幅和响应周期减小.
4 结 论
1) 相较于Newmark-β法,时域GD法在时间步长与之相等时,时域GD法与精确解的误差更小.
2) 随着比值λ的增大,中性轴位置偏离几何中面的距离越大,使梁的抗弯刚度得到提升,导致双模量简支梁受迫振动的振幅和响应周期都会相应的减小.而比值λ越大,振幅与响应周期越小.
3) 随对于双模量梁的动力响应问题,若简化为单模量问题计算可能与实际问题产生较大误差,弹性模量比值λ越大,误差越大.

