两个矩阵同时上三角化的充要条件

马文清,张慧婷

(上海师范大学 数理学院，上海 200033)

0 引 言

复矩阵A、B同时上三角化是指存在可逆复矩阵P,使得P-1AP、P-1BP同时为上三角矩阵.复矩阵A、B同时上三角化的充分条件有很多,如两个可交换n阶矩阵A、B可同时上三角化[1];两个矩阵A、B满足rank(AB-BA)≤1时可同时上三角化[1].另外,Levitzki证明幂零矩阵的(乘法)半群可同时上三角化[2],Kolchin证明形式为I+N(N为幂零矩阵)的单幂矩阵半群可同时上三角化[3].

关于充要条件,McCoy证明矩阵A、B同时上三角化等价于h(A,B)(AB-BA)是幂零矩阵,其中h(x,y)是关于x、y的任意非交换单项式[4].但对具体例子来说,验证h(A,B)(AB-BA)是否幂零较复杂,且McCoy提到其等价命题与李代数可解有关[4],但并未给出证明.本文将从线性代数的角度讨论两个复矩阵A、B同时上三角化的两个充分条件，并结合李代数基本理论确定由矩阵A、B生成的gl(n,)的李子代数L=〈A,B〉和导代数中的元素形式,得到矩阵A、B同时上三角化的充要条件为L是可解的.通过证明发现，矩阵A、B同时上三角化等价于p(A,B)(AB-BA)q(A,B)是幂零矩阵，说明h(A,B)(AB-BA)与p(A,B)(AB-BA)q(A,B)的幂零性是等价的,其中p(x,y)、q(x,y)是关于x、y的任意非交换单项式，最后得到两矩阵同时上三角化的一系列等价条件.

1 两个矩阵同时上三角化的充分条件

命题1[1]设A,B∈Mn().若AB-BA=λA,则A、B可同时上三角化.

证明

(Ⅰ)当λ=0时,即AB=BA,则A、B可同时上三角化.

(Ⅱ)当λ≠0时,通过初等变换将AB-BA=λA变为

的形式.

下面证明当A、B满足AB-BA=A时,A、B可同时上三角化.

将v1扩充成n的一组基(v1,v2,…,vn)，使得n=L(v1,v2,…,vn),那么A、B在该组基下对应的矩阵分别为：

其中，μ为B的关于v1的特征值,A1、B1均为n-1阶方阵，且由AB-BA=A得：

从而可得A1B1-B1A1=A1.由归纳可知，A1、B1可同时上三角化，矩阵A、B也可同时上三角化.

若AB-BA的秩满足某些条件,则A、B仍可同时上三角化.

命题2[1]设A,B∈Mn().若rank(AB-BA)≤1,则A、B可同时上三角化.

证明

(Ⅰ)当rank(AB-BA)=0时,该情况归为命题1.

(Ⅱ)当rank(AB-BA)=1时,假设A是在n的标准基下对应矩阵A的线性变换,B是在n的标准基下对应矩阵B的线性变换.任取A的特征值λ,考虑A-λε,则Ker(A-λε)和Im(A-λε)既不为0也不为n.易证Ker(A-λε)与Im(A-λε)是A的不变子空间.

下面证明Ker(A-λε)与Im(A-λε)至少有一个是B的不变子空间.

设[(A-λε)B-B(A-λε)]X=0的解空间为V.

若Ker(A-λε)⊆V:设x∈Ker(A-λε),由[(A-λε)B-B(A-λε)]x=0得(A-λε)(Bx)=0,则Ker(A-λε)是B的不变子空间.

若Ker(A-λε)V:存在x∈Ker(A-λε)但x∉V,令y=[(A-λε)B-B(A-λε)]X,则y是Im([(A-λε)B-B(A-λε)])的基.y=[(A-λε)B-B(A-λε)]x=(A-λε)Bx=(A-λε)(Bx)∈Im(A-λε),则Im(A-λε)是B的不变子空间.

不妨设Im(A-λε)同时是A、B的不变子空间,取Im(A-λε)的一个基扩充为n的一组基,则A、B在该组基下对应的矩阵分别为：

由rank(AB-BA)=1可知:

则rank(AiBi-BiAi)≤1(i=1,2).

由归纳可知,Ai、Bi(i=1,2)可同时上三角化,A、B也可同时上三角化.

通过以上两例研究发现,矩阵A、B同时上三角化蕴含着AB-BA的幂零性,而AB-BA与李代数理论中换位运算的定义有联系[3-4].

下面结合李代数基础理论,探究矩阵同时上三角化的充要条件.

2 两个矩阵同时上三角化的充要条件

2.1 准备知识

定义1[5-6]在复数域上的一个向量空间L中,有一个运算L×L→L,记为(x,y)→[x,y],如果其满足以下公理:

(Ⅰ)[,]运算是双线性的;

(Ⅱ)[x,x]=0对L内所有的x;

(Ⅲ)[x,[y,z]]+[y,[z,x]]+[z,[x,y]]=0(x,y,z∈L).

则称这个运算为x和y的李括号或换位子,L是复数域上的李代数.

定义2[5-6]设L是复数域上的李代数,则由L的换位子[A,B]生成的线性空间也是一个李代数,称为一阶导代数,记为L(1)=[L,L]，那么二阶导代数L(2)=[L(1),L(1)],…,n阶导代数L(n)=[L(n-1),L(n-1)].如果存在整数s,使得L(s)=0,则称L是可解李代数.

定义3[5-6]设L是复数域上的李代数,记Ln=[L,Ln-1]为L的n次幂.如果存在一个有限的整数t使得Lt=0,则称L是幂零李代数.

例1[5-6]由复数域上的严格上三角矩阵组成的李代数记为N(n,),可验证N(n,)是幂零李代数,且它的子代数也是幂零李代数.

命题3[5-6]设L是复数域上的李代数.若L(1)是幂零李代数,则L是可解李代数.

定理1(李定理)[5-6]若复数域上李代数L是gl(n,)的可解李子代数,则n至少包含一个关于L内所有自同态的公共特征向量.

2.2 同时上三角化的充分条件

利用李定理可得到两个矩阵同时上三角化的一个充分条件.

推论1设A,B∈Mn(),记由A、B生成gl(n,)的李子代数为L=〈A,B〉.若L可解,则矩阵A、B可同时上三角化.

证明若L⊆gl(n,)为可解李代数,则由李定理可知A,B∈L存在公共特征向量v1,将v1扩充为n上的一组基(v1,v2,…,vn),由归纳法可知A,B∈L可同时上三角化.

下面回顾一下第1节中矩阵同时上三角化的充分条件,这些条件都是李代数可解这一充分条件的特殊情况:

(a)命题1中由A、B所生成的线性李代数记为L=A⊕B，且满足[A,B]=λA，那么

L(1)=[L,L]=A,L(2)=[L(1),L(1)]=0,

即L可解,故A、B可同时上三角化.

(b)命题2中由A、B所生成的线性李代数记为L，且满足rank([A,B])≤1,那么

L(1)=[L,L]=∑pi(A,B)[A,B]qi(A,B).

因为rank[A,B]≤1,故存在正整数k，使得L(k)=[L(k-1),L(k-1)]=0，即L可解,故A、B可同时上三角化.

关于L=〈A,B〉中任意矩阵同时上三角化的问题,本文有以下推论:

推论2设A1,…,An∈Mn(),L=〈A1,…,An〉(由有限矩阵生成的线性李代数),则A1,…,An可同时上三角化.

例2线性李代数L=A⊕B⊕C且满足[A,B]=C,[B,C]=[A,C]=0.那么,

L(1)=[L,L]=C,L(2)=[L(1),L(1)]=0，

即L可解,故A、B、C可同时上三角化.

2.3 同时上三角化的必要条件

以上证明了矩阵同时上三角化的充分条件是其矩阵生成gl(n,)的李子代数L是可解的.下面我们可以得出此充分条件也是必要条件.

讨论由复矩阵A、B生成的gl(n,)李子代数L=〈A,B〉中元素的形式.

引理1设A,B∈Mn(),考虑gl(n,)的李子代数L=〈A,B〉,且对换位运算满足封闭性,故L中的每个元素可表示为A、B线性组合或∑pi(A,B)[A,B]qi(A,B)的形式.若pi(A,B)=X1X2…Xm,Xj=A，或Bj∈{1,2,…,m},则记pi的次数为m.

证明

L由A、B生成,则其中一定含有A、B线性组合元素.

讨论[Xn[Xn-1…[X2,X1]…]的形式,其中Xi=A或B.若X1=X2,则[X1,X2]=0.考虑X1≠X2的情况,不妨设X1=B,X2=A.

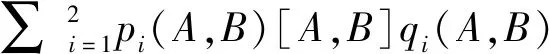
假设[Xn-1[Xn-2[A,B]]]可表示为∑pi(A,B)[A,B]qi(A,B),则

故[Xn[Xn-1[A,B]]]依旧可写成∑pi(A,B)[A,B]qi(A,B)的形式.

因此,由矩阵A、B生成的李代数L中每个元素可表示为A、B的线性组合或∑pi(A,B)[A,B]qi(A,B)的形式.

引理2设A,B∈Mn(),由A、B生成gl(n,)的李子代数记为L=〈A,B〉，那么，L(1)是由形如p(A,B)[A,B]q(A,B)元素张成的线性空间.

证明因为L中元素为∑pi(A,B)[A,B]qi(A,B)或A、B线性组合的形式,故由

得知，L(1)是由形如p(A,B)[A,B]q(A,B)元素张成的.

下面研究矩阵A、B同时上三角化的必要条件,即同时上三角化的矩阵A、B生成gl(n,)的李子代数L,其内部换位子[A,B]=AB-BA生成的一阶导代数L(1)究竟满足什么条件.

命题4设A,B∈Mn(),由A、B生成gl(n,)的李子代数记为L=〈A,B〉.若A、B可同时上三角化,则L(1)为幂零李代数,L为可解李代数.

证明

(a)讨论A、B为上三角矩阵情况.

其中,ai,bi∈,i=1,…,n,则

为严格上三角矩阵.

对p(A,B)[A,B]q(A,B),由A、B为上三角矩阵可得p(A,B)、q(A,B)也是上三角矩阵.又

p(A,B)[A,B]q(A,B)=p(A,B)(AB-BA)q(A,B)=

其中,x1i=a1或b1,i=1,…,m,xni=an或bn,i=1…m;y1j=a1或b1,j=1,…,k,ynj=an或bn,j=1,…,k.

由于ai,bi∈,故

为严格上三角矩阵,则

∑pi(A,B)[A,B]qi(A,B)

也为严格上三角矩阵.

因L(1)是由形如p(A,B)[A,B]q(A,B)的元素张成的,故L(1)中的元素均包含在N(n,)中,而N(n,)是幂零李代数,则L(1)作为N(n,)的子代数是幂零的，由命题3知L是可解的.

(b)讨论一般情况.

若A、B可同时上三角化,则存在可逆矩阵P∈Mn(),使得P-1AP、P-1BP同时为上三角矩阵.记P-1AP=A0,P-1BP=B0,则由情况一得知p(A0,B0)[A0,B0]q(A0,B0)为严格上三角矩阵,记作M.则

p(A,B)[A,B]q(A,B)=P(p(A0,B0)[A0,B0]q(A0,B0))P-1=PMP-1，

其中，M为严格上三角矩阵.因L(1)是由形如p(A,B)[A,B]q(A,B)的元素张成的,故

L(1)={∑PMP-1∣M∈N(n,)}.

定义满足i+k>j时，dij=0的严格上三角矩阵D为k级上三角矩阵,则一般的严格上三角矩阵就是1级上三角矩阵.设M={aij}是k级上三角阵,N={bij}是1级上三角阵,则

当i+k>t,t+1>j时,ait=btj=0,对应的cij必为0,即当i+k+1>j时，cij=0,即k级上三角矩阵与1级上三角矩阵相乘得k+1级上三角矩阵.由于

于是得到如下定理:

定理2设A,B∈Mn(),由A、B生成gl(n,)的李子代数记为L=〈A,B〉.则矩阵A、B同时上三角化的充要条件是李代数L是可解的.

3 两个矩阵同时上三角化的其他充分必要条件

McCoy曾证明两个矩阵同时上三角化的一个等价命题.

定理3[4]两个矩阵A、B同时上三角化的充要条件是对任意的h(A,B),h(A,B)[A,B]是幂零矩阵.

本文证明发现,两个矩阵A、B可同时上三角化当且仅当p(A,B)[A,B]q(A,B)是幂零矩阵,且这两类矩阵的幂零性质是等价的.

命题5对任意h(x,y)、p(x,y)、q(x,y)，h(A,B)[A,B]是幂零矩阵当且仅当p(A,B)[A,B]q(A,B)是幂零矩阵.

证明

若p(A,B)[A,B]q(A,B)是幂零矩阵，易得h(A,B)[A,B]是幂零矩阵.

若任意h(A,B)[A,B]是幂零的,即存在正整数n，使得(q(A,B))p(A,B)[A,B])n=0,则

其中，X=p(A,B),Y=q(A,B),则p(A,B)[A,B]q(A,B)是幂零矩阵.

结合McCoy的结论[4],本文得到两个矩阵同时上三角化的几个等价条件：

推论3设A,B∈Mn(),由A、B生成gl(n,)的李子代数记为L〈A,B〉.则下列命题等价:

(Ⅰ)两个矩阵A、B可同时上三角化;

(Ⅱ)线性李代数L=〈A,B〉是可解的;

(Ⅲ)对任意非交换矩阵单项式h(A,B),h(A,B)[A,B]是幂零矩阵;

(Ⅳ)对任意非交换矩阵单项式p(A,B)、q(A,B),p(A,B)[A,B]q(A,B)是幂零矩阵.