Synchronized perturbation elimination and DOA estimation via signal selection mechanism and parallel deep capsule networks in multipath environment

Ying CHEN, Cong WANG,b,*, Kunli XIONG, Zhito HUANG

a State Key Laboratory of Complex Electromagnetic Environment Effects on Electronics and Information System,National University of Defense Technology, Changsha 410073, China

b Institute of Information Fusion, Naval Aeronautical and Astronautical University, Yantai 264001, China

KEYWORDS Deep capsule network;Direction-Of-Arrival (DOA)estimation;Multipath propagation;Parallel training;Perturbation elimination

Abstract State-of-the-art model-driven Direction-Of-Arrival (DOA) estimation methods for multipath signals face great challenges in practical application because of the dependence on the precise multipath model.In this paper,we introduce a framework,based on deep learning,for synchronizing perturbation auto-elimination with effective DOA estimation in multipath environment.Firstly,a signal selection mechanism is introduced to roughly locate specific signals to spatial subregion via frequency domain filters and compressive sensing-based method.Then,we set the mean of the correlation matrix’s row vectors as the input feature to construct the spatial spectrum by the corresponding single network within the parallel deep capsule networks. The proposed method enhances the generalization capability to untrained scenarios and the adaptability to non-ideal conditions, e.g., lower SNRs, smaller snapshots, unknown reflection coefficients and perturbational steering vectors,which make up for the defects of the previous model-driven methods.Simulations are carried out to demonstrate the superiority of the proposed method.

1. Introduction

Multipath propagation is familiar in low-angle tracking and wireless communication. The multipath components can lead to the distortion of the physical characteristics of direct signal,which may result in significant decline of the Direction-Of-Arrival(DOA)estimation precision.Meanwhile,it is too complicated to accurately model the reflectance characteristics of complex reflectors in practical application.Therefore,we need to find a DOA estimation method with satisfactory adaptation to the complex multipath environment.

Spatial Smoothing (SS)-based algorithms and Compressive Sensing (CS)-based algorithms have already been applied for DOA estimation of multipath signals.1-13However, the application of spatial smoothing implies array aperture reduction,which leads to resolution capability degradation.1,2CS-based methods can achieve better performance without aperture loss under the condition of low SNR and small snapshots.4-13Nevertheless, all these methods require precise modeling of the array output, which is much more difficult to satisfy in practical systems. Especially, in complex topography, such as rugged ground surface and rough sea surface,the steering vectors of the multipath signals will suffer perturbation caused by the irregular reflectors.14-17Various calibration methods are proposed to seek for precision improvement. For instance, in Ref.14, the sparse Bayesian learning based method is adopted to estimate the perturbation parameters and the DOAs of the direct and multipath signals iteratively.Likewise,these calibration methods are also based on accurate prior knowledge of the multipath model. Thus, the above model-driven methods will suffer significant performance degradation in practical application.

Deep Learning (DL) is emerging as a powerful technique for array signal processing,benefiting from its enhanced modeling capability.18-20DL-based DOA estimation strategies have attracted extensive attention.21-26In Ref.21, a multitask autoencoder and a series of parallel multilayer classifiers are introduced to reconstruct spatial spectrum with satisfying imperfection adaptation. In Ref.23, DL is integrated into the massive Multiple-Input Multiple-Output (MIMO) system as an end-to-end method for super-resolution DOA estimation.In Ref.25, Wu et al. proposed an efficient deep convolution network-based spatial spectra recovery algorithm for DOA estimation. Simulation results have demonstrated their superior performance over model-driven methods and previous machine learning-based methods. Nevertheless, in general,the networks need to be trained in advance.Only if the practice circumstances are equal to the one in the training,will the estimation performance of the DL-based method be the best. As shown in previous studies, the single network is normally trained for specific circumstance. For adapting to various circumstances,simply widening the kind of samples may result in heavy computations and difficult convergence of the single network. Thus, only using single network for DOA estimation rarely satisfies the actual needs and is extremely limited in practice.

Motivated by these DL-based methods and taking into consideration the limitations of DL, we take advantage of the powerful modeling capability of DL to solve DOA estimation problem in multipath environment and adopt signal selection mechanism to target specific source in focus area for single network within parallel networks. In this paper, first, a signal selection mechanism is introduced to roughly locate specific signals, with particular frequency,to spatial subregion via frequency domain filters and CS-based method. Then, the corresponding single network, within the parallel deep capsule networks, is used to estimate the spatial spectrum. The final directions of the signals are obtained based on the spectrum via amplitude interpolation.Major contributions of this paper are as follows:

(1) A DL-based method is proposed for DOA estimation in face of multipath phenomenon induced by complex reflectors. The perturbation effect can be autoeliminated during the end-to-end DOA estimation process. This method is data-driven and does not rely on accurate perturbational multipath signal model, so as to make up for the drawbacks of previous modeldriven methods.

(2) The signal selection mechanism separates different kinds of sources to the corresponding single networks for parallel processing.This processing contributes to the practical application of the single network that is fitter to target only a few specific sources.Training sets of different subregions are used to train the corresponding parts of parallel networks,which can make the whole training much easier and faster.

(3) Considering that the rank of the correlation matrix is 1,we set the mean of its row vectors as the input of the corresponding single network within the parallel deep capsule networks.Compared with the existing input feature extraction strategies of DL-based methods, this process effectively reduces the dimension of input without sacrificing information.

(4) The capsules are integrated into networks to comprehend the relationship between part and whole and capture more hierarchical structure information of the spectra,which effectively enhances the learning capacity of networks compared with the conventional Deep Convolution Networks (DCN).

(5) Amplitude interpolation is adopted to achieve better precision of DOA estimation. This strategy can break the limit that the estimates of the source locations have been confined to grids by the proposed DL-based estimation process.

The rest of this paper is outlined as follows: Section 2 formulates the perturbational multipath signal model. Section 3 presents the proposed DOA estimation framework. Section 4 analyses the Cramer-Rao bound of model-based methods.Section 5 is about simulations and analyses to show the superior performance of the proposed method. Conclusions are drawn in Section 6.

Notations: Vectors are denoted by boldface small letters,while matrices are denoted by boldface capital letters. vec（•）denotes vectorization operator. ⊗represents the Kronecker product. ⊙denotes Hadamard product.

2. Problem formulation

According to Fresnel reflecting area,array antennas in various heights receive the multipath signals from different regions and are affected by different perturbation, and thus the complex fading coefficients distributed to different antennas are no longer the same. A typical perturbational multipath model is showed in Fig.1.Assume that K narrowband far-field sources S（t）=［s1（t），s2（t），•••，sK（t）］Timpinge on an N-element Uniform Linear Array (ULA) from directions θ1，θ2，•••，θK.Thereinto, each source signal produces L multipath components via different routes. The multipath components of sk（t）impinge on the array from direction angles βk1，βk2，•••，βkL.Thus, the array output can be written as

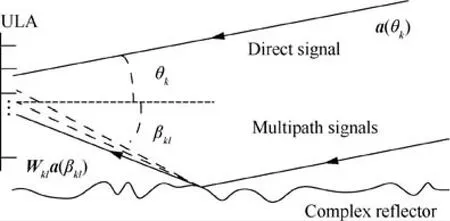
Fig. 1 Perturbational multipath signal model.

Though the perturbation of steering vectors of multipath signals caused by complex terrain is considered in the model above,it is only denoted by mathematical perspectives approximately, which deviates far away from actual condition. The mismatched modeling may pose significant negative influence on the performance of model-based methods based on SS technique and CS technique in practical application. DL-based methods do not rely on precise modeling,and thus we consider achieving perturbation elimination and DOA estimation via the following proposed DL-based framework.

3. Proposed approach

In this paper, we propose a framework, consisting of a signal selection mechanism and a group of parallel DOA estimation networks, to address the DOA estimation problem in multipath environment. As shown in Fig. 2, the proposed method is composed of three main steps:(A)signal selection;(B)input feature extraction; (C) parallel networks based DOA estimation. The detailed steps are as follows:

(1) Frequency selection.This step emphasizes signals in particular frequency points.

(2) Spatial subregion determination. This step provides an approximate knowledge of the locations to determine the space subregions of sources.

(3) Input feature extraction. This step constructs an input feature,with lower dimension,to facilitate the proposed deep capsule network designing and training, thereby integrating DL into super-resolution DOA estimation of direct and multipath signals.

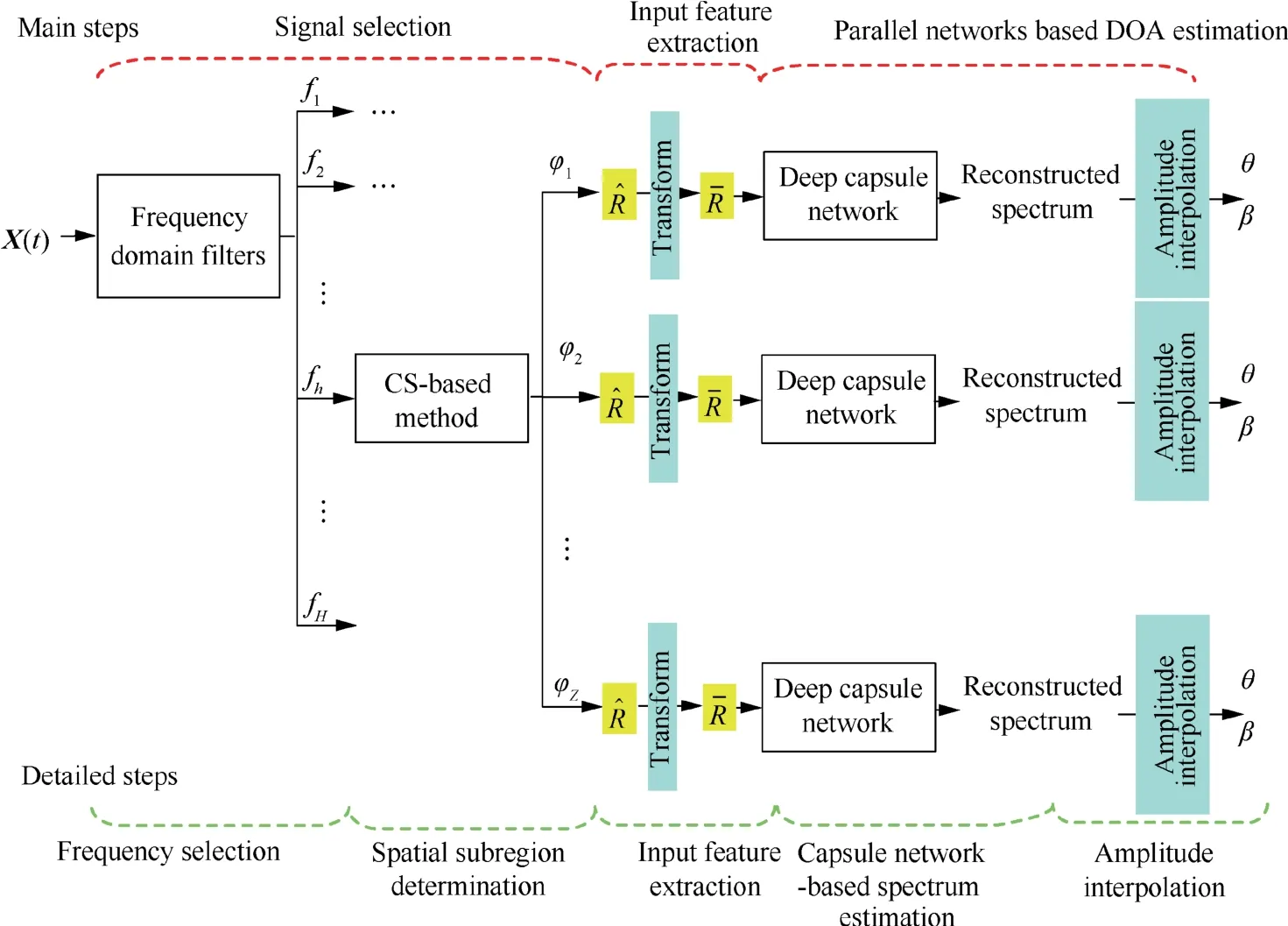
Fig. 2 Proposed perturbation elimination and DOA estimation framework.

(4) Capsule network based perturbation elimination and spectrum estimation.In this step,the designed deep capsule network has learned the mapping relationship between the input feature,containing the information of perturbation, and the super-resolution spectrum, and thus the perturbation effect can be auto-eliminated during the end-to-end spectrum estimation process.

(5) Amplitude interpolation.In this step,better precision of DOA is achieved by carrying on amplitude interpolation around the locations of the spectrum peaks.

In conclusion,the signal selection mechanism has separated different kinds of sources, and input feature extraction has facilitated the later networks designing and training, while the parallel DOA estimation networks have synchronized perturbation auto-elimination with effective spectrum estimation.

3.1. Signal selection

In signal selection mechanism,firstly,frequency domain filters are used to emphasize signals in several particular frequency points, i.e., f1，f2，•••，fH， meanwhile significantly reducing noise. Then, the CS-based method is adopted to provide a rough estimation of the target’s DOA under fh，which can separate the target signal from its multipath components and identify the location subregion with only small number of snapshots. Finally, the selected signals will be sent to the corresponding single networks.

By appropriately selecting various coefficients, a frequency selection filter can be designed so that signals with frequency components in certain frequency bands will pass while signals contained in frequency components in other frequency bands will be attenuated.The linear time invariant system will change the input signal spectrum S（ω ） according to its frequency response H（ω ）,and produce an output signal with a spectrum of Y（ω ）=H（ω ）S（ω ）. In a sense, H（ω ） acts as a weighting function or a spectrum shaping function for different frequency components in the input signals.

In CS-based method, with the establishment of the spatial overcomplete form model, the DOA estimation problem becomes the reconstruction of the spatial spectrum.4-8The number of signal is smaller than the number of special grids,and thus the overcomplete array output has great sparsity.In general, the objective function is defined as

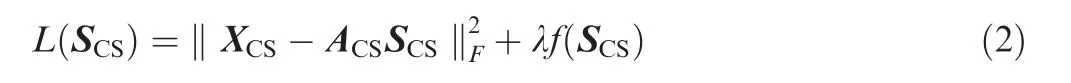
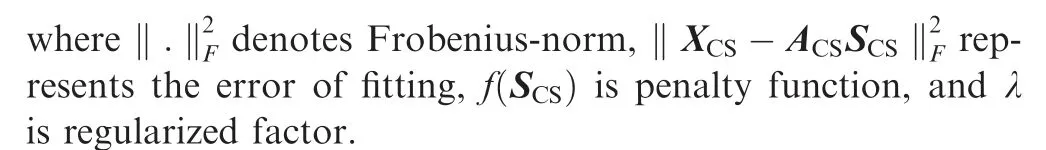
For low-angle targets,we suppose that the array is very far from the sources.14-16The multipath signals may impinge onto the ULA from the angle region under the normal of array,and the angle of the direct signal may be approximately equal to the angle of the multipath signal. Thus, as shown in Fig. 3,we consider decomposing the potential direction space, under the specific fh, into Z subregions that are symmetrical about the normal of array, i.e., ［φ1，φ2，•••，φZ］.

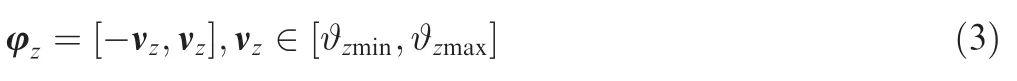
where νzis the zth angle set. There are overlapping clusters between adjacent subregions for completeness of all cases.

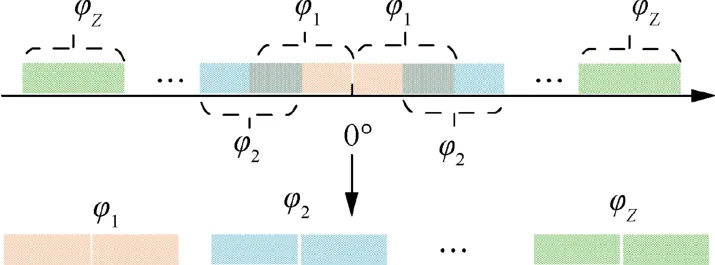
Fig. 3 Spacial division.

3.2. Feature extraction

After signal selection, we preprocess the array output to construct the input feature of the deep capsule network designed for the corresponding subregion.

where ΔR is the estimation error of R,and Rn1，n2represents the element of the covariance matrix, n1，n2=1，2，•••，N.satisfies the conjugate symmetry.

where real（•）and imag（•）represent the real and image parts of the complex-valued entity. R～is normalized by its norm in favor of activating neurons. The preprocessing process of the input feature is summarized in Algorithm 1.

Algorithm 1. Input preprocessing Input:X 1. ^R ←1G XXH covariance matrix in Eq.(5)2. for n ∈［1，N］ iterations do sum the row vectors together 3. R～n ←R～n-1+ ^Rn 4. end for 5. R～←N R～N calculate the average Eq.(6)6. R-←RealvaluedTransform（real（R～/norm（R～）），imag（R～/norm（R～）））return R-1

3.3. Parallel networks based perturbation elimination and DOA estimation

We note that the DL-based method will suffer heavy computations and difficult convergence when the kind of samples increases. Moreover, only if the practice circumstances are equal to the one in the training will the estimation performance of the DL-based method be the best.Thus, the single network is fitter for targeting only a few specific sources in focus areas.

Considering above application limitation of the single network and the unknown gain and phase perturbation caused by multipath signals on each antenna, we adopt parallel deep capsule networks to eliminate the perturbation effects and recover spectrum by learning the mapping from R-to the super-resolution spectrum P. Capsule structure can capture the hierarchical structure of the specific type of entities and learn the relationships between part and whole,27-29benefiting from which the attitude information of spectra can be preserved.Hence,the new-added capsule structure will contribute to better generalization of network in untrained scenarios,such as lower SNR,smaller snapshots,and unknown complex reflection coefficient.

Different from the original deep capsule networks in Refs.27-29,we introduce the capsule architecture into 1D application and adjust the parameters of the capsule layers to suit the perturbation elimination and DOA estimation problem that we are dealing with. The 1D networks can learn the correlation of adjacent features, and the size of kernels determine the length of adjacent features that will be learned by 1D networks. In Fig. 4(a), as for the proposed deep capsule network framework, two 1D convolutional layers, with 25, 1×3 convolution kernels and 16, 1×5 convolution kernels respectively, are used to extract initial feature maps which serve as the inputs to the primary capsules.In the primary capsule layer(a convolutional capsule layer),there are 4 channels of convolutional 4D capsules. In the digit capsule layer (contains 11 capsules),each 8D digit capsule receives input from all the primary capsules below. At the end of the architecture, a fullconnected layer is added to construct the spectrum.

A capsule is defined as a vector that consists of a group of neurons,whose parameters can represent various properties of a specific type of entity. Consider that viis the output of a lower level capsule. The input ζ to the higher-level capsule can be calculated as follows:

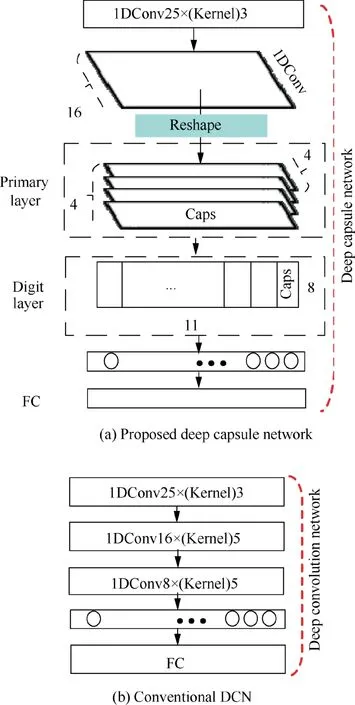
Fig. 4 Architecture of neural network.

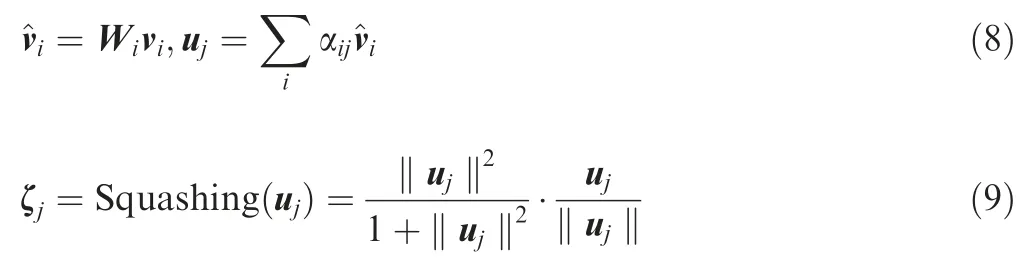
where Wiis weight matrix, and Squashing（•） is an activation function that can realize normalization of vectors. Ifconforms to the actual output of the higher level capsule,the coupling coefficient αijdetermined by the dynamic routing process will increase. Dynamic routing can be deemed as a parallel attention mechanism that allows each capsule at higher level layer to pay attention to some capsules at layer below and to neglect others.We have rsumroutings between the primary capsule layer and the digit capsule layer.The agreement for updating αijis calculated as follows:

Algorithm 2. Routing process Input:^vi =Wivi 1. capsule i in layer L and capsule j in layer L+1:ηi ←0 2. for r iterations do 3. capsule i: α ←softmax（η） Eq.(11)4. capsule j: uj ←∑iαij^vi Eq.(8)5. capsule j: ζj ←Squashing（uj） Eq.(9)6. capsule i and j: ηr i ←ηr-1i +^vriζj Eq.(10)return ζ

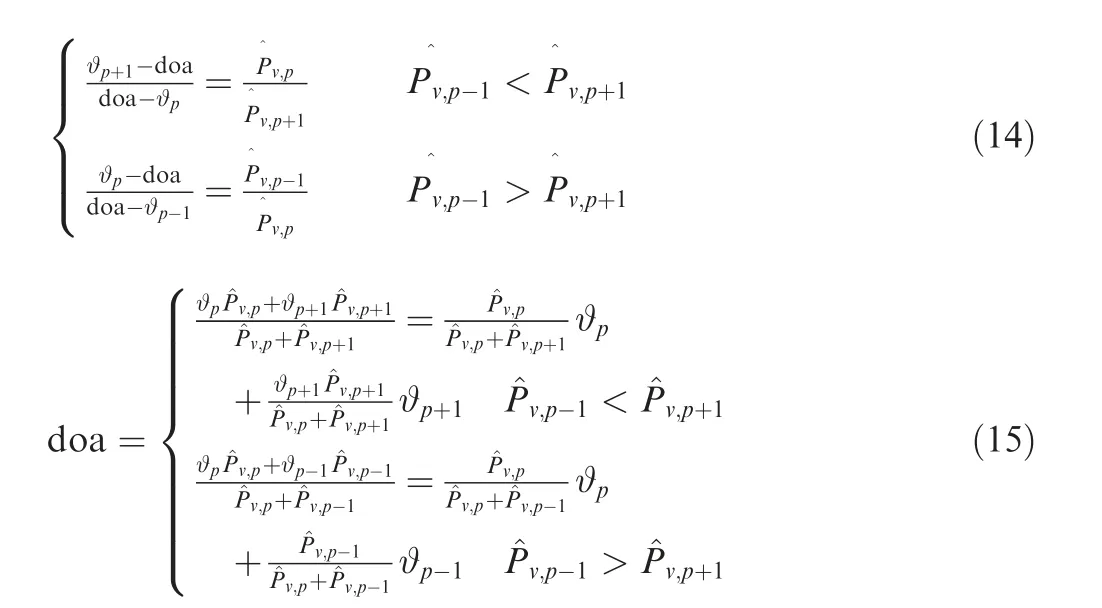
where ϑpis the angle corresponding to the spectrum peak,ϑp-1and ϑp+1are the adjacent angles of ϑp,v，pis the amplitude of the spectrum peak,andv，p-1andv，p+1,corresponding to ϑp-1and ϑp+1, are the adjacent amplitudes ofv，p.

3.4. Summary of proposed method

The process of the proposed method is summarized as shown in Fig. 5:

(1) Training part: Firstly, we classify the training data into several groups according to frequency division and space division. Then, we preprocess the array output in data set to construct the input feature of the network.Finally,features of different groups are sent to different deep capsule networks for parallel training.

(2) Test part:Firstly,specific signals are selected and rough located by frequency domain filters and CS-based method. Secondly, we preprocess the array output to construct the input feature of the deep capsule network designed for the corresponding subregion under specific frequency.Then,the spectrum is estimated by the corresponding deep capsule network. Finally, the final directions of the signals are obtained based on the spectrum via amplitude interpolation.

4. Cramer-Rao bound analysis

Cramer-Rao Bound(CRB)is the lower bound for an unbiased estimator under white Gaussian noise assumption.17As for model-based method, we divide the multipath signal model into the following two categories according to the priori information.

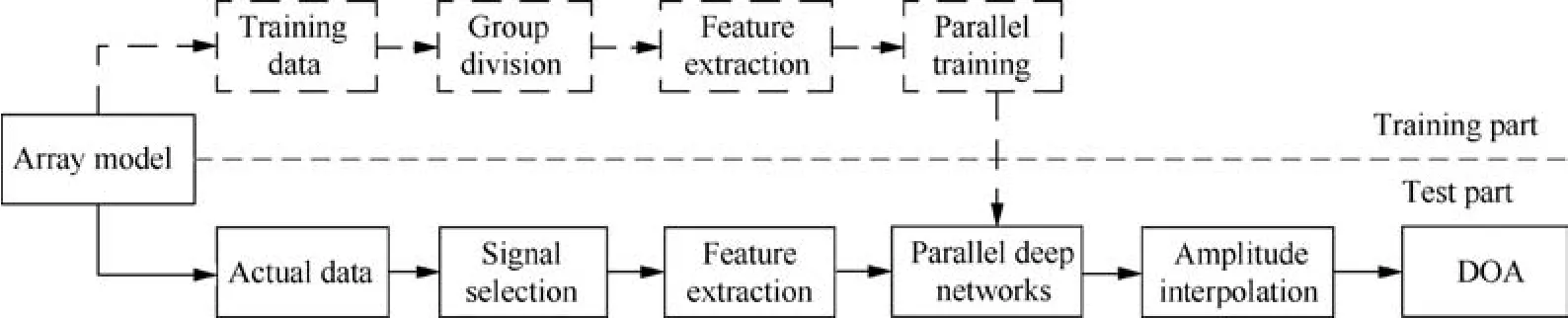
Fig. 5 Process of proposed method.

5. Simulations and analysis

This section carries out simulations to show the predominance of the proposed input feature over state-of-the-art input features in terms of training performance and computational complexity, the predominance of the proposed method over the conventional DCN-based DOA estimation method in generalization, and also its predominance over the most common SS-MUSIC method in complex reflector adaptation.

5.1. Simulation setting and network training

We use the largely simplified perturbational multipath signal model in Fig.1 to facilitate simulations in this paper.The simplification is reasonable for performance comparison. That is because, compared with model-driven methods, the proposed learning-based method does not make use of any prior information about perturbational steering vectors.Training dataset is generated by simulations. In this paper, as for every single network, the dataset is collected in two-signal scenario, i.e.,one specific direct signal and one main multipath component,to simplify the simulation calculation.Directions of more multipath components can also be estimated based on much more powerful computing capability.

Consider a ULA consisting of 15 physical antenna sensors.The unit spacing d is chosen to be half wavelength.Covariance matrices are obtained from 128 snapshots. We sample the space of interest,［-21°，21°］,using 1°intervals to form 43 spectrum grid units. The subregions are

Take subregion φ1as an example.Angular separation set is｛0°，1°，•••，10°｝.For each angular separation Δθ,the direction of the direct signal is generated from ［-5°+Δθ，5°］ with a 1°interval,while the direction of the multipath signal is generated from［-5°，5°-Δθ］with a 1°interval.The SNR set of both signals is ［5，10］dB with 1dB interval. The reflection coefficient is 0.95exp（jπ）. The perturbation parameter on the nth element is defined as

where ηa～U（-0.2，0.2）, ηp～U（-20°，20°）. The train frequency is set at 200 MHz. 300 groups of snapshots are collected for each setting. Finally, as for a single network, a total of 16500 vectors are collected in the sample dataset.

Our implementation is based on Keras,which employs Tensorflow on its backend.The experiment platform is an Ubuntu server with NVIDIA GTX 2080 Ti graphics cards. The training process is off-line and parallel. Each single network is trained for 400 epochs with a minibatch size of 128 and finetuned by using the ADAM optimizer with a learning rate of 0.001. The sample set is shuffled in each epoch. In order to illustrate the excellent performance of the proposed framework, the DCN shown in Fig. 4(b) is also trained in the same condition for comparison. We randomly set aside 20% of training samples as the validation set,which is used to evaluate the model after each epoch.

In the proposed method, the routing number is a vital parameter for determining whether the capsules can obtain the best coupling coefficients. In order to select an optimal routing number, we set the routing number to［1，2，3，5，7，10，20，30，50］ for comparison. As shown in Fig. 6,the proposed network with 3 iterations of routing optimizes the MSE faster and converges to a lower MSE at the end. In theory, the MSEs will decrease as the number of routing increases. However, in the simulation, we have the following findings:

(1) Although, within a certain range of routing numbers,the lower MSEs may be achieved with the increase of routing number rsum, there is an optimal fitting when rsum=3.

(2) When the number of routing iteration is too large, e.g.,rsum=20，30，40，50，the MSE curves will show a trend of fluctuating downward, which may aggravate with the increase of routing number. What’s more, the MSEs show significant increases when rsumchanges from 30 to 50.All of these are because too large number of routing could easily lead to missing the optimal coupling coefficients during training process. The imperfect coupling coefficients may cause the increase of the MSEs even significant degradation of the whole MSE performance.

(3) As shown in Fig.6 and Table 1,the MSEs under 3 routing iterations are comparable to the MSEs under 30 routings iterations, but with much less training time and faster convergence.

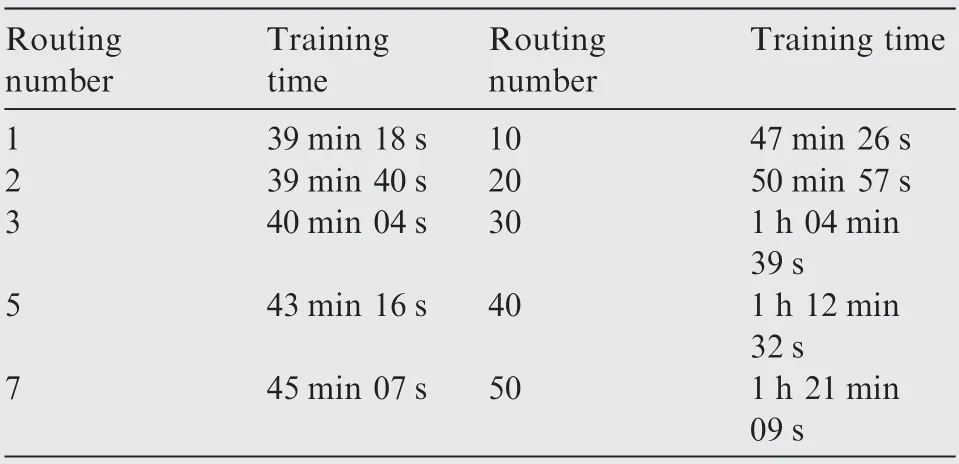
Table 1 Train time versus routing iteration number.

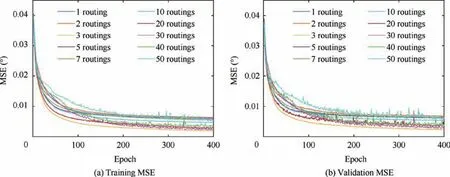
Fig. 6 Training and validation loss versus different routing iteration numbers.

Comprehensively, we have adopted 3 routing iterations in the later simulations, considering the purpose of balancing MSEs and training time.

5.2. Comparison of training performance and computational complexity

In this subsection, we investigate the superiority of the proposed input feature in terms of training performance and computational complexity by comparing it with the commonly used input features, and the effectiveness of the convolutional capsule architecture in terms of learning ability promotion by comparing it with the conventional DCN.

We compare the proposed input with other feasible or presently used ones, e.g.,

(2) beamform-based low-resolution spectrum:

The MSEs versus epochs are shown in Fig.7.To assess the computational complexity of network with different input features, we record the number of trainable parameters (space complexity) and the training time needs (time complexity)for every case in Table 2.

The results show that the training and validation MSEs of the proposed input feature are comparable to those of Ref.21,but the former has much few parameters to train and takes much less time for training. This indicates that the proposed preprocessing effectively lessens the complexity of the network and the difficulty of training but maintains a satisfactory performance. The reason is that the proposed preprocessing method has achieved dimension reduction of the input feature without information sacrifice. What’s more, the proposed feature provides lower MSEs throughout the whole training procedure than the others except the input feature in Ref.21.Compared with the conventional DCN,the capsule-based network has more parameters to train because of the capsule structure and takes longer to train because of routing process,but with lower MSEs,which benefits from its ability of capturing more hierarchical structure information of the spectra.

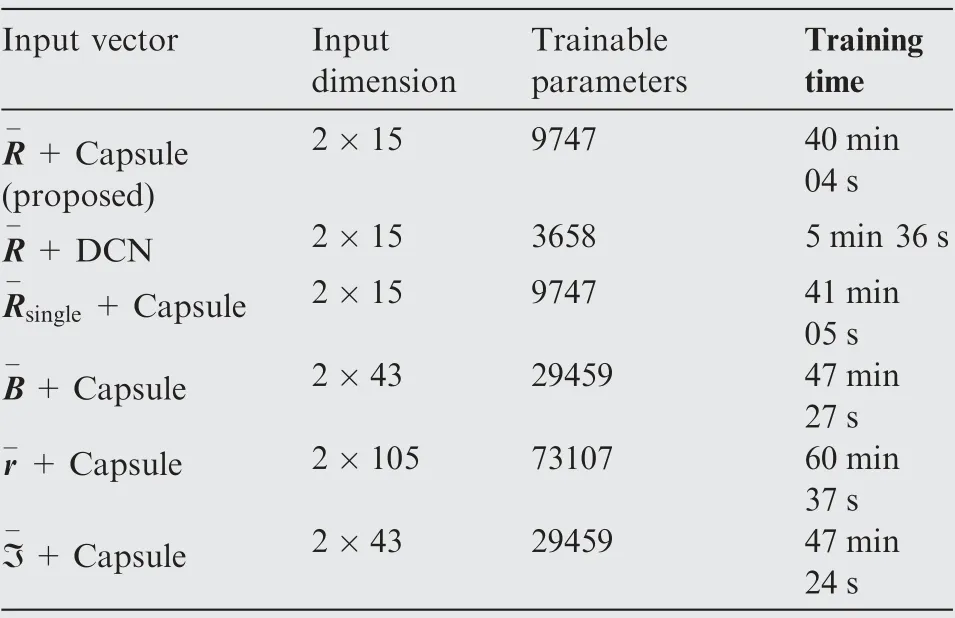
Table 2 Complexity and averaged training time.

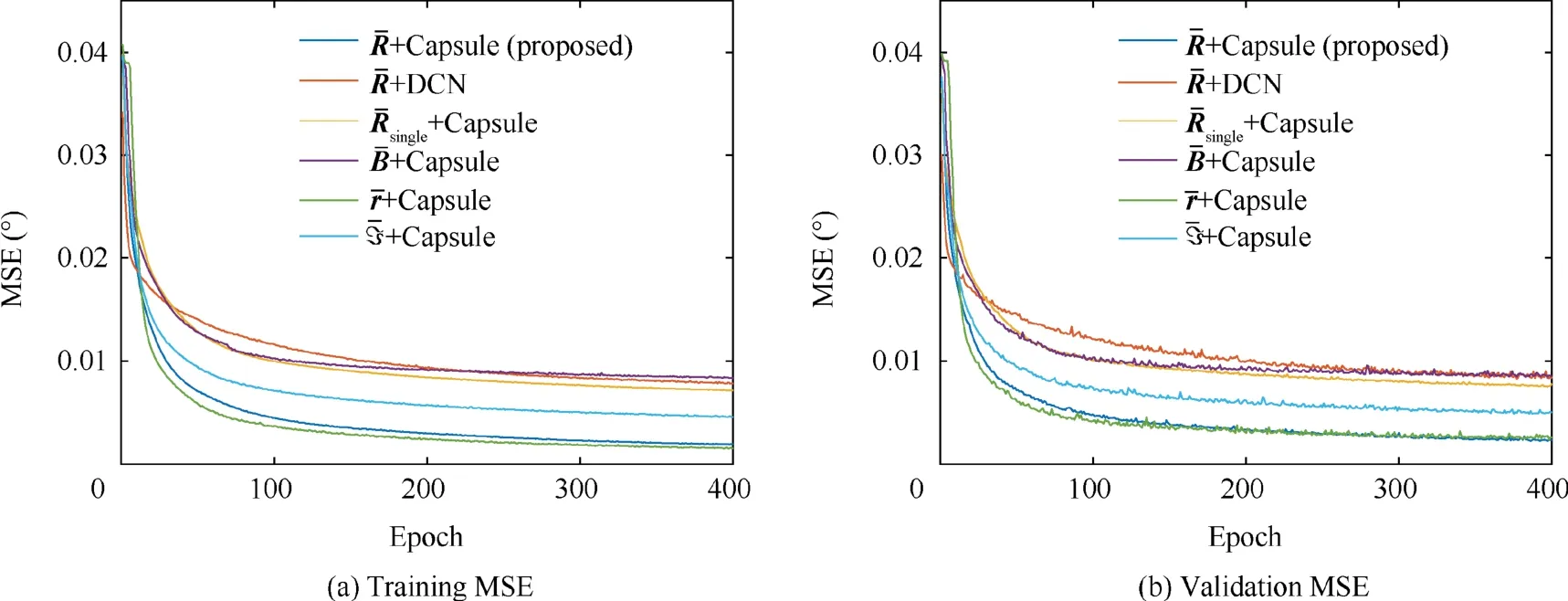
Fig. 7 Training and validation loss of different methods.

5.3. Untrained scenarios generalization

In this subsection, we show the estimation performance of the proposed method in untrained scenarios and compare it with the conventional DCN method.

Assume that the direction of the direct signal uniformly varies from 1.5°to 4.5°(off the presumed grid and uncontained in the training set), and the direction of the multipath signal uniformly varies from-1.5°to-4.5°(off the presumed grid and uncontained in the training set).The SNR is 5dB,and the frequency is set at 200 MHz. We consider two reflectors with reflection coefficients of 0.55exp（jπ） and 0.95exp（jπ/3） (different from the training scene), respectively.As shown in Fig. 8, the DOA estimations of the proposed method match the true values better than the conventional DCN method.

Assume that the directions of the direct and multipath signals are 4.25°and -3.25°(off the presumed grid and uncontained in the training set), respectively. First, we fix the snapshots number at 128. The Root Mean Squared Error(RMSE)that can be used to evaluate the DOA estimation precision of different methods is defined as

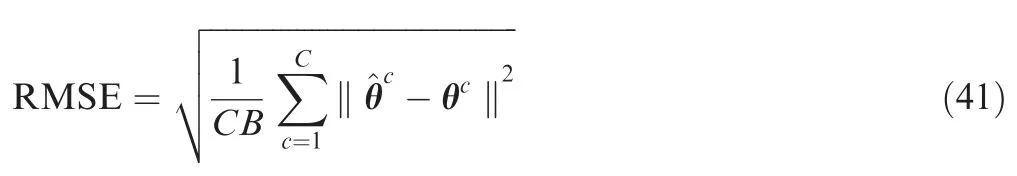
where C refers to the number of the Monte-Carlo trials, B denotes the number of signals,and θcandare the true direction set and the estimation results in the cth test, respectively.The RMSEs of these two methods,with respect to varying signal SNR, are shown in Fig. 9(a). Then, we fix the SNRs at 0dB. The RMSEs of these two methods, with respect to varying snapshot, are shown in Fig. 9(b). Finally, two 0dB signals with a set of angular distances ［2°，3°，•••，9°］are assumed to impinge onto the array simultaneously. The signal directions are -4.25°+ φ and -4.25°+ φ + Δφ with φ ～U（-0.5°，0.5°）. The RMSEs of these two methods,with respect to varying angle separations, are shown in Fig. 9(c). Each RMSE is evaluated by averaging 500 ensembles, and the frequency of each signal is set at 200 MHz. It may be observed that the proposed method shows much better generalization performance under untrained small snapshots scenarios and low-SNR scenarios. Since the grid is set to 1°in this paper,the meaningful minimum value of the angle separation is 2°. As shown in Fig. 9(c), the average RMSEs of these two methods can all be kept within 1°, but the superresolution capability of the proposed method is better.

As shown above, the capsules effectively promote the generalization of the neural network. This proves that the activation function Squashing（•） and the dynamic routing of the capsules accelerate the activation of neurons and enhance the modeling capability of the network.

5.4. Complex reflector adaptation

In this subsection,we carry out simulations to demonstrate the adaptation of the proposed method to multipath scenarios caused by complex reflectors. The existing conventional model-driven methods that deal with DOA estimation for multipath signals have almost the same precision in the presence of complex topography, while the optimized methods that are proposed to solve complex reflection problems are usually designed for specific and simplified multipath models. Thus,we chose the baseline method, i.e. SS-MUSIC, to carry out contrast experiments.

Direct and reflected signals are assumed to impinge onto the array from directions of 3.25°and -2.25°(off the presumed grid and uncontained in the training set). The SNR of each signal is fixed at 10dB,and the frequency of each signalissetat200 MHz.ηa～U（-0.1ρ，0.1ρ）,ηp～U（-10°ρ，10°ρ）, ρ ∈［0，5］ adjusts the strength of roughness of the reflector.The RMSEs with respect to varying ρ are shown in Fig. 10. Each RMSE is evaluated by averaging 400 ensembles.

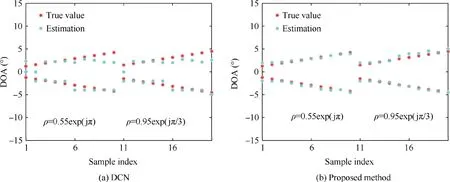
Fig. 8 DOA estimation under untrained reflection coefficient.

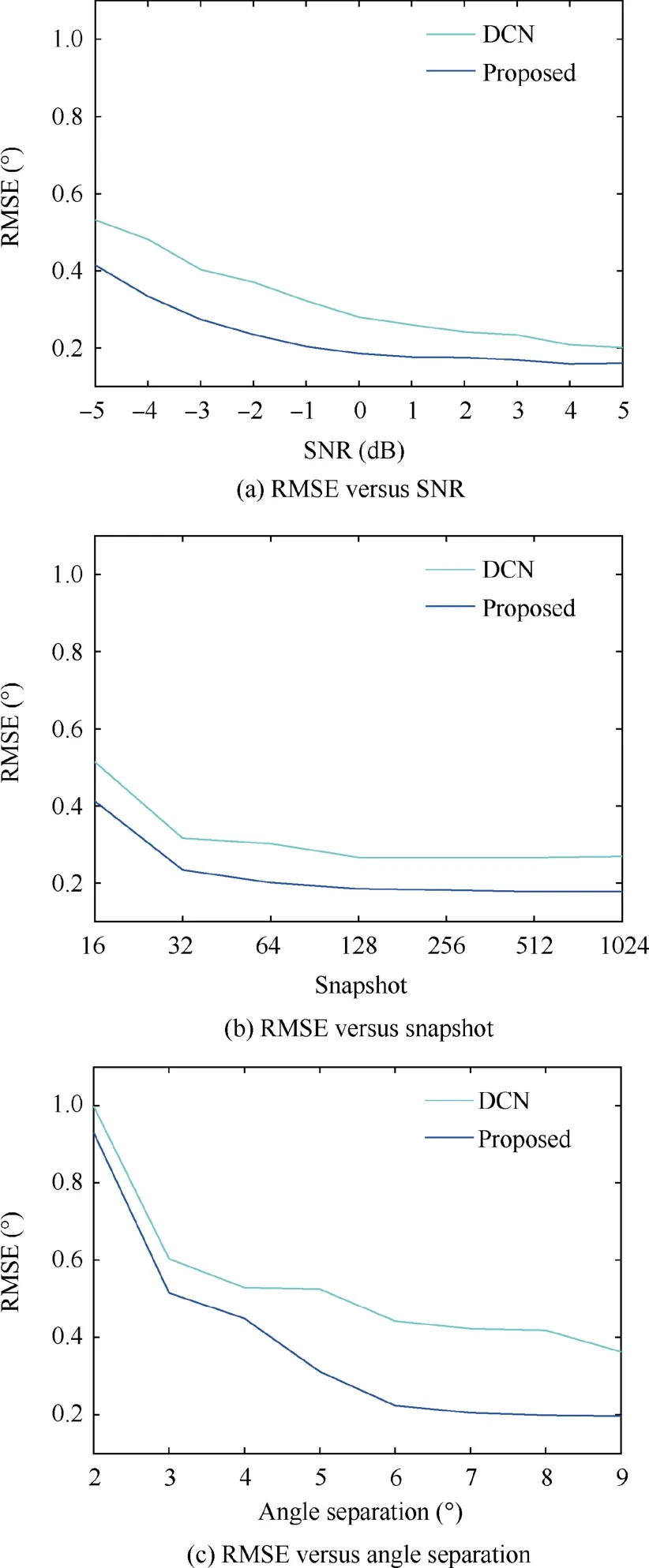
Fig. 9 RMSE performance of DOA estimation.

In Fig.10,as ρ becomes larger,DOA estimation RMSEs of the SS-MUSIC algorithm increase obviously,while the estimation precision of the proposed method seldom changes. It is because that the proposed method can derive a direct mapping from R-to super-resolution spectrum, avoiding the mathematical perspectives approximately with various additional assumptions. The perturbation effects have been autoeliminated during the end-to-end spectrum estimation process.However, the SS-MUSIC algorithm relies heavily on the precise prior information of the signal model, and thus the mismatch modeling has resulted in its serious performance deterioration. When ρ=0, the SS-MUSIC is a little worse than the proposed method because its search interval is set to 0.1°.

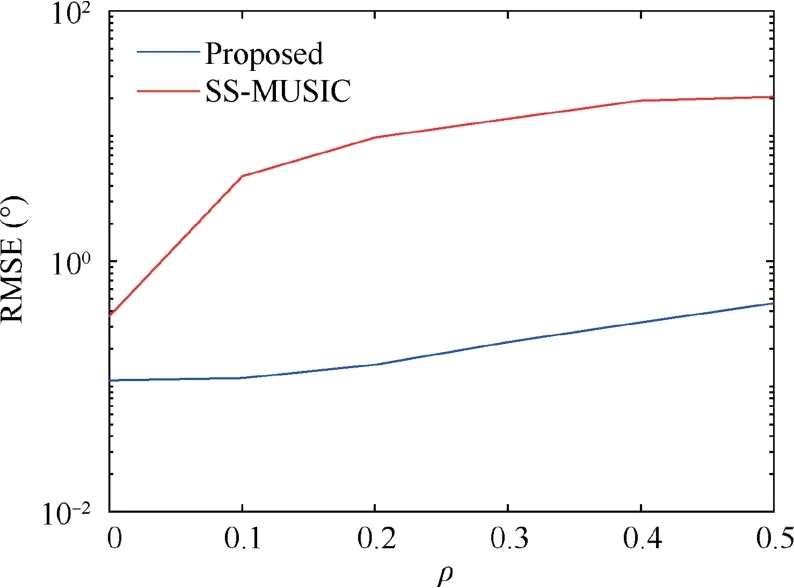
Fig. 10 Performance comparison under different strength of roughness.

Assume that the direction of the direct signal is from 1°+Δφ，2°+Δφ，3°+Δφ，4°+Δφ，5°+Δφ［］,

Δφ ～U -0.25°，0.25°（）. The multipath signal is approximated as its corresponding mirrored version. SNR is 0dB. The proposed method, just like Model I, does not take advantage of the prior information of the model. As shown in Fig. 11,however, its RMSE curve is lower than the CRB I curve,and gradually close to the valley value of the CRB I curve with the increase of the elevation angle, i.e. the angle of the direct signal. Model II contains more prior information, and any accurate prior information is important to improve the performance of CRB, hence its CRB curve is much lower than the RMSE curve of the proposed method.Meanwhile,the estimation precision of the proposed method is also limited by the size of the spatial grid and untrained perturbation from complex reflectors.In order to narrow the gap between the RMSE curve of the proposed method and the CRB II, we can try to more fully mine the prior information (e.g., prior information of signal,prior information of array structure)contained in the array direction finding model,and incorporate the prior information in network design.

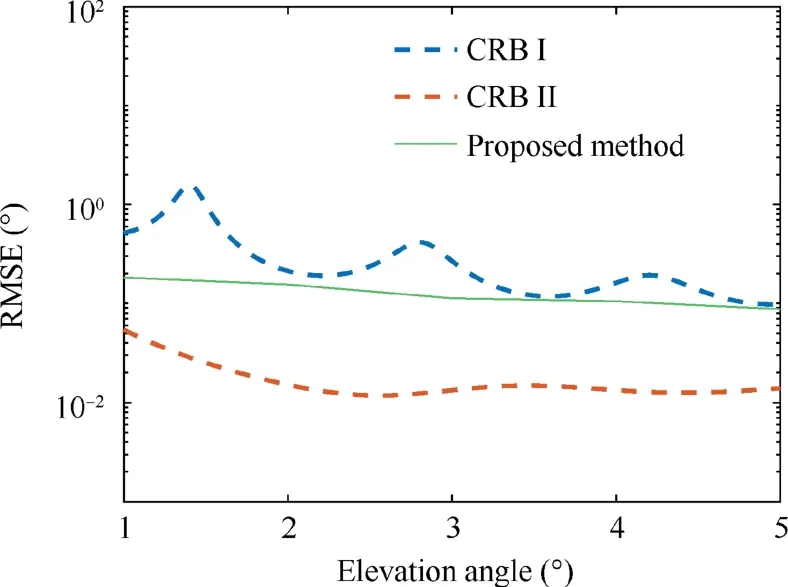
Fig. 11 RMSE versus elevation angle.

Despite its advantage, the proposed method also has obvious limitation.As for the single network,the dataset for training is generated only in two-signal scenarios, i.e., one specific direct signal and one multipath component, which does not match with the reality. The single network will show the best performance only if under the circumstances with the same number of multipath components as the training,but the conventional model-driven methods, e.g., SS-MUSIC, could not be limited by fixed number of signals. Therefore, to deal with more multipath components by single networks, except enhancing the computing capability of devices, we are exploring a novel strategy for separating each signal, not just each kind of signal, before DL-based DOA estimation, then estimating each signal respectively.

6. Conclusions

In this paper, we introduce a framework based on the deep capsule network for perturbation auto-elimination and effective DOA estimation for specific sources under multipath situations. Firstly, a signal selection mechanism is introduced to roughly locate specific signals to spatial subregion via frequency domain filters and CS-based method. Then, the corresponding single network, within the parallel deep capsule networks,is used to construct the spatial spectrum. After simulation verification, the following conclusions and expectations can be drawn:

(1) A DL-based method is proposed for DOA estimation in face of multipath phenomenon induced by complex reflectors. The perturbation effect can be autoeliminated during the end-to-end DOA estimation process. The results of the simulation prove that the proposed method provides more superior perturbation adaptation compared with the previous parametric methods.

(2) Compared with the existing input feature extraction strategies of DL-based methods, the proposed preprocessing process effectively reduces the dimension of input without sacrificing information. The simulation results have verified the superiority of the proposed input feature over the previous ones in terms of training performance.

(3) The capsules have effectively enhanced the learning capacity of networks. The simulation results have verified the superiority of the capsule-based method over the previous DCN-based method in terms of generalization.

(4) Amplitude interpolation has provided more precise DOA estimation for sources with directions off the presumed grids.

(5) The signal selection mechanism can separate different kinds of sources to the corresponding single networks for parallel processing.Nevertheless,the number of multipath components that the single network could deal with depends on the one in the training.On the contrary,the conventional model-driven methods could not be limited by fixed number of signals. Thus, faced with the limitation of the proposed method,except enhancing the computing capability of devices for dealing with more multipath components by single networks, we are exploring a novel strategy for separating each signal,not just each kind of signal,before DL-based DOA estimation, and then estimating each signal respectively.

Declaration of Competing Interest

The authors declare that they have no known competing financial interests or personal relationships that could have appeared to influence the work reported in this paper.

Acknowledgement

This work was supported by the Program for Innovative Research Groups of the Hunan Provincial Natural Science Foundation of China (No. 2019JJ10004).