Parameters for evaluating the efficiency of inlet compression

Keting CHEN, Lianjie YUE,*, Xinyu ZHANG

a State Key Laboratory of High Temperature Gas Dynamics, Institute of Mechanics, Chinese Academy of Sciences, Beijing 100190, China

b School of Engineering and Science, University of Chinese Academy of Science, Beijing 100049, China

Keywords Airbreathing engine;Compression efficiency;Compression quality;Inlet;Self-consistency

Abstract The efficiency parameters are studied in this paper for evaluating the compression quality of the inlets with different compression degrees and assessing different design methods. Selfconsistency is proposed for the efficiency parameters, based on two mathematically derived efficiency parameters, entropy rise coefficient and compression quality efficiency. Two efficiency parameters are then examined for equal intensity shocks system to show their capabilities in characterizing the quality of compression system with different compression degrees, and representing the average compression efficiency of the entire inlet. And the process efficiency and compression quality efficiency are compared in the Mollier diagram to afford a clear understanding of their difference in evaluating the overall and the local compression efficiency.

1. Introduction

As a component of the airbreathing engine,the inlet is responsible for capturing and compressing freestream air to supply a flow with suitable temperature, pressure, and mass flow rate for efficient operation of engine. Hence, the inlet is a critical component which affects significantly the overall cycle efficiency of the entire engine,especially the ramjet and the scramjet engine.

A variety of efficiency parameters have been introduced to describe the efficiency of the inlet compression process. These efficiency parameters are divided into two classes.1Class 1 includes parameters that implicitly define the entropy rise associated with the compression process, regardless of the amount of compression,while Class 2 is composed of those parameters that relate the entropy rise to the compression degree.

The total pressure recovery is universally accepted as a meaningful measure of the performance for subsonic and supersonic aircraft engine inlets,2,3which indicates the final thrust potential of the air flow. The total pressure recovery belongs to Class 1 mentioned above,and an abundance of theoretical and experimental works has been done to describe its behavior.4-14Other similar parameters can be expressed as functions of the total pressure recovery and the incoming flow conditions, including adiabatic kinetic energy efficiency, static pressure efficiency, and dimensionless entropy rise, and they also belong to Class 1.1,15,16

Nomenclature cpspecific heat at constant pressure Esentropy rise coefficient hspecific enthalpy pstatic pressure Rgas constant sspecific entropy Tstatic temperature γspecific heat capacity εccompression efficiency ηBBillig’s compression efficiency ηcadiabatic compression process efficiency ηlcompression quality efficiency πcstatic pressure ratio σtotal pressure recovery ψcstatic temperature ratio Subscripts 0entrance of inlet 3exit of inlet xstarting point of isentropic compression process

However,higher compression degree for inlet design generally leads to lower total pressure recovery.17,18Thus, the total pressure recovery and other efficiency parameters in Class 1 cannot comprehensively evaluate the inlet compression efficiency on their own.Parameters in Class 2,such as thermodynamic efficiency, adiabatic compression process efficiency,Billig’s compression efficiency, and entropy rise efficiency,1,15,16can be expressed via total pressure recovery and static pressure ratio under the hypothesis of a calorically perfect gas, and they may have more valuable implications than parameters in Class 1.

An issue is raised as to how to compare the compression quality of the inlets with different compression degrees or how to evaluate different design methods (they generally generate inlets with different pressure ratios). Obviously, the parameters in Class 1 can only be used to compare the inlet compression quality with the same compression degree. For the inlets with different amount of compression, it is unclear whether the parameters in Class 2 can be directly used as the indicators even though they reflect the flow loss coupled with compression ratio.Hereafter,the heat loss during the compression process is not taken into account, that is to say, the inlet compression is assumed to be adiabatic.

2. Mathematical derivation of efficiency parameters with selfconsistency

Essentially, we need to compare the compression quality of different inlets at a unified scale. We thus need to find an inlet compression efficiency parameter in Class 2,which can characterize the quality of the compression process, while remaining independent of the compression degree. It ought to be an invariant in the evaluation of overall compression and local compression for an equal intensity shocks system, e.g., it should meet the self-consistency requirement.

Suppose a specific inlet is made up of a series of child compression processes,which have the same compression efficiency εc,the overall compression efficiency of the inlet should also be εcaccording to the physical description of the self-consistency requirement. It must be a function of entropy rise and static pressure ratio. Thus the total pressure recovery can be expressed as a function of the efficiency εcand the static pressure ratio, and thus the total pressure recovery of the whole inlet can be written in the form of

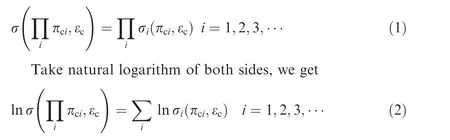
where i denotes the ith child compression process.

Now convert the static pressure ratio, one of the independent variables in Eq. (2),to a logarithmic form,and the equation can thus be rewritten as

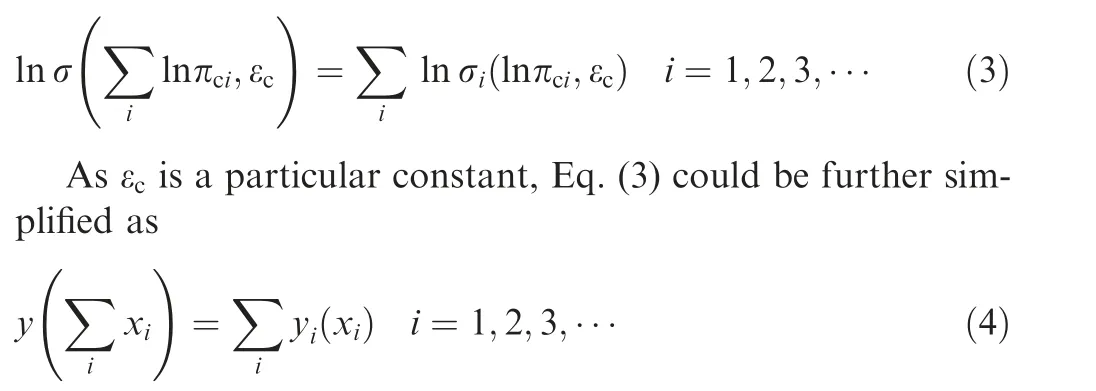
where y=ln σ，x=ln πc.

Intuitively, a linear mapping, y（x ）=L•x, where L represents a linear operator,can appropriately describe the relation of x to y.For the sake of simplicity and without loss of generality, the linear mapping can be defined as a direct proportional function, denoted as

The two efficiency parameters could also be applied to the general inlet compression processes to evaluate the flow loss caused by the shocks and the boundary layer. Although the same compression efficiency for each child compression in the inlet are not realized in the practical inlet design, the two efficiency parameters mentioned above can be regarded as the indicators of the average compression efficiency for all micro-compression processes of the entire inlet.

3. Discussion on compression efficiencies for shock systems

3.1. Efficiencies for an equal intensity shocks system

An equal intensity shocks system is introduced to facilitate discussions on the self-consistency of the above two parameters.The system is composed of several discrete oblique shocks with the same intensity (i.e., the normal Mach number is the same for all shocks).3,19,20In fact, most of inlets are designed approximately as an equal intensity shocks system.As the static pressure ratio and the total pressure recovery are identical across each shock, each compression process via the shock has the same compression quality. Denote the static pressure ratio and the entropy rise of each shock in equal intensity shocks system asπc0and Δs0. When an incoming flow passes through these equal intensity shocks successively, its static pressure ratio, entropy rise and efficiency parameters relative to its initial state are shown in Table 1.

The static pressure ratio grows exponentially while the entropy rise is proportional to shock numbers. The entropy rise coefficient and the compression quality efficiency can be found to be invariants, i.e., equal to those of a single shock.Billig’s compression efficiency11and the adiabatic compression process efficiency,1also called process efficiency,are calculated for comparison and listed in Table 1. For a calorically perfect gas,these two efficiency parameters can be expressed as a function of the total pressure recovery and the static pressure ratio

The expressions in Table 1 are the transformations of Eq. (9) and Eq. (10). It is apparent that Billig’s compression efficiency and the process efficiency are not invariants for the equal intensity shocks system, that is, they cannot selfconsistently reflect the overall and local compression efficiency,though they take into account the effect of static pressure ratio.As a matter of fact,they concerns more about the overall compression efficiency of the inlet. Similarly, other efficiency parameters in Class 2,such as thermodynamic efficiency,have the same self-consistency problem.

3.2. Comparison of efficiency parameters for different compression systems

In order to check the compression efficiencies of different compression systems at Mach number 6.0, three equal-intensityshock systems have been taken as examples. In the equalintensity-shock system,the total pressure recovery and the static pressure ratio across each shock are identical (i.e., the normal Mach number is the same for all shocks). As shown in Fig. 1, there are three shocks with the first ramp angle of 7in Case 1, and five shocks with the first ramp angle of 7in Case 3. Case 2 includes five shocks with the first ramp angle of 8.

It can be noted in Table 2 that three compression systems have different pressure ratios and different total pressure recoveries. In general, higher pressure ratio results in larger total pressure loss.It is difficult to judge the compression quality by examining the indicator of total pressure recovery alone.As efficiency parameters in Class 2,both the process efficiency and the compression quality efficiency relate the total pressure loss to the static pressure ratio. Compared to Case 1, the process efficiency of Case 2 is higher. Nevertheless the compres-sion quality efficiency exhibits an opposite trend. Apparently,the compression quality of the shock system in Case 2 should be admittedly poorer because the total pressure loss in Case 2 is larger for each shock. So we can argue that the process efficiency cannot evaluate the compression quality of the inlets with different compression degrees.

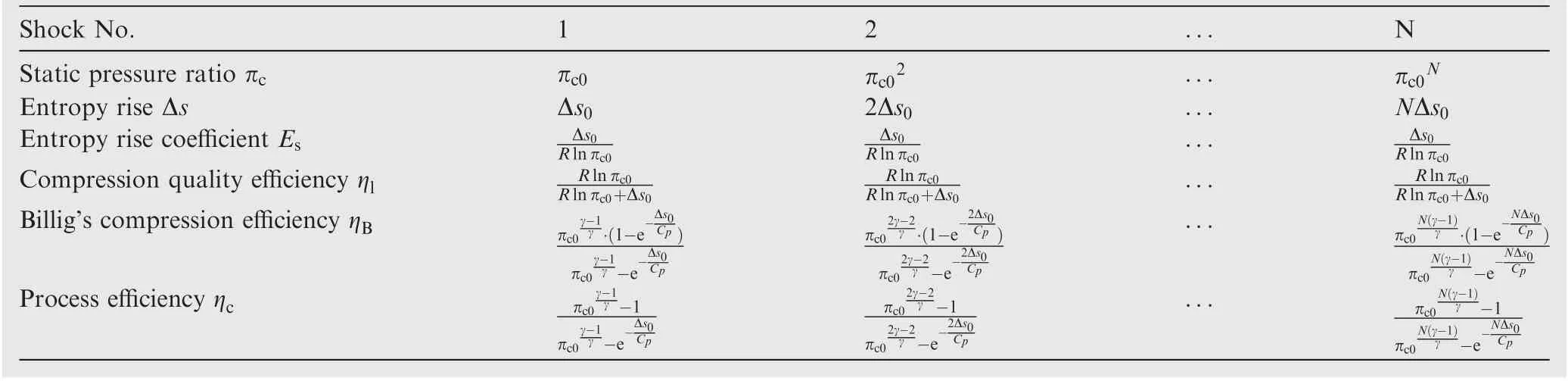
Table 1 Properties of the flow after i equal intensity shocks.

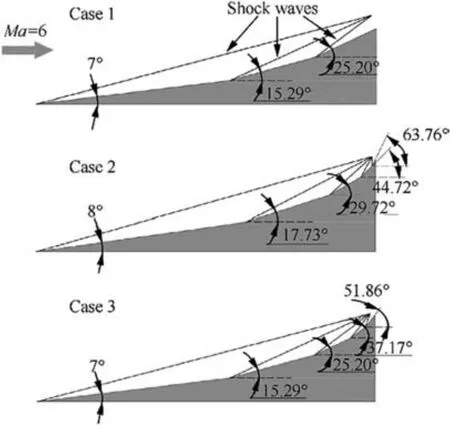
Fig. 1 Diagrams of equal-intensity-shock systems.

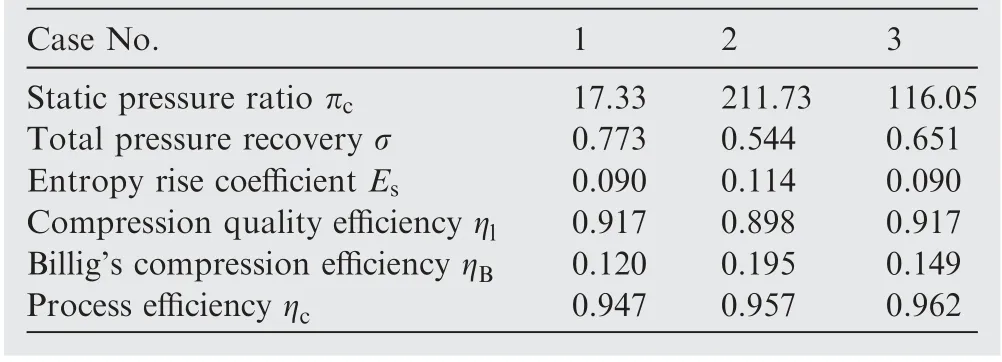
Table 2 Performance of different compression systems.

As to Case 1 and Case 3, the flow compression is designed with the same quality because each shock is characterized by the same pressure ratio and entropy rise. The compression quality efficiency reveals this characteristic, while the process efficiency has different values because of the self-consistency problem.And Billig’s compression efficiency,listed in Table 2,also has the problems as the process efficiency does. Thus,these two efficiency parameters may be unfit for comparing the quality of compression processes of the inlets with different compression degrees.They reflect the compression efficiency of the entire inlet.

4. Mechanism of self-consistency for compression quality efficiency

It has been proven in mathematics that both the compression quality efficiency and the entropy rise coefficient can selfconsistently reflect the overall and the local compression efficiency of the inlet. But the adiabatic compression process efficiency doesn’t possess this property.In this section,the Mollier diagram of the inlet compression process is taken into account to elucidate the mechanism.

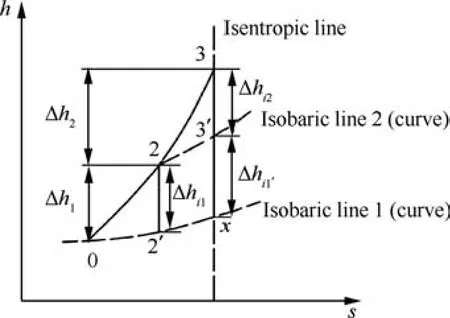
Fig. 2 Mollier diagram of process efficiency.

Let us first analyze the process efficiency. As shown in Fig. 2, assume that the compression process 0-2 has the same process efficiency value as the compression process 2-3.According to the definition of the process efficiency,1

In other words, Δhi1′>Δhi1, that is, the longitudinal spacing between the two isobaric lines in Fig. 2 will continue to expand with the increase of entropy. Thus, the process efficiency of the whole inlet is

For the isentropic compression process from Point x to Point 3, the static pressure ratio can be expressed as

By substituting Eq.(18)into Eq.(17),a new formula of the compression quality efficiency for compression process 0-3 could be obtained as

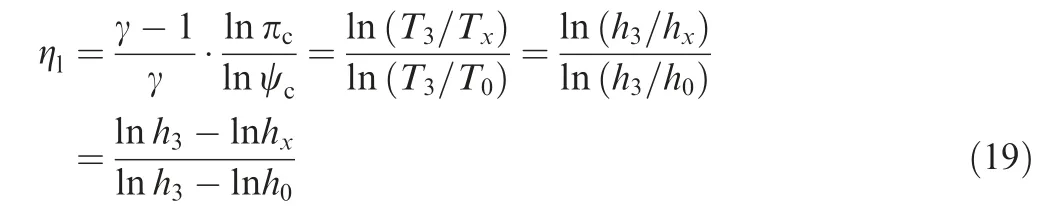
In Fig. 3, the longitudinal coordinate is ln h according to Eq. (19). Assume that the compression process 0-2 and the compression process 2-3 have the same compression quality efficiency, that is

Eq.(23)proves that the compression quality efficiency meets the self-consistency requirement. Intuitively, it is because the definition formula of the compression quality efficiency in Eq.(19)takes the logarithmic form of static enthalpy compared to process efficiency, which turns the isobaric lines into straight lines in the new Mollier diagram.This comparison facilitates a clearer understanding of the two efficiency parameters.

5. Conclusions

The inlet is a critical component of an airbreathing engine,and a lot of efficiency parameters have been defined to evaluate its compression efficiency. The parameters are studied in this paper for evaluating the compression quality of the inlets with different compression degrees. In order to measure the inlet compression quality at a unified scale, the property of selfconsistency is demanded for efficiency parameters,which characterize the inlet compression quality independent of the compression degree.

Two new efficiency parameters, compression quality efficiency and entropy rise coefficient,are derived mathematically to represent the average compression efficiency of the entire inlet. By comparison with adiabatic compression process efficiency for an equal intensity shocks system, they have been proven capable of characterizing the quality of compression system, while the process efficiency is unfit for evaluating the compression quality of the inlets with different compression degrees, though it reflects the flow loss coupled with compression ratio. Furthermore, the process efficiency and the compression quality efficiency are analyzed in the Mollier diagram to elucidate the mechanism of their difference. It is revealed that the self-consistency of the compression quality efficiency results essentially from taking the logarithm form of static enthalpy in its definition formula,which turns the isobaric lines into straight lines in the new Mollier diagram.

Acknowledgments

This work was supported by National Natural Science Foundation of China (Nos. 11672309 and 11472279).