非线性空气舵系统模态试验及颤振设计研究
杨鑫鑫,徐春铃,韩 旭,王捷冰,刘晓华
(空间物理重点实验室,北京,100076)
0 引 言
颤振是在大气环境中飞行的飞行器在结构弹性力、惯性力、气动力耦合作用下发生的振动发散现象。飞行器的翼舵结构由于存在较大气动力作用,且结构刚度较弹身偏弱,是颤振设计的主要关注对象。工程实践中由于公差和加工偏差、安装偏差的存在,在连接环节较多的舵系统结构中不可避免地存在间隙、摩擦等非线性因素,导致非线性的结构动特性,进而影响空气舵的颤振特性。
赵永辉等[1]研究了具有操纵面间隙的三自由度二元翼段的气动弹性响应;李道春等[2]通过Henon方法准确定位间隙非线性刚度转折点,完成了二元机翼气弹响应分析;谷迎松等[3]研究了带迟滞非线性环节的二元机翼的气动弹性响应;以上研究工作基于二元机翼,无法直接应用于三维真实结构。杨宁等[4]采用子结构法研究了具有间隙的多自由度折叠翼的颤振特性,但与舵系统的间隙形式有较大差异。黄程德等[5]采用虚拟质量法对间隙进行建模,完成了全动舵的CFD/CSD耦合颤振分析,但实际结构虚拟质量法的参数如何确定未进行说明。本文从当前的工程设计出发,对某全动舵的模态试验数据表现出的非线性特点进行总结,进而采用颤振分析商用软件ZAERO完成舵系统的颤振分析,对当前工程设计中的非线性颤振设计进行说明和总结。
1 模态试验
试验对象为安装在舱体上的某空气舵系统,包括舵面、舵轴、轴承、摇臂等传动结构、伺服舵机。
模态试验采用步进正弦方法,测得结构的频响函数,再由多参考点最小二乘复频域算法(PloyMax)获取结构的模态参数。
步进正弦方法是通过控制激振器将在一定频率范围内分段变化频率的激励施加到试验件上,同时使用加速度传感器测量试验件的响应,当激励力稳定后,采集激励力和响应的时域信号,经过信号处理得到频域的激励F(ω)和响应X(ω),再计算出频响函数:

再由多参考点最小二乘复频域算法(PloyMax)分析频响函数,得到模态参数。
1.1 试验设备及系统
模态试验设备配置包括模态试验控制采集系统、激振系统和加速度测量系统等,加速度数据采集由模态试验控制采集系统进行,模态参数识别由LMS公司模态试验系统进行。常温模态试验使用仪器设备见表1。
步进正弦方法的试验设备和软件系统由控制采集处理系统、响应测量系统和激振器激振系统组成,如图1所示。
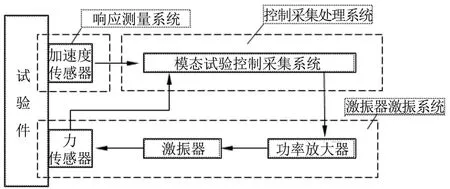
图1 步进正弦法的测试系统示意Fig.1 Schematic Diagram of Test System
1.2 模态试验结果
舵系统模态试验获得的频率随舵面负载和激振力幅值的变化如表2所示。其中一阶振型为扭转,二阶振型为弯曲,如图2所示。
由模态数据可见:
a)随着负载的增加,一阶和二阶频率均单调增高,主要是由于舵面负载给舵系统施加了一定附加刚度,同时减小了舵系统间隙的影响。
b)随着激振力幅值的变大,一阶扭转频率和二阶弯曲频率均有降低的趋势。这主要是由于激振力增大后克服了摩擦力,间隙得到释放,导致间隙对频率的影响进一步放大。
c)由于间隙、摩擦等非线性因素的存在,舵系统模态特性随着舵面负载和激振力幅值的改变而明显改变,为后续颤振分析带来了不确定性。
d)激振力增加到80 N时,除50 kg负载一阶模态频率变化为9%,其他模态频率的变化均在3%以内,认为随着激振力增大模态频率已趋于收敛。而随着负载增加,一、二阶频率差变大。认为表中所列数据已经包含了一、二阶频率最接近的工况,可以以此为输入进行颤振分析。
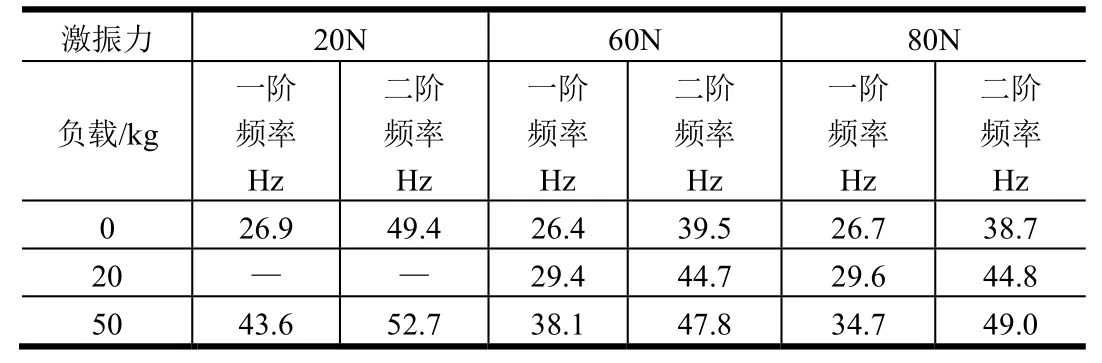
表2 模态试验频率Tab.2 Modal Frequency from Test
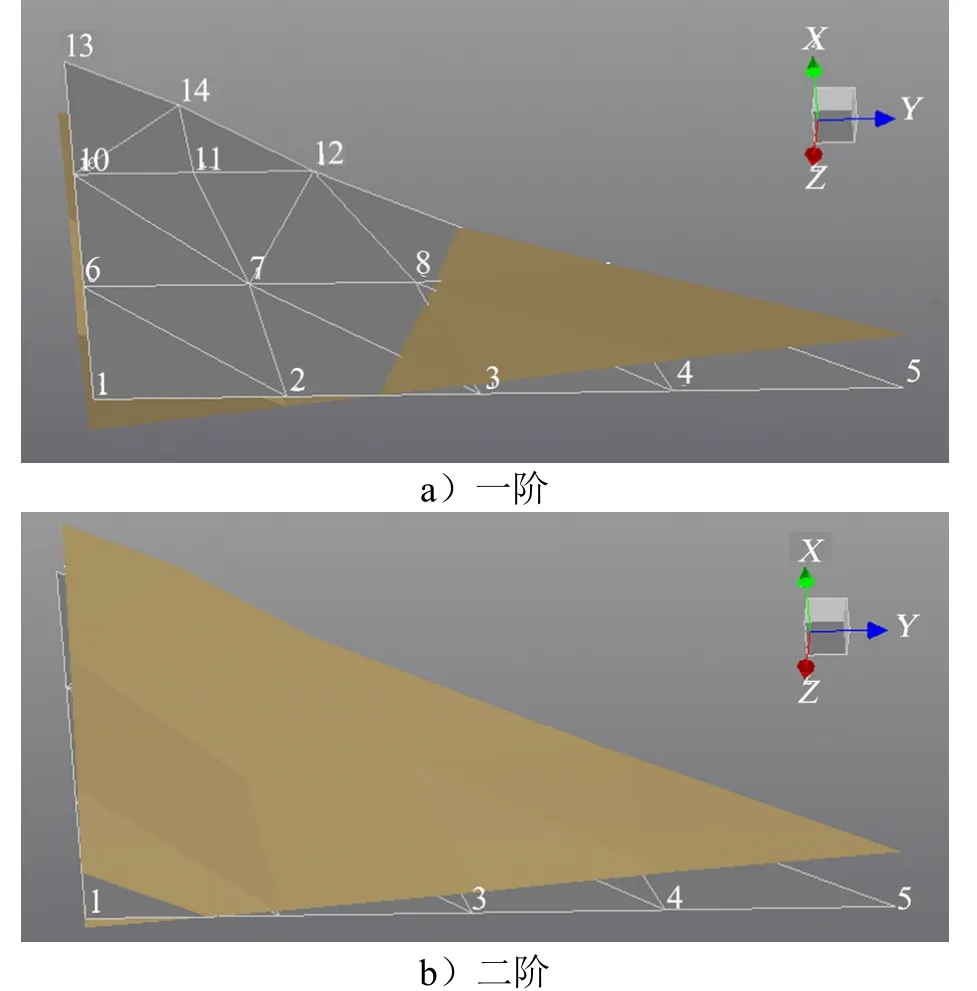
图2 舵面振型示意Fig.2 Modal Shape of Mode 1
2 颤振分析
2.1 颤振动力学方程
以模态试验得到的舵系统固有模态频率、振型、广义质量为输入,通过拉格朗日方程建立空气舵颤振运动方程如下。
空气舵的一般运动z(x,y,t)可以表示为多阶模态振型fi(x,y)及其广义坐标qi(t)的函数:
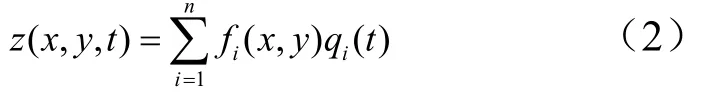
空气舵动能为
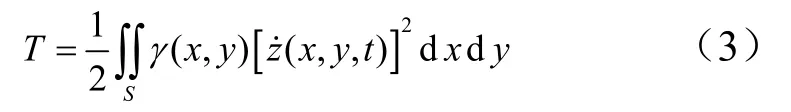
式中γ(x,y)为舵面单位面积的质量;积分域S为舵面面积。上式的矩阵形式为
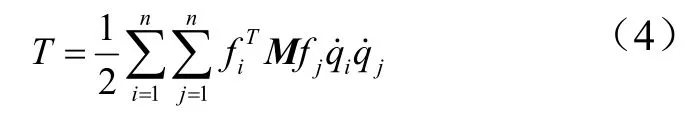
根据固有振型的正交条件:

则有:

空气舵的变形势能为
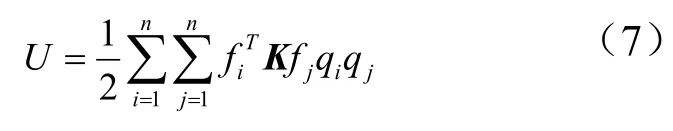
同样,根据固有振型的正交条件:

则有:
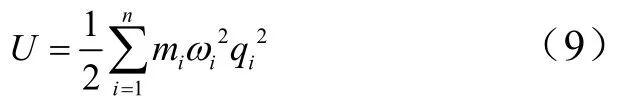
舵面上压力分布表示为p(x,y,t),按照广义力的定义,当舵面有虚位移δqi时,系统做的虚功为
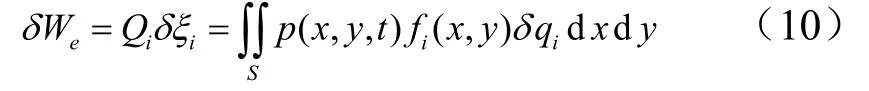
固广义力为
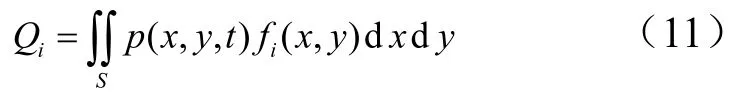
将式(4)、式(7)、式(11)代入拉格朗日方程:
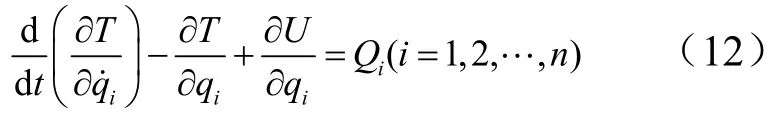
即可得到颤振运动方程:
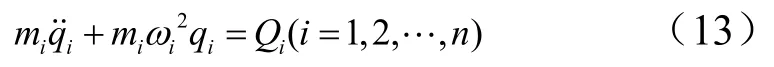
2.2 非定常气动力
ZAERO采用高超声速统一升力面理论来计算非定常气动力,将升力面分成若干个两侧边平行于来流的梯形块,并认为每小块上的空气动力作用在分块的压力点上,边界条件则在下洗控制点处得到满足。舵系统非定常气动力网格如图3所示。
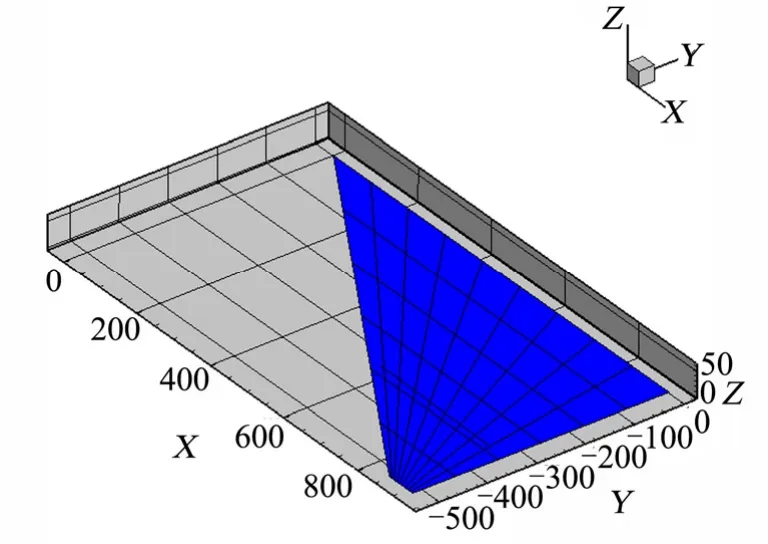
图3 升力面网格划分示意Fig.3 Schematic Diagram of Lifting Surface Mesh
由非定常气动力理论可知,对于每个网格的下洗控制点应满足下列积分方程:
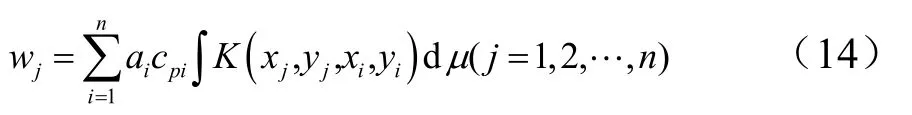
式中wj为第j个网格下洗控制点处的下洗速度;K(xj,yj,xi,yi)为由非定常超音速气动力理论得到的核函数;ai为常系数;n为升力面的气动网格分块数。
式(14)可化为矩阵形式,基本方程为

式中w为气动网格控制点的下洗速度,w=[w1…wn]T;Δp为气动网格的压力分布,Δp=[Δp1…Δpn]T;D为非定常气动力影响系数矩阵。
对于薄翼面,各气动网格H点的下洗速度与振动模态有下列关系:

式中q为模态坐标向量,q=[q1…qm]T;FH为控制点的模态矩阵;k为减缩频率;b为参考长度。
将式(16)代入式(15)中,可以得到:

式中P为非定常压力系数矩阵,其表达式为

根据广义气动力的定义,其矩阵表达形式为

式中FP为网格气动作用点处的模态矩阵;S为面积加权阵,S=diag(ΔS1,…,ΔSn),对角项为各气动网格的面积。
将式(17)代入式(19)中,可得:

式中A为广义气动力系数矩阵:
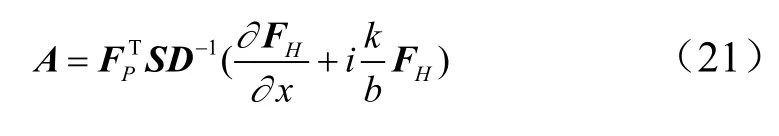
3 分析结果及总结
以模态试验获得的空气舵系统两阶频率、质量、振型为输入,假设结构阻尼为零,采用ZAERO开展分析,计算马赫数为5时空气舵颤振动压,得到各个状态的分析结果如表3所示。

表3 颤振分析结果Tab.3 Flutter Analysis Results
由表3中数据可见:
a)20 kg负载、80 N激振力工况模态质量测量异常偏大,20 kg负载工况振型与图2相比发生了明显变化,剃除这2种工况,则随着弯、扭频率差的增大,颤振动压也随之增大,如图4所示。
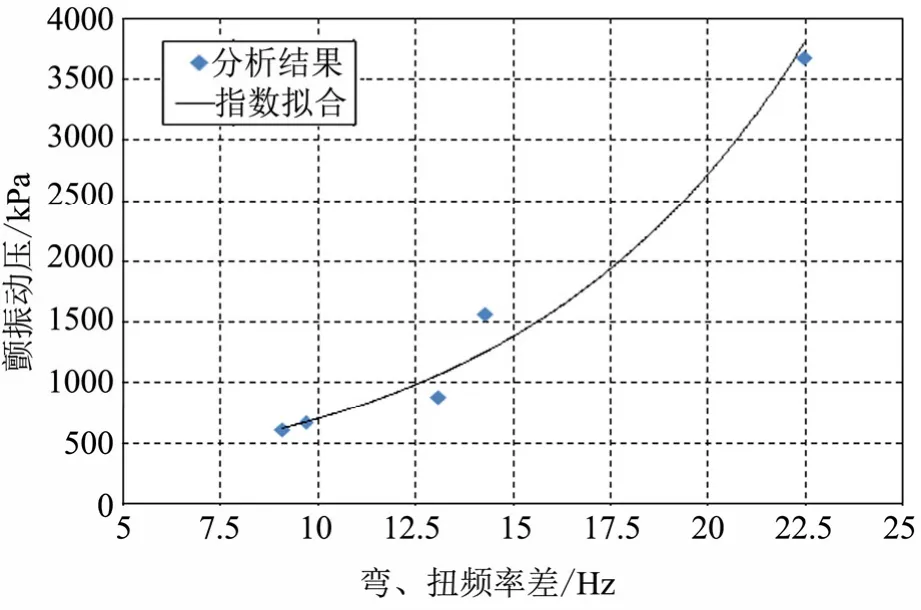
图4 弯、扭频率差-颤振动压关系曲线Fig.4 Difference of Flexural and Torsional Frequency-flutter Dynamic Pressure
b)频率差最小9.1 Hz,颤振动压为612.5 kPa,频率差最大22.5 Hz,颤振动压为3676.531 kPa。由于非线性模态数据的不确定导致的颤振动压相差可以达到6倍,严重影响颤振设计的精度。
c)在频率差相近时,颤振动压与频率高低并没有直接关系。频率差为9.1 Hz和9.7 Hz的两组数据,激振力幅值为20 N时频率明显高于60 N时频率,但是颤振动压却略小于60 N状态,与频率差的规律一致。
d)目前的工程实践中,对于非线性的空气舵系统颤振问题,一般采用保守设计的思路,要求对所有模态状态中最危险的情况进行分析,保证在该状态下空气舵也不会发生颤振失稳。本文中空气舵系统马赫数为5时的最低颤振动压为612.5 kPa,其v-g、v-f如图5所示,颤振形式为弯、扭耦合的突发颤振。
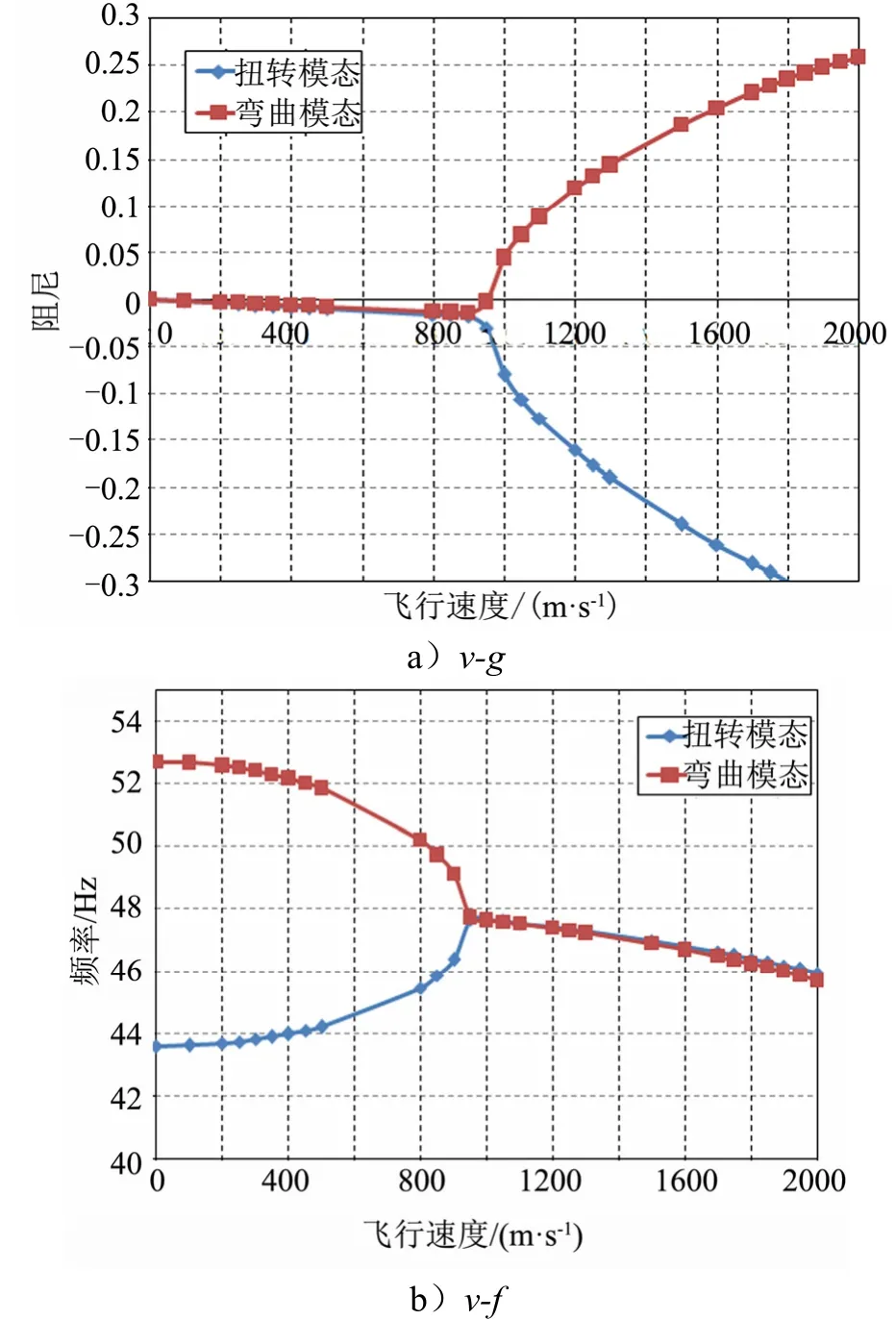
图5 50kg负载、20N激振力工况v-g、v-f关系曲线Fig.5v-g、v-f under 50kg Loading, 20N Exciting Force Condition
4 后续研究思路
由上述研究过程可见,采用传统的线性模态识别方法对非线性空气舵系统进行模态试验获得的数据存在较大的不确定性,会进一步影响颤振分析的结果,后续需要对试验方法和分析方法开展研究:
试验方法研究一方面探索采用纯模态、非线性模态等试验方法来表征非线性结构的动特性,另一方面可通过对标定过的不同间隙、摩擦状态的空气舵试验件开展风洞颤振试验,获得空气舵的真实颤振速度,与颤振分析结果对比,来寻找更加合理的颤振设计思路。分析方法研究可在现有工程分析方法的基础上引入间隙、摩擦的数学模型开展分析,但是分析结果的正确性仍然有待风洞颤振试验的验证。
5 结束语
在飞行器设计过程中,间隙、摩擦等因素造成空气舵系统的动特性存在明显的非线性,以某空气舵系统为研究对象,获得了其动特性随激振力幅值和负载的变化规律,研究了颤振动压随弯、扭两阶频率的变化规律,指出若按照当前常用的保守设计方法,即保证空气舵在所有模态试验工况下均不发生颤振,则颤振动压存在较大的散布范围,最小颤振动压仅是最大颤振动压的1/6。工程设计亟需对空气舵的非线性进行深入研究,将分析与试验相结合,来给出更精确的设计思路和方法。

