二次受力下外包钢筋RPC加固钢梁抗剪性能研究

卜良桃，刘伟

(湖南大学土木工程学院，湖南长沙 410082)

活性粉末混凝土(reactive powder concrete，RPC)属于超高性能混凝土(UHPC)[1]，是一种具有超高抗压强度、较高抗拉强度、良好冲击韧性和耐久性的新型水泥基复合材料[2]。RPC 不仅身为钢桥面混凝土广泛应用于桥梁建筑，而且作为高技术混凝土在房建加固领域同样有着广阔的发展空间，急切需要推广应用。卜良桃等[3]通过型钢混凝土(RPC)短柱拔出试验表明RPC 和型钢共同工作性能良好，为该加固方法可行性提供了依据。外包钢筋RPC 加固钢结构方法与传统[4]焊接加固和黏贴预应力纤维增强复合材料加固方法比较，具有以下明显优势[5-8]：1) 有效解决加固后钢结构防火和耐腐蚀性差等问题；2) 加固过程中不会产生局部高温等对钢构件造成二次损伤；3) 加固后构件极限承载力提升幅度大，加固效果明显；4) RPC 中不含石子等粗骨料和添加高强微细钢纤维的组成特点使构件耗能和延性增强。目前，国内外学者对超高性能混凝土加固钢梁的抗剪性能和影响因素等进行了研究[9-10]，给出了加固梁抗剪承载力计算公式[11-12]。然而这些抗剪加固试验都是在一次受力下进行，而建筑结构加固之前其构件已承受荷载且加固时荷载难以完全移除。此外，考虑实际工程中二次受力影响可使新增加固材料用量减少，结构脆性减弱[13]。同时对于外包钢筋RPC 加固补强钢构件二次受力的抗剪研究尚无先例且缺乏较为系统的分析及较为准确的承载力计算公式。于是，对加固后组合构件的二次受力抗剪性能进行全面系统的研究尤显重要。基于此，以对抗剪性能影响显著的剪跨比、考虑二次受力的初始荷载和反映不同型钢截面的含钢率为试件主要变化参数进行抗剪试验研究，给出抗剪承载力建议公式，以期为钢筋RPC 外包加固技术在设计计算和工程应用中提供参考。

1 试验概况

1.1 加固概念

二次受力下外包钢筋RPC 加固钢梁技术是钢梁四周布置完钢筋持荷情况下，对其左右下3 面U形支模浇筑RPC，增大原钢梁截面面积，使RPC和钢梁共同承担新增荷载以达到提高承载力和耐久性目的。周乐等[14]采用负载下外包钢筋混凝土加固钢柱技术对加固柱轴压性能进行试验研究，为该加固技术提供了参考。

此加固技术主要步骤如下：钢梁四周布置钢筋—钢梁一次受力—持荷支模—浇筑RPC—养护(间隔0.5 h洒热水养护3 d)—拆模—自然养护25 d。

1.2 试件设计

共设计6 根足尺抗剪试验梁，包括1 根对比钢梁GL 和5 根二次受力下加固梁SRL1～SRL5。加固梁截面尺寸皆为b×h=200 mm×400 mm，长度为4 500 mm，支座两端各外伸100 mm，支座位置依据设计剪跨比确定。原钢梁截面规格为I32a 和I32b，强度等级为Q235。RPC 设计强度等级为R120，型钢梁底、顶对称配置2C12 纵筋及B8@200 箍筋沿梁通长布置。试验以剪跨比、初始荷载和含钢率为设计参数具体见表1。试验加固梁截面详细尺寸及配筋见图1，型钢上下保护层厚度为40 mm，左右保护层厚度为35 mm。

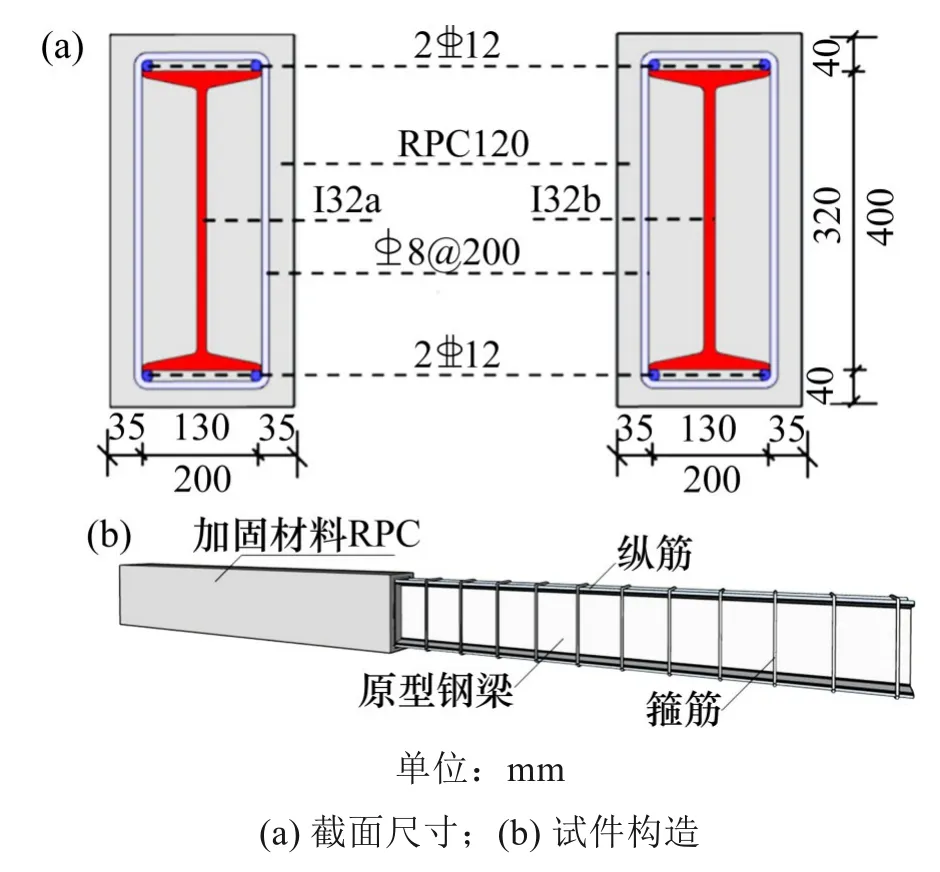
图1 加固试件截面尺寸和构造Fig.1 Dimensions and details of reinforced specimens

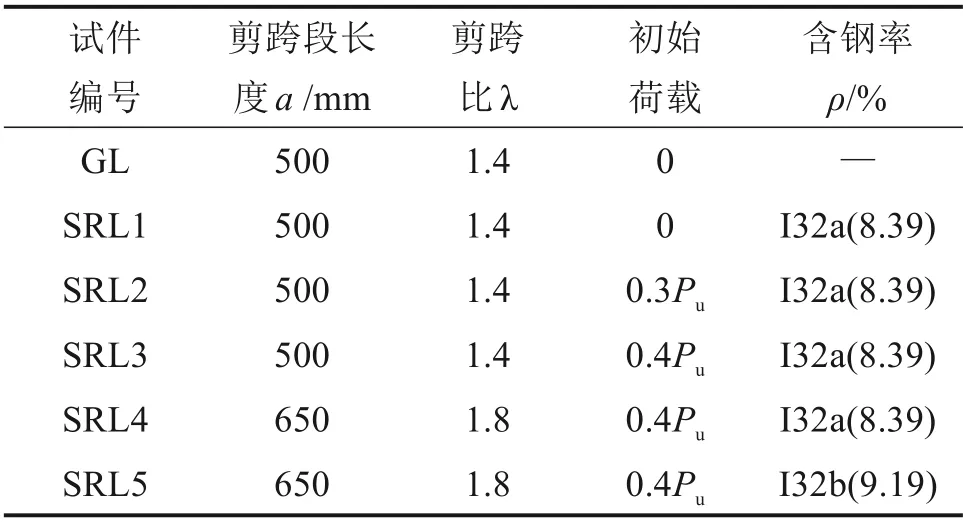
表1 试验梁主要参数Table 1 Main parameters of the test beams

采用湖南固力工程新材料有限责任公司生产的具有固定配合比RPC 干混料。为确定RPC 材料力学性能，浇筑时预留100 mm×100 mm×100 mm试块2 组，100 mm×100 mm×300 mm 试块4 组，置于试件旁同条件养护。按照规范[16]实测RPC 立方体抗压强度平均值fcu=122.3 MPa，轴心抗压强度平均值fc=103.7 MPa， 轴心抗拉强度根据ft=2.14fc- 12.8，得ft=9.0 MPa，弹性模量Ec=43 100 MPa。 纵筋和箍筋分别采用HRB400 和HRB335 级钢筋，纵筋点焊于型钢上下翼缘，箍筋采用扎丝与纵筋绑扎连接，钢材力学性能见表2。

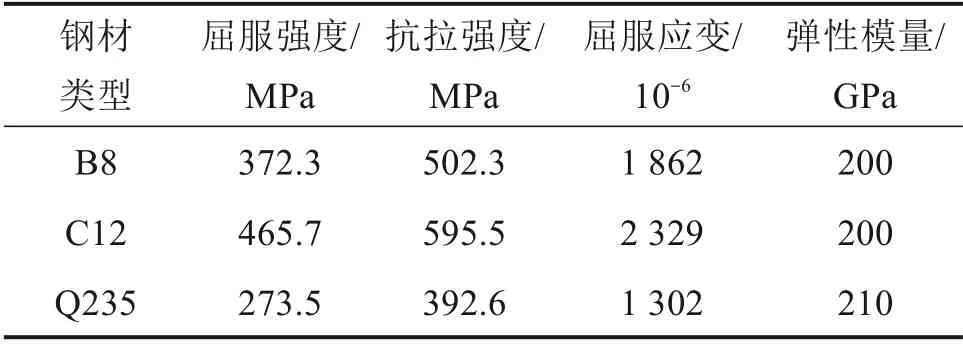
表2 钢材力学性能Table 2 Mechanical properties of steels

1.3 加载方案和测点布置

实际工程中多数构件为反弯构件，集中荷载作用下钢筋混凝土梁抗剪承载力比同条件简支梁低约28%，偏于不安全。因此，试件采用伸臂四点加载进行静力试验见图2，在集中荷载加载点和支座处加垫40 mm 厚钢垫块防备钢梁局部屈曲。考虑到二次受力问题全过程分为2个加载阶段，一次受力和二次受力阶段，加载前实施预加载确保仪器正常工作。试验采用单调静力加载制度，一次受力阶段分级加载至预定初始荷载，为防止支模浇筑RPC 期间荷载卸退需用预制钢板将千斤顶底和顶之间顶紧。二次受力阶段先加至初始荷载撤掉钢板，正式实施分级加载，液压千斤顶每级荷载增量为100 kN，每级持荷10 min。当荷载达到预算极限荷载的90%时，每级荷载增量为50 kN，直至缓慢将试件破坏。对比梁GL直接分级加载至腹板屈服得极限承载力为937 kN，与计算结果902 kN 基本一致，为和剪跨比1.8试件保持统一表1中Pu均取计算的设计值。

压力传感器测取试件承受荷载，挠度由集中荷载加载点和支座处布置的4个百分表量测见图2，其他相关应变通过相应布置的应变片测得。试件应变测点布置见图3，其中，RF 和RG 以及SF 和SG 分别表示RPC 和型钢腹板表面贴的应变花和应变片，G1 和Z1 表示1 号箍筋和1 号纵筋上的应变片。

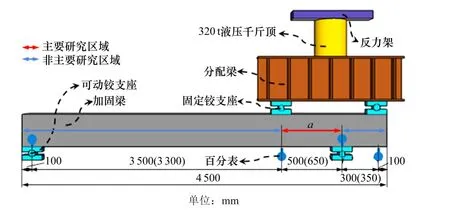
图2 加载装置Fig.2 Test setup

图3 试件应变片布置Fig.3 Layout of strain gauges of specimens

2 试验结果分析

2.1 破坏形态

为研究钢梁采用外包钢筋RPC 增强后的整体受剪性能，加固梁试验前均通过抗弯抗剪计算以保证“强弯弱剪”设计，最终加固试件均发生剪压破坏。试件最终破坏形态为：A 支座梁顶和B 加载点梁底附近出现向腹板中部延伸受弯裂缝，其间伴有支裂缝；两弯剪区均呈现斜裂缝，A 和B 剪跨段发生主斜裂缝，穿过的箍筋和型钢腹板屈服，缝间可见交错变形的外露钢纤维，主斜裂缝附近出现多条走势一致斜裂缝，缝宽较小；A支座处受压RPC轻微外鼓。

试件破坏过程基本一致，以SRL4 为例进行现象描述，文中荷载均已减去初始荷载，重点研究二次受力阶段。二次受力初始时，试件无明显变形无裂缝，加载至380 kN 时，负弯矩区域A 支座截面顶部拉应力达到RPC 抗拉强度出现首条竖向受弯裂缝，加载至480 kN 时B 加载点梁底出现受弯裂缝，荷载增加裂缝延伸，出现新增裂缝。加载至680 kN 时，左弯剪区腹板中部出现初始斜裂缝，荷载加大，裂缝近似沿AB 连线方向开展，之后斜裂缝附近陆续出现多条与其近似平行斜裂缝。临近极限荷载时，斜裂缝宽度增大贯穿腹板形成临界斜裂缝，最终液压千斤顶荷载无法继续上升，标志试验结束，典型试件破坏形态见图4。整个加载期间不时伴有钢纤维被拉断的“吱吱”声，由于钢纤维与RPC 黏结力存在裂缝整体呈“细而密”特征，斜裂缝最大宽度为3.6 mm 远小于普通钢筋混凝土梁临界缝宽。

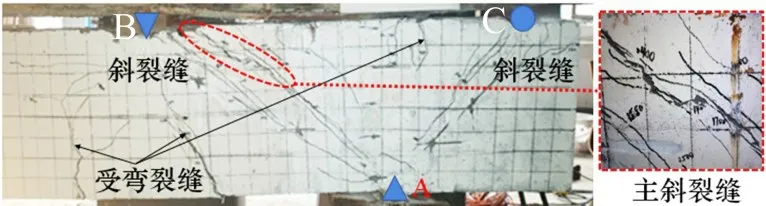
图4 试件典型破坏形态Fig.4 Typical failure patterns of specimen

2.2 荷载-挠度曲线

加固梁与型钢混凝土梁整个破坏过程基本一致，全过程划分为3个阶段：未开裂阶段、裂缝开展阶段和破坏阶段。二次受力初始时，荷载-挠度曲线呈线性梁处于弹性未开裂阶段。当荷载加至极限荷载的30.71%～33.57%时出现斜裂缝，曲线斜率并未立即减小而是在约200 kN 后微降，其原因为结构致密RPC 中随机分布的钢纤维发挥“桥联”作用承担了裂缝处拉应力抑制裂缝开展提升梁剪切刚度。随荷载增加，竖向裂缝和斜裂缝新增并扩展延伸，裂缝加宽，挠度变大，刚度减弱，梁处于裂缝开展阶段。加载到极限荷载74.8%～83.3%时，基本无新增裂缝，挠度增长明显加快，斜裂缝贯穿腹板且穿过的型钢和箍筋屈服，最终破坏时试件保持较好完整性。

按照设计参数不同分组做出试件荷载-挠度(取B 支座挠度)曲线见图5。观察曲线发现，加固梁破坏阶段荷载并未呈现下降趋势，表现出稍平稳发展趋势且剪跨比越大此趋势越明显，表明试件最终未发生局部失稳破坏。设计试件SRL1～SRL3型钢初始荷载与设计荷载比值μ分别为0，0.3 和0.4，用于分析初始荷载对加固梁抗剪性能的影响，荷载-挠度曲线见图5(a)。加固梁曲线处于钢梁GL上，说明加固梁耗能性能得到极大改善，这与试验过程中钢纤维拉断拔出吸收能量不无关系。较大的初始荷载对加固钢梁承载力提高幅度反而减小，对比直接加固试件SRL1，二次受力加固试件SRL2 和SRL3 极限承载力分别减幅8.91% 和12.46%。这是初始荷载使型钢率先产生应力，相对外包RPC 和钢筋始终存在应力超前现象，初始荷载越大，应力越超前，型钢屈服越早，新增材料利用率越低，承载力随之降低。试件SRL2 和SRL3 相较于SRL1 弹性未开裂阶段缩短，表明试件剪切刚度变小速度加快，推测原因为初始荷载加速型钢屈服，上下翼缘对核心区RPC 约束作用减弱，梁整体刚度减小。综上，初始荷载对型钢外包钢筋RPC 加固起不利作用，加固时应尽量使型钢卸载充分利用新增材料强度。

不同剪跨比对加固梁荷载-挠度曲线影响见图5(b)，初始荷载和含钢率均相同的试件SRL3 和SRL4 剪跨比分别为1.4 和1.8。梁极限承载力随剪跨比的增加而降低，剪跨比增加0.4，试件SRL4抗剪承载力比试件SRL3 降低9.03%。在前期弹性未开裂阶段曲线基本重合，表明剪跨比对前期抗剪刚度影响微弱，随试验进程推进，曲线越来越分离，影响越来越大。

型钢截面规格为I32a 和I32b 的试件SRL4 和SRL5荷载-挠度对比曲线见图5(c)，外包RPC对含钢量较大的截面加固效果更好。试件SRL5 承载力比试件SRL4 提高1.05 倍，原因为含钢率的增加主要为型钢腹板厚度的增加，一方面，型钢随腹板厚度增加直接提升自身抗剪贡献；另一方面，配合钢梁翼缘对核心区RPC 约束作用增强，延缓试件剪切刚度减弱提高整体性能，间接提升抗剪承载力。曲线前2个阶段基本重合，表明含钢率对加固梁基本没有影响，这是因为型钢弹性模量接近，对试件整体刚度影响相近，在破坏阶段含钢率差异导致曲线分离。

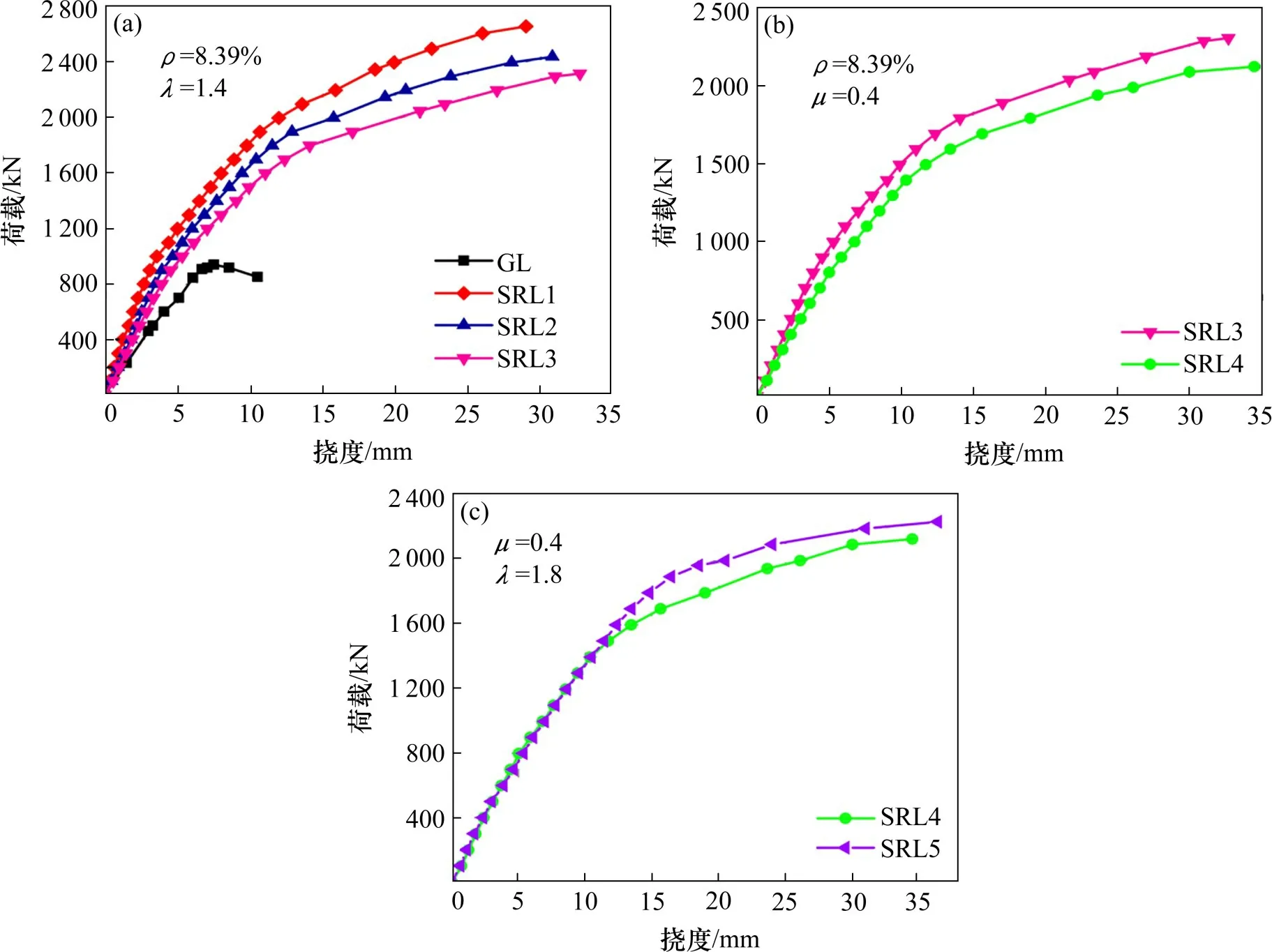
图5 荷载-挠度曲线Fig.5 Load-deflection curves

2.3 应变分析

试件受剪过程中斜截面会发生应力重分布现象，以试件SRL3 为例进行说明，其斜截面箍筋和型钢腹板荷载-应变曲线见图6。斜裂缝出现(荷载为750 kN)前，箍筋和型钢腹板曲线线性增长应变很小，截面剪力主要由RPC 负担。斜裂缝出现后主斜裂缝出现前，随荷载增大曲线斜率稍减，此时截面剪应力发生第1次重分布，RPC 将部分剪力转移给穿过的箍筋和型钢。同一水平荷载下，型钢腹板应变约为箍筋2倍且曲线斜率接近，说明型钢腹板比箍筋早屈服同时对抗剪贡献更大。型钢腹板屈服时发生第2次应力重分布，型钢屈服荷载增加应力基本不变将剪力传递给外包RPC 和箍筋，其中第2 次应力重分布较第1 次明显。主斜裂缝出现后应变快速增加，最终箍筋和型钢腹板应变分别大于3 500 με 和5 900 με，均超过屈服应变，强度得以充分利用，但由于钢纤维黏结和型钢翼缘对核心区RPC 约束作用，斜裂缝间RPC 并未退出工作，此时试件仍具一定承载力，破坏时剪压区RPC 测点RF2 应变为2 636 με，可见RPC 未达到极限压应变，抗压强度未被充分利用。

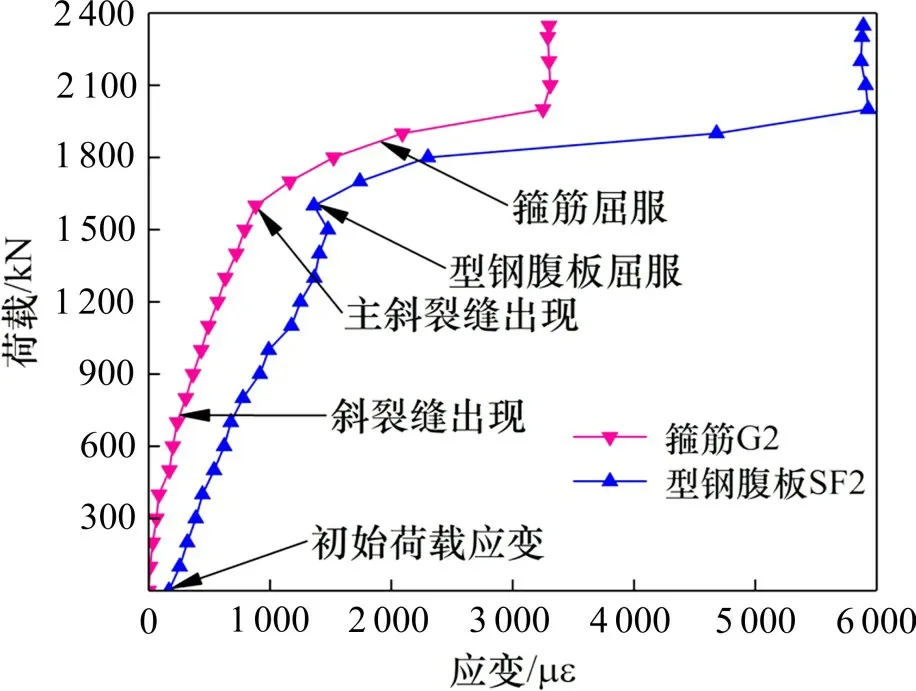
图6 SRL3箍筋和型钢腹板荷载-应变曲线Fig.6 Load-strain curves of SRL3 stirrup and steel web

2.4 型钢外包钢筋RPC加固性能分析

试件斜裂缝开裂荷载与极限荷载比值见图7，图中参考线表示普通型钢混凝土梁的斜裂缝开裂荷载约为极限荷载的15%，而外包RPC 加固钢梁的斜裂缝开裂荷载与极限荷载比值均为前者的2倍以上，表明加固梁抗裂性能优于普通型钢混凝土梁。这是RPC 中掺入钢纤维具有较高抗拉强度有效延缓试件开裂的结果。分析图5(a)可得，对比钢梁加固梁的曲线斜率更陡，说明外包钢筋RPC 加固能有效提高原钢梁剪切刚度。主要原因有2个方面[17]，一是新增RPC 表现出尺寸叠加效应直接提高了钢梁刚度，二是型钢翼缘有效约束住核心区RPC，同时RPC 为型钢腹板及翼缘提供可靠的侧向支撑，两者相辅相成减缓加固梁截面刚度的弱化，间接提高了钢梁刚度。加固钢梁抗剪承载力最大提高幅度达到2.8倍，加固效果显著。

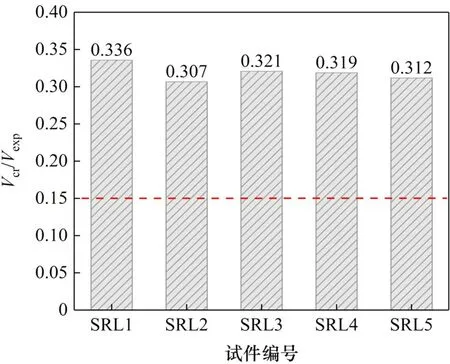
图7 试件出现斜裂缝荷载与极限荷载比值Fig.7 Ratio of the appearing oblique crack load and ultimate load

3 抗剪承载力计算

目前，国内外学者还未给出关于二次受力下外包钢筋RPC 加固钢梁足尺构件斜截面抗剪承载力计算公式，依据我国现行《组合结构设计规范》JGJ 138[18](以下简称《规范》)5.2.5-3 计算结果见表3，材料性能均取实测值。分析表3 可知，试验值与其平均比值为1.67，表明计算值严重偏离试验值难以准确反映试验结果。分析原因有二：一是《规范》适用于C20～C80 混凝土；二是未考虑斜裂缝处微细钢纤维抗剪贡献和剪压区RPC 未达到峰值应力的折减。

文中采用型钢腹板抗剪贡献、箍筋和RPC 抗剪贡献三者叠加对加固梁斜截面抗剪承载力进行计算，但实际抗剪结果绝不是三者数值的机械叠加，彼此相互影响耦合。针对上述偏差较大原因文中给出解决措施，依据试验数据重新拟合出合适的材料抗力系数；利用折减系数ψ考虑对RPC抗压强度折减。将型钢翼缘和纵筋抗剪贡献作为安全储备，在公式中不予考虑。借鉴《规范》，考虑设计参数，取用式(1)数学模型进行多元回归分析：

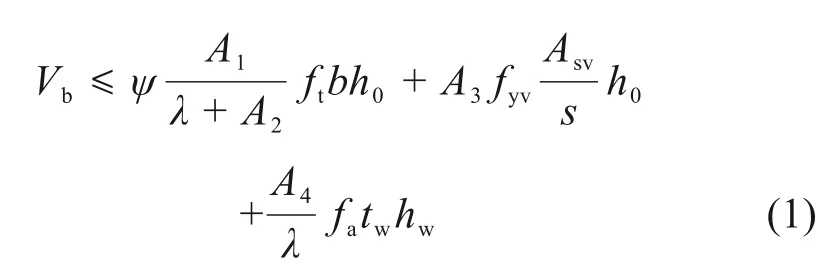
式中：ψ为RPC 抗压强度折减系数；A1，A2，A3和A4为待定系数；其余参数和《规范》规定相同。

分析试验结果，型钢初始荷载和RPC 折减系数为负相关关系，即初始荷载越大，折减系数越小。推导折减系数ψ过程中，由于剪压区RPC 处于较复杂的应力状态，为简化计算，结合文献[5]提出以下基本假定：1) 加固梁二次受力期间型钢与外包RPC 不发生黏结滑移，即型钢腹板和RPC应变量相同；2) 剪压区RPC 承受剪、压、弯等复合应力，因研究RPC 抗压强度利用率，则将剪压段近似视为轴压构件；3)结合第2.3 节中箍筋和型钢腹板荷载-应变曲线近似双折线，则钢材本构取用双折线随动强化模型；4)RPC 受压应力-应变关系取文献[19]建议曲线。具体推导过程见式(2)：

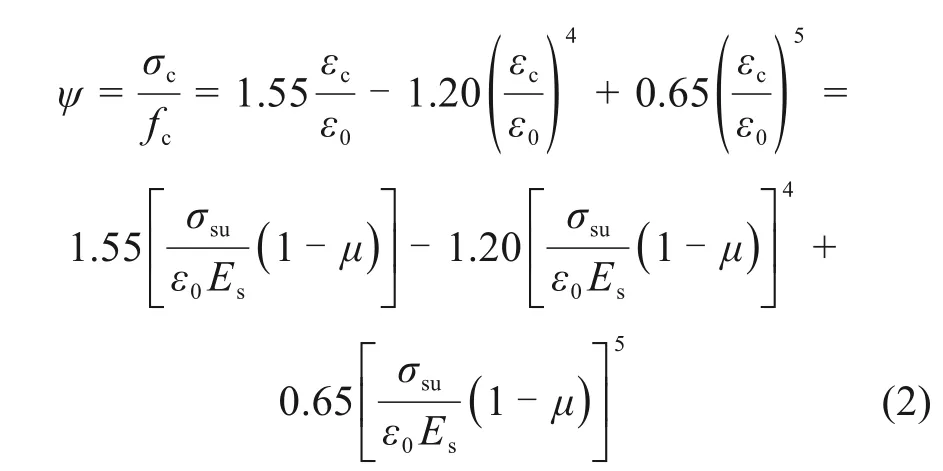
式中：fc，σc和εc分别为RPC 抗压强度、压应力和压应变；ε0为RPC 压应力达到fc时峰值应变，取ε0= 0.002 92；σsu，Es分别为型钢极限应力和弹性模量；μ为型钢初始荷载占荷载设计值百分比。

将折减系数代入式(1)，结合试验数据进行回归分析得A1=3.0，A2=A3=1.0，A4=1.35，则最终加固梁斜截面抗剪承载力计算公式为：

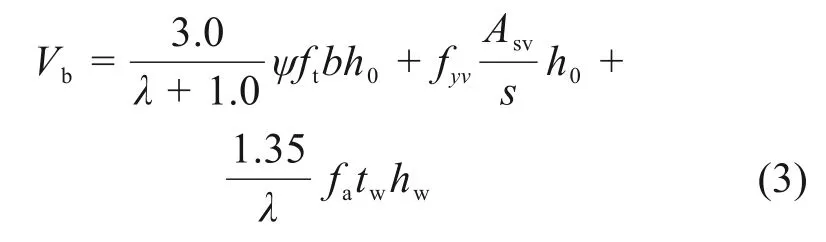
对于剪跨比λ< 1.5 取λ= 1.5；剪跨比λ> 3.0取λ= 3.0。将加固试件材料实测值代入式(3)进行计算，试验值与计算值的平均比值为1.06，变异系数为0.04，说明拟合效果良好且具有一定的安全储备。

4 有限元分析

4.1 模型建立

采用有限元软件ABAQUS 建模进行非线性分析，模拟与试验相互验证对比分析。RPC 和型钢选用8 节点六面体线性减缩积分实体C3D8R 单元，钢筋选用2 节点线性三维桁架T3D2 单元[20]，各材料本构模型与抗剪承载力计算基本假定保持一致，建模时材料本构数据均取文中实测值。外包RPC定义ABAQUS 软件自带的混凝土损伤塑性模型(CDPM)，该模型能较好模拟RPC 开裂和抗剪破坏时特性。RPC 与钢筋骨架采用内置(Embedded)约束，RPC 与型钢接触面采用绑定(Tie)约束，保证其共同受力位移协调，钢筋骨架与型钢采用结点绑定(Tie)约束，施加荷载参考点RP-1 和RP-2 与型钢表面耦合。边界约束按试验情况采用一端固定铰支约束(U1=U2=U3=UR1=0)，另一端为去除X方向位移约束的可动铰支约束(即不约束U1)。有限元模型见图8。

图8 有限元分析模型Fig.8 FEA model

为有效模拟加固梁二次受力，采用“生死单元法”分别用2 个分析步模拟其加载过程[21]，具体分析见图9。分析步1 采用荷载控制加载模拟型钢梁初始荷载，使用关键字“Model Change，Remove”命令将外包RPC 和钢筋骨架单元“杀死”以保证型钢梁单独受力；分析步2采用位移控制加载模拟加固梁二次受力，使用关键字“Model Change，Add”命令将RPC 和钢筋骨架单元“复生”以保证三者共同受力破坏。

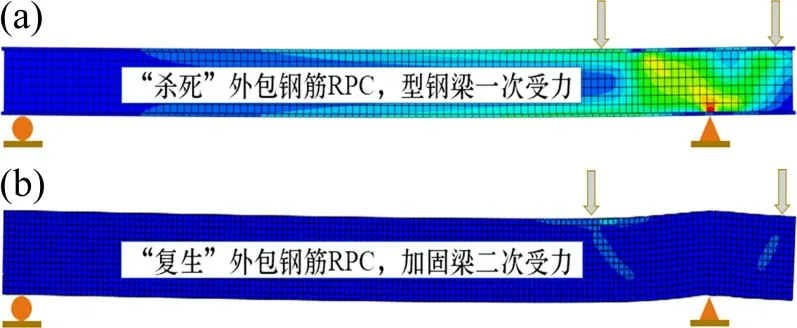
图9 有限元分析示意Fig.9 Sketch of FEA

4.2 试验和有限元结果对比分析

为验证有限元模型合理性，将有限元模拟结果与试验实测结果进行对比分析。试件极限承载力对比结果见表3，试验值与模拟值平均比值为0.95，变异系数为0.05，误差较小。试件荷载-位移曲线对比结果见图10，各试件曲线吻合较好且随剪跨比增大吻合程度越高，有限元结果能较好模拟试件各个受力阶段，针对有限元模拟刚度略大于试验值，主要原因为模型中未考虑外包RPC和型钢接触面黏结滑移、支座约束条件与试验实际存在差异及有限元中材料更加理想均匀内部缺陷少。试件破坏损伤对比结果见图11，模拟损伤结果与试验破坏现象相符，裂缝开展与试验过程一致，负弯矩区RPC 拉伸损伤出现受弯裂缝，支座处局部受压损伤，左右剪跨区出现斜裂缝。整体来看，有限元模型建立合理，能有效模拟加固梁力学性能。

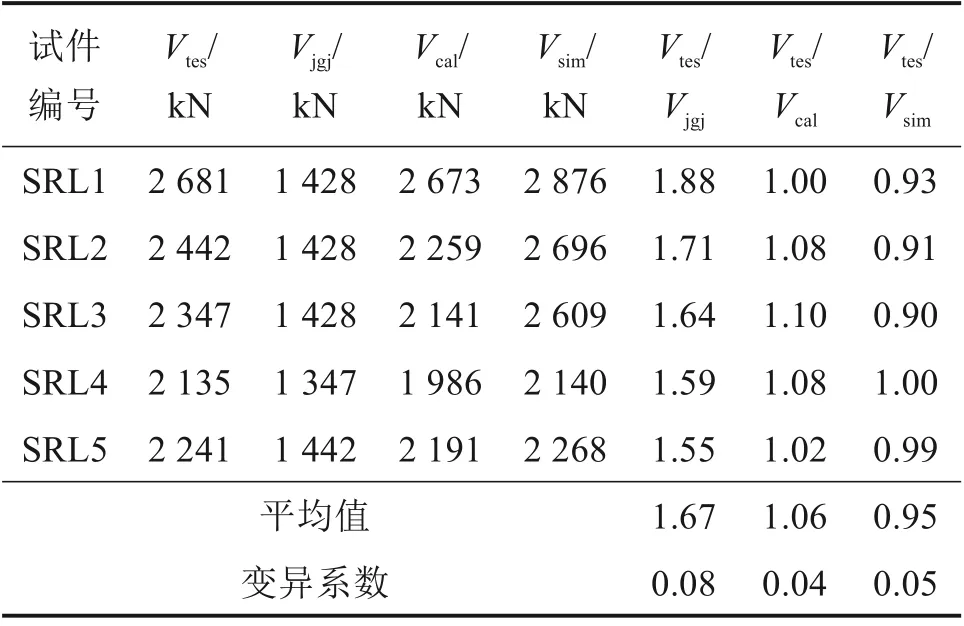
表3 试验、有限元和计算结果对比Table 3 Comparison of test,FE and calculated results

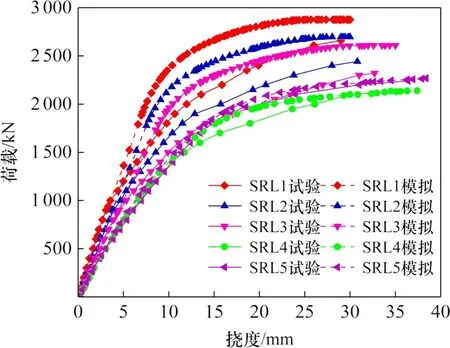
图10 有限元与试验荷载-挠度曲线对比Fig.10 Comparison of load-deflection curves between FEA and test

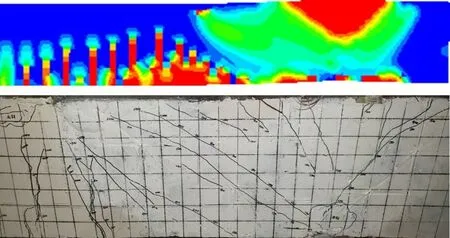
图11 SRL5试件有限元与试验现象对比Fig.11 Comparison of FEM and test phenomena for SRL5

5 结论

1) 二次受力下外包钢筋RPC 加固钢梁抗剪承载力最大提高幅度达到2.8 倍，破坏后RPC 与型钢表面未发生明显黏结滑移破坏，其协同工作性能良好。

2) 各加固试件均发生剪压破坏，其受力破坏过程可划分3 个阶段。剪跨比1.4～1.8 范围内，试件抗剪承载力提高程度随剪跨比和初始荷载增大而减小。外包RPC 对含钢量较大的截面加固效果更好。

3) 考虑RPC 抗压强度折减，基于试验结果通过拟合给出加固梁斜截面抗剪承载力建议公式，计算结果和有限元模拟结果均与试验数据吻合良好，可为加固工程提供一定理论依据。