一种适用于变轴力柱混合试验的改进BWBN模型及其参数识别

郭玉荣，潘洪军

(1. 湖南大学土木工程学院，湖南长沙 410082；2. 建筑安全与节能教育部重点实验室，湖南长沙 410082)

RC 柱在地震作用下，随着损伤的累计，通常会表现出强度、刚度退化以及捏拢效应等滞回特点。为了描述这些现象，有许多学者进行研究并提出了相应的恢复力模型。WEN[1]提出了光滑曲线模型。BABER 等[2-3]将刚度、强度退化以及捏拢效应参数引入Bouc-Wen 模型，提出了BWBN 模型，因其属于光滑的曲线模型且能较好描述构件的退化特点得到了广泛运用。为了让BWBN 模型能更好地描述不同构件的性能，许多学者对BWBN 模型进行了改进工作。余波等[4-5]提出了一种双轴和平扭耦联的BWBN 模型，并通过引入参数δ实现滞回曲线上下平移来描述不对称滞回现象；SENGUPTA 等[6]引入滞回最大位移改进屈服后刚度来描述梁柱节点的滞回性能；PELLICIARI 等[7]提出了新的刚度、强度退化参数，并以高斯分布函数来代替BWBN 模型中的捏拢效应相关项，大大减少了模型参数。以上都是在定轴力下RC 柱的恢复力模型改进工作。但实际上，在地震作用过程中，框架结构的边柱或角柱轴力会因地震倾覆力矩而发生不断变化，而近场地震的竖向地震分量也会导致柱轴力发生显著变化[8]。对于变轴力柱的性能，一些学者也进行了研究。HUGO 等[8]进行了6根RC 柱拟静力试验，发现相同破坏状态下变轴力试件破坏早于定轴力试件；王德斌等[9]研究了RC柱在多维动荷载下的性能，发现变轴力会降低构件延性；陈嵘等[10]进行了6 个混凝土墩柱试验，发现变轴力柱破坏形式由最大轴力控制，且滞回曲线明显不对称。针对变轴力柱子特性，SHAYANFAR等[11]提出了一种梁柱节点的旋转弹簧模型，它可以有效考虑变轴力对节点和柱的影响。周小龙等[12-14]研究发现，柱子各种退化现象与损伤指标间有密切关系，并都建立了相应的恢复力模型。故本文将PARK-ANG 等[15]损伤模型引入到原始BWBN 模型中，提出了一种基于累计损伤的改进BWBN 模型。此外，为了进一步将改进模型用于变轴力情况，用轴力插值以及正负向单独计算损伤的方式来描述变轴力柱的滞回特点。目前，对变轴力恢复力模型和变轴力混合试验的研究尚少。提出的变轴力BWBN 模型由于能考虑轴力变化对柱子侧向滞回性能的影响，可进一步拓宽结构混合试验的应用范围，比如用于水平和竖向双向地震作用下的框架结构混合试验。

1 改进的BWBN模型

1.1 原始的BWBN模型

原始的BWBN模型表达式如下：

式中：δυ，δη分别为强度和刚度退化影响系数；ε为当前加载步下的构件累计滞回耗能；h(z)为控制滞回曲线捏拢程度的参数，计算方法见文献[2-3]。

1.2 定轴力下基于累计损伤的BWBN模型改进

选取美国太平洋地震工程研究中心(PEER)以及陆新征等[16]抗倒塌系列试验提供的共16 根柱子的数据，进行了相关规律总结，并对原始BWBN模型进行改进。其中，损伤计算采用吕大刚等[17]的改进模型。

1.2.1 强度退化系数

将每一滞回中的极限强度与试验全过程中的强度最大值的比值作为强度退化系数，其表达式如下：

式中：Pt为当前滞回的极限强度；Pt,max为试验全过程中的强度最大值。

16根柱子的强度退化系数如图1所示，可以发现，柱子的强度退化系数与损伤指标之间存在明显的二次函数关系。

图1 强度退化系数与损伤指标的关系Fig.1 Relationship between strength degradation coefficient and damage index

1.2.2 刚度退化系数

将正负向割线刚度与构件屈服刚度的比值作为刚度退化系数，其表达式如下：

式中：kt为正负向极限强度对应点的割线刚度；ky为构件屈服刚度。

16根柱子的刚度退化系数如图2所示，可以发现，柱子的刚度退化系数与损伤指标之间存在指数函数关系。

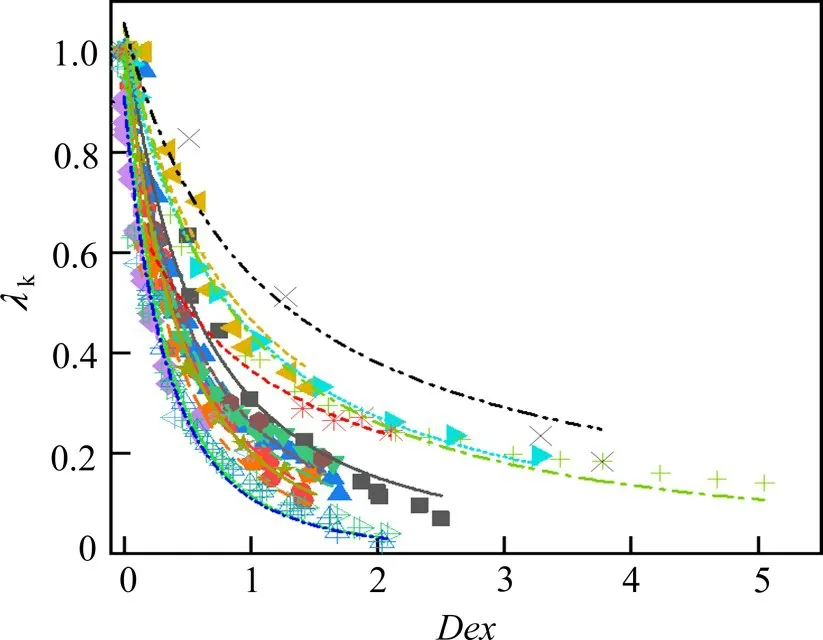
图2 刚度退化系数与损伤指标的关系Fig.2 Relationship between stiffness degradation coefficient and damage index

此外，对柱子滞回曲线进行观察发现，构件的屈服后刚度比α并不是一个定值。16根柱子的屈服后刚度比如图3所示，其与损伤指标大致存在反比例函数关系。但是，原始的BWBN 模型[2-3]却将其作为一个不变的值，所以对此进行了改进。

图3 屈服后刚度比与损伤指标的关系Fig.3 Relationship between stiffness ratio and damage indexafter yield

1.2.3 定轴力下BWBN模型改进

基于上述规律，本文对原始BWBN 模型中式(3)～(4)以及屈服后刚度比α进行了修正。

式中：Dex为损伤指标，值越大表示损伤越严重，当Dex≥1 时，认为构件破坏；β1为耗能因子；δm为构件在地震作用下的最大位移；δy，δu分别为单调荷载下的屈服和极限位移；Fy为构件的计算屈服强度；δ'υ，δ'η分别为强度、刚度退化影响系数；α0为构件初始屈服后刚度比；r为屈服后刚度退化率。

1.3 变轴力下BWBN模型改进

在构件受地震作用时，其轴力的变化会导致构件延性、强度、对称性等一系列性能产生变化。本文基于定轴力的改进模型也需要适当改变，采用一种将轴力分级并线性内插的方式来描述变轴力。

由于在计算损伤时需要先确定构件在单调荷载作用下的计算屈服力、屈服位移以及极限位移，所以本文按轴压比每0.05 一级计算构件的上述数据，区间内的轴压比就按线性插值计算其单调荷载下的性能。此外，对试验现象研究发现，柱子在地震作用下往往会表现为某一侧损坏严重，而另一侧损伤相对较小，此时损伤较严重侧的力学性能已经不如另一侧。因为总体损伤无法描述这种现象，所以本文将总体损伤分为正向与负向两侧的单侧损伤，对式(10)修正如下：

式中：Dex+(-)为正(负)向单侧损伤；δm+(-)为循环中正(负)向最大位移；ε+(-)为正(负)向单侧的累计滞回耗能。

2 改进BWBN模型的参数识别

2.1 基于CPSO-GA算法的参数识别方法

采用混沌粒子群—遗传算法混合算法(CPSOGA)来识别改进的模型参数，即在文献[18]的混沌粒子群算法基础上，利用文献[19]方法引入遗传算法。这种算法既保持了混沌优化算法的遍历性与随机性，还会在迭代时对父代种群进行选择、交叉及变异操作形成新的种群，有效避免了算法陷入局部最优。改进算法的流程如下：

1) 利用Logistic 方程，生成2N个初始个体，然后根据适应度函数值从中选取最优的N个个体作为初始解，并随机生成粒子速度。算法的适应度函数表达式如下：

式中：T为总加载步数；Fr(i)，Fm(i)分别为第i步时构件的实测恢复力以及模型计算恢复力。

2) 从初始N个粒子中选取适应度值最优的粒子作为种群全局历史最优值Pg，并把各个粒子当前位置作为个体历史最优值Pi。根据PSO 算法的速度和位置更新公式更新粒子的位置和飞行速度，更新公式表达式如下：

式中：vi(t)，zi(t)为粒子i的速度和位置；ω为惯性权重；η1，η2为加速常数；rand为0-1随机数。

3)利用文献[19]方法对当前种群进行选择、交叉及变异操作，对生成的新种群计算适应度函数值，与个体及全局历史最优解进行比较，若优于原最优解，则进行更新。

4) 对历史最优位置Pg进行混沌优化。先将Pg映射到Logistic 方程定义域[0,1]上(即zg=(Pg-ai)/(bi-ai)，其中bi，ai为变量上下界)，再根据Logistic 方程迭代产生m个混沌变量序列，并将序列映射返回优化变量的取值范围，得到m个粒子，根据适应度值得到最优解P′，用P′代替当前群体的任一粒子位置。

5) 返回第2 步，迭代至满足停止条件，输出结果。

2.2 参数识别结果

2.2.1 定轴力柱识别效果分析

选取PEER 上异于上述16 根柱子的试验数据，清华大学陆新征等[16]抗倒塌系列试验中边柱A 数据，以及湖南大学陈展[20]足尺柱变轴力试验的试验数据，对比分析模型改进的有效性。3 根柱子的参数如表1所示。其中：L为柱子长度；B，H为柱子截面宽高；f′c为混凝土轴心抗压强度；fyl为纵筋屈服强度；fyt为箍筋屈服强度；ρl为纵筋配筋率；ρt为箍筋配筋率；n0为轴压比。

表1 柱试件的基本参数Table 1 Basic parameters of the column specimen

利用改进PSO 算法识别原始与改进后BWBN模型参数，识别的参数如表2所示，对比结果如图4所示。

图4 改进前后BWBN模型识别效果对比Fig.4 Comparison of BWBN model identification effect before and after improvement

数学上经常用Pearson 相关系数来表示2 组数据之间的相关程度，一般认为其值超过0.8 即为强相关。本文利用Pearson 相关系数来评价模型改进前后的识别效果，相关性系数计算结果如表3所示。

表3 相关性系数统计Table 3 Correlation coefficient statistics

由上述分析可见，本文对于定轴力下BWBN模型的改进取得了良好的效果，改进后识别结果的相关性系数普遍高于原始模型。

2.2.2 变轴力柱识别效果分析

先确定轴力变化幅度，用纤维模型在OpenSees 建立图6(a)框架，进行了Taft，El Centro，天津波和唐山波下的双向地震作用时程分析，并结合文献[20]，确定轴压比范围0～0.7。对文献[20]变轴力柱进行识别，结果如表4中C4及图5所示。

表4 变轴力BWBN模型的识别参数Table 4 Identification parameters of variable axial force BWBN model

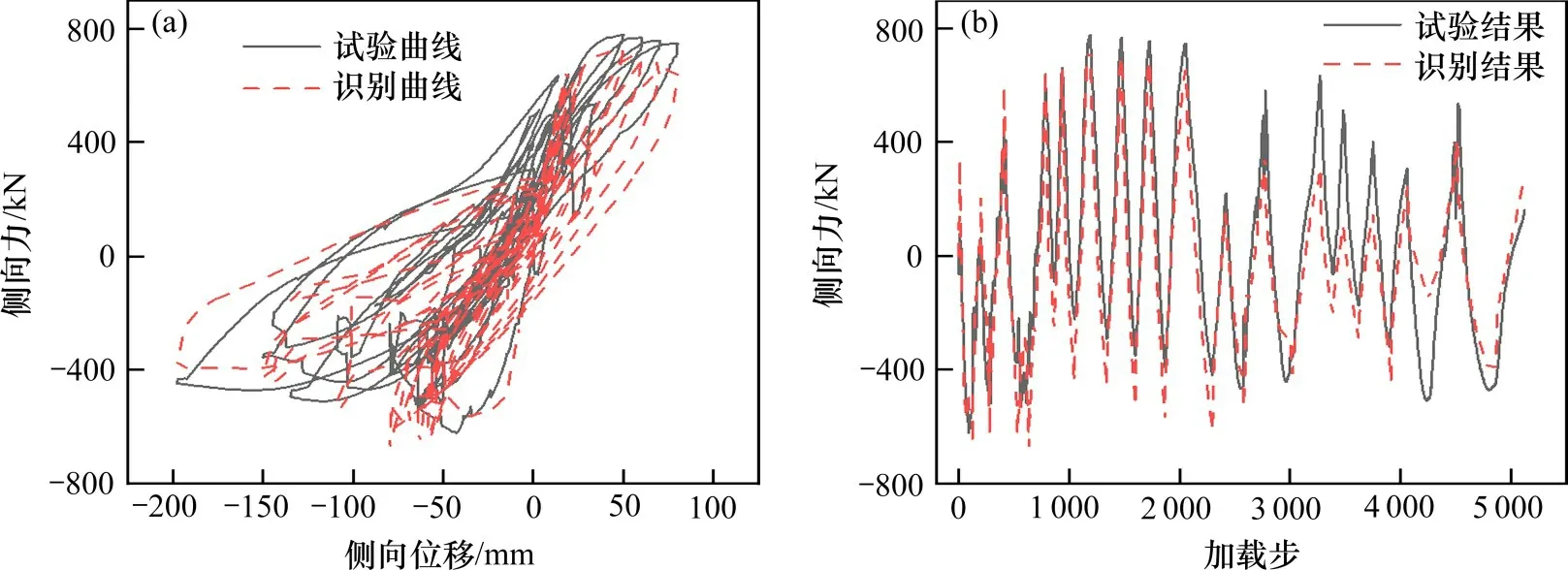
图5 变轴力柱识别结果Fig.5 Variable axial force column identification result

对变轴力柱识别数据与试验数据的相关性系数进行了计算，其值达到了0.893，按照数学上的定义可以认为2组数据为强相关。为了进一步确定改进模型对变轴力情况的适用性，对图6(a)框架输入Taft波作为水平和竖向双向地震波，对框架进行时程分析，并输出底层中柱轴力、位移和侧向力数据作为待识别的试验滞回曲线数据。识别的模型参数如表4 中C5 所示，对比结果如图6(b)和6(c)所示，识别的数据与纤维模型的计算数据相关性系数达到了0.952，说明识别结果良好，且改进的BWBN模型能用来描述变轴力柱的特性。

参考文献[21]离线模型更新混合试验方法，以C5 柱的识别结果为基础。使用El Centro 波作为水平及竖向地震波重新对图6(a)框架进行时程分析，获取底层中柱的侧向位移、侧向力及竖向力，用改进的BWBN 模型计算该加载路径下的侧向力，与时程分析的计算结果对比。重新加载的对比结果如图7所示，可以发现，对比结果良好。计算了对比数据的相关性系数，其值达到了0.945，说明改进的BWBN模型可以用于描述变轴力RC柱滞回特点,且对混合试验有一定借鉴意义。

图6 框架示意图及改进模型识别结果Fig.6 Framework diagram and improved model identification results

图7 El Centro波下纤维模型和改进BWBN模型计算结果对比Fig.7 Comparison of calculation results of fiber model and improved BWBN model under the El Centro wave

2.2.3 模型参数的影响

由于模型引入了新的参数，有必要重新对模型参数影响进行分析。结合参数识别经验，随机选取一组符合参考取值范围的参数作为基础模型参数：{β,γ,α0,n,δ'η,δ'υ,ζs,p,q,ψ,δψ,λ,r}={0.5, -0.4,0.2,2.5,0.05,0.02,0.1,1.2,5,1.8,0.14,0.5, -1.8}。如图8(a)所示，当刚度退化影响系数δ′η增大时，在弹性阶段由于构件累计损伤非常小，故而滞回曲线不受影响。但是当构件进入屈服时，由于累计损伤增加，滞回曲线的加载卸载刚度会相应减小，同时滞回面积减小，构件非线性滞回耗能能力下降。如图8(b)所示，当强度退化影响系数δ′υ增大时，每次加载循环滞回曲线的屈服强度不断减小。如图8(c)所示，形状参数n会影响滞回曲线的拐点，从而影响曲线形状。如图8(d)和8(e)所示，参数α0，r共同控制滞回曲线的屈服后刚度，其中α0越大，构件应变硬化现象越明显，r则降低了屈服后刚度。参数β，γ主要影响加卸载路径和每个滞回圈的极值。捏拢参数ζs越大，滞回曲线向平衡位置捏拢的现象越明显。单独改变p，q，ψ，δψ，λ的参数值并不能对滞回曲线造成很大的影响，这几个参数是与ζs共同作用来控制滞回曲线捏拢滑移的。这些参数影响与文献[6]接近，不再展示图片。

2.2.4 参数灵敏度分析

为研究不同模型参数对模型输出值的影响程度，对模型参数的灵敏度进行分析，基准参数值为{β,γ,α0,n,δ′η,δ′υ,ζs,p,q,ψ,δψ,λ,r}={0.9,-0.3,0.2,2.5,0.05,0.02,0.5,1.2,5,1.8,0.14,0.5,-1.8}。灵敏度确定方法为：将研究的参数在一定范围内变化，并保持其余参数不变，代入模型计算恢复力，并通过式(15)计算与基准模型的误差，并根据式(16)确定参数的灵敏度。灵敏度结果见图8(f)和表5。

表5 参数灵敏度排序及取值范围Table 5 Parameter sensitivity ranking and value range

图8 参数对恢复力模型的影响Fig.8 Influence of parameters on improved BWBN model

式中：Ei为参数第i次变化的模型误差值；Fj，F′j分别为第j步位移下基准和变化后模型的恢复力。

式中：Sm为参数m的灵敏度；M为参数m的变化次数。

根据图8(f)和表5 的计算结果，可以确定参数r，β，α0，ζs，n，γ，δ′η，δ′υ的灵敏度最高，其余参数影响较小，在进行在线或者离线的模型更新混合试验[21]时，可以只对这8 个参数进行更新，其余参数可以固定。此外，对peer 上的柱子数据以及变轴力柱试验数据和OpenSees 模拟的柱子双向地震下的数据进行参数识别，得到表5所示的模型参数的建议取值范围。

3 结论

1)基于16 根定轴力柱子的试验数据，对原始BWBN 模型进行了改进，改进后的模型相比原来能够更好地描述柱子的刚度、强度退化等滞回现象。

2) 将损伤指标引入BWBN 模型，并考虑正负向不对称损伤，对未来研究变轴力恢复力模型有一定借鉴意义。

3) 根据结论2 方法而提出的变轴力BWBN 模型能考虑轴力变化对柱子侧向滞回性能的影响，使得考虑轴力变化影响的柱模型更新混合试验成为可能。

4) 对改进模型参数敏感度进行了研究，发现参数r，β，α0，ζs，n，γ，δ′η，δ′υ的敏感度最高，故在实际应用时可以只识别这8个参数，其余参数保持不变。