正交异性钢桥面板纵肋-面板疲劳开裂的CFRP加固研究
徐伟伟,祝志文,2,牛华伟
(1. 湖南大学土木工程学院,湖南长沙 410082;2. 汕头大学土木与环境工程系,广东汕头 515063)
正交异性钢桥面板具有自重轻、承载能力高、适用范围广等突出优点,但其结构构造复杂,应力集中显著,在车辆轮载的作用下,疲劳开裂问题较为突出[1]。现有研究表明,RD 连接细节是钢桥面板中最容易发生疲劳开裂的构造细节之一[2]。RD 构造细节开裂会显著降低面板刚度,从而引起桥面铺装层脱黏和开裂。因此,对现役钢桥面板疲劳开裂的构造细节进行加固具有重要的工程实际意义。CFRP 是一种轻质高强的材料,具有优异的抗疲劳性能,在钢结构焊接构造细节疲劳加固应用方面具有显著优势[3-6]。WANG 等[5]对CFRP 加固波纹板焊接件进行了疲劳试验,结果表明CFRP加固能大幅提高焊接件的疲劳寿命。CHATAIGNER 等[6]采用CFRP 加固贾拉马桥对接焊缝并进行实桥加载,结果表明CFRP 加固可以使对接焊缝剩余疲劳寿命提高1 倍以上。因此,采用CFRP 加固RD 构造细节是很好的选择,但目前关于此方面研究还相对较少。XFEM是处理固体力学不连续问题的一种有效数值方法。采用XFEM 在模拟裂纹扩展时无需重新划分裂纹尖端网格,计算效率高,近年来在疲劳裂纹断裂分析中得到了广泛的应用[7-9]。在针对正交异性钢桥面板疲劳性能研究方面,王春生等[9]采用XFEM 模拟了正交异性钢桥面板各疲劳构造细节的裂纹并分析了其疲劳扩展特性。因此,本文借助有限元软件ABAQUS[10]建立正交异性钢桥面板单元数值模型,采用XFEM 模拟RD 构造细节的表面裂纹,分析CFRP 加固前后RD 构造细节的应力强度因子幅值以及应力的变化,进而探讨CFRP 加固正交异性钢桥面板RD 构造细节疲劳开裂的可行性。
1 疲劳裂纹模拟方法
1.1 扩展有限元方法
XFEM主要基于单元分解法,在常规有限元法中加入增强函数。增强函数由反映不连续性的阶跃函数和反映裂纹尖端奇异性的裂纹尖端渐近函数组成。基于单元分解法的位移渐进函数uXFEM(x)如式(1)所示:

其中:Ni(x)为节点i的标准形函数;ui为节点i的位移向量;H(x)为裂纹面阶跃函数;ai为H(x)对应增强自由度,γk(k=1,…,4)为裂纹尖端渐进函数;bik为γk对应的增强自由度;A为模型全部节点集;Ah为裂纹面贯穿节点集;Ac对应裂纹尖端的节点集。
H(x)能反映两侧位移的不连续性,在裂纹一侧等于1,另一侧等于-1,其表达式如式(2)所示:

1.2 应力强度因子解验证
在正交异性钢桥面板中,RD 构造细节处的裂纹面位移模式以I 型张开型为主[11],其表面裂纹一般为半椭圆裂纹[12],因此,本文主要验证XFEM 计算KI的准确性。在用XFEM 计算应力强度因子时,要考虑围道积分数的影响[10],则应力强度因子平均值KˉI计算公式如式(4)所示:
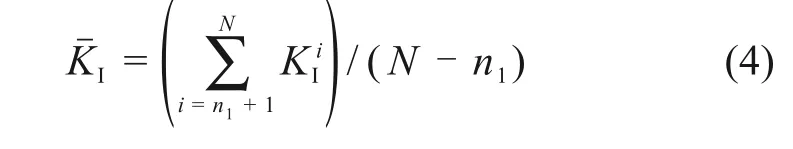
选取图2 含半椭圆表面裂纹的板,其中t=10 mm,b=20 mm,h=20 mm,材料为Q345qD,弹性模量E=206 GPa,两端施加σ=25 MPa 的均匀轴向拉应力,并取不同尺寸裂纹,如表1所示,计算不同N,n1条件下,A 点,B 点的KˉI值,并与对应的Newman-Raju应力强度因子解析解[13]比较。

表1 验证用裂纹尺寸Table 1 Crack size for verification
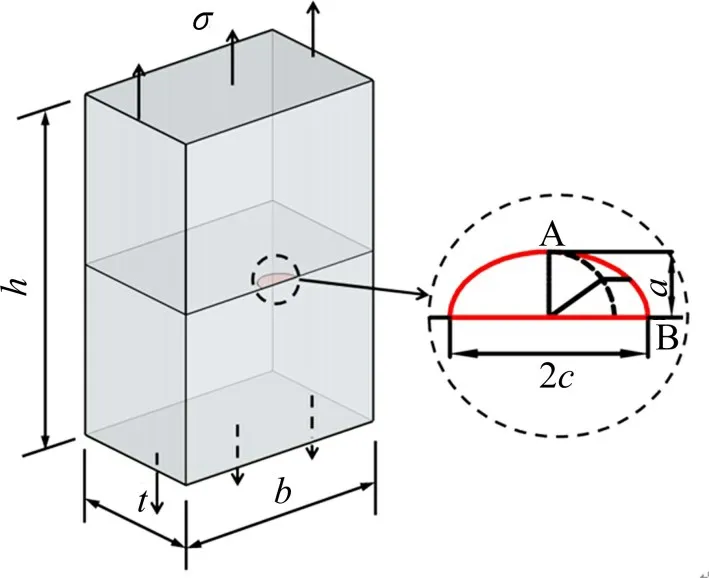
图2 验证模型Fig.2 Validation mode
根据式(6),计算裂纹A 点,B 点的KˉI值的δˉ,计算结果如表2 所示。从表2 可见,N=15,n1=2时,A 点和B 点的δˉ仅为3.61%,标准差最小仅为0.023 4,表明此时能够得到准确度高的计算结果。因此,在后续分析中取N=15,n1=2 进行应力强度因子计算。
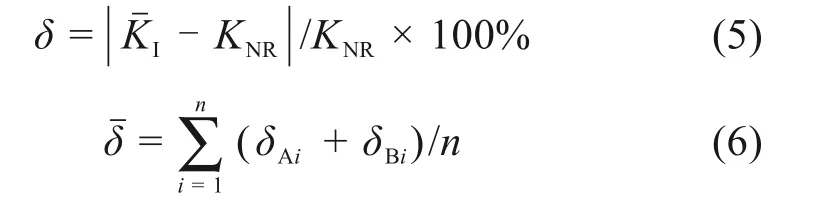

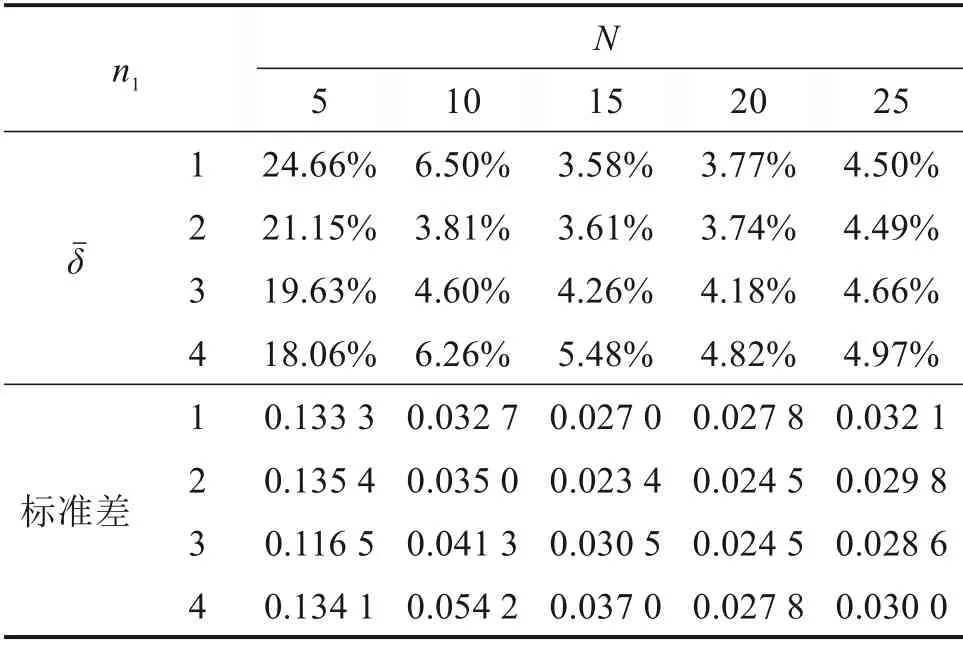
表2 不同N和n1条件下KˉI值误差Table 2 Error of KˉI under different N and n1 conditions
1.3 疲劳裂纹扩展速率
疲劳裂纹扩展速率da/dN与应力强度因子幅值ΔK的关系式为:
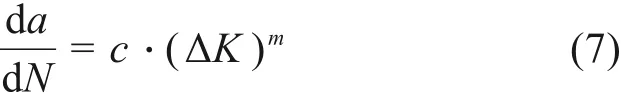
其中:c和m为描述材料疲劳裂纹扩展性能参数。式(7)表明ΔK为疲劳裂纹扩展速率主要控制变量。
残余拉应力会改变应力比,应力比对焊接结构的疲劳裂纹扩展速率影响小[14]。OHTA 等[15]的研究也表明对焊接构造,ΔK是最重要的影响因素,应力比影响小。并且,目前关于RD 构造细节残余应力的主要研究对其量值和分布的认识仍不统一,且疲劳裂纹扩展过程中裂纹局部区域残余应力将重分布并逐渐释放[16]。因此,为较为合理地研究CFRP 加固RD 构造细节的效果,在后续的有限元分析中,不考虑残余应力的影响。
2 CFRP加固RD构造细节
以某大跨度双塔双索面混合梁斜拉桥为工程背景,主桥主跨采用PK 断面钢箱梁,钢材为Q345qD。桥面结构采用正交异性钢桥面板,桥面板厚16 mm,U 肋厚8 mm,上口宽300 mm,下口宽180 mm,中心间距为600 mm,U 肋典型构造细节如图3所示。
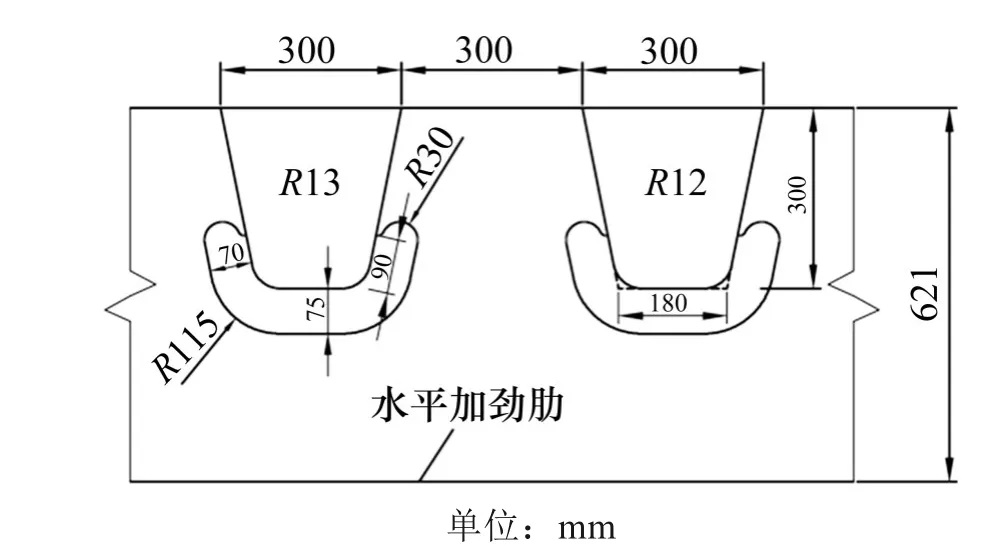
图3 正交异性钢桥面板构造细节Fig.3 Structural details of orthotropic steel bridge deck
2.1 CFRP加固方案
本文加固对象为位于两横隔板间纵肋跨中处,含面板侧焊趾表面裂纹的RD 构造细节,图4所示。

图4 RD构造细节Fig.4 RD welding detail
基于CHEN 等[4-5]对焊接件CFRP 加固研究,本文采用CFRP 加固RD 构造细节方案如图5 所示,CFRP 层数为1~9 层,CFRP 纵向长度D和面板、纵肋侧宽度Bd,Br与实际构件相协调[3]。
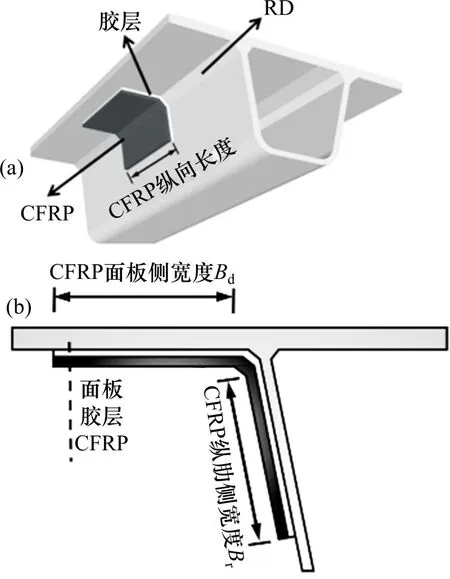
图5 CFRP加固RD构造细节Fig.5 RD welding detail reinforced with CFRP
本文采用CFRP 布加固,能适应不平整的焊缝[17],并选用高弹模CFRP 布[4]。CFRP 弹性模量为435 GPa,厚度为0.163 mm,抗拉强度为4 710 MPa,结构胶弹性模量为2.9 GPa,厚度为0.4 mm[18],CFRP,结构胶以及钢材的本构关系均为线弹性[5,19-21]。
现有研究表明,每层CFRP 布的承担应力比例均不一样[22],以CFRP 等效前后受力不变为前提条件,可将多层CFRP 等效为一层CFRP,保守计算时只考虑CFRP 不考虑胶层刚度贡献[18],只记CFRP 厚度并且厚度不变,等效弹性模量按式(8)计算。
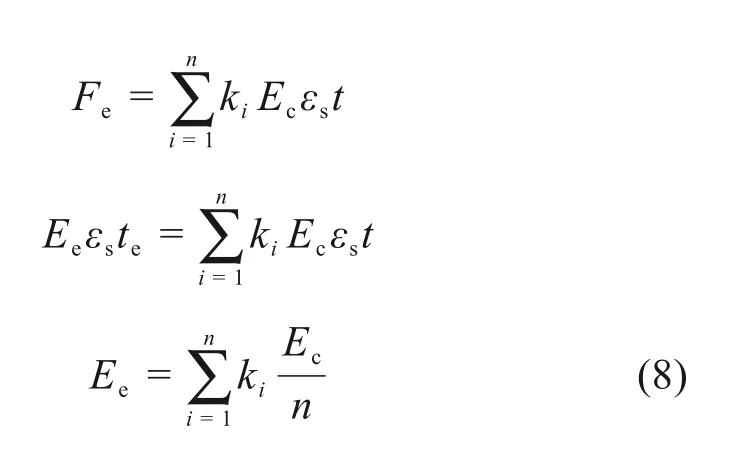
te为等效后CFRP厚度,t为单层CFRP厚度,te=nt,Fe为多层CFRP 合力,Ee为等效CFRP 弹性模量,Ec为CFRP弹性模量,εs为钢板应变,等效时,假设CFRP 与钢板之间存在良好的黏结,CFRP 应变等于钢板应变εs,ki为折减系数,k1=1.0,k2=0.78,当层数大于等于3 时,k=0.56,n为CFRP层数。
胡黎俐等[18,22]将多层CFRP 等效为单层CFRP进行计算,并与试验结果对比分析,结果表明等效方法是合理的。
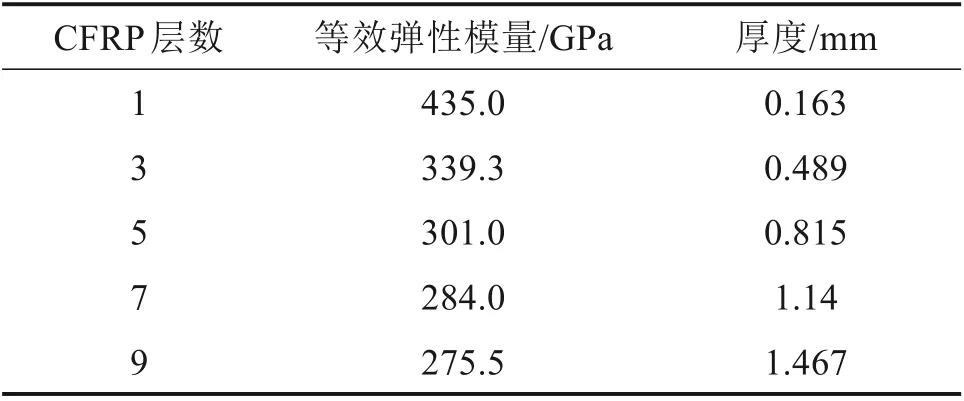
表3 多层CFRP等效材料特性Table 3 Equivalent characteristics of multilayer CFRP
2.2 有限元模型
本文借助有限元分析软件ABAQUS,建立多尺度数值模型,根据正交异性钢桥面板应力局部效应特征[23],取横桥向5个U 肋宽度(3 m),纵桥向3 个横隔板(12 m)组成4 跨正交异性钢桥面板节段作为计算模型,约束横隔板底部X和Z方向平动位移,约束钢桥面板端部Y和Z方向平动位移以及绕X和Z轴的转动,约束钢桥面板纵向两侧X方向平动位移以及绕Y和Z轴的转动[24],具体如图6所示。
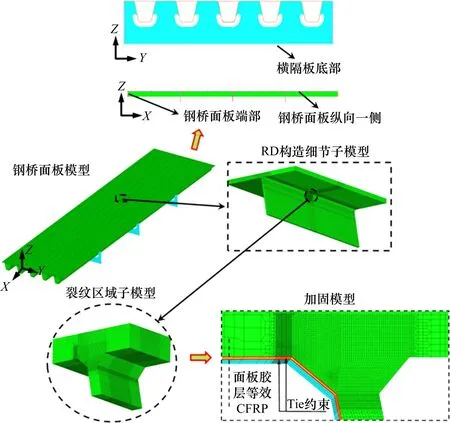
图6 多尺度模型Fig.6 Multi-scale model
图6 中,钢桥面板节段模型与RD 构造细节子模型接触采用壳固耦合(shell-to-solid coupled),其中钢桥面板节段模型采用S4R 壳单元,RD 构造细节子模型采用C3D8R 实体单元。本文采用XFEM模拟裂纹,裂纹区域子模型实体单元采用0.2 mm C3D8 实体单元单元精细划分,根据JOHN 等[25]的研究,当a/t≤0.5 时,T 型焊接件焊趾处疲劳裂纹c/a的值将趋于2.9,且扩展过程中可能出现任意形状半椭圆裂纹,为较为合理地体现CFRP 加固的效果,分别模拟c/a=2,4,6等形状的裂纹。
本文中CFRP 和胶层均采用C3D8 实体单元模拟[23],胶层与RD 构造细节、CFRP 的接触均采用Tie 约束,不考虑黏结滑移,加固模型示意如图6所示,图中加固模型从上到下,依次为面板(深色单元)、胶层(浅色单元)和CFRP(深色单元)。CFRP 加固模型单元数量为1 287 668,节点数为1 266 814。
本文开展CFRP 加固模拟方法的计算验证,结果表明采用Tie 约束进行加固模拟,不考虑黏结滑移的方法是合理可靠的,与一些学者研究结论较为一致[4-5,19-21]。
2.3 疲劳加载
根据《公路钢结构桥梁设计规范》(JTG D64—2015)[14],采用疲劳荷载模型Ⅲ。分析中只考虑横向一侧车轮一个双联轴的加载[24],其中双联轴轴距为1.2 m,单轴荷载为120 kN,轮胎尺寸为0.2 m×0.6 m。轮胎横向尺寸考虑桥面铺装的影响,按45 度角扩散:沥青铺装层为0.07 m,则单个轮胎在钢面板上的加载尺寸为0.34 m×0.74 m。
车载横向布置选取最不利加载位置跨肋式[23],即横桥向轮载中心位于纵肋腹板正上方的位置,如图7(a)所示。车载在桥面上的移动通过Fortran编写的子程序UTRACLOAD 来实现,车载在每个计算步移动0.1 m,移动加载以后轮驶出最右横隔板为结束标志,如图7(b)所示,此时加载步数N=102。
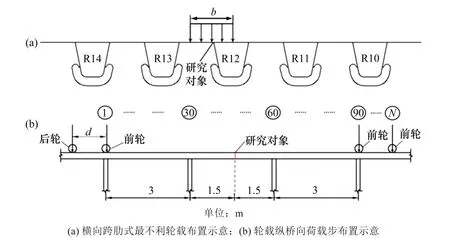
图7 轮载布置Fig.7 Layout of wheel loading
3 计算结果与分析
3.1 加固前后ΔKI对比分析
图8(a)和8(d)所示为加固前裂纹A 点和B 点的ΔKI,其中,疲劳裂纹扩展的应力强度因子门槛值ΔKth根据日本JSSC 规范[26]取为92 MPa·mm1/2。图8(a)和8(d)中,c/a=2,4,6 时,在疲劳荷载作用下RD 构造细节ΔKI均明显大于门槛值ΔKth,说明RD构造细节焊趾处大多数裂纹均会不断扩展,而且随着裂纹增长,裂纹B 点ΔKI值越大,即表面裂纹扩展速率越快。
为定量评价CFRP 加固效果,以加固前后ΔKI降幅ηΔKI作为评价参数,降幅ηΔKI按式(9)计算。
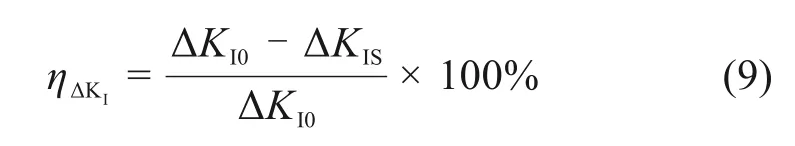
其中:ΔKI0,ΔKIS分别为加固前、后的应力强度因子幅值。图8(b)~8(c)、8(e)~8(f)为CFRP 加固后裂纹A 点和B 点的ΔKI以及ηΔKI值。图8 中ΔKIa,ΔKIb分别表示裂纹A 点和B 点的ΔKI。具体加固参数:D=150 mm,Bd=Br=60 mm,厚度为0.815 mm,胶层厚度为0.4 mm。
图8(b)~8(c)中,对于任意深度裂纹,CFRP加固均能显著降低其ΔKIa,降幅ηΔKI在31.20%~78.26%,并且随着裂纹深度的增加,ηΔKI不断增大。
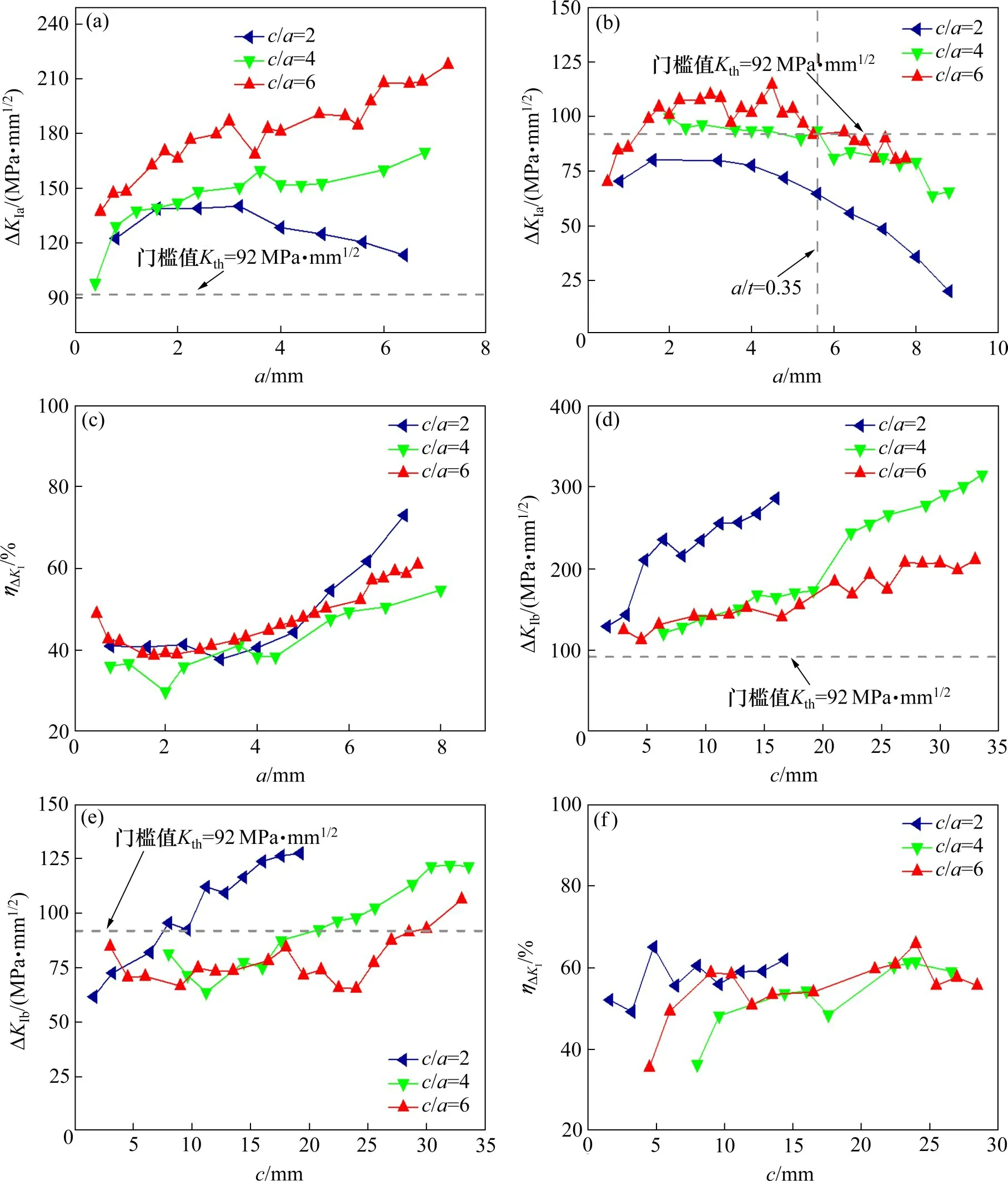
图8 CFRP加固前后ΔKI以及ηΔKI值Fig.8 ΔKI and ηΔKIbefore and after RD welding detail reinfoced with CFRP
当a/t≥0.35,c/a=2,4,6 时,ΔKIa均小于门槛值ΔKth,即疲劳裂纹停止向裂纹深度方向扩展。根据IIW[27],a/t=0.5 时,该构造失效,因此,CFRP加固能使焊趾处开裂的RD 构造细节达到无限寿命。
为安全估计CFRP 加固的具体效果,假定加固后,a/t≥0.35 时,疲劳裂纹仍能扩展,以式(10)~(12)计算疲劳寿命增长倍数RN。


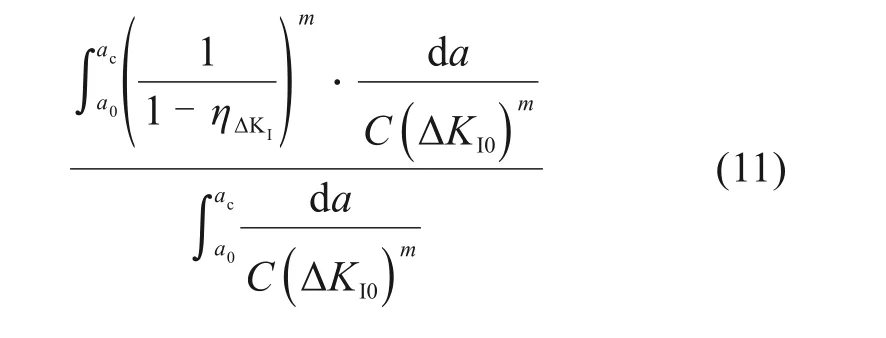
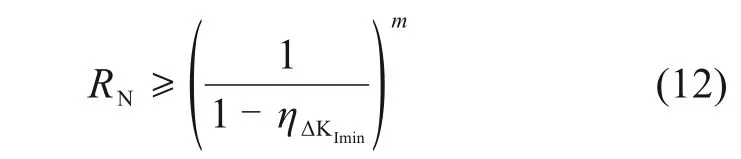
其中:a0,ac分别表示初始裂纹尺寸、临界裂纹尺寸;Ns,N0分别表示为加固、未加固的疲劳寿命,ηΔKImin表示ΔKI降幅最小值。上式解得加固后疲劳寿命Ns至少为未加固疲劳寿命N0的3.7倍。
从图8(e)~8(f)中可以看出,当裂纹尺寸c/t<0.3n,n=c/a时,CFRP 加固能阻止裂纹沿表面扩展,但是随着裂纹尺寸的增加,ΔKIb会超过门槛值ΔKth,主要因为随着裂纹尺寸增长,ΔKIb增幅过大,如c/a=4,c从14.4 mm 增至30.40 mm 时,CFRP 加固前ΔKIb从167.71 MPa·mm1/2增至290.96 MPa·mm1/2,CFRP 加固后ΔKIb从77.55 MPa·mm1/2增至121.61 MPa·mm1/2,ΔKIb降幅ηΔKI均在55%左右,但由于ΔKIb增加过快,CFRP 已不足以完全限制裂纹B 点的扩展。从图8(f)也可以发现,当c/t≥0.1n,n=c/a时,裂纹B 点ηΔKI将稳定在50%~60%之间,说明随着裂纹尺寸增长,CFRP 仍能保证一定的加固效果。
上述结果表明,CFRP 加固能有效降低RD 构造细节焊趾处疲劳裂纹扩展速率,增加其疲劳寿命。
3.2 加固前后应力对比分析
为了有效分析CFRP 加固具体效果,取轮载中心位于两横隔板间U 肋跨中时,加固前后应力云图,如图9 所示,其中D=150 mm,Bd=Br=60 mm,厚度为0.815 mm,胶层厚度为0.4 mm,裂纹尺寸a=6.4 mm,c=12.8 mm。
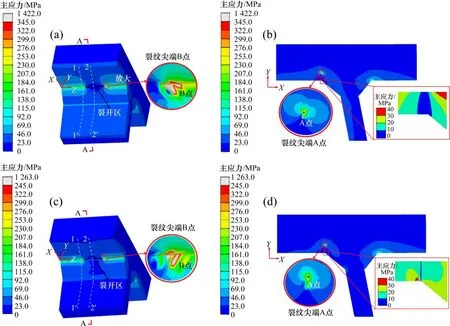
图9 应力比较Fig.9 Comparison of stress
图9 中,CFRP 加固前后裂纹附近均有小部分区域最大主应力大于钢材屈服强度345 MPa,主要是因为本文模型是基于线弹性断裂力学建立的,靠近裂纹尖端理论上是无穷大[28]。为更好分析CFRP 具体加固机理,取远离裂纹尖端的路径1-1′以及2-2′的主应力分布,如图10 所示。在图9 和图10(a)中,CFRP加固前,应力主要集中在裂纹尖端附近;CFRP 加固后,应力发生重分布,裂纹A点和B点以及焊趾应力集中现象明显减弱,总体上应力出现明显降幅,沿路径1-1′分布应力平均降幅达23.9%,最大主应力从224.76 MPa 下降至173.40 MPa,说明CFRP 加固降低了焊趾附近的应力水平。
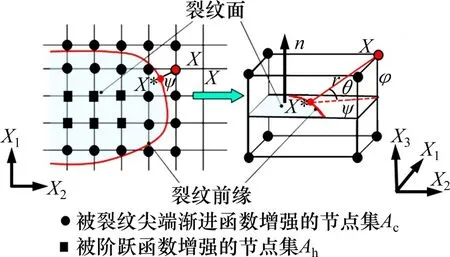
图1 扩展有限元法中的增强节点Fig.1 Enriched nodes in XFEM
在图9 和图10(b)中,CFRP 加固前,路径2-2′裂开区(构造细节开裂产生的不连续界面)焊趾表面基本不受力,在0~5 MPa 左右;CFRP 加固后,路径2-2′裂开区焊趾处主应力增至40 MPa 左右,说明CFRP 限制了裂开区的变形。而且图10(b)中除裂开区焊趾处之外,沿路径2-2′分布的应力明显降低,峰值降幅达38.9%,说明CFRP 加固一方面降低RD 构造细节焊趾附近的应力集中程度,另一方面限制裂开区变形,增强RD 构造细节裂开区的连接效应。
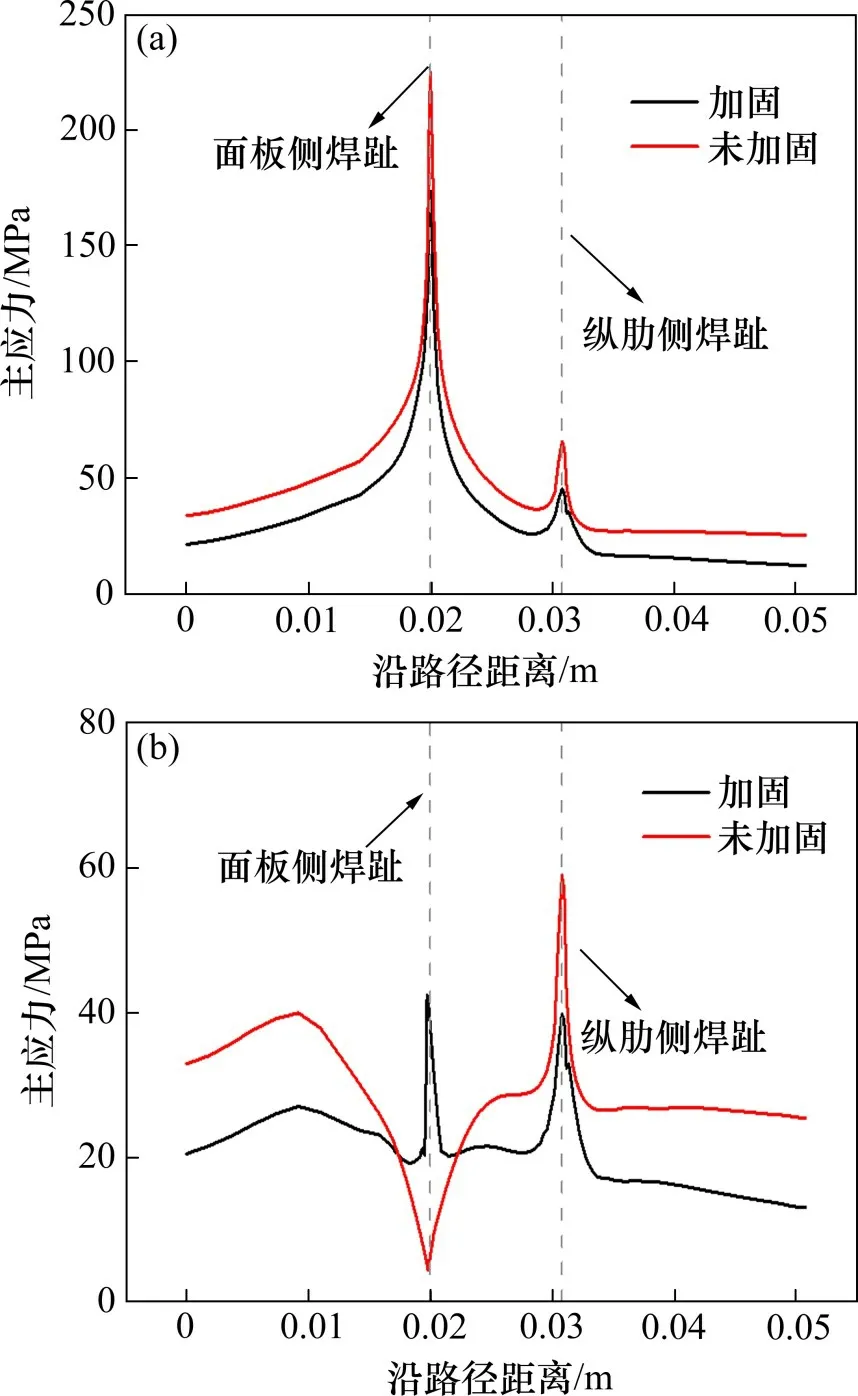
图10 沿路径主应力Fig.10 Principle stress along path
3.3 加固参数分析
3.3.1 CFRP层数
CFRP 的层数作为加固过程中的重要参数,直接影响具体的加固效果,因此以CFRP 层数为变量,控制D=150 mm,Bd=Br=60 mm,胶层厚度为0.4 mm,裂纹形状c/a=2,分析CFRP 层数对加固效果的影响。为有效评价CFRP 不同层数加固效果的差异,以1 层CFRP 加固后ΔKIa为基准,计算其余层数相对1 层CFRPΔKIa降幅ηLavers,按式(13)计算,结果如图11(a)所示。
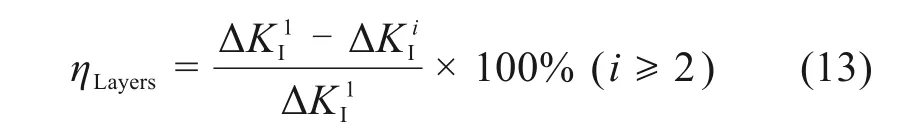
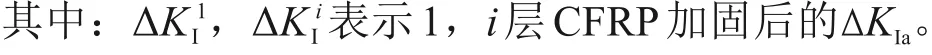
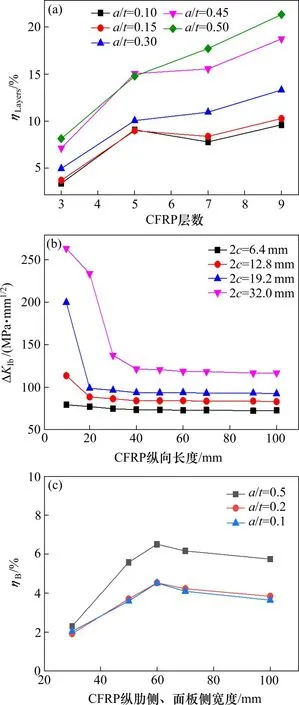
图11 CFRP加固参数分析Fig.11 Parameter analysis of CFRP reinforcement
由图11(a)可知,随着CFRP 层数的增加,ηLavers越大,说明加固效果越好,可能是因为随着CFRP厚度的增加,CFRP 对裂开区变形的限制作用就越大。由图11(a)可以发现,当CFRP层数为5时,ηLa-vers出现转折,后续增长变缓,如a/t=0.3 时,当CFRP 层数从1 层增至5 层时,ηLavers为10.03%;当CFRP 层数从5 层增至9 层时,ηLavers为13.29%,说明CFRP 层数取5 时,再增加CFRP 层数,对加固效果增幅较小。
3.3.2 CFRP纵向长度D
CFRP 纵向长度与加固效果直接相关,是加固过程中的重要参数,以CFRP 纵向长度为变量,控制CFRP 厚度为0.815 mm,Bd=Br=60 mm,胶层厚度为0.4 mm,分析CFRP纵向长度对加固效果的影响,计算结果如图11(b)所示。
由图11(b)可知,当CFRP 纵向长度小于2c时,随着CFRP 纵向长度增加,ΔKIb越小,当CFRP 纵向长度大于2c时,ΔKIb随CFRP 纵向长度变化的幅度很小,表明CFRP 覆盖住裂纹时,再增加CFRP纵向长度对加固效果影响很小,可能是因为当裂纹被CFRP 完全覆盖之后,CFRP 对焊趾裂开区的连接效应以及减缓应力集中的作用接近峰值。
3.3.3 CFRP纵肋、面板侧宽度Bd,Br
为了解Bd,Br对CFRP 加固效果的影响,令Bd=Br=B,以B为变量,控制D=150 mm,厚度为0.815 mm,胶层厚度为0.4 mm,同3.3.1 节,为有效评价CFRP 不同层数加固效果的差异,以B=20 mm 时的CFRP 加固后ΔKIb为基准,计算B相对B=20 mm 时的CFRP 加固后ΔKIb降幅ηB,按式(14)计算,结果如图11(c)所示。

由图11(c)可知,随着CFRP面板、纵肋侧宽度增大,ΔKIb越小,但是当B大于60 mm 时,变化明显变缓,可能是因为CFRP 宽度到达某个值时,RD 构造细节已经能通过胶层有效传力至CFRP,再增大CFRP 宽度并不能有效改善局部细节处的受力。
4 结论
1)采用CFRP 加固RD 构造细节方法对大多数裂纹效果明显,能有效降低裂纹疲劳扩展速率,其疲劳寿命至少增至未加固时的3.7倍。
2) CFRP 加固后,总体上应力出现明显降幅,应力平均降幅在23.9%~38.9%,RD 构造细节裂开区附近主应力从0~5 MPa增至40 MPa左右,说明CFRP 加固一方面降低了焊趾附近的应力集中程度,另一方面增强了RD构造细节裂开区的连接。
3)CFRP加固效果随着CFRP层数、纵向长度、面板侧以及纵肋侧宽度的增加而提高,但若CFRP层大于5 时,其加固效果增幅不明显,对本文的CFRP 纵向长度、宽度、胶层厚度,建议实际加固中使用5层CFRP。
4)CFRP 纵向长度以及面板、纵肋侧宽度均存在加固最优尺寸,即CFRP 纵向长度或面板侧以及纵肋侧宽度大于某一值时,再增加尺寸对加固效果影响很小。对本文研究对象,CFRP 纵向长度加固较优尺寸为封闭裂纹时的尺寸,CFRP 面板、纵肋侧宽度较优尺寸为60 mm。

